智科人之人工智能课程上机实验(智科还单独有一个综合实验):PROLOG语言练习与编程上机实验
各个专业的prolog需要掌握的程度都是不一样的,实验要求也不一样:
智科牛马的在此:(好像占平时成绩20分还是多少来的)
其他专业只有一个课程设计实验,我们这个有一个综合实验和一个课上编程实验,而且期末考试最后一道大题会有编程题,十几分好像,所以这个语言的基本还是掌握一点比较好:
相关程序我放在资料区(免费下载),资源文件夹:人工智能之prolog程序参考
文件内容:
报告开始
一.判断是不是表的成员
member(X, [X | Tail]).
member(X, [Head | Tail]) :- member(X, Tail).
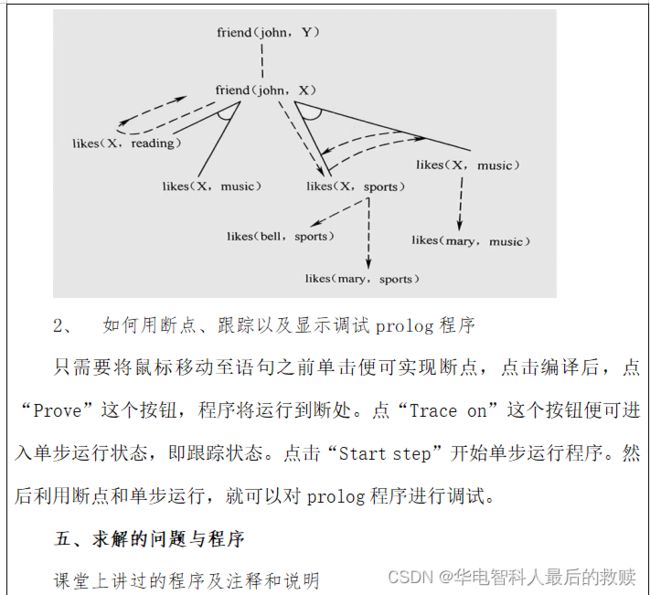
其中第一个子句的语义就是上面的第一句话;第二个子句的语义就是上面的第二句话。可以看出,这个程序中使用了递归技术,因为谓词 member 的定义中又含有它自身。利用这个程序就可以判定任意给定的一个对象和一个表之间是否具有 member(成员)关系。
member(3,[1,2,3]) 判断3是否在表[1,2,3]中
member(X,[X|_]). 如果X与L的表头是同一个对象,则X是L的成员
member(X,[_|T]):-如果X是L的表尾的成员,则X是L的成员
member(X,T).
二.表的拼接程序,即把两个表连接成一个表
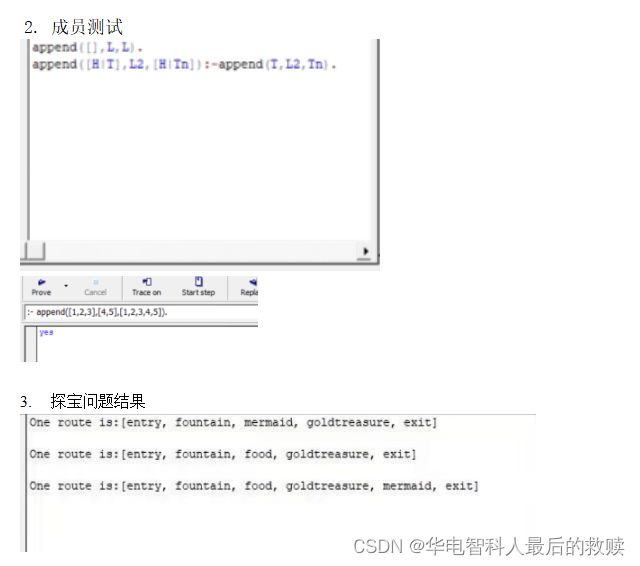
append([],L,L).
append([H|T],L2,[H|Tn]):-append(T,L2,Tn).
输入:?-append([1,2,3],[4,5],[1,2,3,4,5]). 输出: yes
输入:?-append([1,2,3],[4,5],[1,2,3,4,5,6]). 输出:no
三.探宝问题
目标: go(entry,exit).
go(Start,Goal):-
route(Start,Goal,[Start],VisitedL),
reverse(VisitedL,[],RVisitedL),
write("One route is:"),
write(RVisitedL),nl,nl,
fail.
go(_,_).
neighbor(X,Y):-gallery(X,Y).
neighbor(X,Y):- gallery(Y,X).
avoid([monsters,hell,robbers]). %规避必要因素
gallery(entry,fountain). %定义廊道
gallery(entry,monsters).
gallery(monsters,goldtreasure).
gallery(goldtreasure,food).
gallery(food,fountain).
gallery(goldtreasure,robbers).
gallery(goldtreasure,exit).
gallery(fountain,mermaid).
gallery(fountain,robbers).
gallery(mermaid,exit).
gallery(hell,fountain).
gallery(mermaid,goldtreasure).
reverse([],Y,Y).
reverse([H|T],R0,R):-
reverse(T,[H|R0],R).
member(X,[X|_]).
member(X,[_|T]):-
member(X,T).
route(Room,Room,VisitedL,VisitedL):-
member(goldtreasure,VisitedL),!.
route(Room,WayOut,VisitedL0,VisitedL):-
neighbor(Room,NextRoom),
avoid(DangousL),
not(member(NextRoom,DangousL)),
not(member(NextRoom,VisitedL0)),
route(NextRoom,WayOut,[NextRoom|VisitedL0],VisitedL).
四.Hanoi塔问题
问题框:- hanoi(4).
hanoi(N):-
move(N,left,middle,right),nl,nl.
move(1,A,_,C):- %如果盘片号是1,则直接将盘片从A移到C
inform(1,A,C),!.
move(N,A,B,C):- %借助B柱,把N片从A柱移动到C柱上
N1 is N-1,
move(N1,A,C,B), %借助C柱,把N1片从A柱移动到B柱上
inform(N,A,C), %告知将第N片从A移到C
move(N1,B,A,C). %借助A柱,把N1片从B柱移动到C柱上
inform(N,Loc1,Loc2):-
writelist(['Move disk', N, 'from', Loc1, 'to', Loc2]), nl.
writelist([]).
writelist([H|T]):-
write(H), write(' '),
writelist(T).
五.单词交叉排列问题
目标: crosswd(V1,V3,V3,H1,H2,H3).
word(abalone,a,b,a,l,o,n,e). %定义单词
word(abandon,a,b,a,n,d,o,n).
word(enhance,e,n,h,a,n,c,e).
word(anagram,a,n,a,g,r,a,m).
word(connect,c,o,n,n,e,c,t).
word(elegant,e,l,e,g,a,n,t).
crosswd(V1,V2,V3,H1,H2,H3):- %定义顺序
word(V1,_,A,_,B,_,C,_),
word(V2,_,D,_,E,_,F,_),
word(V3,_,G,_,H,_,I,_),
word(H1,_,A,_,D,_,G,_),
word(H2,_,B,_,E,_,H,_),
word(H3,_,C,_,F,_,I,_).
go(Queens):-
template(Queens),
solutions(Queens),
write('one solution is '), nl,
write(Queens),nl,
fail.
go(_).
template([1/Y1,2/Y2,3/Y3,4/Y4,5/Y5,6/Y6,7/Y7,8/Y8]).
% 这里假设8个皇后在棋盘上从第1列到第8列依次排放(X=1~8)
求它们应在Y轴上对应的行号,以躲开其他皇后的攻击
solutions([]).
solutions([X/Y|Others]):-
solutions(Others),
member(Y,[1,2,3,4,5,6,7,8]),
noattack(X/Y,Others).
noattack(_,[]).
noattack(X/Y,[X1/Y1|Rest]):-not(Y=Y1),
Y =\= Y1,
Y1 - Y =\= X1 - X,
Y1 - Y =\= X - X1,
noattack(X/Y,Rest).
member(X,[X|_]).
member(X,[_|T]):-
member(X,T).
七.传教士和野人问题
问题框::- solve([3,3,near],[0,0,far]).
主代码:% start([3,3,near]).
% goal([0,0,far]).
change(near,far).
change(far,near).
% boat must be in valid location
% valid number of missionaries and cannibals on each shore
% no more than three and no fewer than zero
valid([Missionaries,Cannibals,near]) :-
Missionaries=<3,
Cannibals=<3,
Missionaries>=0,
Cannibals>=0.
valid([Missionaries,Cannibals,far]) :-
Missionaries=<3,
Cannibals=<3,
Missionaries>=0,
Cannibals>=0.
% oneEq(X,X,_).
% oneEq(X,_,X).
% no missionaries are in danger of being eaten
safe([Missionaries,Cannibals,_]) :-
% oneEq(3,3,_),oneEq(2,2,_),oneEq(1,1,_),oneEq(0,0,_),oneEq(0,1,_),
oneEq(0,2,_),oneEq(0,3,_),oneEq(3,0,_),oneEq(3,1,_),oneEq(3,2,_).
% (Missionaries==Cannibals ; Missionaries=0),
FarMis is 3 - Missionaries, FarCan is 3 - Cannibals,
(FarMis >= FarCan; FarMis=0),!.
%twocannibal
move([Missionaries1,Cannibals1,Boat1],twocannibals,
[Missionaries2,Cannibals2,Boat2]) :-
change(Boat1, Boat2),
Missionaries1 = Missionaries2,
(Boat1=near -> DummyCannibal is Cannibals1-2;
DummyCannibal is Cannibals1+2),
Cannibals2 = DummyCannibal.
%onecannibal
move([Missionaries1,Cannibals1,Boat1],onecannibal,
[Missionaries2,Cannibals2,Boat2]) :-
% boat1==near,boat2==far,Cannibals2 is Cannibals1 - 1;
% boat1==far,boat2==near,Cannibals2 is Cannibals1 + 1.
change(Boat1,Boat2),
Missionaries1 = Missionaries2,
(Boat1=near -> DummyCannibal is Cannibals1-1 ;
DummyCannibal is Cannibals1+1),
Cannibals2 = DummyCannibal.
%twomissionaries
move([Missionaries1,Cannibals1,Boat1],twomissionaries,
[Missionaries2,Cannibals2,Boat2]) :-
change(Boat1,Boat2),
Cannibals1 = Cannibals2,
(Boat1=near -> DummyMissionary is Missionaries1-2 ;
DummyMissionary is Missionaries1+2),
Missionaries2 = DummyMissionary.
% onemissionary
move([M1,C1,B1],onemissionary,[M2,C2,B2]) :-
change(B1, B2),
C1 = C2,
(B1=near -> DM is M1-1 ; DM is M1+1),
M2 = DM.
% oneofeach
move([Missionaries1,Cannibals1,Boat1],oneofeach,
[Missionaries2,Cannibals2,Boat2]) :-
change(Boat1,Boat2),
(Boat1=near -> DummyCannibal is Cannibals1-1,
DummyMissionary is Missionaries1-1 ; DummyCannibal is Cannibals1+1,
DummyMissionary is Missionaries1+1),
Cannibals2 = DummyCannibal,
Missionaries2 = DummyMissionary.
/*
solution([0,0,far],[]):-!.
solution(State,[Move|Rest]) :-
move(State,Move,NextState),
valid(NextState),
write('NextState='),nl,
safe(NextState),
write(' Safe NextState='),nl,!,
write(NextState),nl,!,
solution(NextState,Rest).
*/
solution([0,0,far],Closed,Closed,MoveL,MoveL):-!.
solution(State,Closed0,Closed,MoveL0, MoveL) :-
move(State,Move,NextState),
valid(NextState),
not(member(NextState,Closed0)),
write('NextState='),nl,
safe(NextState),
write(' Safe NextState='),nl,!,
write(NextState),nl,!,
solution(NextState,[State|Closed0],Closed,[Move|MoveL0], MoveL).
member(X,[X|_]):-!.
member(X,[_|T]):-member(X,T).
solve(StateL,MoveL) :-
% length(X,11),
solution([3,3,near],[],StateR,[],MoveR),!,
reverse([[0,0,far]|StateR],[],StateL), reverse(MoveR,[],MoveL),
write("One solution-States"),write(StateL),nl,
write("One solution-Moves"),write(MoveL),nl,
!.
reverse([],Y,Y).
reverse([H|T],R0,R):-
reverse(T,[H|R0],R).
writelist([]):-nl,nl.
writelist([H|T]):-
write(H), write(' '),
writelist(T).
nomember(X,[]).
nomember(X,[X|_]):-!,fail.
nomember(X,[_|T]):-
nomember(X,T).
六、讨论与结论
通过这次实验,我对“Prolog(语言是一种基于 [Horn 子句]的逻辑型程序设计语言,也是一种陈述性语言。 Prolog 与人工智能的知识表示、自动推理、图搜索、产生式系统和专家(知识)系统有着天然的联系,非常适合智能程序设计。”的概念性理解更加深刻,prolog和我们其他学过的高级语言不一样,它更适合与逻辑推理,也就是能把一些算法变的更加简单理解,更容易实现。
而Prolog语言的求解过程更是通过规则来匹配的过程,实验室的trinc prolog的编程环境,操作方式、prolog语言的回溯、递归技术,对我来说都是一次全新的学习,让我收益匪浅。
老师的ppt和课本的概念性知识,还有百度的介绍以及CSDN的prolog程序详细解答,都给我这次学习提供了很大的帮助,特别是当我头痛这个语言的理解和繁琐时(误以为),在重新静下心来好好理解和看概念,才感觉豁然开朗。
最重要的是调试和输入问题框时候,prolog语言的输入形式一定要要严格遵守,“:-”“.”少打都会出现脚本报错。
最后的大实验更是上升一些难度,多亏了实验室身边的同学耐心的指导,才有了今天的成果,非常感谢智科的同学们,感谢这个温暖的大家庭,这个团结合作的平台,也感谢热心的老师的耐心指导和代码文件的传送,谢谢你们XXXXXXXXXXXXXXXXXXXXX(瞎编)
谢谢你,因为有你,温暖了四季。。。。。。
七、所附实验输出的结果或数据
运行结果(有些没截图,但是有U盘保存的结果,所以大家记得截图,实验报告好有点东西)
1.汉诺塔问题
Move disk 1 from left to middle
Move disk 2 from left to right
Move disk 1 from middle to right
Move disk 3 from left to middle
Move disk 1 from right to left
Move disk 2 from right to middle
Move disk 1 from left to middle
Move disk 4 from left to right
Move disk 1 from middle to right
Move disk 2 from middle to left
Move disk 1 from right to left
Move disk 3 from middle to right
Move disk 1 from left to middle
Move disk 2 from left to right
Move disk 1 from middle to right

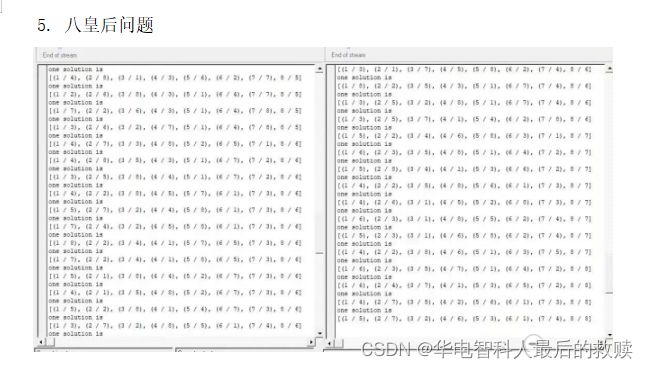
one solution is
[(1 / 4), (2 / 2), (3 / 7), (4 / 3), (5 / 6), (6 / 8), (7 / 5), 8 / 1]
one solution is
[(1 / 5), (2 / 2), (3 / 4), (4 / 7), (5 / 3), (6 / 8), (7 / 6), 8 / 1]
one solution is
[(1 / 3), (2 / 5), (3 / 2), (4 / 8), (5 / 6), (6 / 4), (7 / 7), 8 / 1]
one solution is
[(1 / 3), (2 / 6), (3 / 4), (4 / 2), (5 / 8), (6 / 5), (7 / 7), 8 / 1]
one solution is
[(1 / 5), (2 / 7), (3 / 1), (4 / 3), (5 / 8), (6 / 6), (7 / 4), 8 / 2]
one solution is
[(1 / 4), (2 / 6), (3 / 8), (4 / 3), (5 / 1), (6 / 7), (7 / 5), 8 / 2]
one solution is
[(1 / 3), (2 / 6), (3 / 8), (4 / 1), (5 / 4), (6 / 7), (7 / 5), 8 / 2]
one solution is
[(1 / 5), (2 / 3), (3 / 8), (4 / 4), (5 / 7), (6 / 1), (7 / 6), 8 / 2]
one solution is
[(1 / 5), (2 / 7), (3 / 4), (4 / 1), (5 / 3), (6 / 8), (7 / 6), 8 / 2]
one solution is
[(1 / 4), (2 / 1), (3 / 5), (4 / 8), (5 / 6), (6 / 3), (7 / 7), 8 / 2]
one solution is
[(1 / 3), (2 / 6), (3 / 4), (4 / 1), (5 / 8), (6 / 5), (7 / 7), 8 / 2](这里文字仅前面几行,后面过长)