【深度学习】使用C++手动搭建一个神经网络

1.前言

 深度学习框架给我们带来了很多方便，但是过于依赖框架反而会让我们不知所以然。本篇博客中，我使用C++语言实现了一个简单的神经网络。

2.原理

神经网络由正向传播和反向传播构成。正向传播指的是输入样本数据x，通过一层层网络的计算后得到结果。反向传播值得是通过预测结果与正确结果的差异来对网络中的参数进行修正的过程。

下面我们分别来介绍正向传播算法和反向传播算法：

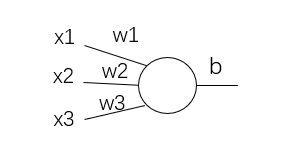
首先以一个最简单的神经元单元为例：

其中x1，x2，x3是一个输入样本的三个数据，输出是y =σ( x1*w1 + x2*w2 + x3*w3 + b)，或者简洁地写成 y = σ(wx + b). 即表示先进行普通的线性操作后，再通过激活函数。为什么要用激活函数呢？因为类似wx + b这样的操作都是线性的，当神经网络层数增加时并不会增加网络的表达性。举例来说：一层的网络的输出是y1 = w1*x1 + b1，二层网络的输出是y2 = w2*y1 + b2，y1 = w1*x1 + b1，也就是y2 = w2*w1*x1 + w2*b1 + b2，就会发现本质上还是一层的网络。激活函数的种类有很多，比如sigmoid、ReLU、tanh等等。

一个基本的神经元就基本介绍完了，许许多多的神经元以不同方式组合，就能构成当今我们所知道的大多数神经网络。

目前的深度学习神经网络一般都由大量的神经元构成，这些神经元相互链接，需要大量的参数来表达。这些参数一般是存在着最优解的，当然也存在着各种各样的局部最优解。为了使神经网络能够自动收敛到最优解，通常需要我们设置好“超参数”，并通过反向传播算法来更新神经网络的参数。

BP算法（error BackPropagation）是反向传播算法的一种，这种算法是最基础的权重调整算法。得益于这些年算力的提升，这种“老”算法得以发挥它的威力。BP算法的核心是链式求导。即 .  除此之外，BP算法还有很多“参数”可供选择，比如损失函数的选择（MSE、CE等）、更新规则的选择（SGD、BGD、MBGD等）等等。在不同的参数选择下，公式细节上会有差异，但是核心推导步骤都是一样的。

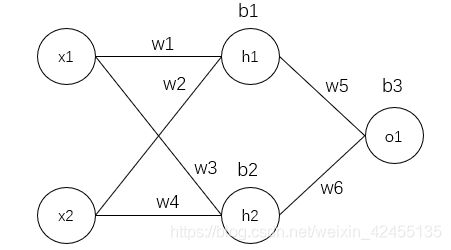
以下图这个神经网络为例：

这个神经网络的激活函数均采用sigmoid，损失函数采用均方误差MSE(Mean-Square Error)，更新方式为随机梯度下降SGD（Stochastic Gradient Descent）。当今网络上大多数的推导也都是这种类型，但并不代表其他的推导就是错的，这点需要注意。

下面列出所有用到的公式：

Sigmoid激活函数：

 

均方误差（MSE）：

其中，n是样本数，这里取1，因为我们是每一个样本更新一次权重。有的时候为了使求导简便，通常还会乘一个1/2.

随机梯度下降（SGD）：

其中，α是学习率，关于学习率的设置也有很多方法，比如：固定学习率衰减、自适应学习率衰减等。

至此，一个最简单的神经网络的基本流程我们已经了解。下面就可以着手代码实现了。

3.代码实现

#include
using namespace std;
double getMSEloss(double x1,double x2){
    return (x1 - x2)*(x1 - x2);
}
class NNetwork
{
    private:
    int epoches;
    double learning_rate;
    double w1,w2,w3,w4,w5,w6;
    double b1,b2,b3;
    public:
    NNetwork(int es,double lr);
    double sigmoid(double x);
    double deriv_sigmoid(double x);
    double forward(vector data);
    void train(vector> data,vector label);
    void predict(vector> test_data,vector test_label);
};
NNetwork::NNetwork(int es,double lr):epoches(es),learning_rate(lr){
    // 超参数、参数初始化
    w1=w2=w3=w4=w5=w6=0;
    b1=b2=b3=0;
}
double NNetwork::sigmoid(double x){
    // 激活函数
    return 1/(1+exp(-x));
}
double NNetwork::deriv_sigmoid(double x){
    // 激活函数求导
    double y = sigmoid(x);
    return y*(1-y);
}
double NNetwork::forward(vector data){
    // 前向传播
    double sum_h1 = w1 * data[0] + w2 * data[1] + b1;
    double h1 = sigmoid(sum_h1);
    double sum_h2 = w3 * data[0] + w4 * data[1] + b2;
    double h2 = sigmoid(sum_h2);
    double sum_o1 = w5 * h1 + w6 * h2 + b3;
    return sigmoid(sum_o1);
}
void NNetwork::train(vector> data,vector label){
    for(int epoch=0;epoch x = data[i];
            double sum_h1 = w1 * x[0] + w2 * x[1] + b1;
            double h1 = sigmoid(sum_h1);
            double sum_h2 = w3 * x[0] + w4 * x[1] + b2;
            double h2 = sigmoid(sum_h2);
            double sum_o1 = w5 * h1 + w6 * h2 + b3;
            double o1 = sigmoid(sum_o1);
            double pred = o1;

            double d_loss_pred = -2 * (label[i] - pred);

            double d_pred_w5 = h1 * deriv_sigmoid(sum_o1);
            double d_pred_w6 = h2 * deriv_sigmoid(sum_o1);
            double d_pred_b3 = deriv_sigmoid(sum_o1);
            
            double d_pred_h1 = w5 * deriv_sigmoid(sum_o1);
            double d_pred_h2 = w6 * deriv_sigmoid(sum_o1);

            double d_h1_w1 = x[0] * deriv_sigmoid(sum_h1);
            double d_h1_w2 = x[1] * deriv_sigmoid(sum_h1);
            double d_h1_b1 = deriv_sigmoid(sum_h1);

            double d_h2_w3 = x[0] * deriv_sigmoid(sum_h2);
            double d_h2_w4 = x[1] * deriv_sigmoid(sum_h2);
            double d_h2_b2 = deriv_sigmoid(sum_h2);

            w1 -= learning_rate * d_loss_pred * d_pred_h1 * d_h1_w1;
            w2 -= learning_rate * d_loss_pred * d_pred_h1 * d_h1_w2;
            b1 -= learning_rate * d_loss_pred * d_pred_h1 * d_h1_b1;
            w3 -= learning_rate * d_loss_pred * d_pred_h2 * d_h2_w3;
            w4 -= learning_rate * d_loss_pred * d_pred_h2 * d_h2_w4;
            b2 -= learning_rate * d_loss_pred * d_pred_h2 * d_h2_b2;
            w5 -= learning_rate * d_loss_pred * d_pred_w5;
            w6 -= learning_rate * d_loss_pred * d_pred_w6;
            b3 -= learning_rate * d_loss_pred * d_pred_b3; 
        }
        if(epoch%10==0){
            double loss = 0;
            for(int i=0;i> test_data,vector test_label){
    int n = test_data.size();
    double cnt = 0;
    for(int i=0;i0.5?1:0;
        cnt += (test_label[i]==pred);
    }
    cout<<"correct rate:"<> data = {{-2,-1},{25,6},{17,4},{-15,-6}};
    vector label = {1,0,0,1};
    NNetwork network = NNetwork(1000,0.1);
    network.train(data,label);
    vector> test_data  = {{-3,-4},{-5,-4},{12,3},{-13,-4},{9,12}};
    vector test_label = {1,1,0,1,0};
    network.predict(test_data,test_label);
    return 0;
}

4.实验结果

经过了990次的训练，损失函数从0.99降到0.0012，准确率为100%。

5.总结

本篇博客中实现的仅仅是一个简单的神经网络，在这篇博客中，我们使用C++简单实现了正向传播、反向传播。得益于C++的良好封装性，我们甚至可以基于此开发一个基于C++的神经网络库（mxnet等），其运算效率势必会优于python。