（转载）直观理解ROC曲线中AUC评价指标

导语

最近一直在思考如何直观理解AUC，查了维基百科的以及网上的讲解描述，感觉仍然很难把这个概念表述得通俗易懂，直到昨天周会后拿笔在纸上画了画，感觉似乎找到了一种比较有意思的理解方法，下面就请各位看官容我慢慢道来。首先简单介绍一下什么是AUC。

根据维基百科的描述，AUC（Area under the Curve of ROC）是ROC曲线下方的面积，是判断二分类预测模型优劣的标准。ROC（receiver operating characteristic curve）接收者操作特征曲线，是由二战中的电子工程师和雷达工程师发明用来侦测战场上敌军载具（飞机、船舰）的指标，属于信号检测理论。ROC曲线的横坐标是伪阳性率（也叫假正类率，False Positive Rate），纵坐标是真阳性率（真正类率，True Positive Rate），相应的还有真阴性率（真负类率，True Negative Rate）和伪阴性率（假负类率，False Negative Rate）。这四类的计算方法如下：

• 伪阳性率（FPR）
  在所有实际为阴性的样本中，被错误地判断为阳性的比率。
• 真阳性率（TPR）
  在所有实际为阳性的样本中，被正确地判断为阳性的比率。
• 伪阴性率（FNR）
  在所有实际为阳性的样本中，被错误的预测为阴性的比率。
• 真阴性率（TNR）
  在所有实际为阴性的样本中，被正确的预测为阴性的比率。

x轴与y轴的值域都是[0, 1]，随着判定正例的阈值不断增加，我们可以得到一组(x, y)的点，相连便作出了ROC曲线，示例图如下：

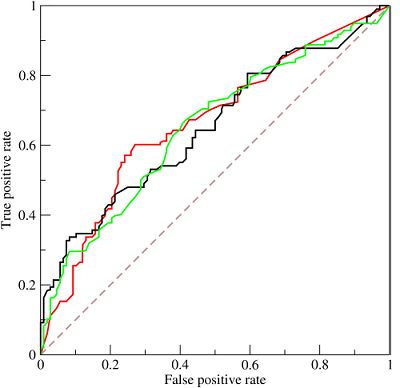
图中的虚线相当于随机预测的结果。不难看出，随着FPR的上升，ROC曲线从原点(0, 0)出发，最终都会落到(1, 1)点。AUC便是其右下方的曲线面积。下图展现了三种AUC的值：

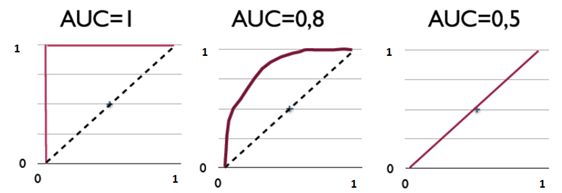
AUC对于每一个做机器学习的人来说一定不陌生，它是衡量二分类模型优劣的一种评价指标，表示正例排在负例前面的概率。其他评价指标有精确度、准确率、召回率，而AUC比这三者更为常用。因为一般在分类模型中，预测结果都是以概率的形式表现，如果要计算准确率，通常都会手动设置一个阈值来将对应的概率转化成类别，这个阈值也就很大程度上影响了模型准确率的计算。我们不妨举一个极端的例子：一个二类分类问题一共10个样本，其中9个样本为正例，1个样本为负例，在全部判正的情况下准确率将高达90%，而这并不是我们希望的结果，尤其是在这个负例样本得分还是最高的情况下，模型的性能本应极差，从准确率上看却适得其反。而AUC能很好描述模型整体性能的高低。这种情况下，模型的AUC值将等于0（当然，通过取反可以解决小于50%的情况，不过这是另一回事了）。

那么，如何理解这个ROC的曲线面积AUC的数学意义呢？

---

优雅理解法

我想，既然是计算面积，能否像时间速度曲线一样，套用积分计算路程的思路去理解呢？这个问题思考了许久，始终没能把真阳性率与速度、伪阳性率与时间挂上钩。众所周知，时间速度曲线图如下：

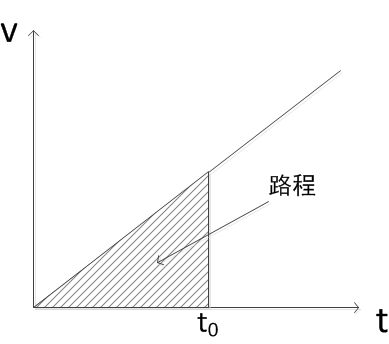
图中阴影部分的面积便是路程，因为上图x轴上的任意两值相减得到的时间差是有直观意义的。相比之下，ROC中假阳性率相减则并没有如此直观的概念。ROC图从直观上看能得出两个结论：曲线点越接近右下角表示当前阈值预测正例出错的概率越高，准确性较低；曲线点越接近左上角则代表预测正例出错的概率越低，准确性较高。如下图：

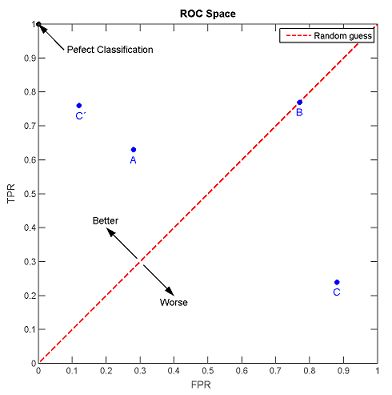
对比之后发现，时间速度曲线是连续的，而ROC曲线是由一组离散的点组成，因为在一般情况下，分类的样本空间有限。其点总数其实就是样本总数，y轴最小步长为1/样本正例数，x轴的最小步长则是1/样本负例数。既然曲线点可枚举，那么我们就可以多举举栗子。

现在假设有一个训练好的二分类器对10个正负样本（正例5个，负例5个）预测，得分按高到低排序得到的最好预测结果为[1, 1, 1, 1, 1, 0, 0, 0, 0, 0]，即5个正例均排在5个负例前面，正例排在负例前面的概率为100%。然后绘制其ROC曲线，由于是10个样本，除开原点我们需要描10个点，如下：

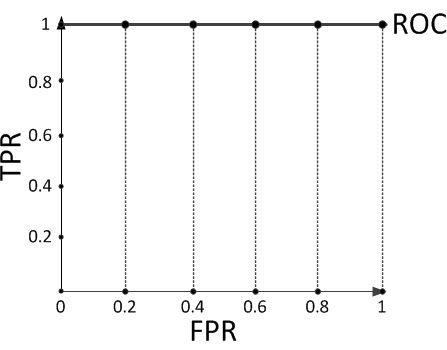
描点方式按照样本预测结果的得分高低从左至右开始遍历。从原点开始，每遇到1便向y轴正方向移动y轴最小步长1个单位，这里是1/5=0.2；每遇到0则向x轴正方向移动x轴最小步长1个单位，这里也是0.2。不难看出，上图的AUC等于1，印证了正例排在负例前面的概率的确为100%。

我们不妨再举个栗子，预测结果序列为[1, 1, 1, 1, 0, 1, 0, 0, 0, 0]。

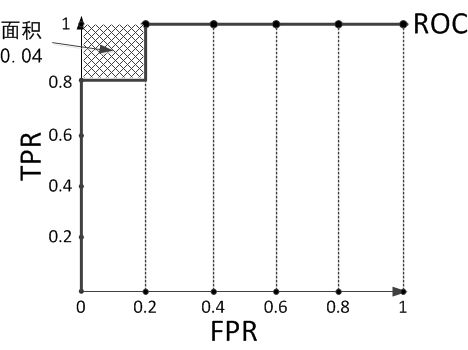
计算上图的AUC为0.96与计算正例与排在负例前面的概率0.8 × 1 + 0.2 × 0.8 = 0.96相等，而左上角阴影部分的面积则是负例排在正例前面的概率0.2 × 0.2 = 0.04。

再看个栗子，预测结果序列为[1, 1, 1, 0, 1, 0, 1, 0, 0, 0]。

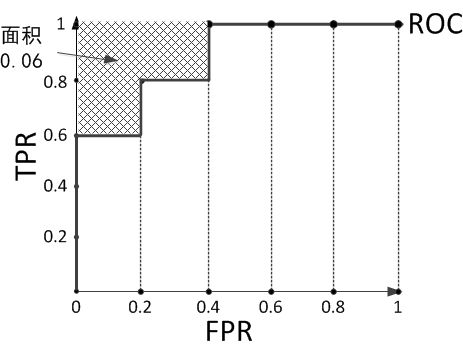
计算上图的AUC为0.88与计算正例与排在负例前面的概率0.6 × 1 + 0.2 × 0.8 + 0.2 × 0.6 = 0.88相等，左上角阴影部分的面积是负例排在正例前面的概率0.2 × 0.2 × 3 = 0.12。

---

结语

至此，我们便可直观理解ROC曲线图上面积的含义了，这相当于给定最小时间单位下分段递增匀速运动时间速度曲线的路程积分问题。TPR相当于速度，每段“时间”的起始TPR越高，这段“时间”内正例排在负例前面的概率也就越大，而这个概率就是路程；FPR则相当于时间，这个可以这么理解：每次旅行总会结束，而FPR也总会到达100%（x值为1），FPR每向x轴正方向移动一步，相当于离“旅行结束”又近了一步。这样，一个积分概率，一个积分路程，大概就能近似理解了。

在此感谢各位看官的耐心阅读。后续内容将会不定期奉上，欢迎大家关注小斗公众号 对半独白！

---