卷积神经网络

Datawhale开源学习，机器学习课程，项目地址：https://github.com/datawhalechina/leeml-notes

Convolutional Neural Network

本节内容学习了什么是CNN卷积神经网络，相比于全连接网络，它每次只提取部分内容作为整个网络的某些模块的运算，每个卷积可能负责图像上某个小模块的内容，比如某个卷积filter输出后得到的可能是某个该卷积想关注的图像纹理特征，我们一般是将多个卷积最终通过全连接，让局部信息和全局信息相互作用，通过全连接最终利用起整体的信息，所以也会说明卷积神经网络和全连接神经网络之间的关系，以及卷积神经网络的一些应用，比如卷积神经网络可以用于文本情感分析、语音辨识、迁移学习等等涉及图像的操作上。

接下来我会放出经过自己整理的李宏毅老师的讲课笔记。

Notes

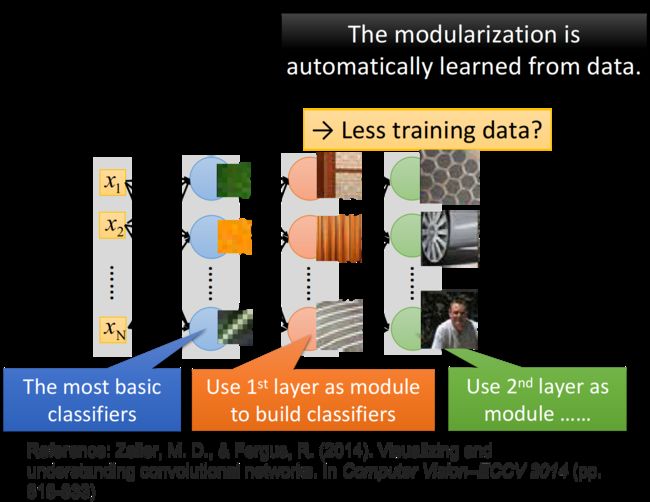
我们可以用一般的neural network来做影像处理，不一定要用CNN，比如说你想要做图像的分类，那你就去train一个neural network，它的input是一张图片，你就用里面的pixel来表示这张图片，也就是一个很长很长的vector，而output则是由图像类别组成的vector，假设你有1000个类别，那output就有1000个dimension。但是，我们现在会遇到的问题是这样子：实际上，在train neural network时，我们会有一种期待说，在这个network structure里面的每一个neuron，都应该代表了一个最基本的classifier；事实上，在文献上，根据训练的结果，也有很多人得到这样的结论，举例来说，下图中：

• 第一个layer的neuron，它就是最简单的classifier，它做的事情就是detect有没有绿色出现、有没有黄色出现、有没有斜的条纹出现等等
• 那第二个layer，它做的事情是detect更复杂的东西，根据第一个layer的output，它如果看到直线横线，就是窗框的一部分；如果看到棕色的直条纹就是木纹；看到斜条纹加灰色的，这个有可能是很多东西，比如说，轮胎的一部分等等
• 再根据第二个hidden layer的output，第三个hidden layer会做更复杂的事情，比如它可以知道说，当某一个neuron看到蜂巢，它就会被activate；当某一个neuron看到车子，它就会被activate；当某一个neuron看到人的上半身，它就会被activate等等

那现在的问题是：当我们直接用一般的fully connected的feedforward network来做图像处理的时候，往往会需要太多的参数。因此引入卷积神经网络CNN。

举例来说，假设这是一张$100\times 100$的彩色图片，它的分辨率才$100\times 100$，那这已经是很小张的image了，然后你需要把它拉成一个vector，总共有$100\times 100\times 3$个pixel（如果是彩色的图的话，每个pixel其实需要3个value，即RGB值来描述它的），把这些加起来input vector就已经有三万维了；如果input vector是三万维，又假设hidden layer有1000个neuron，那仅仅是第一层hidden layer的参数就已经有$30000\times 1000$个了，这样就太多了。所以，CNN做的事情其实是，来简化这个neural network的架构，我们根据自己的知识和对图像处理的理解，一开始就把某些实际上用不到的参数给过滤掉。我们一开始就想一些办法，不要用fully connected network，而是用比较少的参数，来做图像处理这件事情，所以CNN其实是比一般的DNN还要更简单的。

以上内容说的意思就是，卷积网络只需要提取图像中「一部分」有用的信息，而不需要像全连接那样利用所有的信息，一方面是突出有用信息，过滤掉不切实际或对最终结果几乎没有帮助的信息；另一方面也考虑到硬件层面，CNN运算量相对较低。

---

接下来我去进一步说明，为什么通过卷积只提取图像的「一部分」信息就可以呢？拿掉这一部分数据为何还可以处理图像？李宏毅做了三点说明：

1. Some patterns are much smaller than the whole image（有些图像只需要关注图像的一部分区域内容即可）
2. The same patterns appear in different regions（同样的内容可能出现在不同图片的不同位置，CNN可以屏蔽位置对图像信息的影响）
3. Subsampling the pixels will not change the object（采用一些下采样方法后对图像的整体信息不会有太多损失）

接下来就是对上面问题「为什么拿掉一部分数据还可以处理图像」的进行解答和说明。

Why CNN for Image？

为什么我们有可能把一些参数拿掉？为什么我们有可能只用比较少的参数就可以来做图像处理这件事情？下面列出三个对影像处理的观察，这也是CNN架构提出的基础所在。

1. Some patterns are much smaller than the whole image

在影像处理里面，如果在network的第一层hidden layer里，那些neuron要做的事情是侦测有没有一种东西、一种pattern（图案样式）出现，那大部分的pattern其实是比整张image要小的，所以对一个neuron来说，想要侦测有没有某一个pattern出现，它其实并不需要看整张image，只需要看这张image的一小部分，就可以决定这件事情了。

举例来说，假设现在我们有一张鸟的图片，那第一层hidden layer的某一个neuron的工作是，检测有没有鸟嘴的存在（你可能还有一些neuron侦测有没有鸟嘴的存在、有一些neuron侦测有没有爪子的存在、有一些neuron侦测有没有翅膀的存在、有没有尾巴的存在，之后合起来，就可以侦测，图片中有没有一只鸟），那它其实并不需要看整张图，因为，其实我们只要给neuron看个小的区域，它其实就可以知道说，这是不是一个鸟嘴，对人来说也是一样，只要看这个小的区域你就会知道说这是鸟嘴，所以，每一个neuron其实只要连接到一个小块的区域就好，它不需要连接到整张完整的图，因此也对应着更少的参数

2. The same patterns appear in different regions

同样的pattern，可能会出现在image的不同部分，但是它们有同样的形状、代表的是同样的含义，因此它们也可以用同样的neuron、同样的参数，被同一个detector检测出来

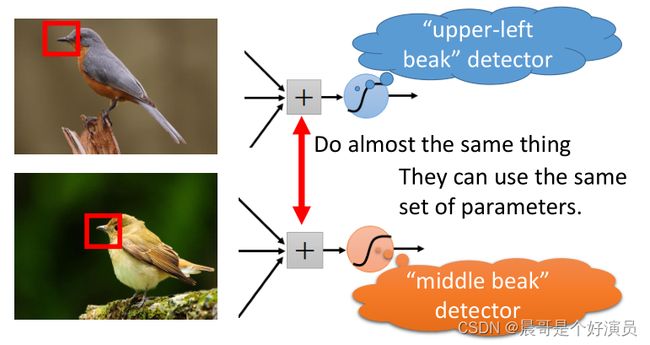
举例来说，图中分别有一个处于左上角的鸟嘴和一个处于中央的鸟嘴，但你并不需要训练两个不同的detector去专门侦测左上角有没有鸟嘴和中央有没有鸟嘴这两件事情，这样做太冗余了，我们要cost down(降低成本)，我们并不需要有两个neuron、两组不同的参数来做duplicate的事情，所以我们可以要求这些功能几乎一致的neuron共用一组参数，它们share同一组参数就可以帮助减少总参数的量

3. Subsampling the pixels will not change the object

我们可以对一张image做subsampling，假如你把它奇数行、偶数列的pixel拿掉，image就可以变成原来的十分之一大小，而且并不会影响人对这张image的理解，对你来说，下面两张大小不一的image看起来不会有什么太大的区别，你都可以识别里面有什么物件，因此subsampling对图像辨识来说，可能是没有太大的影响的

所以，我们可以利用subsampling这个概念把image变小，从而减少需要用到的参数量

The whole CNN structure

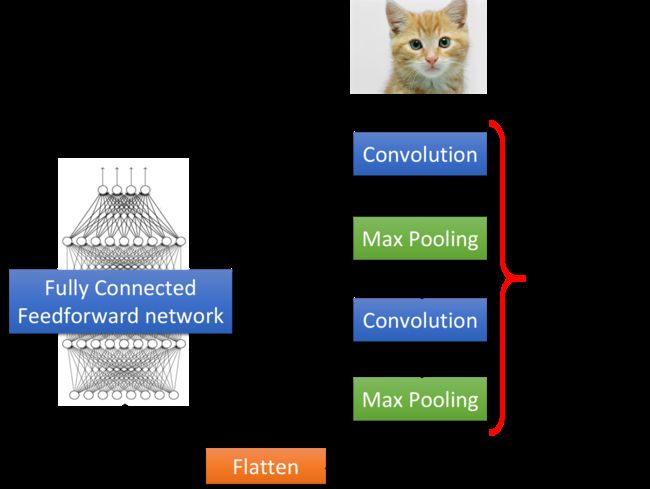
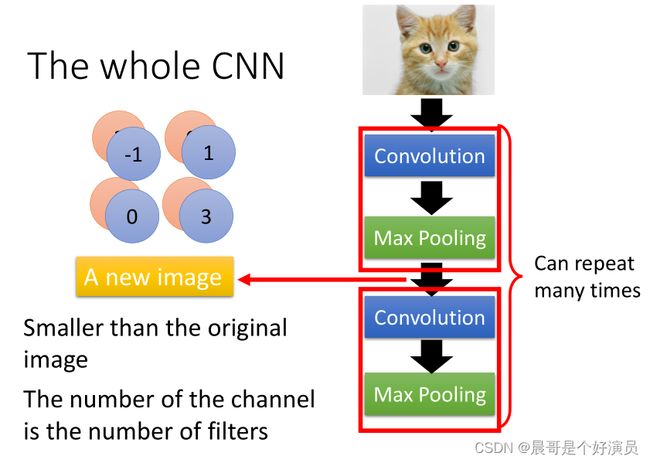
整个CNN的架构是这样的：首先，input一张image以后，它会先通过Convolution的layer，接下来做Max Pooling这件事，然后再去做Convolution，再做Max Pooling。这个process可以反复进行多次（重复次数需要事先决定），这就是network的架构，就好像network有几层一样，你要做几次convolution，做几次Max Pooling，在定这个network的架构时就要事先决定好。当你做完先前决定的convolution和max pooling的次数后，你要做的事情是Flatten，做完flatten以后，你就把Flatten output丢到一般的Fully connected network里面去，最终得到影像辨识的结果：

我们基于之前提到的三个对影像处理的观察，设计了CNN这样的架构，第一个是要侦测一个pattern，你不需要看整张image，只要看image的一个小部分；第二个是同样的pattern会出现在一张图片的不同区域；第三个是我们可以对整张image做subsampling。前面两个property，是用convolution的layer来处理的；最后这个property，是用max pooling来处理的。

以上实际上是说卷积适用于图像处理，同时说了卷积和最大池化max pooling是以何种形式存放于整个网络中的，又是怎样和全连接联系到一起的。

Convolution卷积

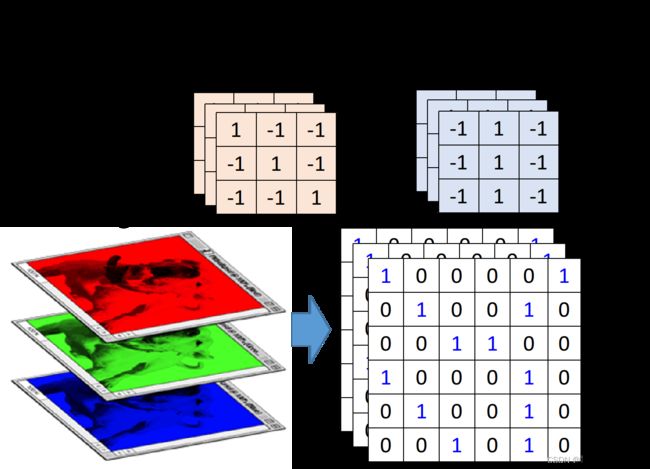
假设现在我们network的input是一张6$\times 6$的image，图像是黑白的，因此每个pixel只需要用一个value来表示，而在convolution layer里面，有一堆Filter，这边的每一个Filter，其实就等同于是Fully connected layer里的一个neuron。

Property 1

每一个Filter其实就是一个matrix，这个matrix里面每一个element的值，就跟那些neuron的weight和bias一样，是network的parameter，它们具体的值都是通过Training data学出来的，而不是人去设计的。所以，每个Filter里面的值是什么，要做什么事情，都是自动学习出来的，图中每一个filter是$3\times 3$的size，意味着它就是在侦测一个$3\times 3$的pattern，当它侦测的时候，并不会去看整张image，它只看一个$3\times 3$范围内的pixel，就可以判断某一个pattern有没有出现，这就考虑了property 1

Property 2

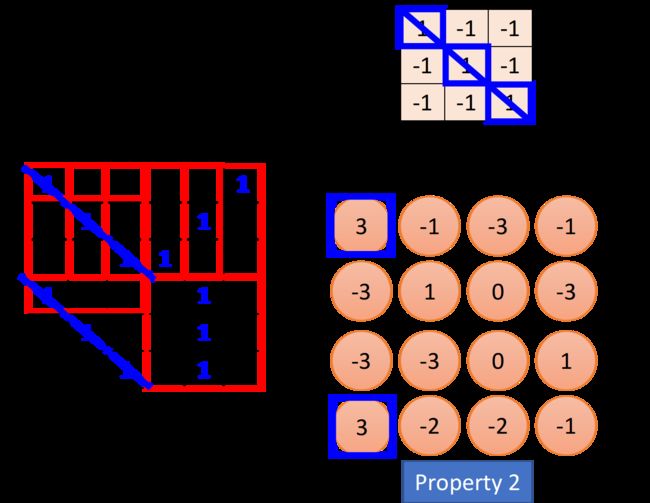
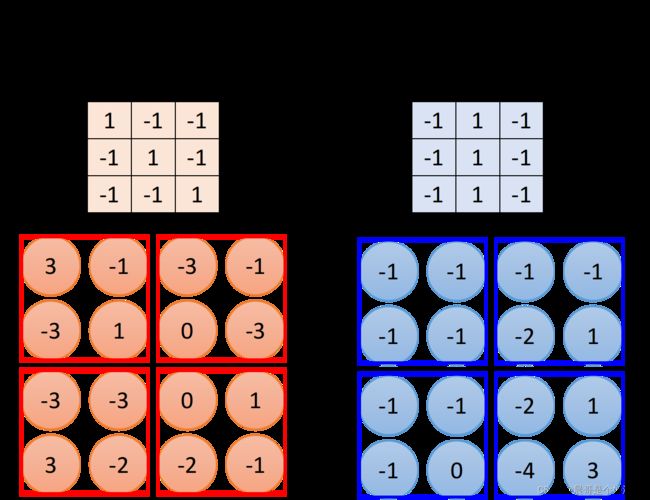
这个filter是从image的左上角开始，做一个slide window，每次向右挪动一定的距离，这个距离就叫做stride（步长），由自己设定，每次filter停下时就跟image中对应的$3\times 3$的matrix做一个内积（相同位置的值相乘并累计求和），这里假设stride=1，那么我们的filter每次移动一格，当它碰到image最右边的时候，就从下一行的最左边开始重复进行上述操作，经过一整个convolution的process，最终得到下图所示的红色的$4\times 4$ matrix。

观察上图中的Filter 1，它斜对角的地方是1,1,1，所以它的工作就是detect有没有连续的从左上角到右下角的1,1,1出现在这个image里面，检测到的结果已在上图中用蓝线标识出来，此时filter得到的卷积结果的左上和左下得到了最大的值，这就代表说，该filter所要侦测的pattern出现在image的左上角和左下角。同一个pattern出现在image左上角的位置和左下角的位置，并不需要用到不同的filter，我们用filter 1就可以侦测出来，这就考虑了property 2。

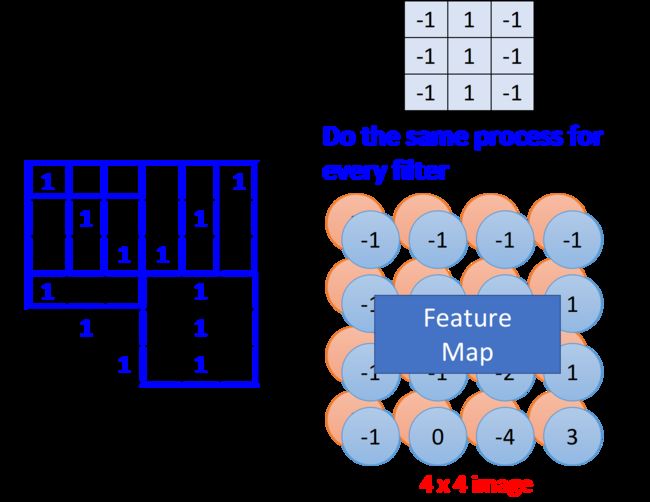
Feature Map

在一个convolution的layer里面，它会有一打filter，不一样的filter会有不一样的参数，但是这些filter做卷积的过程都是一模一样的，你把filter 2跟image做完convolution以后，你就会得到另外一个蓝色的$4\times 4$ matrix，那这个蓝色的$4\times 4$ matrix跟之前红色的$4\times 4$matrix合起来，他们就叫做Feature Map，有多少个filter，对应就有多少个映射后的image，filter的数量等于feature map的数量。

CNN对不同scale的相同pattern的处理上存在一定的困难，由于现在每一个filter size都是一样的，这意味着，如果你今天有同一个pattern，它有不同的size，有大的鸟嘴，也有小的鸟嘴，CNN并不能够自动处理这个问题；

DeepMind曾经发过一篇paper，提到了当你input一张image时，它在CNN前面再接另外一个network，这个network做的事情是，它会output一些scalar，告诉你它要把这个image的里面的哪些位置做旋转、缩放，然后，再丢到CNN里面，这样你其实会得到比较好的performance。

Colorful image

刚才举的例子是黑白的image，所以你input的是一个matrix，如果今天是彩色的image会怎么样呢？我们知道彩色的image就是由RGB组成的，所以一个彩色的image，它就是好几个matrix叠在一起，是一个立方体，如果我今天要处理彩色的image，要怎么做呢？

这个时候你的filter就不再是一个matrix了，它也会是一个立方体，如果你今天是RGB这三个颜色来表示一个pixel的话，那你的input就是$3\times 6\times \times 6$，你的filter就是$3\times 3\times 3$，你的filter的高就是3，在做convolution的话，就是将filter的9个值和image的9个值做内积，不是把每一个channel分开来算，而是合在一起来算，一个filter就考虑了不同颜色所代表的channel，具体操作为做内积，并且三层的结果相加，得到一个scalar，因此一个filter可以得到一个feature map，并且层数只能为1层。图中的这种情况，输出的feature map有2个channel，分别是filter 1和filter 2与原图卷积得到的矩阵。

以上内容说明了如何在单通道黑白图像和三通道RGB图像上进行卷积运算，强调了什么是filter，什么是Channel等等易混淆概念。

Convolution v.s. Fully connected

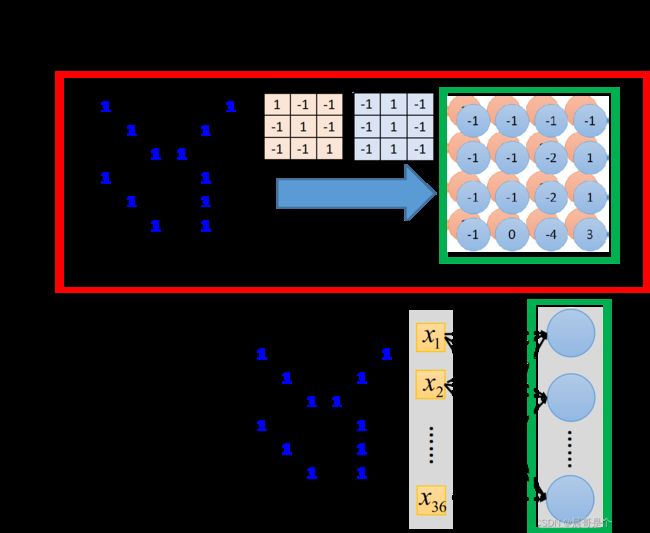
接下来要讲的是，convolution跟fully connected有什么关系，你可能觉得它是一个很特别的operation，感觉跟neural network没半毛钱关系，其实它就是一个neural network。卷积其实就是fully connected的layer把一些weight拿掉而已，下图中绿色方框标识出的feature map的output，其实就是hidden layer的neuron的output。

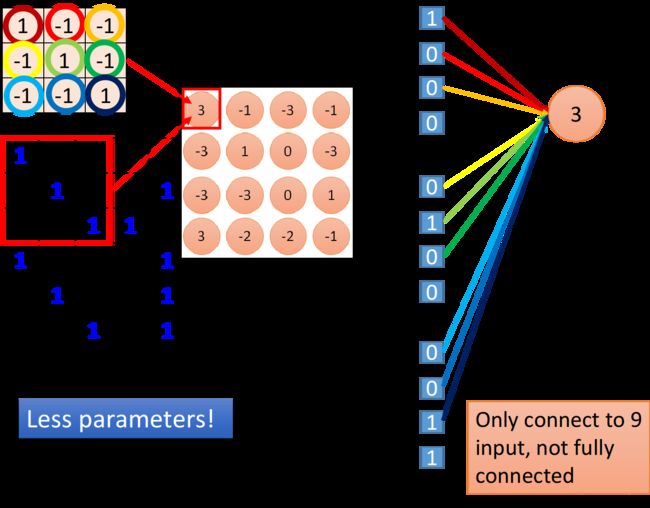
接下来我们来解释这件事情，如下图所示，我们在做convolution时，把filter放在image的左上角，然后再去做inner product，得到一个值3；这件事情等同于，我们现在把这个image的$6\times 6$的matrix拉直变成右边这个用于input的vector，然后，你有一个neuron，这些input经过这个neuron之后，得到的output是3，那这个neuron的output怎么来的呢？这个neuron实际上就是由filter转化而来的，我们把filter放在image的左上角，此时filter考虑的就是和它重合的9个pixel，假设你把这一个$6\times 6$的image的36个pixel拉成直的vector作为input，那这9个pixel分别就对应着右侧编号1，2，3的pixel，编号7，8，9的pixel跟编号13，14，15的pixel。

如果我们说这个filter和image matrix做inner product以后得到的output 3，就是input vector经过某个neuron得到的output 3的话，这就说明存在这样一个neuron，这个neuron带weight的连线，就只连接到编号为1，2，3，7，8，9，13，14，15的这9个pixel而已，而这个neuron和这9个pixel连线上所标注的的weight就是filter matrix里面的这9个数值，作为对比，Fully connected的neuron是必须连接到所有36个input上的，但是我们现在只用连接9个input，因为我们知道要detect一个pattern，不需要看整张image，看9个input pixel就够了，所以当我们这么做的时候，就用了比较少的参数（这也就是本文一开始说到的，卷积相比于全连接而言，用到更少的参数）

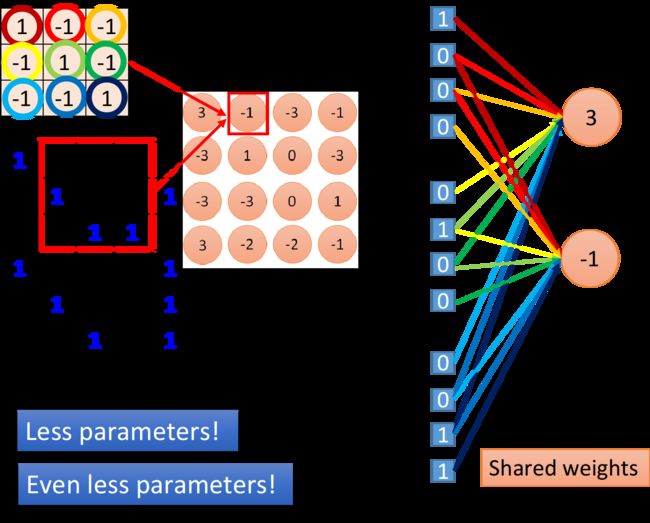
当我们把filter做stride = 1的移动的时候，会发生什么事呢？此时我们通过filter和image matrix的内积得到另外一个output值-1，我们假设这个-1是另外一个neuron的output，那这个neuron会连接到哪些input呢？下图中这个框起来的地方正好就对应到pixel 2，3，4，pixel 8，9，10跟pixel 14，15，16，你会发现output为3和-1的这两个neuron，它们分别去检测在image的两个不同位置上是否存在某个pattern，因此在Fully connected layer里它们做的是两件不同的事情，每一个neuron应该有自己独立的weight。

但是，当我们做这个convolution的时候，首先我们把每一个neuron前面连接的weight减少了，然后我们强迫某些neuron（比如图中output为3和-1的两个neuron），它们一定要共享一组weight，虽然这两个neuron连接到的pixel对象各不相同，但它们用的weight都必须是一样的，等于filter里面的元素值。这件事情就叫做weight share，当我们做这件事情的时候，用的参数，又会比原来更少。

因此我们可以这样想，有这样一些特殊的neuron，它们只连接着9条带weight的线（$9=3\times 3$对应着filter的元素个数，这些weight也就是filter内部的元素值，上图中圆圈的颜色与连线的颜色一一对应）。当filter在image matrix上移动做convolution的时候，每次移动做的事情实际上是去检测这个地方有没有某一种pattern，对于Fully connected layer来说，它是对整张image做detection的，因此每次去检测image上不同地方有没有pattern其实是不同的事情，所以这些neuron都必须连接到整张image的所有pixel上，并且不同neuron的连线上的weight都是相互独立的。对于convolution layer来说，首先它是对image的一部分做detection的，因此它的neuron只需要连接到image的部分pixel上，对应连线所需要的weight参数就会减少；

其次由于是用同一个filter去检测不同位置的pattern，所以这对convolution layer来说，其实是同一件事情，因此不同的neuron，虽然连接到的pixel对象各不相同，但是在“做同一件事情”的前提下，也就是用同一个filter的前提下，这些neuron所使用的weight参数都是相同的，通过这样一种weight share的方式，再次减少network所需要用到的weight参数。

CNN的本质，就是减少参数的过程。

以上内容说明了CNN相比全连接来说，减少了很多参数。首先当前卷积只取前一层输入的局部节点进行下一轮输出训练；其次多个节点之间可共享参数。

Training

看到这里你可能会问，这样的network该怎么搭建，又该怎么去train呢？首先，第一件事情就是这都是用toolkit做的，所以你大概不会自己去写；如果你要自己写的话，它其实就是跟原来的Backpropagation用一模一样的做法，只是有一些weight就永远是0，你就不去train它，它就永远是0。然后，怎么让某些neuron的weight值永远都是一样呢？你就用一般的Backpropagation的方法，对每个weight都去算出gradient，再把本来要tight在一起、要share weight的那些weight的gradient平均，然后，让他们update同样值就ok了。

---

Max Pooling

Operation of max pooling

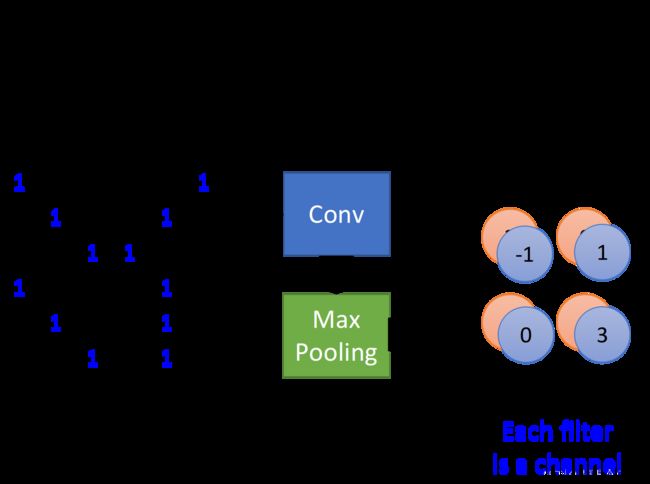
相较于convolution，max pooling是比较简单的，它就是做subsampling，根据filter 1，我们得到一个$4\times 4$的matrix，根据filter 2，你得到另外一个$4\times 4$的matrix，接下来，我们要做什么事呢？我们把output四个分为一组，每一组里面通过选取平均值或最大值的方式，把原来4个value合成一个 value，这件事情相当于在image每相邻的四块区域内都挑出一块来检测，这种subsampling的方式就可以让你的image缩小。

讲到这里你可能会有一个问题，如果取Maximum放到network里面，不就没法微分了吗？max这个东西，感觉是没有办法对它微分的啊，其实是可以的，类比Maxout network，你就知道怎么用微分的方式来处理它。

The whole CNN

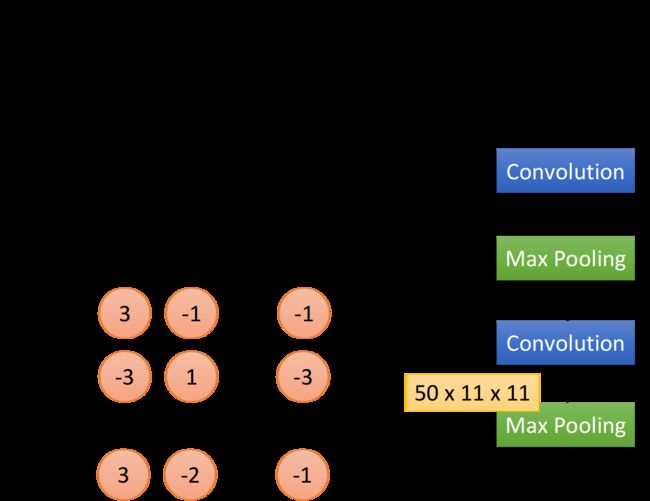
做完一次convolution加一次max pooling，我们就把原来$6\times 6$的image，变成了一个$2\times 2$的image；至于这个$2\times 2$的image，它每一个pixel的深度，也就是每一个pixel用几个value来表示，就取决于你有几个filter，如果你有50个filter，就是50维，像下图中是两个filter，对应的深度就是两维，得到结果就是一个new smaller image，一个filter就代表了一个channel。

所以，这是一个新的比较小的image，它表示的是不同区域上提取到的特征，实际上不同的filter检测的是该image同一区域上的不同特征属性，所以每一层channel代表的是一种属性，一块区域有几种不同的属性，就有几层不同的channel，对应的就会有几个不同的filter对其进行convolution操作，Each filter is a channel。

这件事情可以repeat很多次，你可以把得到的这个比较小的image，再次进行convolution和max pooling的操作，得到一个更小的image，依次类推。

有这样一个问题（我之前也一直有这样的疑问，最后终于理解每次卷积实际上是整个Channel上的卷积运算，下一次Channel的个数和当前filter数量有关系）：假设我第一个convolution有25个filter，通过这些filter得到25个feature map，然后repeat的时候第二个convolution也有25个filter，那这样做完，我是不是会得到$25^2$个feature map？

其实不是这样的，你这边做完一次convolution，得到25个feature map之后再做一次convolution，还是会得到25个feature map，因为convolution在考虑input的时候，是会考虑深度的（这里的意思就是卷积操作是会考虑Channel的，每次卷积是按照所有Channel去做卷积），它并不是每一个channel分开考虑，而是一次考虑所有的channel，所以，你convolution这边有多少个filter，再次output的时候就会有多少个channel，The number of the channel is the number of filters，只不过下一次convolution时，25个filter都是一个立方体，它的高有25个value那么高。

这件事可以repeat很多次，通过一个convolution + max pooling就得到新的 image。它是一个比较小的image，可以把这个小的image，做同样的事情，再次通过convolution + max pooling，将得到一个更小的image。

filter

• 假设我们input是一个$1\times 28\times 28$的image。
• 通过25个filter的convolution layer以后你得到的output，会有25个channel，又因为filter的size是$3\times 3$，因此如果不考虑image边缘处的处理的话，得到的channel会是26$\times 26$的，因此通过第一个convolution得到$25\times 26\times 26$的cubic image。
• 接下来就是做Max pooling，把$2\times 2$的pixel分为一组，然后从里面选一个最大的组成新的image，大小为$25\times 13\times 13$。
• 再做一次convolution，假设这次选择50个filter，每个filter size是$3\times 3$的话，output的channel就变成有50个，那13*13的image，通过$3\times 3$的filter，就会变成$11\times 11$，因此通过第二个convolution得到$50\times 11\times 11$的image。
• 再做一次Max Pooling，变成$50\times 5\times 5$。

在第一个convolution里面，每一个filter都有9个参数，它就是一个$3\times 3$的matrix；但是在第二个convolution layer里面，虽然每一个filter都是$3\times 3$，但它其实不是$3\times 3$个参数，因为它的input是一个$25\times 13\times 13$的cubic，这个cubic的channel有25个，所以要用同样高度的cubic filter对它进行卷积，于是我们的filter实际上是一个$25\times 3\times 3$的cubic，所以第二个convolution layer这边每个filter共有225个参数

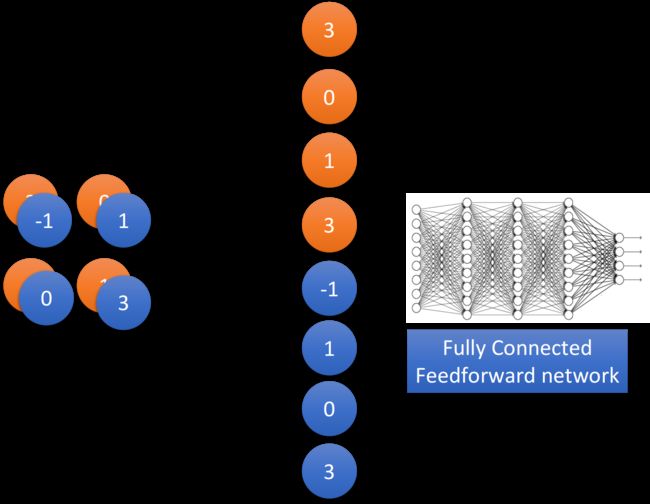
通过两次convolution和max pooling的组合，最终的image变成了$50\times 5\times 5$的size，然后使用Flatten将这个image拉直，变成一个1250维的vector，再把它丢到一个Fully Connected Feedforward network里面，network structure就搭建完成了。看到这里，你可能会有一个疑惑，第二次convolution的input是$25\times 13\times 13$的cubic，用50个$3\times 3$的filter卷积后，得到的输出时应该是50个cubic，且每个cubic的尺寸为$25\times 11\times 11$，那么max pooling把长宽各砍掉一半后就是50层$25\times 5\times 5$的cubic，那flatten后不应该就是$50\times 25\times 5\times 5$吗？

其实不是这样的，在第二次做convolution的时候，我们是用$25\times 3\times 3$的cubic filter对$25\times 13\times 13$的cubic input进行卷积操作的，filter的每一层和input cubic中对应的每一层（也就是每一个channel），它们进行内积后，还要把cubic的25个channel的内积值进行求和，作为这个「neuron」的output，它是一个scalar，这个cubic filter对整个cubic input做完一遍卷积操作后，得到的是一层scalar，然后有50个cubic filter，对应着50层scalar，因此最终得到的output是一个$50\times 11\times 11$的cubic。

这里的关键是filter和image都是cubic，每个cubic filter有25层高，它和同样有25层高的cubic image做卷积，并不是单单把每个cubic对应的channel进行内积，还会把这些内积求和，最终变为1层。因此两个矩阵或者tensor做了卷积后，不管之前的维数如何，都会变为一个scalar。故如果有50个Filter，无论input是什么样子的，最终的output还会是50层。

以上就是对卷积运算的说明，特别是上面提的一个问题，能够让人更了解若图像Channel不为1，那此时的卷积运算该如何运算（由内积+求和两部分组成）。

Flatten

做完convolution和max pooling之后，就是Flatten和Fully connected Feedforward network的部分。Flatten的意思是，把左边的feature map拉直，然后把它丢进一个Fully connected Feedforward network，然后就结束了，也就是说，我们之前通过CNN提取出了image的feature，它相较于原先一整个image的vector，少了很大一部分内容，因此需要的参数也大幅度地减少了，但最终，也还是要丢到一个Fully connected的network中去做最后的分类工作。

What does CNN learn？

如果今天有一个方法，它可以让你轻易地理解为什么这个方法会下这样的判断和决策的话，那其实你会觉得它不够intelligent；它必须要是你无法理解的东西，这样它才够intelligent，至少你会感觉它很intelligent。所以，大家常说deep learning就是一个黑盒子，你learn出来以后，根本就不知道为什么是这样子，于是你会感觉它很intelligent，但是其实还是有很多方法可以分析的，今天我们就来示范一下怎么分析CNN，看一下它到底学到了什么。

要分析第一个convolution的filter是比较容易的，因为第一个convolution layer里面，每一个filter就是一个$3\times 3$的matrix，它对应到$3\times 3$范围内的9个pixel，所以你只要看这个filter的值，就可以知道它在detect什么东西，因此第一层的filter是很容易理解的。

但是你比较没有办法想像它在做什么事情的，是第二层的filter，它们是50个同样为$3\times 3$的filter，但是这些filter的input并不是pixel，而是做完convolution再做Max pooling的结果，因此filter考虑的范围并不是$3\times 3=9$个pixel，而是一个长宽为$3\times 3$，高为25的cubic，filter实际在image上看到的范围是远大于9个pixel的，所以你就算把它的weight拿出来，也不知道它在做什么。

那我们怎么来分析一个filter它做的事情是什么呢？你可以这样做：我们知道在第二个convolution layer里面的50个filter，每一个filter的output就是一个$11\times 11$的matrix，假设我们现在把第k个filter的output拿出来，如下图所示，这个matrix里的每一个element，我们叫它$a_{ij}^k$，上标k表示这是第k个filter，下标$ij$表示它在这个matrix里的第i个row，第j个column。

接下来我们define一个$a^k$叫做Degree of the activation of the k-th filter，这个值表示现在的第k个filter，它有多被activate，直观来讲就是描述现在input的东西跟第k个filter有多接近，它对filter的激活程度有多少。第k个filter被启动的degree $a^k$就定义成，它与input进行卷积所输出的output里所有element的summation，以上图为例，就是这$11\times 11$的output matrix里所有元素之和，用公式描述如下：
$$a^k=\sum _{i=1}^{11}\sum _{j=1}^{11}{a}_{ij}^k$$
也就是说，我们input一张image，然后把这个filter和image进行卷积所output的$11\times 11$个值全部加起来，当作现在这个filter被activate的程度。接下来我们要做的事情是这样子，我们想要知道第k个filter的作用是什么，那我们就要找一张image，这张image可以让第k个filter被activate的程度最大；于是我们现在要解的问题是，找一个image x，它可以让我们定义的activation的degree $a^k$最大，即：
$$x^{\ast }=\arg \underset{x}{\max }{a}^k$$
之前我们求minimize用的是gradient descent，那现在我们求Maximum用gradient ascent（梯度上升找最大值）就可以做到这件事了。仔细一想这个方法还是颇为神妙的，因为我们现在是把input x作为要找的参数，对它去用gradient descent或ascent进行update，原来在train CNN的时候，input是固定的，model的参数是要用gradient descent去找出来的；但是现在这个立场是反过来的，在这个task里面model的参数是固定的，我们要用gradient ascent去update这个x，让它可以使degree of activation最大。

上图就是得到的结果，50个filter理论上可以分别找50张image使对应的activation最大，这里仅挑选了其中的12张image作为展示，这些image有一个共同的特征，它们里面都是一些反复出现的某种texture(纹路)，比如说第三张image上布满了小小的斜条纹，这意味着第三个filter的工作就是detect图上有没有斜条纹，要知道现在每个filter检测的都只是图上一个小小的范围而已，所以图中一旦出现一个小小的斜条纹，这个filter就会被activate，相应的output也会比较大，所以如果整张image上布满这种斜条纹的话，这个时候它会最兴奋，filter的activation程度是最大的，相应的output值也会达到最大。

因此每个filter的工作就是去detect某一种pattern，detect某一种线条，上图所示的filter所detect的就是不同角度的线条，所以今天input有不同线条的话，某一个filter会去找到让它兴奋度最高的匹配对象，这个时候它的output就是最大的。我们做完convolution和max pooling之后，会将结果用Flatten展开，然后丢到Fully connected的neural network里面去，之前已经搞清楚了filter是做什么的，那我们也想要知道在这个neural network里的每一个neuron是做什么的，所以就对刚才的做法如法炮制。

我们定义第j个neuron的output就是$a_j$，接下来就用gradient ascent的方法去找一张image x，把它丢到neural network里面就可以让$a_j$的值被maximize，即：
$$x^{\ast }=\arg \underset{x}{\max }{a}^j$$
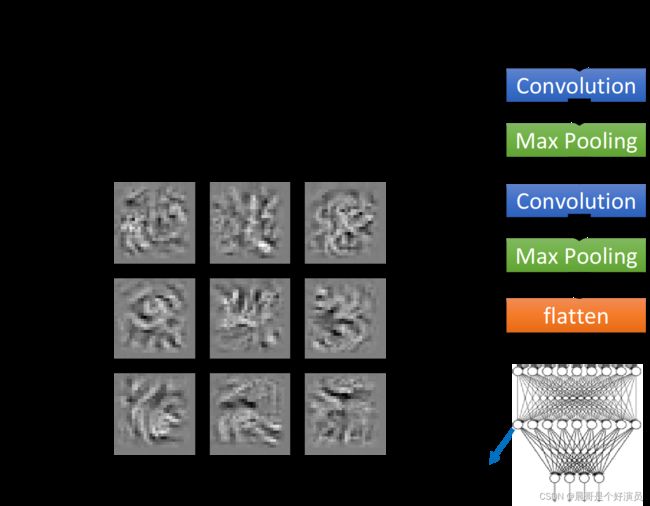
找到的结果如上图所示，同理这里仅取出其中的9张image作为展示，你会发现这9张图跟之前filter所观察到的情形是很不一样的，刚才我们观察到的是「类似纹路的东西」，那是因为每个filter考虑的只是图上一部分的vision，所以它detect的是一种texture；但是在做完Flatten以后，每一个neuron不再是只看整张图的一小部分，它现在的工作是看「整张图」，所以对每一个neuron来说，让它最兴奋的、activation最大的image，不再是texture，而是一个完整的图形，虽然它侦测的不是完整的数字，但是是比较大的pattern。

接下来我们考虑的是CNN的output，由于是手写数字识别的demo，因此这里的output就是10维，我们把某一维拿出来，然后同样去找一张image x，使这个维度的output值最大，即
$$x^{\ast }=\arg \underset{x}{\max }{y}^i$$
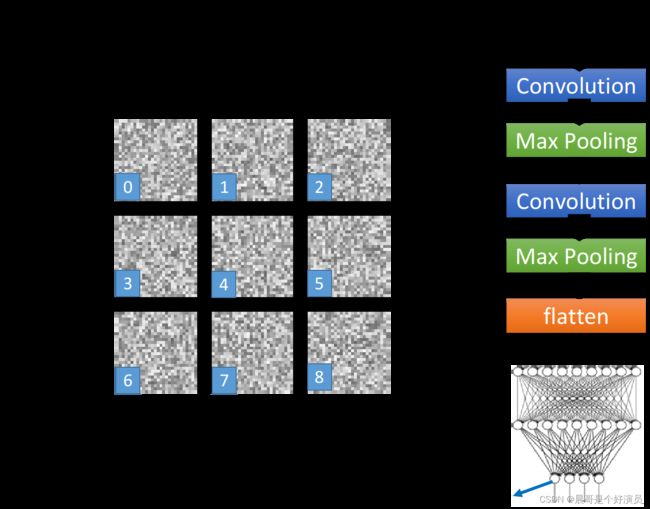
你可以想象既然现在每一个output的每一个dimension就对应到一个数字，那如果我们去找一张image x，它可以让对应到数字1的那个output layer的neuron的output值最大，那这张image显然应该看起来会像是数字1，你甚至可以期待，搞不好用这个方法就可以让machine自动画出数字，但实际上我们得到的结果是这样的，如下图所示：

上面的每一张图分别对应着数字0-8，你会发现，可以让数字1对应neuron的output值最大的image其实长得一点也不像1，就像是电视机坏掉的样子（也有点像二维码的马赛克哈哈），为了验证程序有没有bug，这里又做了一个实验，把上述得到的image真的作为testing data丢到CNN里面，结果classify的结果确实还是认为这些image就对应着数字0-8。所以今天这个neural network，它所学到的东西跟我们人类一般的想象认知是不一样的。

那我们有没有办法，让上面这个图看起来更像数字呢？想法是这样的，我们知道一张图是不是一个数字，它会有一些基本的假设，比如这些image，你不知道它是什么数字，你也会认为它显然就不是一个digit，因为人类手写出来的东西就不是长这个样子的，所以我们要对这个x做一些regularization，我们要对找出来的x做一些constraint，我们应该告诉machine说，虽然有一些x可以让你的y很大，但是它们不是数字，那我们应该加上什么样的constraint呢？最简单的想法是说，画图的时候，白色代表的是有墨水、有笔画的地方，而对于一个digit来说，整张image上涂白的区域是有限的，像上面这些整张图都是白白的，它一定不会是数字。

假设image里的每一个pixel都用$x_{ij}$表示，我们把所有pixel值取绝对值并求和，也就是$\sum _{i,j}|x_{ij}|$，这一项其实就是之前提到过的L1的regularization，再用$y^i$减去这一项，得到：

$$x^{\ast }=\arg \underset{x}{\max }(y^i-\sum _{i,j}|x_{ij}|)$$

这次我们希望再找一个input x，它可以让$y^i$最大的同时，也要让$|x_{ij}|$的summation越小越好，也就是说我们希望找出来的image，大部分的地方是没有涂颜色的，只有少数数字笔画在的地方才有颜色出现，加上这个constraint以后，得到的结果会像下图右侧所示一样，已经隐约有些可以看出来是数字的形状了：

如果再加上一些额外的constraint，比如你希望相邻的pixel是同样的颜色等等，你应该可以得到更好的结果。

以上内容做一个总结就是，卷积神经网络学到的是部分特征，比如图像的某些局部纹理，而卷积后面接一个全连接，这是一个局部到全局的过程，全连接用来学习整体特征。

---

接下来主要罗列一些卷积在图像上的应用。

Deep Dream

其实，这就是Deep Dream的精神，Deep Dream是说，如果你给machine一张image，它会在这个image里面加上它看到的东西，怎么做这件事情呢？你就找一张image丢到CNN里面去，然后你把某一个convolution layer里面的filter或是fully connected layer里的某一个hidden layer的output拿出来，它其实是一个vector；接下来把本来是positive的dimension值调大，negative的dimension值调小，也就是让正的更正，负的更负，然后把它作为新的image的目标，总体来说就是使它们的绝对值变大，然后用gradient descent的方法找一张image x，让它通过这个hidden layer后的output就是你调整后的target，这么做的目的就是，让CNN夸大化它看到的东西——make CNN exaggerates what is sees。

也就是说，如果某个filter有被activate，那你让它被activate的更剧烈，CNN可能本来看到了某一样东西，那现在你就让它看起来更像原来看到的东西，这就是所谓的夸大化。

如果你把上面这张image拿去做Deep Dream的话，你看到的结果就会好像背后有很多怪兽，比如像上图右侧那一只熊，它原来是一个石头，对机器来说，它看这张图的时候，本来就觉得这个石头有点像熊，所以你就更强化这件事，让它看起来真的就变成了一只熊，这个就是Deep Dream。

Deep Style

Deep Dream还有一个进阶的版本，就叫做Deep Style，如果今天你input一张image，Deep Style做的事情就是让machine去修改这张图，让它有另外一张图的风格，如下所示：

实际上机器做出来的效果惊人的好，具体的做法参考reference：A Neural Algorithm of Artistic Style

这里仅讲述Deep Style的大致思路，你把原来的image丢给CNN，得到CNN filter的output，代表这样image里面有什么样的content，然后你把呐喊这张图也丢到CNN里面得到filter的output，注意在这时我们并不在意一个filter output的value到底是什么，我们真正在意的是，filter和filter的output之间的correlation，这个correlation代表了一张image的style。

接下来你就再用一个CNN去找一张image，这张image的content像左边的图片，比如这张image的filter output的value像左边的图片；同时让这张image的style像右边的图片，所谓的style像右边的图片是说，这张image output的filter之间的correlation像右边这张图片。最终你用gradient ascent找到一张image，同时可以maximize左边的content和右边的style，它的样子就像上面图像中左下角所示。

除此之外李宏毅老师在课堂上还罗列了另外的一些应用，比如将CNN应用于围棋、语音辨识（根据语音的频率）以及文本信息提取等，这里就不赘述。