ARMA 时间序列模型
更好的理解协方差以及相关系数
###X因素和Y因素协方差公式:
自相关系数ACF
直观上来说,ACF 描述了一个观测值和另一个观测值之间的自相关,包括直接和间接的相关性信息。
其实自相关系数可以这么理解:把一列数据按照滞后数拆成两列数据,在对这两列数据做类似相关系数的操作。
这组数据是求滞后数为2的自相关系数,则变成求{x1,x2,…,x8}和{x3,x4,…,x10}两者的“相关系数”,相关系数打引号是因为这个相关系数的公式和以往的有点不一样。下面看一下公式的对比:
所以,我们可以这么理解自相关系数, 她就是用来表达一组数据前后数据 (自己和自己) 的相关性的。
PACF 是部分自相关函数或者偏自相关函数。基本上,它不是找到像ACF这样的滞后与当前的相关性,而是找到残差(在去除了之前的滞后已经解释的影响之后仍然存在)与下一个滞后值的相关性。因此,如果残差中有任何可以由下一个滞后建模的隐藏信息,我们可能会获得良好的相关性,并且在建模时我们会将下一个滞后作为特征。请记住,在建模时,我们不想保留太多相互关联的特征,因为这会产生多重共线性问题。因此,我们只需要保留相关功能。
直观上来说,PACF 只描述观测值 y t y_{t} yt 和其滞后项 y t − k y_{t-k} yt−k 之间的直接关系,调整了其他较短滞后项( y t − 1 y_{t-1} yt−1 , y t − 2 y_{t-2} yt−2 …… y t − k − 1 y_{t-k-1} yt−k−1 )的影响。
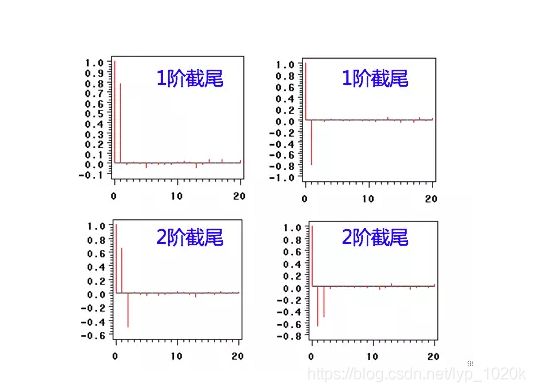
###截尾与拖尾
####拖尾是指序列以指数率单调递减或震荡衰减,而截尾指序列从某个时间点变得非常小。
出现以下情况,通常视为(偏)自相关系数d阶截尾:
在最初的d阶明显大于2倍标准差范围
之后几乎95%的(偏)自相关系数都落在2倍标准差范围以内
且由非零自相关系数衰减为在零附近小值波动的过程非常突然
如果有超过5%的样本(偏)自相关系数都落在两倍标准差范围之外
或者是由显著非0的(偏)自相关系数衰减为小值波动的过程比较缓慢或非常连续
截尾是指时间序列的自相关函数(ACF)或偏自相关函数(PACF)在某阶后均为0的性质(比如AR的PACF);拖尾是ACF或PACF并不在某阶后均为0的性质(比如AR的ACF)。
P 阶AR 过程可以写成下面的式子:
yt=c+ϕ1yt−1+ϕ2yt−2+……+ϕp/yt−p+εt
其中 ε t \varepsilon_{t} εt 是白噪声, y t − 1 y_{t-1} yt−1, y t − 2 y_{t-2} yt−2 是滞后项。阶数P 是滞后值,PACF 曲线在该滞后值首次穿过上限置信区间。这些P 延迟将作为我们预测AR 时间序列的特征。
我们不能在这里使用ACF图,因为即使对于过去很久远的滞后项,它也会显示出良好的相关性。如果我们考虑了这么多特征,我们将遇到多重共线性问题。这对于PACF图来说不是问题,因为它删除了之前滞后已经解释的成分,因此我们只得到了与残差相关的滞后,比如未被较早的滞后项所解释的成分。
###时间序列模型
1.时间序列模型的作用
对未来的资产价格预测
模拟序列
探索金融时间序列的趋势和周期性
时间序列与其他变量的内在关系,为策略提供辅助和增强
不同时间序列之间的关系,发现新的策略
波动率建模,期权相关的策略
白噪声
白噪声是由一组0均值,不变方差,相互独立的元素构成,当然可以对该元素的分布进行假设(如高斯分布)。白噪声如同他的名字听起来一样是杂乱无章的,各元素之间没有任何联系。由白噪声组成的序列是随机游走,随机游走序列的自相关特点是其自相关函数几乎为1并且衰减很慢,这种特征我们称为长记忆性(分形中我们会具体讨论)。
自回归模型(AR模型)
其中,yt是当前值;μ是常数项;p是阶数;γi是自相关系数,ϵt是误差值。
自回归模型是描述当前值与历史值之间的关系的模型,是一种用变量自身的历史事件数据对自身进行预测的方法。
自回归模型的使用有以下四项限制:
该模型用自身的数据进行预测,即建模使用的数据与预测使用的数据是同一组数据;
使用的数据必须具有平稳性;
使用的数据必须有自相关性,如果自相关系数小于0.5,则不宜采用自回归模型;
自回国模型只适用于预测与自身前期相关的现象。
移动平均模型(MA模型)
其中各个字母的意义与AR公式相同,θi为MA公式的相关系数。
移动平均模型关注的是自回归模型中的误差项的累加。它能够有效地消除预测中的随机波动。
自回归移动平均模型(ARMA模型)
在这个公式中,p与q分别为自回归模型与移动平均模型的阶数,是需要人为定义的。γi与θi分别是两个模型的相关系数,是需要求解的。如果原始数据不满足平稳性要求而进行了差分,则为差分自相关移动平均模型(ARIMA),将差分后所得的新数据带入ARMA公式中即可。
###如何用PACF图和ACF图来确定p、q值?
举例
可以看到ACF是一个逐渐趋于0的拖尾,而PACF在7阶过后系数为0,所以模型是AR(7)或AR(8),即ARMA(7,0)或ARMA(8,0)。备选模型ARMA(7,1)。
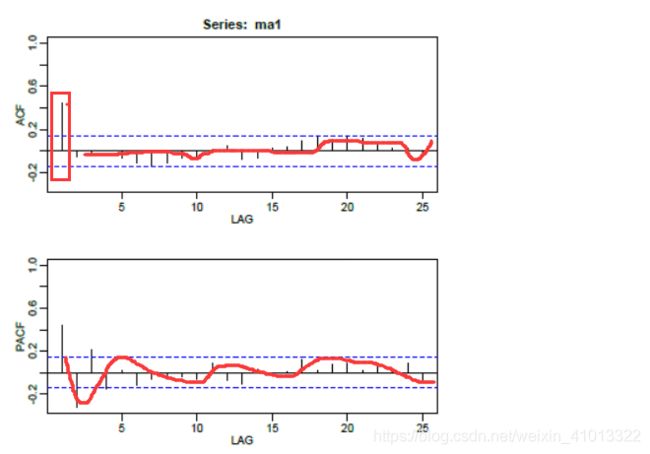
这样的图,可以看到PACF是拖尾,ACF自1阶过后都落在2倍标准差范围内,所以是MA(1)模型。
最后看一个ARMA模型的例子:
ACF和PACF都呈现拖尾,在1阶位置就开始基本落在2倍标准差范围,所以是ARMA(1,1)模型。
ARIMA模型的建模过程:
完全代码:解析版
# statsmodels.tsa.arima_model import ARIMA 导入时序模块
from statsmodels.tsa.arima_model import ARIMA
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import statsmodels.api as sm
from statsmodels.graphics.api import qqplot
# 将list形式转换为矩阵形式
data = [5922, 5308, 5546, 5975, 2704, 1767, 4111, 5542, 4726, 5866, 6183, 3199, 1471, 1325, 6618, 6644, 5337, 7064,
2912, 1456, 4705, 4579, 4990, 4331, 4481, 1813, 1258, 4383, 5451, 5169, 5362, 6259, 3743, 2268, 5397, 5821,
6115, 6631, 6474, 4134, 2728, 5753, 7130, 7860, 6991, 7499, 5301, 2808, 6755, 6658, 7644, 6472, 8680, 6366,
5252, 8223, 8181, 10548, 11823, 14640, 9873, 6613, 14415, 13204, 14982, 9690, 10693, 8276, 4519, 7865, 8137,
10022, 7646, 8749, 5246, 4736, 9705, 7501, 9587, 10078, 9732, 6986, 4385, 8451, 9815, 10894, 10287, 9666, 6072,
5418]
data=pd.Series(data)
# 设置索引
data.index=pd.Index(sm.tsa.datetools.dates_from_range('1901', '1990'))
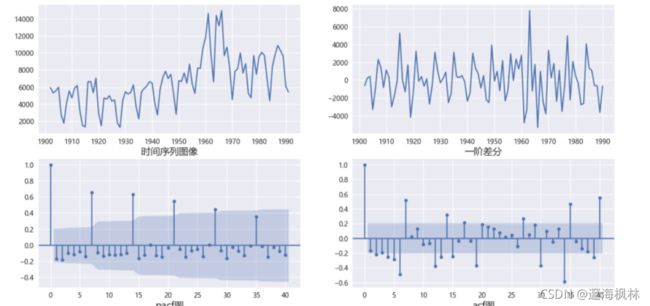
#进行一阶差分
data1=data.diff(1)
data1.dropna(inplace=True)
# 画图部分省略(根据自相关系数图确定适合的模型)
arma_mod1 = sm.tsa.ARMA(data1, (7, 0)).fit()
print(arma_mod1.aic, arma_mod1.bic, arma_mod1.hqic)
arma_mod2 = sm.tsa.ARMA(data1, (7, 1)).fit()
print(arma_mod2.aic, arma_mod2.bic, arma_mod2.hqic)
arma_mod3 = sm.tsa.ARMA(data1, (8, 0)).fit()
print(arma_mod3.aic, arma_mod3.bic, arma_mod3.hqic)
# 找出最适合的模型
# 由上面可以看出ARMA(7,0)模型最佳
# 第四步:进行模型检验
# 首先对ARMA(7,0)模型所产生的残差做自相关图
resid = arma_mod1.resid
# 一定要加上这个变量赋值语句,不然会报错resid is not defined
ax5 = plt.subplot(2, 2, 1)
sm.graphics.tsa.plot_acf(resid.values.squeeze(), lags=40, ax=ax5)
ax6 = plt.subplot(2, 2, 2)
sm.graphics.tsa.plot_pacf(resid, lags=40, ax=ax6)
# 对适合的模型进行自相关(也就是D-W检验)
print(sm.stats.durbin_watson(arma_mod1.resid.values))
# 并观察是否为正态分布
fig = qqplot(resid, line='q', ax=ax7, fit=True)
# 最后用Ljung-Box检验:检验的结果就是看最后一列前十二行的检验概率(一般观察滞后1~12阶),
# 如果检验概率小于给定的显著性水平,比如0.05、0.10等就拒绝原假设,其原假设是相关系数为零。
# 就结果来看,前12阶的P值都是大于0.05,所以在0.05的显著性水平下,不拒绝原假设,即残差为白噪声序列。
r, q, p = sm.tsa.acf(resid.values.squeeze(), qstat=True)
data2 = np.c_[range(1, 41), r[1:], q, p]
table = pd.DataFrame(data2, columns=['lag', 'AC', 'Q', 'Prob(>Q)'])
# 第五步:平稳模型预测,对未来十年进行预测
predict_y = arma_mod1.predict('1990', '2000', dynamic=True)
# print(predict_y)
ax8 = plt.subplot(2, 2, 4)
ax9 = data1.loc['1901':].plot(ax=ax8)
predict_y.plot(ax=ax8)
plt.show()
# 还原到原始序列
ts_restored = pd.Series([data[0]], index=[data.index[0]]).append(data1).cumsum()
# 第六步:使用ARIMA模型进行预测
model = ARIMA(ts_restored, order=(7, 1, 0)) # 导入ARIMA模型
result = model.fit(disp=-1)
# print(result.summary())
result.conf_int() # 模型诊断,可以发现所有的系数置信区间都不为0;即在5%的置信水平下,所有的系数都是显著的,即模型通过检验。
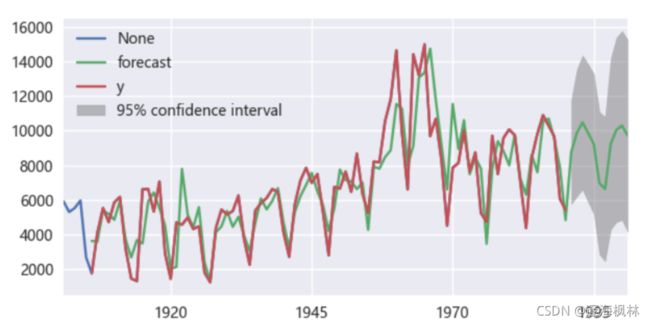
# 最后画出时序图
ax10 = plt.subplot(2, 2, 1)
ax10 = ts_restored.loc['1901':].plot(ax=ax10) # 注意起点是从1901开始
result.plot_predict(5, 100, ax=ax10) # 因为前面是90个数,所以加上预测的10个就是100
plt.show() # 数据预测并画图
效果展示