L1-SVD实现DOA
最近事情太多,来不及更新。看了一篇很经典的论文D. Malioutov, M. Cetin and A. S. Willsky, "A sparse signal reconstruction perspective for source localization with sensor arrays," in IEEE Transactions on Signal Processing, vol. 53, no. 8, pp. 3010-3022, Aug. 2005, doi: 10.1109/TSP.2005.850882. ; 又参考了一个博主“冬瓜班小朋友”的文章https://blog.csdn.net/weixin_38452468/article/details/72879092?spm=1001.2014.3001.5501,受益很大,我在博主的基础上再写一点自己的想法。
1.有关二阶锥问题
锥,建议看下视频https://www.bilibili.com/video/BV1z64y1u7pb/?spm_id_from=333.788.recommend_more_video.-1对凸集,凸锥,仿射集做解释
2.matlab使用cvx工具包
第一次用matlab跑cvx工具包,有点磕磕绊绊,但还好有很多例子可以参考。cvx写matlab有三个步骤,
1)定义变量:常用的变量名,variable:complex(复数),integer(整数),nonnegative(负定),semidefinite(半正定),symmetric(对称矩阵)。 特别需要注意的是我当时写的时候定义了一个中间变量variable,想对其进行赋值,但是总是出现“The following cvx variable(s) have been cleared or overwritten” 错误!后来我才发现想要赋值的中间变量类型应该为expression类型。
2)定义优化函数:minimize( );
3)写约束条件:(<=) or (>=) or (==) 。
https://www.bilibili.com/video/BV1UQ4y1K7Vf?from=search&seid=2817388003776759797视频讲解有关cvx工具包怎么用;比较有帮助
cvx工具包的一般语法如下所示
cvx_begin
define variables; % 定义变量
minimize(objective expression); % 定义优化函数
subject to
constraint1 <= 0; % 定义不等式约束
constraint2 >= 0; % 定义不等式约束
constraint3 == 0; % 定义等式约束
variable == set;
cvx_end
3.有关“A sparse signal reconstruction perspective for source localization with sensor arrays”的内容
1)SVD分解
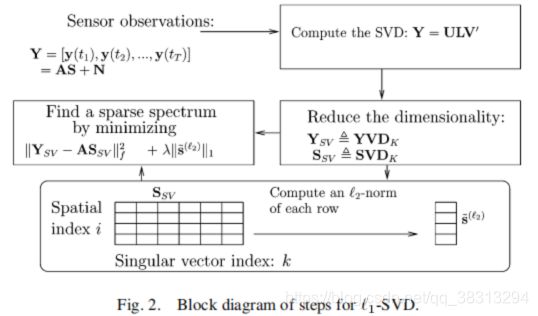
他这里讲得很详细,M:阵元数,K:目标数,T:采样点数,也即快拍数;对Y[M×K维]做SVD分解得到ULV,Dk是T*k维,这样直接相乘能极大减小计算量;文中说到L1-SVD算法的思想是将接收数据分为信号子空间和噪声子空间,如果没有噪声的话,直接用信号子空间的基可以来估计导向矢量A的列的稀疏组合。然后可以将原来的阵列接收模型改写成式(11)的样子,其中Ysv维度是[M×K维],A维度为[M×K维],Ssv维度为[K×K维]。
算法的流程如下图所示
2)二阶锥优化
我凸优化感觉还没有入门,这篇论文里直接用二阶锥来求解式(11)中的问题,我直接懵了。然后找了相关内容https://www.bilibili.com/video/BV1H54y1d75w?from=search&seid=225011787781444983才知道锥和二阶锥的定义和应用。
二阶锥优化是一种非线性优化,可以方便的使用内点法求解问题。
作者将优化问题
改写成二阶锥问题
怎么说呢,这可能就是大佬吧。
在复现的过程中参考博主“冬瓜班小朋友”很多内容,把我的代码也贴在最后,现在总结下来看,只要是理解了算法步骤代码确实不难写。
3)细化网格方法
这篇文章还有一个亮点就是他做了网格细化,我之前在做MUSIC的时候,就想过先进行粗估计再进一步细估计,这样能避免对所有空域搜索,可以极大降低计算量。Dmitry Malioutov的思路就是类似的。等我代码实现了再来share
4)总结
这篇论文里主要是提出了L1范数的惩罚项加强稀疏性;然后对接收信号做SVD分解得到数据量很小的观测模型;并用二阶锥规划方法求解该问题;最后为了进一步减小网格划分的计算量,用了网格细化的方法。
% 作者:gxy
% 功能:复现《A sparse signal reconstruction perspective for source localization with sensor arrays》的方法
% 时间:2021.06.29
clc
clear
close all
% 回波构造
N = 8; % 阵列数
dd = 0.5; % 阵列间距与波长比值
d=0:dd:(N-1)*dd; % 阵列相对波长位置
theta = [-10 5]; % 目标角度
NumK = length(theta);
snr = 10; % 输入信噪比dB
Sample = 20; % 快拍数
A=exp(-1i*2*pi*d.'*sind(theta)); % 导向矢量
S=randn(NumK,Sample); % 目标回波
X=A*S; % 阵列接收信号
X1=awgn(X,snr,'measured'); % 加噪信号
% 构造过完备基
d_lamda = 0.5;
AA=[];
theta=-90:0.5:90;
Ntheta = length(theta);
for kkk= 1:length(theta)
g=exp(-1i*2*pi*[0:N-1]'*d_lamda*sin(theta(kkk)/180*pi));
AA=[AA,g];
end
%% L1-SVD方法
Y = X1;
[U,L,V] = svd(Y) ; % 做SVD分解
Ik = ones(1,NumK);
Dk = [diag(Ik); zeros(NumK,Sample-NumK)']; % 维度T*K维
Ysv = Y*V.'*Dk;
Ssv = S *V.'*Dk;
% 转换为二阶锥规划
% 优化变量为Ssv1
cvx_begin
variables p q;
variable r(Ntheta,1) ;
variable Ssv1(Ntheta,NumK) complex ;
expression sl2(Ntheta,1) ;
minimize(p + 2*q)
subject to
norm(vec(Ysv - AA*Ssv1),2) <=p;
II = ones(Ntheta,1);
II'*r <=q;
for i = 1:Ntheta
norm(Ssv1(i,:),2) <=r(i);
end
cvx_end
Ssv1sum = sum(abs(Ssv1) , 2);
Power_Ssv=10*log10(Ssv1sum/max(Ssv1sum));
plot(theta,Power_Ssv.','r');
xlabel('角度/degree');
ylabel('功率/dB');
grid on;
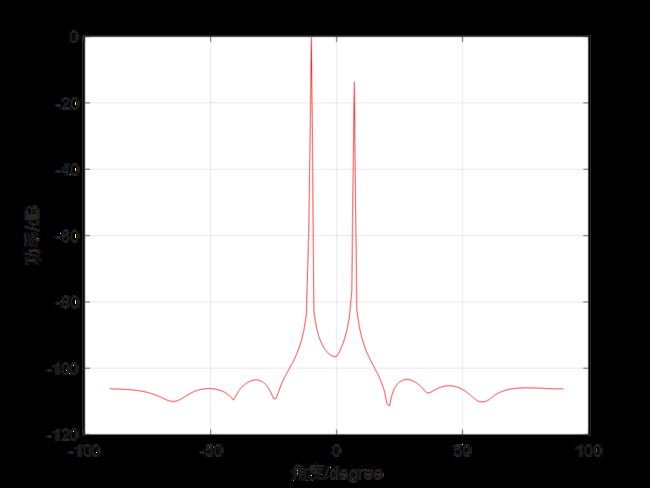
结果如下