EfficientNet 简介
目录
- EfficientNet
-
-
- 网络结构
- MBConv 结构
-
EfficientNet
单独适当增大深度、宽度或分辨率都可以提高网络的精确性,但随着模型的增大,其精度增益却会降低。此外,这三个维度并不是独立的(如:高分辨率图像需要更深的网络来获取更细粒度特征等),需要我们协调和平衡不同尺度的缩放,而不是传统的一维缩放。EfficientNet 的设想就是能否设计一个标准化的卷积网络扩展方法,既可以实现较高的准确率,又可以充分的节省算力资源。其通过 NAS(Neural Architecture Search)技术来搜索网络的图像输入分辨率 r,网络的深度 depth 以及 channel 的宽度 width 三个参数的合理化配置。
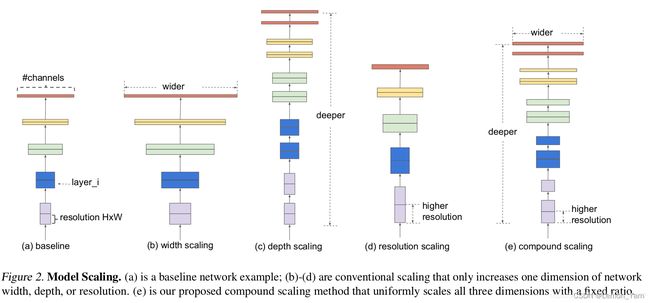
- 增加网络的深度 depth 能够得到更加丰富、复杂的特征并且能够很好的应用到其它任务中。但网络的深度过深会面临梯度消失,训练困难的问题
- 增加网络的 width 够获得更高细粒度的特征并且也更容易训练,但对于 width 很大而深度较浅的网络往往很难学习到更深层次的特征
- 增加输入网络的图像分辨率能够潜在地获得更高细粒度的特征模板,但对于非常高的输入分辨率,准确率的增益也会减小。并且大分辨率图像会增加计算量
第 i 个 层 的 操 作 可 以 看 成 映 射 函 数 : Y i = F i ( X i ) 若 网 络 N 由 k 个 层 组 成 的 , 则 可 表 示 为 : N = F k ⨀ . . . ⨀ F 2 ⨀ F 1 ( X 1 ) = ⨀ j = 1... k F i ( X 1 ) 论 文 中 对 整 个 网 络 的 运 算 进 行 抽 象 : N = ⨀ i = 1... s F i L i ( X < H i , W i , C i > ) \begin{aligned} &第 i 个层的操作可以看成映射函数:Y_i = F_i(X_i) \\ &若网络 N 由 k 个层组成的,则可表示为:N = F_k \bigodot ... \bigodot F_2 \bigodot F_1(X_1) = \bigodot_{j=1...k}F_i(X_1) \\ &论文中对整个网络的运算进行抽象:N = \bigodot_{i=1...s}F_i^{L_i}(X_{
注: F i L i F_i^{L_i} FiLi 表示在 s t a g e ( i ) stage^{(i)} stage(i) 中 F i F_i Fi 被重复执行了 L i L_i Li 次,X 表示输入 s t a g e ( i ) stage^{(i)} stage(i) 的特征矩阵,其维度是 < H i , W i , C i >
为了探究 d, r, w 这三个因子对最终准确率的影响,则将 d, r, w 加入到公式中,我们可以得到抽象化后的优化问题
max d , w , r A c c u r a c y ( N ( d , w , r ) ) s . t . N ( d , w , r ) = ⨀ i = 1... s F i d ⋅ L i ^ ^ ( X < r ⋅ H i ^ , r ⋅ W i ^ , ω ⋅ C i ^ > ) M e m o r y ( N ) ≤ t a r g e t _ m e m o r y F L O P S ( N ) ≤ t a r g e t _ f l o p s \begin{aligned} &\max_{d, w, r}Accuracy(N(d, w, r))\\ &s.t.\quad N(d, w, r) = \bigodot_{i=1...s}\hat{F_i^{d \cdot \hat{L_i}}}(X_{
注:d 用来缩放深度 L i ^ \hat{L_i} Li^; r r r 用来缩放分辨率即影响 H i ^ \hat{H_i} Hi^ 和 W i ^ \hat{W_i} Wi^; ω \omega ω 用来缩放特征矩阵的 channel 即 C i ^ \hat{C_i} Ci^。
接着作者又提出了一个混合缩放方法 ( compound scaling method) 在这个方法中使用了一个混合因子 ϕ 去统一的缩放 width,depth,resolution 参数,具体的计算公式如下:
d e p t h : d = α ϕ w i d t h : w = β ϕ r e s o l u t i o n : r = γ ϕ s . t . α ⋅ β 2 ⋅ γ 2 ≈ 2 α ≥ 1 , β ≥ 1 , γ ≥ 1 \begin{aligned} &depth: d = \alpha^\phi \\ &width: w = \beta^\phi \\ &resolution: r = \gamma^\phi \\ &s.t. \quad \alpha \cdot \beta^2 \cdot \gamma^2 \approx 2 \qquad \alpha \geq1, \beta \geq 1, \gamma \geq 1 \\ \end{aligned} depth:d=αϕwidth:w=βϕresolution:r=γϕs.t.α⋅β2⋅γ2≈2α≥1,β≥1,γ≥1
注:FLOPs(理论计算量)=> depth 翻倍,也翻倍(一次);width 或 resolution 翻倍,则翻四倍(平方)。总的FLOPs倍率可以用近似用 ( α , β 2 , γ 2 ) ϕ (\alpha, \beta^2, \gamma^2)^\phi (α,β2,γ2)ϕ 来表示,当限制 α ⋅ β 2 ⋅ γ 2 ≈ 2 \alpha \cdot \beta^2 \cdot \gamma^2 \approx 2 α⋅β2⋅γ2≈2 时,对于任意一个 ϕ \phi ϕ 而言 FLOPs 相当增加了 2 ϕ 2^{\phi} 2ϕ 倍。对于不同的基准网络搜索出的 α , β , γ \alpha, \beta, \gamma α,β,γ 也不一定相同。
网络结构
下表为EfficientNet-B0的网络框架(B1-B7就是在B0的基础上修改 Resolution、Channels 和 Layers),第一个 Stage 就是一个卷积核大小为 3x3 步距为 2 的普通卷积层(包含 BN 和激活函数 Swish),Stage2~Stage8 都是在重复堆叠 MBConv 结构(最后一列的 Layers 表示该 Stage 重复 MBConv 结构多少次),而 Stage9 由一个普通的 1x1 的卷积层(包含 BN 和激活函数 Swish)、一个平均池化层和一个全连接层组成。表格中每个 MBConv 后会跟一个数字 1 或 6,这里的 1 或 6 就是倍率因子 n 即 MBConv 中第一个 1x1 的卷积层会将输入特征矩阵的 channels 扩充为 n 倍,其中 k3x3 或 k5x5 表示 MBConv 中 Depthwise Conv 所采用的卷积核大小。Channels 表示通过该 Stage 后输出特征矩阵的 Channels。

MBConv 结构

如图所示,MBConv 结构主要由一个 1x1 的普通卷积(升维作用),一个 kxk 的 Depthwise Conv 卷积。k 的具体值主要有 3x3 和 5x5 两种情况,一个 SE 模块,一个 1x1 的普通卷积(降维作用),一个 Droupout 层构成
- 第一个升维的 1x1 卷积层,它的卷积核个数是输入特征矩阵 channel 的 n 倍,n ∈ { 1 , 6 }
- 当 n = 1 时,不要第一个升维的 1x1 卷积层,即 Stage2 中的 MBConv 结构都没有第一个升维的 1x1 卷积层?
- 仅当输入 MBConv 结构的特征矩阵与输出的特征矩阵 shape 相同时才存在 shortcut 连接
- 在源码实现中只有使用 shortcut 的时候才有 Dropout 层
| Model | input_size | width_coefficient | depth_coefficient | drop_connect_rate | dropout_rate |
|---|---|---|---|---|---|
| EfficientNetB0 | 224x224 | 1.0 | 1.0 | 0.2 | 0.2 |
| EfficientNetB1 | 240x240 | 1.0 | 1.1 | 0.2 | 0.2 |
| EfficientNetB2 | 260x260 | 1.1 | 1.2 | 0.2 | 0.3 |
| EfficientNetB3 | 300x300 | 1.2 | 1.4 | 0.2 | 0.3 |
| EfficientNetB4 | 380x380 | 1.4 | 1.8 | 0.2 | 0.4 |
| EfficientNetB5 | 456x456 | 1.6 | 2.2 | 0.2 | 0.4 |
| EfficientNetB6 | 528x528 | 1.8 | 2.6 | 0.2 | 0.5 |
| EfficientNetB7 | 600x600 | 2.0 | 3.1 | 0.2 | 0.5 |
- width_coefficient 代表 channel 维度上的倍率因子,比如在 EfficientNetB0 中 Stage1 的 3x3 卷积层所使用的卷积核个数是 32,那么在 B6 中就是 32 × 1.8 = 57.6,接着取整到离它最近的 8 的整数倍即 56
- depth_coefficient 代表 depth 维度上的倍率因子(仅针对Stage2到Stage8),比如在 EfficientNetB0 中 Stage7 的 \hat{L_i} = 4,那么在 B6 中就是 4 × 2.6 = 10.4 接着向上取整即 11
- drop_connect_rate 是在 MBConv 结构中 dropout 层使用的 drop_rate
- dropout_rate 是最后一个全连接层前的 dropout 层
补充:EfficientNet、EfficientNet网络详解、【一看就懂】EfficientNet详解。凭什么EfficientNet号称当今最强?、Depthwise卷积与Pointwise卷积