3.TransposedConv2d实现 （含dilation）

[C++ 基于Eigen库实现CRN前向推理]

第三部分：TransposedConv2d实现 （含dilation）

• 前言：(Eigen库使用记录)
• 第一部分：WavFile.class (实现读取wav/pcm,实现STFT)
• 第二部分：Conv2d实现
• 第三部分：TransposedConv2d实现 (mimo,padding,stride,dilation,kernel,outpadding)
• 第四部分：NonLinearity （Sigmoid，Tanh，ReLU，ELU，Softplus）
• 第五部分：LSTM

1. TransposedConv2d介绍

原先一直不明确反卷积具体是怎么操作的，查了一些资料发现反卷积其实是由卷积实现的。
先来看一个简单示例，这是一个input=(2,2),kernel=(3,3), no padding, no strides（即为1）的反卷积。
可以发现，反卷积其实就是通过在输入上进行零填充，再进行普通卷积达到上采样的目的。
那如何填充，由padding,stride和dilation决定，我们一步步考虑。

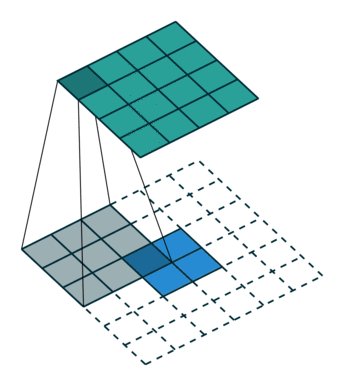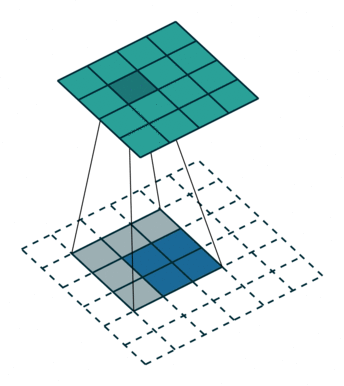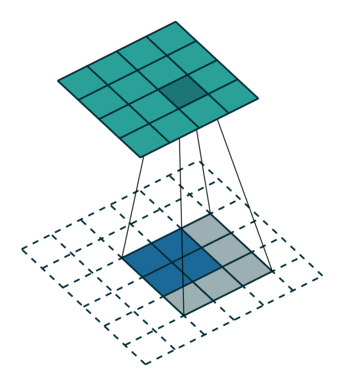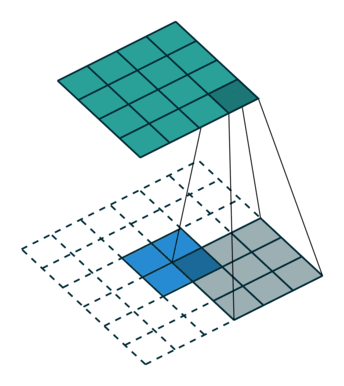
1.1 反卷积的Padding参数

在传统卷积中，我们的 padding 范围为 [0, k − 1] ，p = 0 被称为 No padding，p = k − 1被称为 Full Padding。
而在反卷积中的 p ′ 刚好相反，也就是 p ′ = k − 1 − p
也就是当我们传p=0时，实际上反卷积的padding_size = k - 1, 传p=k-1时，padding_size = 0

如上图，p=0 ===> 则在TransposedConv中p ’ = 3-1-0 = 2,在外圈填充了2圈0
输入(2,2)的输出尺寸称为(4,4)，达到上采样的效果。

1.2 反卷积的Stride参数

在反卷积中，Stride其实不是跳步的含义，具体的操作是在两个相邻行或列之间填充stride-1个0。
比如下图为input=(2,2),kernel=(3,3) stride=(2,2),padding=(0,0)时的示意图：

但在反卷积中，实际的stride都是1，所以上述情况下，输出map大小为(5,5)

1.3 反卷积中的output_padding参数

output_padding参数也是在数据边缘填充数据，与padding不同的是，padding是在输入图上进行填充，再进行卷积操作。
而output_padding是对卷积操作后的结果进行填充。

使用目的：为了补偿由卷积-反卷积操作中造成的维度损失。如图在8*8的图上进行卷积时，其实最右边和最下边的一行是没有参与卷积运算的，这是因为stride为2，再走2步就超出图片范围了。所以7x7和8x8最终的结果都为3x3。而反卷积的时候默认恢复成7×7，由此造成了一个维度的损失。

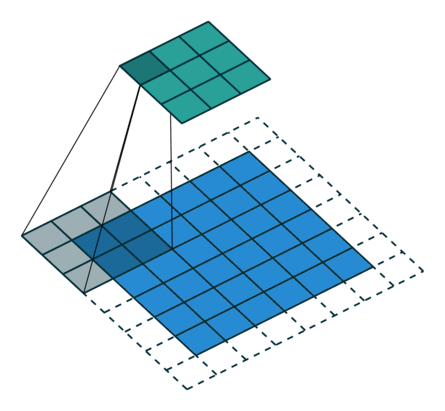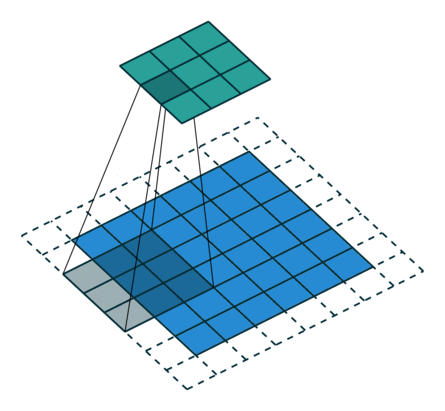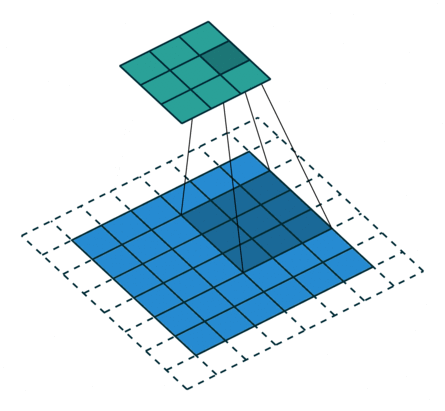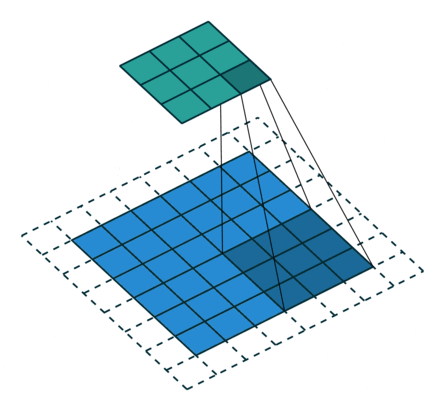
那么如果我们想让3x3的反卷积得8x8而不是7x7，那么我们就需要在输出图片边缘补充数据，具体补几行就是output_padding指定的。所以output_padding的作用就是：在输出图像右侧和下侧补值，用于弥补stride大于1带来的缺失。其中output_stadding必须小于stride。

我们拿pytorch的代码测试一下：

	input = torch.arange(1, 10).reshape(1, 1, 3, 3).float()
    kernel = torch.ones(1, 1, 2, 3).float()
    bias = torch.randn(1).float()
	th_out = F.conv_transpose2d(input, kernel, bias, stride=(2, 2), padding=(0, 1), dilation=(1, 1),
                                output_padding=(1, 1))
	print(input)
    print(kernel)
    print(th_out)
    

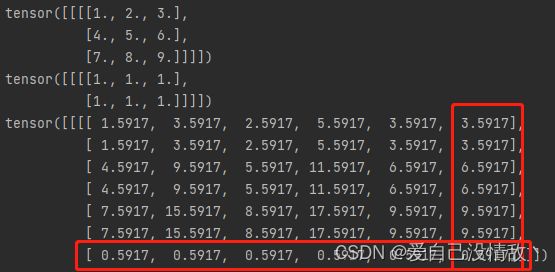
可以看到，pytorch的反卷积在进行output_padding的时候，并不是进行零填充，在行方向应用的是bias（图中为0.5917），在列方向应用为卷积最后的最后一列的复制。

1.4 反卷积中的dilation参数

网络上大部分的资料都是带洞（正）卷积，一直不清楚反卷积中的dilation是怎么进行填充的。
我们拿pytorch做一个带洞反卷积的测试，我们用input(3,3)，kernel(2,2)进行反卷积：

	input = torch.arange(1, 10).reshape(1, 1, 3, 3).float()
    kernel = torch.ones(1, 1, 2, 2).float()
    bias = torch.zeros(1).float()
	th_out = F.conv_transpose2d(input, kernel, bias, stride=(1, 1), padding=(0, 0), dilation=(1, 2))
	print(input)
    print(kernel)
    print(th_out)

正常情况下，如果不带洞，按照前面两小结的结论，输出应该是

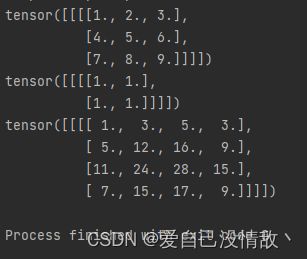
但在列方向使dilation=2之后，发现输出变为

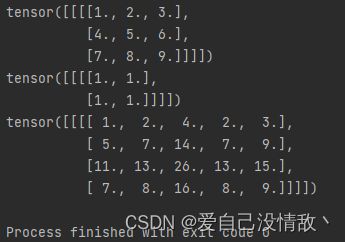
发现多了长度变长了1,事实上，一个为kernel的卷积核，在进行dilation卷积的时候，对输入图的切片范围会变为(kernel-1)dilation+1,具体可以看图。考虑到反卷积是对输入图的填充，在输入图前后各填充 (kernel - 1) * (dilation - 1)的零。

所以对输入图填充后输入和输出分别为，这里是我用实现的C++版本输出的,input=(3,3),kernel=(3,3),stride=(1,2),dilation=(1,2),padding=(0,1)。
行方向：可以看到所有的pad形式，红色标出的是行方向的填充，这里padding[0]=0，则实际的填充数为kernel[0]-1-0=2,其次dilation=1，stride=1,没有额外的填充，所以总共就是上下各2行。
列方向：padding[1]=1，所以实际的填充数为kernel[1]-1-1 =1,即为左右蓝色的两列。另外stride[1]=2，则在每个元素间填充stride[1]-1列，即为中间标为绿色的列。最后dilation[1]=2，则两边分别填充(kernel[1]-1)(dilation[1]-1)列，即各填充2*1列，如黄色所示。
填充完毕后，就可以进行stride=(1,1),dilation=(1,2)的正卷积。

0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 1 0 2 0 3 0 0 0
0 0 0 4 0 5 0 6 0 0 0
0 0 0 7 0 8 0 9 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0

0 3 0 6 0 5 0
0 12 0 21 0 16 0
0 27 0 45 0 33 0
0 24 0 39 0 28 0
0 15 0 24 0 17 0

2. 基于Eigen的C++实现

2.1 Layer_TransposedConv2d.h

//
// Created by Koer on 2022/10/31.
//

#ifndef CRN_LAYER_TRANSPOSEDCONV2D_H
#define CRN_LAYER_TRANSPOSEDCONV2D_H

#include "tuple"
#include "mat.h"
#include "Eigen/CXX11/Tensor"

class Layer_TransposedConv2d {
public:
    Layer_TransposedConv2d();

    Layer_TransposedConv2d(int64_t in_ch, int64_t out_ch, std::pair<int64_t, int64_t> kernel = std::make_pair(1, 1),
                           std::pair<int64_t, int64_t> stride = std::make_pair(1, 1),
                           std::pair<int64_t, int64_t> dilation = std::make_pair(1, 1),
                           std::pair<int64_t, int64_t> padding = std::make_pair(0, 0),
                           std::pair<int64_t, int64_t> out_padding = std::make_pair(0, 0));

    void LoadState(MATFile *pmFile, std::string state_preffix);

    Eigen::Tensor<float_t, 4> forward(Eigen::Tensor<float_t, 4> &input);

private:
    int64_t in_channels;
    int64_t out_channels;
    std::pair<int64_t, int64_t> kernel_size;
    std::pair<int64_t, int64_t> stride;
    std::pair<int64_t, int64_t> dilation;
    std::pair<int64_t, int64_t> padding;
    std::pair<int64_t, int64_t> out_padding;
    Eigen::Tensor<float_t, 4> weights;
    Eigen::Tensor<float_t, 2> bias;
};


#endif //CRN_LAYER_TRANSPOSEDCONV2D_H

2.1 Layer_TransposedConv2d.cpp

//
// Created by Koer on 2022/10/31.
//

#include "iostream"
#include "../include/Layer_TransposedConv2d.h"

Layer_TransposedConv2d::Layer_TransposedConv2d() {
    this->in_channels = 1;
    this->out_channels = 1;
    this->kernel_size = std::make_pair(1, 1);
    this->stride = std::make_pair(1, 1);
    this->padding = std::make_pair(0, 0);
    this->out_padding = std::make_pair(0, 0);
}

Layer_TransposedConv2d::Layer_TransposedConv2d(int64_t in_ch, int64_t out_ch, std::pair<int64_t, int64_t> kernel,
                                               std::pair<int64_t, int64_t> stride, std::pair<int64_t, int64_t> dilation,
                                               std::pair<int64_t, int64_t> padding,
                                               std::pair<int64_t, int64_t> out_padding) {
    /* code */
    this->in_channels = in_ch;
    this->out_channels = out_ch;
    this->kernel_size = kernel;
    this->stride = stride;
    this->dilation = dilation;
    this->padding = padding;
    this->out_padding = out_padding;
}

void Layer_TransposedConv2d::LoadState(MATFile *pmFile, std::string state_preffix) {
    std::string weight_name = state_preffix + "_weight";
    std::string bias_name = state_preffix + "_bias";

    // Read weight
    mxArray *pa = matGetVariable(pmFile, weight_name.c_str());
    auto *values = (float_t *) mxGetData(pa);
    // First Dimension  eg.(16,1,2,3)  ===> M=16
    long long dim1 = mxGetM(pa);
    // Rest Total Dimension eg.(16,1,2,3) ===>N = 1 * 2 * 3 = 6
    long long dim2 = mxGetN(pa);
    dim2 = dim2 / this->kernel_size.first / this->kernel_size.second;
    this->weights.resize(dim1, dim2, this->kernel_size.first, this->kernel_size.second);
    int idx = 0;
    // 因为是列优先，所以倒序嵌套循环
    for (int i = 0; i < this->kernel_size.second; i++) {
        for (int j = 0; j < this->kernel_size.first; j++) {
            for (int k = 0; k < dim2; k++) {
                for (int l = 0; l < dim1; l++) {
                    this->weights(l, k, j, i) = values[idx++];
                }
            }
        }
    }
    // std::cout << this->weights << std::endl;

    // Read bias
    pa = matGetVariable(pmFile, bias_name.c_str());
    values = (float_t *) mxGetData(pa);
    dim1 = mxGetM(pa);
    dim2 = mxGetN(pa);
    this->bias.resize(dim1, dim2);
    idx = 0;
    for (int i = 0; i < dim2; i++) {
        for (int j = 0; j < dim1; j++) {
            this->bias(j, i) = values[idx++];
        }
    }
    // std::cout << this->bias << std::endl;
    std::cout << " Finish Loading State of " + state_preffix << std::endl;
}

Eigen::Tensor<float_t, 4> Layer_TransposedConv2d::forward(Eigen::Tensor<float_t, 4> &input) {
    const Eigen::Tensor<size_t, 4>::Dimensions &dim_inp = input.dimensions();
    std::pair<int64_t, int64_t> trans_padding = std::make_pair(this->kernel_size.first - 1 - this->padding.first,
                                                               this->kernel_size.second - 1 - this->padding.second);
    // pad大小包含在输入每个点之间插入strid-1个0，在首尾各插入pad个0，以及在首尾各插入(K-1)*(D-1)个0
    int64_t pad_size_time = trans_padding.first + (this->kernel_size.first - 1) * (this->dilation.first - 1);
    int64_t pad_size_freq = trans_padding.second + (this->kernel_size.second - 1) * (this->dilation.second - 1);
    int64_t batch = dim_inp[0], C_in = dim_inp[1], H_in = dim_inp[2], W_in = dim_inp[3];
    int64_t H_pad = H_in + pad_size_time * 2 + (H_in - 1) * (this->stride.first - 1);
    int64_t W_pad = W_in + pad_size_freq * 2 + (W_in - 1) * (this->stride.second - 1);

    /* padding tensor */
    // 这里应该可以用pad函数，但是我不会，input.pad返回的是一个Op，不能赋值到Tensor4变量，有懂哥可以交流一下
    Eigen::Tensor<float_t, 4> padded_input = Eigen::Tensor<float_t, 4>(batch, C_in, H_pad, W_pad);
    padded_input.setZero();
    padded_input.stridedSlice(
            Eigen::array<int64_t, 4>{0, 0, pad_size_time, pad_size_freq},
            Eigen::array<int64_t, 4>{batch, this->in_channels, H_pad - pad_size_time, W_pad - pad_size_freq},
            Eigen::array<int64_t, 4>{1, 1, this->stride.first, this->stride.second}) = input;

    /* output shape */
    int64_t H_out = (H_in - 1) * this->stride.first - 2 * this->padding.first +
                    this->dilation.first * (this->kernel_size.first - 1) +
                    this->out_padding.first + 1;
    int64_t W_out = (H_in - 1) * this->stride.second - 2 * this->padding.second +
                    this->dilation.second * (this->kernel_size.second - 1) +
                    this->out_padding.second + 1;
    Eigen::Tensor<float_t, 4> output = Eigen::Tensor<float_t, 4>(batch, out_channels, H_out, W_out);
    output.setZero();


    Eigen::Tensor<float_t, 4> region;
    Eigen::Tensor<float_t, 4> kernel;
    Eigen::Tensor<float_t, 1> tmp_res;
    Eigen::array<int, 3> dim_sum{1, 2, 3};
    int32_t h_region = (this->kernel_size.first - 1) * this->dilation.first;
    int32_t w_region = (this->kernel_size.second - 1) * this->dilation.second;
    for (int32_t idx_batch = 0; idx_batch < batch; idx_batch++) {
        for (int32_t idx_outc = 0; idx_outc < this->out_channels; idx_outc++) {
            kernel = this->weights.slice(Eigen::array<int32_t, 4>{idx_outc, 0, 0, 0},
                                         Eigen::array<int32_t, 4>{1, this->in_channels, this->kernel_size.first,
                                                                  this->kernel_size.second}
            );
            for (int32_t idx_h = 0; idx_h < H_pad - h_region; idx_h++) {
                for (int32_t idx_w = 0; idx_w < W_pad - w_region; idx_w++) {
                    region = padded_input.stridedSlice(
                            Eigen::array<int64_t, 4>{idx_batch, 0, idx_h, idx_w},
                            Eigen::array<int64_t, 4>{idx_batch + 1, this->in_channels, idx_h + h_region + 1,
                                                     idx_w + w_region + 1},
                            Eigen::array<int64_t, 4>{1, 1, this->dilation.first, this->dilation.second});
                    tmp_res = (region * kernel).sum(dim_sum);
                    output(idx_batch, idx_outc, idx_h, idx_w) = tmp_res(0) + this->bias(0, idx_outc);
                }
            }
        }
    }
    /* set out_padding value, rows = bias, cols = cols[-1] */

    if (this->out_padding.first > 0 && this->out_padding.first < this->stride.first) {
        for (int64_t idx_batch = 0; idx_batch < batch; idx_batch++) {
            for (int64_t idx_outc = 0; idx_outc < this->out_channels; idx_outc++) {
                for (int64_t idx_h = H_out - this->out_padding.first; idx_h < H_out; idx_h++) {
                    for (int64_t idx_w = 0; idx_w < W_out; idx_w++) {
                        output(idx_batch, idx_outc, idx_h, idx_w) = this->bias(0, idx_outc);
                    }
                }
            }
        }
    }
    if (this->out_padding.second > 0 && this->out_padding.second < this->stride.second) {
        for (int64_t idx_batch = 0; idx_batch < batch; idx_batch++) {
            for (int64_t idx_outc = 0; idx_outc < this->out_channels; idx_outc++) {
                for (int64_t idx_h = 0; idx_h < H_out; idx_h++) {
                    for (int64_t idx_w = W_out - this->out_padding.second; idx_w < W_out; idx_w++) {
                        output(idx_batch, idx_outc, idx_h, idx_w) = output(idx_batch, idx_outc, idx_h, idx_w - 1);
                    }
                }
            }
        }
    }

    return output;
}

C++很久没有写过了，代码可能有些冗余，有错误的地方欢迎大家指正~

参考链接：
[1] 反卷积通俗详细解析与nn.ConvTranspose2d重要参数解释
[2] Github卷积动图