图像特征总结(二)
图像特征总结(二)
- 1.Histogram(直方图)特征
-
- 1.1 直方图均衡化
- 1.2 直方图规定化
- 2.3 例子
- 2. GLCM(灰度共生矩阵)
-
- 2.1GLCM原理
- 3 Color(颜色空间转换)
-
- 3.1 颜色空间
-
- 3.1.1 RGB
- 3.1.2 HSV
- 3.1.3 LAB
- 3.1.4 GRAY(灰度变换)
- 4. HOG
-
- 4.1 原理
- 参考资料链接
1.Histogram(直方图)特征
灰度直方图是最简单、有用的工具之一。从对图像的分析与观察,直到形成一个有效的处理方法,都离不开直方图。
直方图:表示数字图像中每一灰度级像素出现的频次(该灰度级的像素数目)。
p ( k ) = n k p(k) = n_k p(k)=nk, n k n_k nk是图像中第k个灰度级的像素总数。或者 p ( r k ) = n k n p(r_k) = \frac{n_k}{n} p(rk)=nnk,n是图像的像素总数。

上图中,横坐标是灰度等级,纵坐标是各个像素的个数。
直方图性质:
- 无空间信息
- 直方图与图像存在一对多的关系,即不同的图像有可能包含相同的直方图。
- 可叠加性(全图与子图),即原图像可由多个子图像叠加而成。


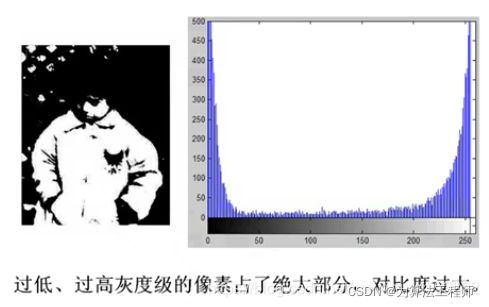
直方图反映了图像的清晰程度。当直方图均匀分布时,图像最清晰。因此,可以通过查看是否合理地利用了全部被允许地灰度级来判断一幅图像是否清晰。即,一幅图像应该尽可能地利用全部可能地灰度级。
import cv2
import numpy as np
def calcAndDrawHist(image, color):
hist = cv2.calcHist([image], [0], None, [256], [0.0, 255.0])
minVal, maxVal, minLoc, maxLoc = cv2.minMaxLoc(hist)
histImg = np.zeros([256, 256, 3], np.uint8)
hpt = int(0.9 * 256);
for h in range(256):
intensity = int(hist[h] * hpt / maxVal)
cv2.line(histImg, (h, 256), (h, 256 - intensity), color)
return histImg
1.1 直方图均衡化
直方图修正:通过灰度映射函数 G n e w = T ( G o l d ) G_{new} = T(G_{old}) Gnew=T(Gold),将原灰度直方图改造成所希望的直方图。
直方图均衡化是一种最常用的直方图修正,它把给定图像的直方图分布改造成均匀直方图分布(杂乱 → \to →均匀)。
均衡化后吗,图像直方图是平直的。即各灰度级具有相同的出现频次,或者说各灰度级具有均匀的概率分布。因此,图像看起来更加清晰(图像增强)。
直方图均衡化灰度映射函数:
-
连续灰度级的情况
P ( r ) P(r) P(r)代表概率密度函数; o ( 黑 ) ≤ r ≤ I ( 白 ) o(黑) \leq r \leq I(白) o(黑)≤r≤I(白) ,代表灰度级。 r r r值归一化,最大灰度值为1。


考虑到灰度变换不影响像素的位置分布,也不会增减像素数目。那么有:
∫ 0 r p ( r ) d r = ∫ 0 s p ( s ) d s = ∫ 0 s 1 d s = s = T ( r ) T ( r ) = ∫ 0 r p ( r ) d r \int_{0}^{r} p(r)\, {\rm d}r = \int_{0}^{s} p(s)\, {\rm d}s = \int_{0}^{s} 1\, {\rm d}s = s = T(r) \\ T(r) = \int_{0}^{r} p(r)\, {\rm d}r ∫0rp(r)dr=∫0sp(s)ds=∫0s1ds=s=T(r)T(r)=∫0rp(r)dr
T ( r ) T(r) T(r)为累计分布函数。
因为目标函数是均匀的,所以 P ( s ) = 1 P(s) = 1 P(s)=1。这是因为哪个像素的个数必定不为0. -
数字图像的直方图均衡化
设一幅数字图像的像素总数为 n n n,分为 L L L个灰度级。那么,第 k k k个灰度级出现的概率 P ( r k ) = n k / n P(r_k) = n_k / n P(rk)=nk/n, n k n_k nk表示第k个灰度级出现的频数,其中, 0 ≤ r k ≤ 1 , k = 0 , 1 , 2 , … , L − 1 0 \leq r_k \leq 1, \quad k = 0,1,2, \dots ,L-1 0≤rk≤1,k=0,1,2,…,L−1
那么,第k个灰度级的累计分布函数为:
s k = T ( r k ) = ∑ j = 0 k p ( r j ) = ∑ j = 0 k n j n s_k = T(r_k) = \sum_{j=0}^k p(r_j) = \sum_{j=0}^k \frac{n_j}{n} sk=T(rk)=j=0∑kp(rj)=j=0∑knnj



可以看见均衡化后的图片天空出现了伪轮廓,因为变化时几个等级的灰度均衡化到一个灰度,另外几个灰度又均衡化到了另一个灰度,就会出现灰度差异明显的情况,即灰度的不连续变化,造成了天空的伪轮廓。
1.2 直方图规定化
修改一幅图像的直方图,使得它与另一幅图像的直方图匹配或具有一种预先规定的函数形状。目标:突出感兴趣的灰度范围,使图像质量改善。
2.3 例子
- 将图像转换成负片效果(反变换)
# -*- coding:utf-8
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
img2 = np.zeros((256,256,3), np.uint8)#无符号八位整型,表示范围是[0, 255]的整数
img1 = cv.imread("/home/image/Pictures/lena256.jpg")#默认读取三通道
img2[:] = 255 - img1[:]#负片效果,对整个区间进行运算时,不用把三个:全写上,写一个也行
imgcolor = cv.imread("/home/image/Pictures/bottle.png")
print(imgcolor.shape)
imgtemp = np.zeros((imgcolor.shape[0],imgcolor.shape[1],3),np.uint8)#不知道图片的尺寸时调用shape来初始化
(b,g,r) = cv.split(imgcolor)#CV是bgr的顺序,要转化成matplotlib的rgb顺序
imgcolor= cv.merge((r,g,b))
imgtemp[:,:,:] = 255 -imgcolor[:,:,:]
img =[img1,img2,imgcolor,imgtemp]
titles =['256-gary image','oppsite image','24-bit image ','opposite image']
for i in range(4):
plt.subplot(1,4,i+1)
plt.imshow(img[i])
plt.yticks()
plt.xticks()
plt.title(titles[i])
plt.show()
dst = cv2.addWeighted(src1, alpha, src2, beta,gamma, dst, dtype)
该函数的功能是将两个图像进行加权融合,每个像素点的像素是两种源图像 ( s r c 1 , s r c 2 ) (src_1, src_2) (src1,src2)对应的像素点的像素加权算出来的,融合公式如下:
d s t = α ∗ s r c 1 + β ∗ s r c 2 + γ dst = \alpha *src_1 + \beta * src_2 + \gamma dst=α∗src1+β∗src2+γ
参数:
- src1:插入的第一个图片;
- src2:插入的第二个图片;
- alpha:double类型,加权系数,是src1图片的融合占比 ;
- beta:double类型,加权系数,是src2图片的融合占比;
- gamma:double类型,加权后图像的偏移量;
- dst:输出图像;
- dtype:默认为-1。
# -*- coding:utf-8
# opencv read image is BGR channel,and matplot read is RGB
import cv2 as cv
from matplotlib import pyplot as plt
import numpy as np
# two images addweighted and simple add
imglena = cv.imread("/home/image/Pictures/lena512color.jpg")
(r,g,b)= cv.split(imglena)
img1 = cv.merge([b,g,r])#转换成rgb通道顺序
imgbaboon = cv.imread("/home/image/Pictures/baboon.jpg")
(r,g,b)= cv.split(imgbaboon)
img2 = cv.merge([b,g,r])
#相加的两个图片尺寸必须一致
img3 = cv.addWeighted(img1,0.6,img2,0.4,gamma=0)#第一幅图的权重是0.6,第二幅图的权重是0.4,偏移量为0
img4 = np.zeros(img3.shape,np.uint8)
img4[:,:,:] = img1[:,:,:] + img2[:,:,:]
images = [img1,img2,img3,img4]
titles = ['lena','baboon','maxture Image',' simple + Image']
for i in range(4):
plt.subplot(2,2,i+1),plt.imshow(images[i],cmap='gray')#cmap就是调色板
plt.title(titles[i])
plt.xticks([]),plt.yticks([])
plt.show()
# -*- coding:utf-8
# opencv read image is BGR channel,and matplot read is RGB
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
names = "/home/image/Pictures/lena.jpg"
img = cv.imread(names,0)
(H,W)=img.shape#高(垂直长度),宽(水平长度)
pixel = H * W
def display(files):
cv.namedWindow("hist-imgs", 0)
cv.resizeWindow("hist-imgs",3*W,H)
cv.imshow("hist-imgs", np.hstack(files))
def opencvdef(img):
# opencv own's equlization function
t1 = cv.getTickCount()
eq = cv.equalizeHist(img)#cv的直方图均衡函数
t2 = cv.getTickCount()
T1 = (t2 - t1) / cv.getTickFrequency()
print("Opencv Histogram() Time consuming is ", T1,'second')
files.append(eq)#加入列表
#手动均衡化
def own(img):
# bins is gray volume ,wide 0~255 ,hist is every gray volume numbers
t1 =cv.getTickCount()
hist,bins = np.histogram(img.flatten(), 256, [0, 255])
LUT = np.zeros(256,np.uint8)
LUT[0] =1.0 *hist[0] / pixel *255
sumnums = hist[0]
for i in range(1,256):
#s[i]= sum of gray form 0 to i
sumnums =sumnums +hist[i]
# LUT is equliztion array = (255 X s[i])
LUT[i] = np.uint8(1.0*sumnums /pixel *255)
temps =np.zeros((H,W),np.uint8)
for i in range(H ):
for j in range(W ):
temps[i,j] =LUT[img[i,j]]
t2 = cv.getTickCount()
T2 = (t2 - t1) / cv.getTickFrequency()
print("Own Histogram() Time consuming is ", T2,'second')
files.append(temps)
pltshow(files)
display(files)
cv.waitKey(0)
def pltshow(files):
for i in range(3):
plt.subplot(2,3,i+1),plt.imshow(files[i], cmap='gray', interpolation='bicubic')
plt.xticks([]),plt.yticks([])#remove 刻度
for i in range(3):
hist, bins = np.histogram(files[i].flatten(), 256, [0, 255])
plt.subplot(2,3,4+i)
#flatten()将图像展开成一维数组
plt.hist(files[i].flatten(),bins=256,range=[0,255],color='red')
plt.xlim(0, 255),plt.ylim(0, hist.max()+1)#坐标轴范围,hist.max()即为所有像素的频数中最大的一个
plt.show()
if __name__ == '__main__':
files =[img]
opencvdef(img)
own(img)
# -*- coding:utf-8
# opencv read image is BGR channel,and matplot read is RGB
import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
# Display image histogram
def showHist(src,name):
plt.hist(src.ravel(), 256, [0, 256])
plt.xlim(0, 255)
plt.xlabel('DN'), plt.ylabel('count')
plt.title(name+' histogram')
plt.show()
return
# Statistical image Cumulative frequency(累加频数)
def cumFre(src):
# get image size
rows, cols = src.shape
# get image histogram like (hist,bins = np.histogram(img.flatten(), 256, [0, 255]))等效
hist = cv.calcHist([src], [0], None, [256], [0, 256])#频数
# get image hist_add is formula si
cumHist = np.cumsum(hist)#累加频数
# Calculation of cumulative frequency of images
cumf = cumHist / (rows*cols)
return cumf
# Histogram equalization
def histEq(src):
rows, cols = src.shape
hist = cv.calcHist([src], [0], None, [256], [0, 256])
cumHist = np.cumsum(hist)
LUT = np.zeros(256, np.float32) #gary search sheet
for i in range(256):
LUT[i] = 255.0/(rows*cols) * cumHist[i]
LUT = np.uint8(LUT + 0.5)
dst = cv.LUT(src, LUT) # search sheet
return dst
# Histogram matching (image to be matched, reference image)
def histMatching(oriImage, refImage):
oriCumHist = cumFre(oriImage) #
refCumHist = cumFre(refImage) #
lut = np.ones(256, dtype = np.uint8) * (256-1) #new search sheet
start = 0
for i in range(256-1):
temp = (refCumHist[i+1] - refCumHist[i]) / 2.0 + refCumHist[i]
for j in range(start, 256):
if oriCumHist[j] <= temp:
lut[j] = i
else:
start = j
break
dst = cv.LUT(oriImage, lut)
return dst
if __name__ == '__main__':
# Using this image histogram as a normalization template(规定化模板)
refImg = cv.imread('/home/image/Pictures/house128.jpg', 0)
# This is a original image
oriImg = cv.imread('/home/image/Pictures/lena.jpg',0)
showHist(refImg,'refImg')
showHist(oriImg,'oriImg')
# def function to nomaliztion
outImg = histMatching(oriImg, refImg)
cv.imshow('original-Img is lena', oriImg)
cv.namedWindow('reference- Img is house',cv.WINDOW_AUTOSIZE)
cv.resizeWindow('reference- Img is house',(2*refImg.shape[0],2*refImg.shape[1]))
cv.imshow('reference- Img is house', refImg)
cv.imshow('output lena Img', outImg)
cv.waitKey(0)
cv.destroyAllWindows()
2. GLCM(灰度共生矩阵)
2.1GLCM原理
GLCM,即灰度共生矩阵,是一个 L ∗ L L*L L∗L的方阵, L L L为源图像的灰度级。
GLCM的含义:描述的是具有某种空间位置关系的两个像素的联合分布,可以看成两个像素灰度对的联合直方图,是一种二阶统计方法。
两个像素常见的空间位置关系有:垂直、水平、正负45°,共四种。
常用的GLCM特征:
-
能量:表示灰度共生矩阵元素值的平方和,反映了图像灰度分布均匀程度和纹理粗细程度。
如果GLCM中所有值均相等,则ASM值小;相反,如果其中一些值大而其它值小,则ASM值大。
当共生矩阵元素集中分布时,此时ASM值大。ASM值大表明一种较均一和规则变化的纹理模式 -
对比度:反映了图像的清晰度和纹理深浅的程度。纹理沟纹越深,其对比度越大,视觉效果越清晰。
反之,对比度小,则纹理沟纹浅,视觉效果模糊。灰度差:对比度大的像素对越多,这个值(灰度差)越大。
GLCM中远离对角线的元素越大,CON越大。 -
相关:是度量空间灰度共生矩阵元素在行或列方向上的相似程度。相关值大小反映了图像中局部灰度相关性。
当GLCM中的元素值均匀相等时,相关值就大;相反,如果GLCM中的元素值相差很大,则相关值小。当图像有水平方向的纹理时,水平方向矩阵的COR大于其余矩阵的COR值。 -
熵: 是图像所具有的信息量的度量,纹理信息也属于图像的信息,是一个随机性的度量,当共生矩阵中所有元素有最大的随机性时、空间共生矩阵中所有值几乎相等时、共生矩阵中元素分散分布时,熵较大。它表示了图像中纹理的非均匀程度或复杂程度。
-
逆差距:反映图像纹理的同质性,度量图像纹理局部变化的多少。其值大则说明图像纹理的不同区域间缺少变化,局部非常均匀。
import cv2
import math
#定义最大灰度级数
gray_level = 16
def maxGrayLevel(img):
max_gray_level=0
(height,width)=img.shape
print height,width
for y in range(height):
for x in range(width):
if img[y][x] > max_gray_level:
max_gray_level = img[y][x]
return max_gray_level+1
def getGlcm(input,d_x,d_y):
srcdata=input.copy()
ret=[[0.0 for i in range(gray_level)] for j in range(gray_level)]
(height,width) = input.shape
max_gray_level=maxGrayLevel(input)
#若灰度级数大于gray_level,则将图像的灰度级缩小至gray_level,减小灰度共生矩阵的大小
if max_gray_level > gray_level:
for j in range(height):
for i in range(width):
srcdata[j][i] = srcdata[j][i]*gray_level / max_gray_level
for j in range(height-d_y):
for i in range(width-d_x):
rows = srcdata[j][i]
cols = srcdata[j + d_y][i+d_x]
ret[rows][cols]+=1.0
for i in range(gray_level):
for j in range(gray_level):
ret[i][j]/=float(height*width)
return ret
def feature_computer(p):
Con=0.0
Eng=0.0
Asm=0.0
Idm=0.0
for i in range(gray_level):
for j in range(gray_level):
Con+=(i-j)*(i-j)*p[i][j]
Asm+=p[i][j]*p[i][j]
Idm+=p[i][j]/(1+(i-j)*(i-j))
if p[i][j]>0.0:
Eng+=p[i][j]*math.log(p[i][j])
return Asm,Con,-Eng,Idm
def test(image_name):
img = cv2.imread(image_name)
try:
img_shape=img.shape
except:
print 'imread error'
return
img=cv2.resize(img,(img_shape[1]/2,img_shape[0]/2),interpolation=cv2.INTER_CUBIC)
img_gray=cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
glcm_0=getGlcm(img_gray, 1,0)
#glcm_1=getGlcm(src_gray, 0,1)
#glcm_2=getGlcm(src_gray, 1,1)
#glcm_3=getGlcm(src_gray, -1,1)
asm,con,eng,idm=feature_computer(glcm_0)
return [asm,con,eng,idm]
if __name__=='__main__':
result = test("test.bmp")
print(result)
3 Color(颜色空间转换)
3.1 颜色空间
颜色空间,又称彩色模型(彩色空间或彩色系统),用于在某些标准下用通常可接受的方式对彩色加以说明。
常用的颜色空间有RGB、HSV、Lab等。
3.1.1 RGB
RGB颜色空间是从颜色发光的原理来进行设定的,简单来说:RGB的颜色混合方式是通过红、绿、蓝这三种光相互混合而来的。色彩相混,同时亮度等于二者亮度之总和,并且越是混合,亮度越高,即加法混合。
红、绿、蓝三个颜色通道每种色各分为256阶亮度。在0时,该颜色对应的灯是关掉的;在255时,该颜色对应的灯是最亮的。 当三色灰度数值相同时,会产生不同灰度值的灰色调,即三色灰度都为0时,是最暗的黑色调;三色灰度都为255时,是最亮的白色调。
在这里插入图片描述
分离RGB三通道图像显示
image = imread('image.jpg')
(R, G, B) = cv2.split(image)
zeros = np.zeros(image.shape[:2],dtype='uint8')
show(cv2.merge([R,zeros,zeros]))
show(cv2.merge([zeros,G,zeros]))
show(cv2.merge([zeros,zeros,B]))
3.1.2 HSV
HSV是一种比较直观的颜色模型,HSV颜色空间可以更好的数字化处理颜色。这个模型中颜色的参数分别是:色调(H, Hue),饱和度(S,Saturation),明度(V, Value)。
-
色调H:
用角度度量,取值范围为0°~360°,从红色开始按逆时针方向计算,红色为0°,绿色为120°,蓝色为240°。它们的补色是:黄色为60°,青色为180°,品红为300° -
饱和度S:
饱和度S表示颜色接近光谱色的程度。一种颜色,可以看成是某种光谱色与白色混合的结果。其中光谱色所占的比例愈大,颜色接近光谱色的程度就愈高,颜色的饱和度也就愈高。饱和度高,颜色则深而艳。光谱色的白光成分为0,饱和度达到最高。通常取值范围为0%~100%,值越大,颜色越饱和。 -
明度V:
明度表示颜色明亮的程度,对于光源色,明度值与发光体的光亮度有关;对于物体色,此值和物体的透射比或反射比有关。通常取值范围为0%(黑)到100%(白)。
image = imread('image.jpg')
hsv = cv2.cvtColor(image, cv2.COLOR_RGB2HSV)
zeros = np.zeros(image.shape[:2],dtype='uint8')
for (name,chan) in zip(('H','S','V'), cv2.split(hsv)):
cv2.imshow(name,chan)
cv2.waitKey(0)
cv2.destroyAllWindows()
3.1.3 LAB
Lab颜色空间用于计算机色调调整和彩色校正。该空间是三维直角坐标系统。是目前最受广用的测色系统。以明度L和色度坐标a*、b来表示颜色在色空间中的位置。l表示颜色的明度,a正值表示偏红,负值表示偏绿;b正值表示偏黄,负值表示偏蓝。
L:表示颜色的明度。
A:正值表示红色,负值表示绿色。
B:正值表示黄色,负值表示蓝色
image = imread('image.jpg')
lab = cv2.cvtColor(image, cv2.COLOR_RGB2LAB)
zeros = np.zeros(image.shape[:2],dtype='uint8')
for (name,chan) in zip(('L','A','B'), cv2.split(lab)):
cv2.imshow(name,chan)
cv2.waitKey(0)
cv2.destroyAllWindows()
3.1.4 GRAY(灰度变换)
image = cv2.imread('image.jpg')
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
cv2.imshow('original',image)
cv2.imshow('gray',gray)
cv2.waitKey(0)
cv2.destroyAllWindows()
4. HOG
4.1 原理
方向梯度直方图(Histogram of Oriented Gradient, HOG)特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子。它通过计算和统计图像局部区域的梯度方向直方图来构成特征。HOG+SVM可用于行人检测。
HOG的主要思想: 在一副图像中,局部目标的表象和形状(appearance and shape)能够被梯度或边缘的方向密度分布很好地描述。(本质:梯度的统计信息,而梯度主要存在于边缘的地方)
具体的实现方法是:首先将图像分成小的连通区域,我们把它叫细胞单元。然后采集细胞单元中各像素点的梯度的或边缘的方向直方图。最后把这些直方图组合起来就可以构成特征描述器。
HOG特征提取算法的实现过程:
- 将一个image灰度化(将图像看做一个x,y,z(灰度)的三维图像
- 采用Gamma校正法对输入图像进行颜色空间的标准化(归一化);目的是调节图像的对比度,降低图像局部的阴影和光照变化所造成的影响,同时可以抑制噪音的干扰;
- 计算图像每个像素的梯度(包括大小和方向);主要是为了捕获轮廓信息,同时进一步弱化光照的干扰。
- 将图像划分成小cells(例如6*6像素/cell);
- 统计每个cell的梯度直方图(不同梯度的个数),即可形成每个cell的descriptor;
- 将每几个cell组成一个block(例如3*3个cell/block),一个block内所有cell的特征descriptor串联起来便得到该block的HOG特征descriptor。
- 将图像image内的所有block的HOG特征descriptor串联起来就可以得到该image(你要检测的目标)的HOG特征descriptor了。这个就是最终的可供分类使用的特征向量了。

import cv2
import numpy as np
import math
import matplotlib.pyplot as plt
class Hog_descriptor():
def __init__(self, img, cell_size=16, bin_size=8):
self.img = img
self.img = np.sqrt(img / np.max(img))
self.img = img * 255
self.cell_size = cell_size
self.bin_size = bin_size
self.angle_unit = 360 // self.bin_size
assert type(self.bin_size) == int, "bin_size should be integer,"
assert type(self.cell_size) == int, "cell_size should be integer,"
assert type(self.angle_unit) == int, "bin_size should be divisible by 360"
def extract(self):
height, width = self.img.shape
gradient_magnitude, gradient_angle = self.global_gradient()
gradient_magnitude = abs(gradient_magnitude)
cell_gradient_vector = np.zeros((height // self.cell_size, width // self.cell_size, self.bin_size))
for i in range(cell_gradient_vector.shape[0]):
for j in range(cell_gradient_vector.shape[1]):
cell_magnitude = gradient_magnitude[i * self.cell_size:(i + 1) * self.cell_size,
j * self.cell_size:(j + 1) * self.cell_size]
cell_angle = gradient_angle[i * self.cell_size:(i + 1) * self.cell_size,
j * self.cell_size:(j + 1) * self.cell_size]
cell_gradient_vector[i][j] = self.cell_gradient(cell_magnitude, cell_angle)
hog_image = self.render_gradient(np.zeros([height, width]), cell_gradient_vector)
hog_vector = []
for i in range(cell_gradient_vector.shape[0] - 1):
for j in range(cell_gradient_vector.shape[1] - 1):
block_vector = []
block_vector.extend(cell_gradient_vector[i][j])
block_vector.extend(cell_gradient_vector[i][j + 1])
block_vector.extend(cell_gradient_vector[i + 1][j])
block_vector.extend(cell_gradient_vector[i + 1][j + 1])
mag = lambda vector: math.sqrt(sum(i ** 2 for i in vector))
magnitude = mag(block_vector)
if magnitude != 0:
normalize = lambda block_vector, magnitude: [element / magnitude for element in block_vector]
block_vector = normalize(block_vector, magnitude)
hog_vector.append(block_vector)
return hog_vector, hog_image
def global_gradient(self):
gradient_values_x = cv2.Sobel(self.img, cv2.CV_64F, 1, 0, ksize=5)
gradient_values_y = cv2.Sobel(self.img, cv2.CV_64F, 0, 1, ksize=5)
gradient_magnitude = cv2.addWeighted(gradient_values_x, 0.5, gradient_values_y, 0.5, 0)
gradient_angle = cv2.phase(gradient_values_x, gradient_values_y, angleInDegrees=True)
return gradient_magnitude, gradient_angle
def cell_gradient(self, cell_magnitude, cell_angle):
orientation_centers = [0] * self.bin_size
for i in range(cell_magnitude.shape[0]):
for j in range(cell_magnitude.shape[1]):
gradient_strength = cell_magnitude[i][j]
gradient_angle = cell_angle[i][j]
min_angle, max_angle, mod = self.get_closest_bins(gradient_angle)
orientation_centers[min_angle] += (gradient_strength * (1 - (mod / self.angle_unit)))
orientation_centers[max_angle] += (gradient_strength * (mod / self.angle_unit))
return orientation_centers
def get_closest_bins(self, gradient_angle):
idx = int(gradient_angle / self.angle_unit)
mod = gradient_angle % self.angle_unit
return idx, (idx + 1) % self.bin_size, mod
def render_gradient(self, image, cell_gradient):
cell_width = self.cell_size / 2
max_mag = np.array(cell_gradient).max()
for x in range(cell_gradient.shape[0]):
for y in range(cell_gradient.shape[1]):
cell_grad = cell_gradient[x][y]
cell_grad /= max_mag
angle = 0
angle_gap = self.angle_unit
for magnitude in cell_grad:
angle_radian = math.radians(angle)
x1 = int(x * self.cell_size + magnitude * cell_width * math.cos(angle_radian))
y1 = int(y * self.cell_size + magnitude * cell_width * math.sin(angle_radian))
x2 = int(x * self.cell_size - magnitude * cell_width * math.cos(angle_radian))
y2 = int(y * self.cell_size - magnitude * cell_width * math.sin(angle_radian))
cv2.line(image, (y1, x1), (y2, x2), int(255 * math.sqrt(magnitude)))
angle += angle_gap
return image
img = cv2.imread('lena.jpg', cv2.IMREAD_GRAYSCALE)
hog = Hog_descriptor(img, cell_size=4, bin_size=4)
vector, image = hog.extract()
print(np.array(vector).shape)
plt.imshow(image, cmap=plt.cm.gray)
plt.show()
参考资料链接
Image Histogram
图像特征:GLCM
opencv颜色空间转换
HOG特征
















