模型压缩——量化

量化

int
int8取值范围是-128 - 127（符号位+数值位=8)
Int16 意思是16位整数(16bit integer)，相当于short 占2个字节 -32768 ~ 32767
Int32 意思是32位整数(32bit integer), 相当于 int 占4个字节 -2147483648 ~ 2147483647
Int64 意思是64位整数(64bit interger), 相当于 long long 占8个字节 -9223372036854775808 ~ 9223372036854775807
float
一个float单精度浮点数一般是4bytes（32bit）来表示，由三部分组成：符号位、指数部分（表示2的多少次方）和尾数部分（小数点前面是0，尾数部分只表示小数点后的数字）
双精度64位，单精度32位，半精度自然是16位
float32: 单精度浮点数float的这三部分所占的位宽分别为：1，8，23
float16: 半精度浮点数half的这三部分所占的位宽分别为：1，5，10
量化的作用：更小的模型尺寸、更低的功耗、更快的计算速度。下图是不同数据结构比较及执行基本运算时的计算消耗。
float32转为int时都是转为int8的原因是：float32的指数部分位宽为8，截断小数部分后就等于int8；虽然int16占用的字节比float32少，但使用int8就能够表示float32的整数部分，所以float32不转为int16。
定点：指的是小数点的位置是固定的，即小数位数是固定的数。
在量化的实现代码中要做溢出保护，加个clip

对称量化和非对称量化

浮点转到定点：$Q=round(\frac{R}{S})+Z$
定点转到浮点：$R=(Q-Z)\ast S$
$R$代表真实浮点值，$Q$代表量化后的定点值，$Z$(Zero)表示0浮点值对应的量化定点值，$S$(Scale)表示定点量化后可表示的最小刻度。
$S=\frac{R_{max}-R_{min}}{Q_{max}-Q_{min}}$
$R_{max}/R_{min}$代表最大/最小的浮点值，$Q_{max}/Q_{min}$代表最大/最小的定点值。
$Z=Q_{max}-\frac{R_{max}}{S}$
比如进行int8的量化，数据范围是[-128,127]，浮点的最大值最小值分别是$X_{max}$和$X_{min}$，$X_q$表示量化后的数据，$X_f$表示浮点数据。
$X_q=\frac{X_f}{S}+Z$
$S=\frac{X_{max}-X_{min}}{127-(-128)}$
$Z=0-round(\frac{X_{min}}{S})$ or $Z=255-round(\frac{X_{max}}{S})$
round代表四舍五入
量化分为对称量化和非对称量化，上面的是非对称量化，如果是对称量化，则是将原浮点数的范围由$[X_{min},X_{max}]$扩充为$[-X_{max},X_{max}]$，这里假定 $|Xmax|>|Xmin|$。
对称量化图示：

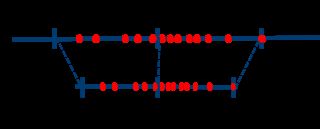
非对称量化图示：

$S$除了上述的公式为还可以采用以下公式：
对称量化：$S=\frac{2^{n-1}-1}{max(|x|)}$
非对称量化：$S=\frac{2^{n-1}-1}{max(x)-min(x)}$
$x$代表浮点数,$n$代表量化后的位宽，float32量化为int8则n为8。

矩阵量化

假设$R_1$和$R_2$是浮点实数上的两个$N\times N$的矩阵，$R_3$是$R_1$和$R_2$相乘后的矩阵：
$R_3^{i,k}={\sum }_{j=1}^N{R}_1^{i,j}{R}_2^{j,k}$
假设$S_1$和$Z_1$ 是$R_1$矩阵对应的 scale 和 zero point，$S_2$、$Z_2$、 $S_3$、$Z_3$ 同理，那么通过上式可以推出：
$S_3(Q_3^{i,k}-Z_3)={\sum }_{j=1}^N{S}_1(Q_1^{i,j}-Z_2)S_2(Q_2^{j,k}-Z_2)$
=>$Q_3^{i,k}=\frac{S_1{S}_2}{S_3}{\sum }_{j=1}^N(Q_1^{i,j}-Z_2)(Q_2^{j,k}-Z_2)+Z_3$
除了$\frac{S_1{S}_2}{S_3}$外都是定点运算，此时设$M=\frac{S_1{S}_2}{S_3}$,$M$在$(0,1)$之间(这是通过大量实验统计出来的)，因此可以表示成$M=2^{-n}{M}_0$，其中$M_0$是一个定点实数。因此，如果存在$M=2^{-n}{M}_0$，那我们就可以通过$M_0$的 bit 位移操作实现$2^{-n}{M}_0$，这样整个过程就都在定点上计算了(其实这是由误差的，用这种方法可以得到一个近似的结果)。

卷积网络的量化

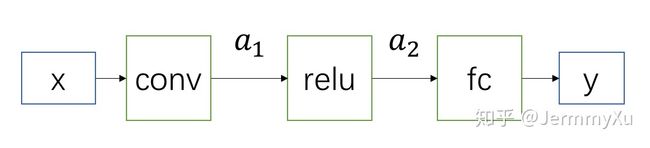
卷积和全连接的本质就是矩阵运算。
假设网络为上图，则这个网络只有三个模块，现在需要把 conv、fc、relu 量化。
假设输入为$x$，我们可以事先统计样本的最大值和最小值，然后计算出$S_x$(scale) 和$Z_x$ (zero point)。
同样地，假设 conv、fc 的参数为$w_1$、$w_2$，以及 scale 和 zero point 为$S_{w_1}$、$Z_{w_1}$ 、$S_{w_2}$ 、$Z_{w_2}$ 。中间层的 feature map 为$a_1$、$a_2$，并且事先统计出它们的 scale 和 zero point 为$S_{a_1}$、$Z_{a_1}$ 、$S_{a_2}$ 、$Z_{a_2}$ 。
（不考虑bias）
$a_1^{i,k}={\sum }_{j=1}^N{x}^{i,j}{w}_1^{j,k}$=>$Q_{a_1}^{i,k}=M{\sum }_{j=1}^N(Q_x^{i,j}-Z_x)(Q_{w_1}^{j,k}-Z_{w_1})+Z_{a_1}$($M=\frac{S_{w_1}{S}_x}{S_{a_1}}$)
得到 conv 的输出后，我们不用反量化回$a_1$，直接用$Q_{a_1}$继续后面的计算即可。
量化后的ReLU的计算公式为$Q_{a_2}=max(Q_{a_1},Z_{a_1})$
量化后的fc层计算公式为：
$Q_y^{i,k}=M{\sum }_{j=1}^N(Q_{a_2}^{i,j}-Z_{a_2})(Q_{w_2}^{j,k}-Z_{w_2})+Z_y$
然后通过公式$y=S_y(Q_y-Z_y)$把结果反量化回去，就可以得到近似原来全精度模型的输出了。
可以看到，上面整个流程都是用定点运算实现的。我们在得到全精度的模型后，可以事先统计出 weight 以及中间各个 feature map 的 min、max，并以此计算出 scale 和 zero point，然后把 weight 量化成 int8/int16 型的整数后，整个网络便完成了量化，然后就可以依据上面的流程做量化推理了。
Conv输出的Scale和zero point需要用一些样本去跑一遍，然后统计

后训练量化(post training quantization)

后训练量化指的是，对预训练后的网络选择合适的量化操作和校准操作，以实现量化损失的最小化，该过程不需要训练，通常不直接更新权重原始数值而是选用合适的量化参数
卷积层的量化(带bias)：
conv: $a={\sum }_i^N{w}_i{x}_i+b$
量化后的Conv: $S_a(Q_a-Z_a)={\sum }_i^N{S}_w(Q_w-Z_w)S_x(Q_x-Z_x)+S_b(Q_b-Z_b)$
=>$Q_a=\frac{S_w{S}_x}{S_a}{\sum }_i^N(Q_w-Z_w)(Q_x-Z_x)+\frac{S_b}{S_a}(Q_b-Z_b)+Z_a$
此时采用$S_w{S}_x$来代替$S_b$来量化bias(R和Q是通过S和Z来实现映射关系，只要能实现相互映射，那么S和Z怎么取值都可以，只是不同的取值方法需要付出不同的代价)，并令$Z_b=0$(对称量化)，那么:
$Q_a=\frac{S_w{S}_x}{S_a}({\sum }_i^N(Q_w-Z_w)(Q_x-Z_x)+Q_b)+Z_a=M({\sum }_i^N{Q}_w{Q}_x-{\sum }_i^N{Q}_w{Z}_x-{\sum }_i^N{Q}_x{Z}_w+{\sum }_i^N{Z}_x{Z}_w+Q_b)+Z_a$，$M=\frac{S_w{S}_x}{S_a}$
采用$S_w{S}_b$来代替$S_b$的代价：
$S_w$和$S_x$分别是将浮点值缩放到int8($\frac{2}{2^8}$)，$S_w{S}_x$是将浮点值缩放到int16($\frac{4}{2^{16}}$)，而$S_b$通常将浮点值缩放到int32($\frac{2}{2^{32}}$)，此时用$S_w{S}_b$来代替$S_b$就变成将浮点值缩放到int16，会导致精度损失。不过，大部分情况下这点损失是可以忽略的，对效果影响不大，而代码实现上却可以更加高效，因此，这就成了一个约定俗成的操作了。

量化感知训练

Straight Through Estimator
round会导致weight的梯度都为0，这就无法训练了。
那要怎么解决这个问题呢？

一个很容易想到的方法是，直接跳过伪量化的过程，避开 round。直接把卷积层的梯度回传到伪量化之前的 weight 上。这样一来，由于卷积中用的 weight 是经过伪量化操作的，因此可以模拟量化误差，把这些误差的梯度回传到原来的 weight，又可以更新权重，使其适应量化产生的误差，量化训练就可以正常进行下去了。

这个方法就叫做 Straight Through Estimator(STE)。
Pytorch里的code实现示例：https://zhuanlan.zhihu.com/p/158776813

Fold BN 和ReLU

BN

BN和Conv融合的过程看：https://blog.csdn.net/weixin_39994739/article/details/123872722 中的RepVGG
融合后的新Conv表达式：$y_{bn}={\sum }_i^N{\gamma }^{\prime }{w}_i{x}_i+{\gamma }^{\prime }(b-{\mu }_y+\beta )$，${\gamma }^{\prime }=\frac{\gamma }{\sqrt{{\sigma }_y^2+ϵ}}$
$\gamma$和$\beta$分别为BN的缩放因子和平移尺度，$w_i$为原来Conv的weight，$x_i$为原来Conv的输入。
此时新Conv的weight和bias分别为$w_i^{\prime }={\gamma }^{\prime }{w}_i$和$b^{\prime }={\gamma }^{\prime }(b-{\mu }_y)+\beta$
量化网络时可以将BN融合到Conv中，如果量化时不想更新 BN 的参数 (比如后训练量化)，那我们就先把 BN 合并到 Conv 中，直接量化新的 Conv 即可。
如果量化时需要更新 BN 的参数 (比如量化感知训练)，需要在forward里更新BN的均值($\mu$)和方差($\sigma$），更新算法为momentum。如图：在生成融合后的Conv的weight前会先按原来的流程先走原来的Conv+BN，然后使用momentum算法更新BN的($\mu$)和($\sigma$），然后将更新后的BN与原来的Conv融合成一个新的Conv，再重新走这个融合后的Conv。（融合后的Conv需要BN的$\sigma$，所以量化训练时要更新BN的参数就要；并且融合后的Conv由BN和原来的Conv组成，它是用来估计量化误差来回传梯度，它的weight在训练的时候不会更新，模型只会更新原来的Conv和BN里的参数，然后再用更新后的原来Conv和BN组成新的融合的Conv）

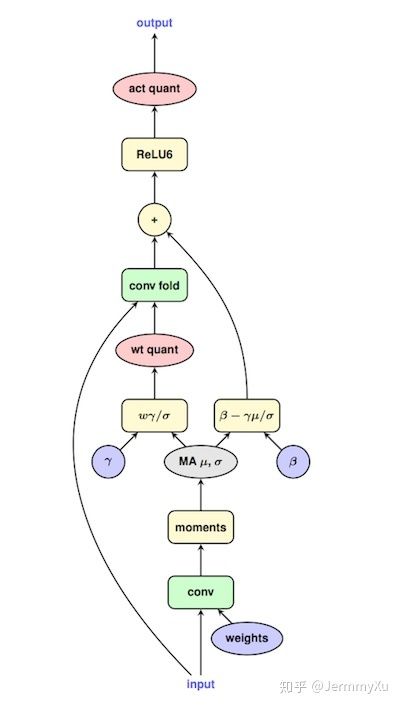
所谓的更新BN参数是值在forward的时候更新不更新($\mu$)和($\sigma$），融合时用的$\gamma$和$\beta$为训练好的全精度模型里的BN层的值（训练全精度模型不融合BN，量化时才融合），量化时只更新BN的$\mu$和$\sigma$。

ReLU

在全精度里Conv和ReLU是无法融合的，ReLU是一个截断函数，无法将定点反量化成float。

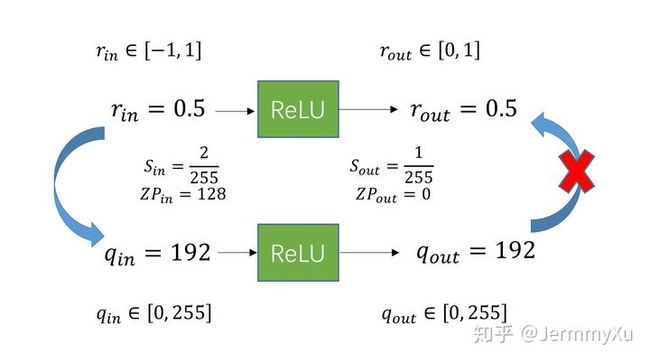
如果使用 ReLU 之后的 scale 和 zp，那我们就可以用量化本身的截断功能来实现 ReLU的作用。
在量化里：$Q=round(\frac{R}{S}+Z)$
$round$除了把 float 型四舍五入转成 int 型外，还需要保证$Q$ 的数值在特定范围内「例如 0～255」，相当于要做一遍 clip (截断)操作。因此，这个公式更准确的写法应该是「假设量化到 uint8 数值」：
$Q=round(clip(\frac{R}{S}+Z,0,255))$
此时就可以用量化的clip来模拟ReLU，量化融合后的Conv的公式就如上

这里可能有人会觉得ReLU并没有和Conv融合，其实这里是将：量化Conv输出(ReLU的输入)+量化ReLU，融合成量化Conv的输出，从而省去了ReLU这个操作。
在上面的卷积量化里说到可以直接使用$Q_{a_1}$，不用再反量化回去，而在求$Q_{a_1}$时使用了$S_{a_1}$和$Z_{a_1}$，此时就用这两个参数用$Q_{out}$和$Z_{out}$和clip代替。

ReLU量化：数学角度和物理含义

$ReLU(x)=\{\begin{array}{l}x，x\ge 0\\ 0，x<0\end{array}$
=>$r_2=\{\begin{array}{l}{r}_1，r_1\ge 0\\ 0，r_1<0\end{array}$
=>$S_2(q_2-Z_2)=\{\begin{array}{l}{S}_1(q_1-Z_1)，q_1\ge Z_1\\ 0，q_1<Z_1\end{array}$
=>$q_2=\{\begin{array}{l}\frac{S_1}{S_2}(q_1-Z_1)+Z_2，q_1\ge Z_1\\ Z_2，q_1<Z_1\end{array}$
ReLU的结果的范围为大于等于$(0,+\infty )$，而量化后数值范围为$(0,255)$，为保证0点的对齐，$Z_2$只能取0。
具体实现上没有必要完全按照公式来操作。一：公式内的 scale 操作过于麻烦还掉精度，二： ReLU 本身是有明确的物理意义的，那就是把小于零点的数值截断，其余不变。这个意义在量化里面依然成立。
因此，更简洁明了的方式来实现量化的 ReLU：$q_2=\{\begin{array}{l}{q}_1，q_1\ge Z_1\\ Z_1，q_1<Z_1\end{array}$
此时，ReLU 前后的 scale 和 zeropoint保持一致

ReLU与Conv的fold

Conv的量化公式：$S_3(q_3-Z_3)=S_1{S}_2{\sum }_i^N(q_1-Z_1)(q_2-Z_2)$
Conv后进ReLU：$S_4(q_4-Z_4)=\{\begin{array}{l}{S}_3(q_3-Z_3),q_3\ge Z_3,\\ 0,q_3<Z_3\end{array}=\{\begin{array}{l}{S}_1{S}_2{\sum }_i^N(q_1-Z_1)(q_2-Z_2),q_3\ge Z_3,\\ 0,q_3<Z_3\end{array}$
=>$q_4=\{\begin{array}{l}\frac{S_1{S}_2}{S_4}{\sum }_i^N(q_1-Z_1)(q_2-Z_2)+Z_4,q_3\ge Z_3,\\ Z_4,q_3<Z_3\end{array}$
当量化到int8时需要对数值进行(0,255)的clip，
那么公式应该为：$q_4=\{\begin{array}{l}clip(\frac{S_1{S}_2}{S_4}{\sum }_i^N(q_1-Z_1)(q_2-Z_2)+Z_4,0,255),q_3\ge Z_3,\\ Z_4,q_3<Z_3\end{array}$
在上面说了$Z_4=0$，那么当$q_3<Z_3$等价于${\sum }_i^N(q_1-Z_1)(q_2-Z_2)<0$(因为Scale都是大于0的数)，所以$q_4=clip(\frac{S_1{S}_2}{S_4}{\sum }_i^N(q_1-Z_1)(q_2-Z_2)+Z_4,0,255)=0=Z_4$。最后都可以统一用下面这个式子来表示：$q_4=clip(\frac{S_1{S}_2}{S_4}{\sum }_i^N(q_1-Z_1)(q_2-Z_2),0,255)$
这个公式的意义相当于：计算出 ReLU 之后的$S$和$Z$，然后把这个$S$和$Z$对应到 Conv 的输出，这样一来，ReLU 的运算就合并到 Conv 里面了。
正如前面提到的，ReLU 除了做数值上的截断外，其实没有其他操作了，而量化本身自带截断操作，因此才能把 ReLU 合并到 Conv 或者 FC 等操作里面。

Add和Concat

如果允许的话可以先将Add/Concat和Conv融合，然后再量化这个融合后的Conv，不允许再来逐个量化。
融合方法：https://blog.csdn.net/weixin_39994739/article/details/123872722

Add

全精度下Add可以表示为：$r_3=r_1+r_2$
将量化的公式带入后：$S_3(q_3-Z_3)=S_1(q_1-Z_1)+S_2(q_2-Z_2)$=>$q_3=\frac{S_1}{S_3}(q_1-Z_1)+\frac{S_2}{S_3}(q_2-Z2)+Z_3$
此时，$\frac{S_1}{S_3}$和$\frac{S_2}{S_3}$需要转为定点，转换方法看矩阵量化

Concat

$r_3=concat[r_1,r_2]$
代入量化公式：$S_3(q_3-Z_3)=concat[S_2(q_2-Z_2),S_2(q_2-Z_2)]$
=>$q_3=concat[\frac{S1}{S3}(q_1-Z_1)+Z_3,\frac{S2}{S3}(q_2-Z_2)+Z_3]$
在这里是将$r_1$和$r_2$的取值范围的合集作为$r_3$的取值范围，此时计算$r_3$的scale和zero point使用的minmax就可以求出来，最后$r_3$对应的定点就可以通过上式求得。

激活函数

激活函数分线性和非线性，其中LeakyReLU的量化如下，而上图中其它激活函数的量化同理。

LeakyReLU

$LeakyReLU(x)=\{\begin{array}{l}x，x\ge 0\\ \alpha x，x<0\end{array}$
$\alpha$一般为0~1之间的小数。
float公式：$r_2=\{\begin{array}{l}{r}_1，r_1\ge 0\\ \alpha r_1，r_1<0\end{array}$
量化公式：$S_2(q_2-Z_2)=\{\begin{array}{l}{S}_1(q_1-Z_1)，q_1\ge Z_1\\ \alpha S_1(q_1-Z_1)，q_1<Z_1\end{array}$
=>$q_2=\{\begin{array}{l}\frac{S_1}{S_2}(q_1-Z_1)+Z_2，q_1\ge Z_1\\ \frac{\alpha S_1}{S_2}(q_1-Z_1)+Z_2，q_1<Z_1\end{array}$

非线性激活函数

gemmlowp只给出了sigmoid和tanh的32bit定点估计实现，但是可以推广到ELU、SELU、swish、mish等激活函数，源代码链接https://link.zhihu.com/?target=https%3A//github.com/google/gemmlowp/blob/master/fixedpoint/fixedpoint.h

1. 激活函数的变形

sigmoid以$y=0.5$进行进行中心对称，tanh以$y=0$进行中心对称。

经过变形后，可以看出来计算的关键是对 $\frac{1}{(1+e^{-x})/2}$和$\frac{1}{(1+e^{-2x})/2}$进行定点估计。以$\frac{1}{(1+e^{-x})/2}$为例，计算其定点估计分两步：
1.计算分母$D=1+e^{-x}$的定点估计；
2.计算除法$\frac{1}{D/2}$的定点估计。

2. 误差估计：1+exp(-x)的32bit定点精度

当$x>0$时，$0<e^{-x}<1$。这条性质是保证定点估计在32bit时几乎无精度损失的关键。
假设将整数 1 表示成为 32bit 的定点，其二进制表示为$\underset{31个0}{1000\cdots 000}$，
那么$1+e^{-x}$的最大值不会超过$\underset{31个0}{1111\cdots 111}$，
并且 32bit 的定点表示的误差不超过$1/2^{31}=4.657\times 10^{-10}$

3. 计算1+exp(-x)的32bit定点估计：$x\ge 0.25$时，查表法LUT

对于 x ≥ 0.25 的时，为了保证计算速度，计算结果直接用查表进行，而不是泰勒展开。查表值如下：

浮点值	定点表示对应的无符号 int32 值	绝对误差（真实浮点值 - int32 值 / 2^31 ）
exp(-0.25)	1672461947	1.418e-10
exp(-0.5)	1302514674	1.94e-10
exp(-1)	790015084	1.634e-10
exp(-2)	290630308	1.173e-10
exp(-4)	39332535	0.076e-10
exp(-8)	720401	2.291e-10
exp(-16)	242	1.549e-10

有了这个表格，对于其他 x ≥ 0.25 的值，以 exp(-5) 的 32bit 定点估计为例，可以如下计算：
$e^{-5}\approx LUT(e^{-4})\ast LUT(e^{-1})\approx (39332535x790015084)>>32=7234815$
其中 >> 32 是指 两个 32bit 整数相乘后再右移32位。因为两个 32bit 整数相乘结果不会超过 64bit，只取其中最高的 32bit 作为定点近似结果。
那么这样做的理论误差为：
$e^{-5} = ( LUT(e^{-4}) + δ(e^{-4})) * ( LUT(e^{-1}) + δ(e^{-1}))
$
$\approx LUT(e^{-4})\ast LUT(e^{-1})+LUT(e^{-4})\ast \delta (e^{-1})+\delta (e^{-4})\ast LUT(e^{-1})<LUT(e^{-4})\ast LUT(e^{-1})+\delta (e^{-1})+\delta (e^{-4})$
查表法能估计的最大 x 为 31.75，即
$e^{-31.75}=e^{-0.25}\ast e^{-0.5}\ast e^{-1}\ast e^{-2}\ast e^{-4}\ast e^{-8}\ast e^{-16}$
误差不超过:$\delta (e^{-0.25})\ast \delta (e^{-0.5})\ast \delta (e^{-1})\ast \delta (e^{-2})\ast \delta (e^{-4})\ast \delta (e^{-8})\ast \delta (e^{-16})$
问题1：要是$x\ge 32$怎么办？
$e^{-32}$直接近似为0，$1 + e^{-32}近似等于 1，误差不会超过 4.657e-10。
问题2：x = 0.1 怎么计算，或者 x = 5.1 怎么计算？
$e^{-5.1}=-e^{-4}\ast e^{-1}\ast e^{-0.1}$
对于剩下的 $e^{-0.1}$，由于 x 接近 0， $e^{-x}$接近1，因此查表法精度不够，需要用到泰勒展开。

4. 计算 $1+e^{-x}$ 的 32bit 定点估计：x < 0.25时，泰勒展开

gemmlowp中，对 $e^{-x}$在 x < 0.25 时的近似，为在 x=0.125 处进行4阶泰勒展开近似（还可以选择3阶甚至2阶，或者可以在x=0.25处展开）：
$e^{-x}\approx e^{-0.125}(1+(0.125-x)+\frac{1}{2}(0.125-x{)}^2+\frac{1}{2\cdot 3}(0.125-x{)}^3+\frac{1}{2\cdot 2\cdot 2\cdot 3}(0.125-x{)}^4)$
那么需要额外增加3个查表值：

浮点值	定点表示对应的无符号 int32 值	绝对误差（真实浮点值 - int32 值 / 2^31 ）
$e^{-0.125}$	715827883	1.552e-10
0.125	536870912	0
1 / 3	1895147668	1.345e-10

除此之外，泰勒展开中 1 / 2 的系数可以用定点右移来计算。
那么到这里，1 + exp(-x) 的 定点近似估计就完成了。

5. 计算 1 / D 的 定点估计

定点的除法，通常是用牛顿法(newton-raphson)转换为若干个定点乘法来计算的。
如果要求解 1 / D 的值，就是计算函数$f(X)=1/X-D=0$的解。那么按照牛顿法的迭代公式为:
$X_{i+1}=X_i-\frac{f(X_i)}{f^{\prime }(X_i)}=X_i-\frac{1/X_i-D}{-1/X_i^2}=X_i+X_i(1-D{X}_i)$
每次迭代，1 / D 的估计误差是按平方下降，即
$1-D{X}_{i+1}=1-D(X_i+X_i(1-D{X}_i))=(1-D{X}_i{)}^2$
所以从定点的角度，每次迭代后误差位就会翻倍（假设，初始 $X_0$的误差是在从左起第1个bit，那么$X_1$的误差是在从左起第2个bit，$X_2$的误差是在从左起第4个bit，$X_3$的误差是在从左起第8个bit，以此类推，知道误差超过了定点表示的范围就可以忽略不计）。
newton-raphson算法指出，当 $D\in [0.5,1]$时，取$X_0=48/17-32/17\ast D$，那么
$X_1$的精度满足8bit定点表示，
$X_2$的精度满足16bit定点表示，
$X_3$的精度满足32bit定点表示，所以最多迭代3次即可。
当$D=1+e^{-x}$时，$D\in [1,2]$，因此不能直接计算$\frac{1}{1+e^{-x}}$，而要计算$\frac{1}{(1+e^{-x})/2}$的值。(把D乘以k，变成在[0.5,1]内，然后计算进行迭代，最后的时候再反乘以$\frac{1}{k}$)
因此，计算$\frac{1}{(1+e^{-x})/2}$的伪代码为

D = (1 + LUT(exp(-x)) / 2
X = LUT(48/17) - LUT(32/17) * D

loop i = 1 : 3
     X = X + X * (1 - D * X)
end loop

需要增加两个查表值

浮点值	定点表示对应的无符号 int32 值	绝对误差（真实浮点值 - int32 值 / 2^31 ）
48 / 17	1515870810	6.574e-10
32 / 17	1895147668	4.383e-10

总结

以上就是非线性激活函数的定点量化过程，主要包含3个步骤：

• 计算 $1+e^{-x}$ 在 x ≥ 0.25 时的定点估计
• 计算$1+e^{-x}$在 x < 0.25 时的定点估计
• 计算 1 / D 的定点估计

Per-channel量化

在考虑kernel的情况下，那么卷积运算更准确的表示应该为：
$r_3^{i,j,oc}={\sum }_{ic}{\sum }_m{\sum }_n{r}_1^{i-m,j-n,ic}{r}_2^{i-m,j-n,ic}$
$oc$代表输出通道的index，$ic$代表输入通道的index。下面为了公式简洁会省略$i$、$j$这些跟位置相关的 index。
per-layer 量化下，整个 tensor 会共用一个 scale 和 zero point。
就像下面这张图给出的这样：

因此量化后的卷积运算为：
$S_3(q_3^{oc}-Z_3)={\sum }_{ic}{\sum }_m{\sum }_n{S}_1(q_1^{ic}-Z_1)S_2(q_2^{ic}-Z_2)$
=>$q_3^{oc}=\frac{S_1{S}_2}{S_3}{\sum }_{ic}{\sum }_m{\sum }_n(q_1^{ic}-Z_1)(q_2^{ic}-Z_2)+Z_3$
per-channel 量化并非时每个channel都单独计算一个scale和zeropoint，如下图所示：

这样做的话每个channle都要算一个scale和zeropoint，虽然精度会比较高，但卷积就没法加速了，计算开销会成倍上升。
所以，实践中的per-channel 量化其实是按照下图的方式做的：

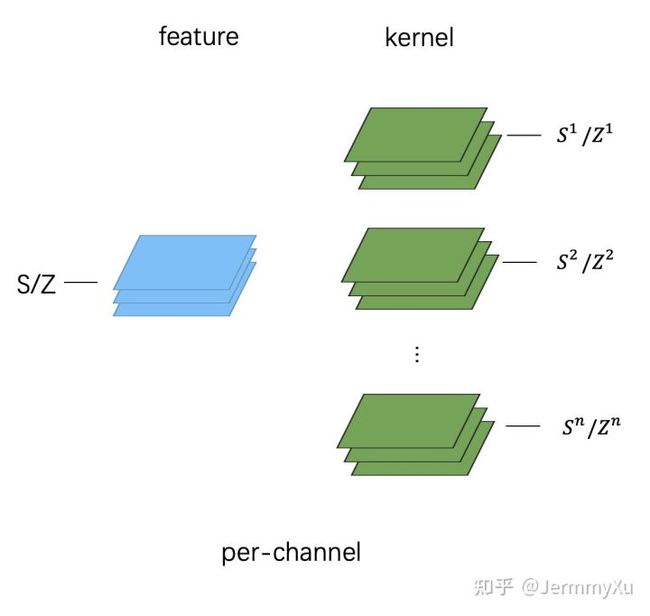
这其中的差别就在于，feature 还是整个 tensor 共用一个 scale 和 zeropoint，但每个 kernel 会单独统计一个 scale 和 zeropoint（注意是每个 kernel，而不是 kernel 的每个 channel）。
在这种定义下，per-channel 量化和 per-layer 就变得很相似了：
$S_3(q_3^{oc}-Z_3)={\sum }_{ic}{\sum }_m{\sum }_n{S}_1(q_1^{ic}-Z_1)S_2(q_2^{ic}-Z_2)$
=>$q_3^{oc}=\frac{S_1{S}_2}{S_3}{\sum }_{ic}{\sum }_m{\sum }_n(q_1^{ic}-Z_1)(q_2^{ic}-Z_2)+Z_3$
在这里的公式和上面的per-layer量化的差别是：对于不同的$oc$，$q_3^{oc}$对应的$S_2$是不一样的，因为每个 kernel 都会有自己专属的$S_2$。因此，对于每一个$oc$，需要单独用 $\frac{S_1{S}_2}{S_3}$重新 requant 一下。而在 per-layer 量化里面，我们是可以把整个 output feature 都算完，再统一 requant 的。
注意：MobileNet使用per-layer量化后很差的原因是它使用了Depthwise Separable Convolution。Depthwise Separable Convolution中由于每一张feature都是由单独的一个kernel生成的，而Depthwise Separable Convolution中每个kernel的数值分布差异很大(普通Conv里的每个kernel都对所有feature进行卷积，所以kernel之间的关联性会比较大，分布差异就不会很大)，因此导致了MobileNet使用per-layer量化后很差，而使用per-channel的结果就还行。

极端性R的矫正方法

举个栗子，如果某个 weight 里面的数值是 [-0.1, 0.2, 0.3, 255.1]，那我们统计出来的 minmax 就是 -0.1 和 255.1，如此一来，0.2、0.3 这样的数值就会被映射到同一个定点数，信息损失相当严重，而它们对结果影响可能远大于 255.1。因此，在这种情况下，我们宁愿把 255.1 损失掉，也希望尽可能把 0.2、0.3 保持下来。因此，就需要对这种极端的R进行矫正，矫正方法由底下几种。

1. 直方图截断

既然离群点影响很大，那最容易想到的解法就是排除这些离群点的干扰。我们可以把 weight 或者 feature map 的数值范围统计出一个直方图，根据直方图舍弃前后 m% 的数值，直接用剩下的数值来确定 minmax。

2. 滑动平均

除此之外，还有一种对 feature map 比较有效的统计方法。 这也是 Google 论文提到的一种技巧。我们把矫正数据集分为几个 batch，逐次输入到网络中统计数值。每次更新数值范围时，按照$r_{max}^t=r_{max}^t\ast (1-\alpha )+r_{max}^{t-1}\ast \alpha$来更新，其中，$r_{max}^{t-1}$是上一次统计到的最大值。通过控制 $\alpha$的数值，可以控制新数据对历史统计数据的影响，让最终统计到的数值能大致涵盖大部分数值，但又不会被一些离群点主导。

3. 均值和方差

一个不成文的约定：我们通常会假设 weight 和 feature 的数值呈正态分布。在此假设下，我们可以统计出测试数据中 weight 或者 feature 的均值$\mu$和方差$\sigma$，然后，根据正态分布的性质，在区间$(\mu -3\sigma ,\mu +3\sigma )$之间的数值占了 99+%，因此，可以令$r_{min}=\mu -3\sigma$、$r_{max}=\mu +3\sigma$，这样就基本涵盖了大部分数值，也避免了一些离群点的影响。

当然，如果实际的数值分布不是正态的，比如，是个双峰分布，那可能就 gg 了。

4. 数学

使用一些metric来度量当前取的minmax值是否合适。

搜索minmax

常采用的是TRT量化方法，TRT采用的是8bit对称量化，即正数区间量化到 [0, 127]，负数区间量化到 [-128, 0)。量化的大致过程如下：

1. 首先根据矫正数据集确定数值范围$[r_{min},r_{max}]$；
2. 把这个范围区间划分为 2048 份 (相当于离散化成 2048 个 bin 的直方图，具体多少 bin 可以调整)；
3. 以最前面的 128 个 bin 作为基准，逐次向后搜索，每次扩增一个 bin 的长度，得到一个新的数值范围。然后把这个数值范围重新划分为一个 128 个 bin 的直方图$Q$(这一步相当于舍弃了部分数值信息，并做了量化)；
4. 那要如何评价当前这个数值范围是否合适呢？这个时候 KL 散度就能派上用场了。我们把剩下那些没有搜索到的数值压缩到当前搜索到的 bin 上，得到一个信息基本没有损失的直方图$P$，如果我们之前搜索到的$Q$跟$P$相比信息损失最小 (即 KL 散度最小)，那这个$Q$对应的数值范围就是最好的数值范围。不巧的是，KL 散度需要两个直方图的 bin 是一样的 (L1 距离等也有这个要求)，而$Q$之前已经被量化到 128 个 bin 了。为了解决这个问题，需要把$Q$再反量化到跟$P$的 bin 数相同，这样就可以计算信息损失了。
5. 重复步骤 3、4，记录每次搜索的 KL 散度大小，直到搜索完整个范围。KL 散度最小的搜索范围，就是理论上信息损失最小的 minmax。

由于大部分情况下，数值分布都近似于正太分布 (即大部分数值会集中在一个区间内)，而随着搜索范围增大，离群点会越来越多，但中间那些真正有用的、比较集中的数值就只能用更少的 bin 来表达 (要知道总共只有 128 个 bin 可以承载信息)。因此，绝大部分情况下，舍弃离群点 (outlier) 获得的收益往往是更大的。
TRT的基本套路就是：从一个小的搜索范围逐渐扩大出去，每次搜索都量化一遍信息 (比如划分成固定 bin 数的直方图)，然后用一种度量方式 (KL 散度、L1 距离等) 来衡量完整信息和量化信息之间的差异，差异最小的区间就是我们需要的 minmax。

搜索$S$和$Z$

除了 minmax，也可以搜索合适的$S$和$Z$。这里的套路和前面是类似的，也是根据量化前后的信息损失来找出最优解。
假设量化前的浮点 weight 或 feature map 为向量$r$，那么量化后为：
$q=clip(round(\frac{r}{S}+Z)0,255)$
再进行反量化后得到：
$\hat{r}=S\ast (q-Z)=S\ast (clip(round(\frac{r}{S}+Z)0,255)-Z)$
接下来就可以度量量化的信息损失了，在论文 EasyQuant${}^2$中使用了余弦相似性，因此这里也以余弦相似性为例。
假设矫正数据集总共有$N$个样本，那么平均相似性为：
$\frac{1}{N}{\sum }_i^{N}cos(r_i,{\hat{r}}_i)=\frac{1}{N}{\sum }_i^N\frac{r_i{\hat{r}}_i}{||r_i||||{\hat{r}}_i||}$
而要求解的，就是使得这个相似性最大的$S$和$Z$(余弦相似性越大，信息损失越小)：
$\underset{S,Z}{\max }\frac{1}{N}{\sum }_i^N\frac{r_i{\hat{r}}_i}{||r_i||||{\hat{r}}_i||}$
搜索$S$和$Z$的方法有很多，比如可以参考前面 TRT 的思路，先设定$S$和$Z$的范围，然后我们用两个循环分别对$S$和$Z$进行搜索遍历，计算每一步搜索的相似性分数，分数最大的就是需要的$S$和$Z$。这种方法就是通常所说的Grid Search。

后训练量化——Data free quantization

论文：Data-Free Quantization Through Weight Equalization and Bias Correction
这篇论文的关键点是Data-Free(噱头，对feature量化的时候还是需要Data)、Weight Equalization、Bias Correction

Weight Equalization

MobileNet在per-layer 量化精度下降极其严重，只有用上 per-channel 的时候才能挽救一下。而 weight equalization 要做的事情，就是在使用 per-layer 量化的情况下，使用一些方法使得不同卷积核之间的数值分布能够均衡一些，让大家的数值分布都尽量接近，这样就可以用 per-layer 量化实现 per-channel 的精度 (毕竟 per-channel 实现上会比 per-layer 复杂一些)。

除了 weight 的问题之外，研究人员发现，模型量化的时候总是会产生一种误差，这种误差对数值分布的形态影响不大，但却会使整个数值分布发生偏移 (biased)。
假设有$N$个样本，那么对于 feature map 上面的每一个数值，我们可以用下面这种方式计算偏移误差 (biased error)：
$E[\widetilde{y_j}-y_j]\approx \frac{1}{N}({\sum }_n(\tilde{W}{x}_n{)}_j-(W{x}_n{)}_j)$
其中，$\tilde{W}$是量化后再反量化的 weight (即带了量化误差)，$W$是原先的 weight，$x_n$是输入，对应的$\widetilde{y_j}$是量化后的输出，$y_j$是原输出。
用这个公式可以算出引入量化误差后的 feature map 上每个点和原先的相差了多少，统计一下这些误差，就得到下面这张图：

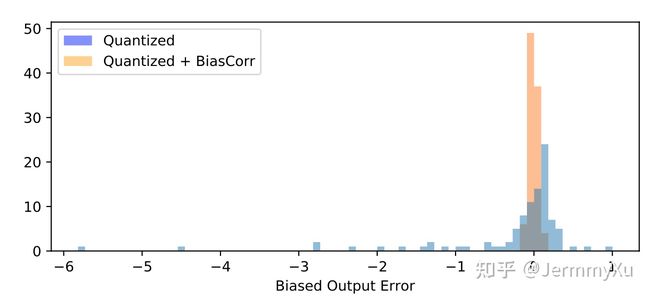
这里面蓝色的柱状图就统计了量化后的误差分布，看得出，有不少 feature 的误差已经超过了 1，而理想状态下，我们是希望量化后的误差能集中到 0 附近，越接近 0 越好，就像橙色直方图那样。
蓝色部分的分布状况是一种偏移(biased)。
研究人员发现，用上 weight equalization 后，这种 biased error 会更加地突出。而 Bias Correction 就是为了解决该问题提出的。

具体方法

要实现 Weight Equalization，一个很直接的想法就是对卷积核的每个 kernel (或者是全连接层的每个权重通道) 都乘上一个缩放系数，对数值范围大的 kernel 进行缩小，范围小的则扩大。

Positive scaling equivariance (伸缩等价)

卷积层和全连接层，本质上都是加权求和 (线性映射)，因此都满足下式：
$f(sx)=sf(x)$($s$必须是正数)

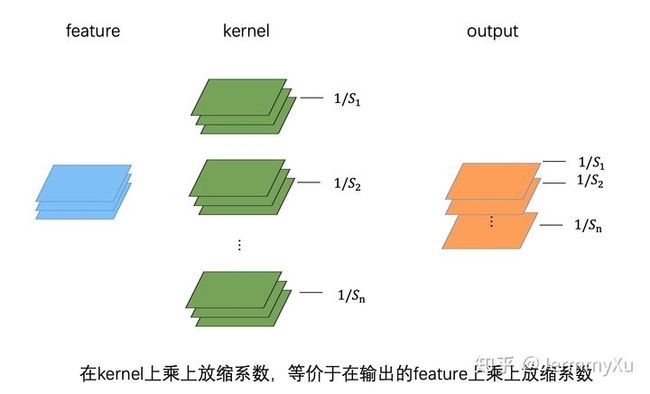
对于卷积来说，在卷积核上乘以放缩系数，等效于在输出上乘以同样的放缩系数。全连接层同理。(简单起见，上图中的 bias 被省略了)
如果卷积后跟着一个类 ReLU 的激活函数 (ReLU、LeakyReLU 等)，那么上式也是成立的，因为 ReLU 这类激活函数本质上也是分段线性的。
$ReLU(sx)=sReLU(x)$

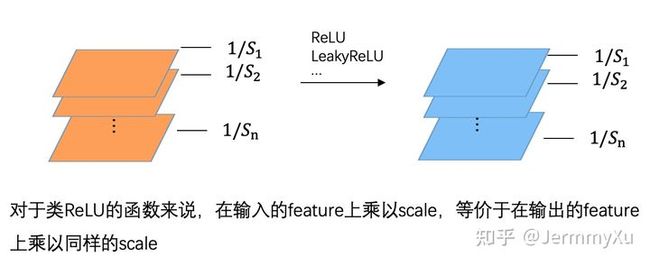
其实不只是 ReLU，任何分段线性的函数，都满足 Positive scaling equivariance。

有了以上这些性质后，就可以在下一个卷积核上乘以一个逆放缩系数，从而抵消第一个卷积核放缩的影响，实现计算上的等效性。

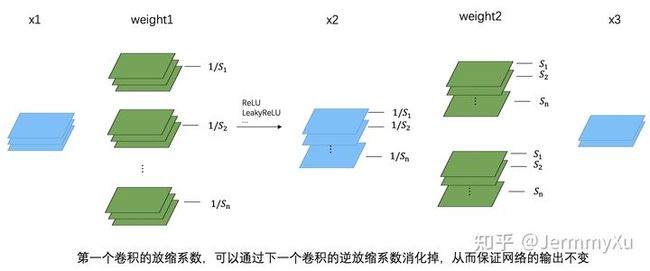
这一切成立的前提都在于 conv 和类 ReLU 函数满足公式$f(sx)=sf(x)$，从而可以把缩放系数等价地作用到下一层输入上，并进一步被下一层卷积的逆缩放系数吸收掉。需要注意的是，第一个卷积的缩放系数是乘在每个 kernel 上，而第二个卷积的逆缩放系数则是乘在每个 kernel 的 channel 上的。

这个过程总结一下就得到了论文中的公式：
$y=f(W^{(2)}f(W^{(1)}x+b^{(1)})+b^{(2)})$
$=f(W^{(2)}S\hat{f}(S^{-1}{W}^{(1)}x+S^{-1}{b}^{(1)})+b^{(2)})$
$=f({\hat{W}}^{(2)}\hat{f}({\hat{W}}^{(1)}x+{\hat{b}}^{(1)})+b^{(2)})$

如何找到放缩系数$S$

在 weight 上乘以$S$的目的是为了让不同 kernel 之间的数值尽可能相同，从而达到均衡化。为此，论文定义了一个指标来描述这种均衡化的程度 (称为均衡化系数)：
$p_i^{(1)}=\frac{r_i^{(1)}}{R^{(1)}}$
这里面，$r_i^{(1)}$表示第一个卷积核的第 i 个 kernel 的数值范围，$R^{(1)}$则表示第一个卷积核整体的数值范围。理想情况下，当然是每个 kernel 的数值范围都近似整个卷积核的数值范围 (即$p^{(1)}$的数值越大)，均衡化的程度越好。
不过，由于把缩放的代价转移到了下一个卷积核上了，因此，我同时要让这种代价越小越好。所以，对于下一个卷积核来说，它那些被缩放的权重也应该尽可能地均衡。
需要注意的是，在计算下一个卷积核的均衡化系数时，不能像第一个卷积核一样每个 kernel 单独计算，而应该把相同缩放系数的通道重新排列后，再按照前者的方式计算。(只是求解缩放系数的时候需要这么处理，正常卷积运算还是按照原来的卷积核来算)

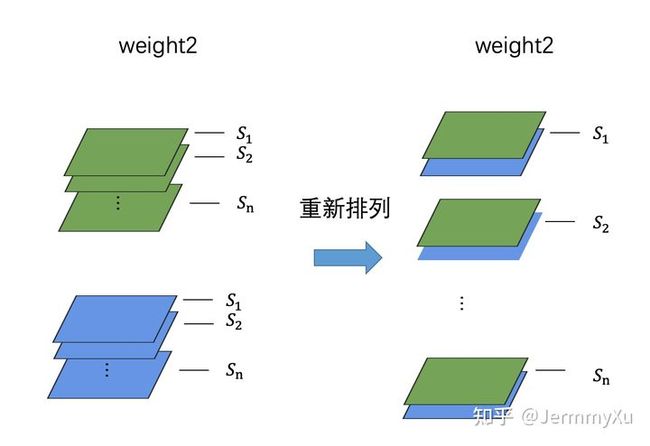
这种处理方法在数学优化以及代码实现上都能带来极大的方便。卷积核重新排列后，第二个卷积核的 kernel 数就和第一个相同了。
由此，论文给出了最终的优化函数：
$\underset{S}{\max }{\sum }_i{p}_i^{(1)}{p}_i^{(2)}$
这个式子翻译成人话就是，第一个卷积核和第二个卷积核 (重排后)，它们每个 kernel 的均衡化系数要尽可能大，而让所有 kernel 的系数之和最大的那个缩放系数$S$，就是我们想要的。
论文只针对对称量化求解这个函数，非对称量化结果也是一样的，具体求解过程在论文附录里面已经给出了。
这里直接给出最终的答案：
$s_i=\frac{1}{r_i^{(2)}}=\sqrt{r_i^{(1)}{r}_i^{(2)}}$
这就是每个 kernel 最优的放缩系数了。

Bias Correction

在上面提到，量化可能会破坏模型的数值分布，使得输出结果产生一个偏移 (biased)，因此需要对这个偏移做一点矫正。
假设原始全精度模型的权重是$W$，而带了量化误差的权重是 $\hat{W}$(这里的权重是将$W$进行量化后再反量化得到的)。由于 bias 量化引起的误差一般较小，一般不考虑，因此，可以大致估算出量化导致的误差偏移为：
$E[ϵx]=E[Wx]-E[\hat{W}x]=E[(W-\hat{W})x]$
$E[x]$表示从几个样本上计算得到的均值，又称期望，而$ϵ=W-\hat{W}$。
算出误差$E[x]$后，可以从卷积或者全连接层的 bias 里面减掉这个误差，这样一来，就通过 bias 把这个偏移抵消掉，因此把这种方法称为 bias correction。
在手头上有数据集的情况下，我们可以从数据集里面拿出$N$ 个样本，然后，分别跑一遍全精度模型和量化模型 (这里是量化后再反量化的权重，同时做了 weight equalization)，针对每一层输出，按照公式$E[ϵx]=E[(W-\hat{W})x]$计算出偏移后，再从对应层的 bias 上减掉这个偏移即可。需要注意的是，后面层在计算误差时，要等前面层已经做了 bias correction 后再进行，防止前面层已经矫正的偏移量传导到后面的层。
如果手头上没有数据，而网络里面刚好使用了 BatchNorm，那就又到了论文秀 Data-Free 的时间了。
根据期望的性质$E[ϵx]=ϵE[x]$，由于$ϵ$是可以根据权重计算的，因此只要知道$E[x]$，即输入的期望即可。那该如何在没有输入数据的情况下，得到输入的期望呢？论文假定，对于某一层 Conv 层，它的前一层跟着一个 BN 层和一个类 ReLU 的激活函数：

只要算出 ReLU 的输出的均值，那就相当于得到了所要求的 Conv 的输入均值$E[x]$。这里起关键作用的是 BN，BN 里面有两个参数：$\gamma$和$\beta$，它们表示 scale 和 shift，但同时它们还包含另一层物理意义，即方差和均值。换句话说，上面这幅图里面，$x^{pre}$的均值就是$\beta$。

所以，如果没有中间的 ReLU 函数的话，就可以直接用 BN 的参数$\beta$作为$E[x]$了。而如果 ReLU 存在的话，就需要考虑 ReLU 这类函数对数据分布的影响。论文在附录里面用了较大篇幅推出了 ReLU 后的均值：
$E[x_c]=E[ReLU(x_c^{pre})]={\gamma }_{c}N(\frac{-{\beta }_c}{{\gamma }_c})+{\beta }_c[1-\varphi ((\frac{-{\beta }_c}{{\gamma }_c})]$

量化训练之可微量化参数—LSQ

普通量化训练

在量化训练中需要加入伪量化节点 (Fake Quantize)，这些节点做的事情就是把输入的 float 数据量化一遍后，再反量化回 float，以此来模拟量化误差，同时在反向传播的时候，发挥 STE 的功能，把导数回传到前面的层。

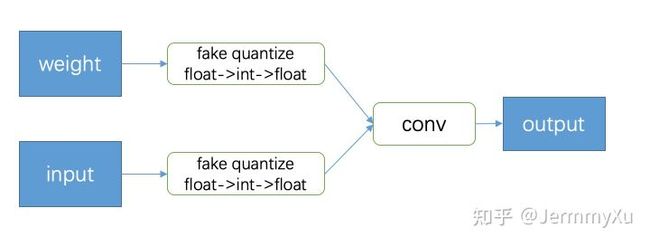
Fake Quantize 的过程可以总结成以下公式 (为了方便讲解 LSQ，这里采用 LSQ 中的对称量化的方式)：
$\bar{v}=round(clip(v/s,-Q_N,Q_p))$
$\hat{v}=\bar{v}\times s$
其中，$v$是 float 的输入，$\bar{v}$是量化后的数据 (仍然使用 float 来存储，但数值由于做了 round 操作，因此是整数)，\hat{v}是反量化的结果。$-Q_N$和$Q_P$分别是量化数值的最小值和最大值 (在对称量化中，$-Q_N$和$Q_P$通常是相等的)，$s$是量化参数。
由于 round 操作会带来误差，因此$\hat{v}$和$v$之间存在量化误差，这些误差反应到 loss 上会产生梯度，这样就可以反向传播进行学习。每次更新 weight 后，我们会得到新的 float 的数值范围，然后重新估计量化参数$s$:
$s=\frac{|v{|}_{max}}{Q_P}$

LSQ

LSQ 想做的，就是把这里的$s$也放到网络的训练当中，而不是通过权重来计算。(反向传播的时候对$s$求导进行更新)
$\hat{v}=round(clip(v/s.-Q_N,Q_P))\times s=\{\begin{array}{l}-Q_N\times s,v/s\le -Q_N\\ round(v/s)\times s,-Q_N<v/s<Q_P\\ Q_P\times s,v/s\ge Q_P\end{array}$
=>$\frac{\partial \hat{v}}{\partial s}=\{\begin{array}{l}-Q_N,v/s\le -Q_N\\ round(v/s)+\frac{\partial round(v/s)}{\partial s}\times s,-Q_N<v/s<-Q_P\\ Q_P,v/s\ge Q_P\end{array}$
$round(v/s)$这一步的导数可以通过 STE 得到：
$\frac{\partial round(v/s)}{\partial s}=\{\begin{array}{l}-Q_N,v/s\le -Q_N\\ -\frac{v}{s}+round(v/s),-Q_N<v/s<Q_P\\ Q_P,v/s\ge Q_P\end{array}$
在LSQ里，量化的时候采用对称量化，将zeropoint=0，初始化scale的方法为$s=\frac{2<|v|>}{\sqrt{Q_P}}$,$<\cdot >$代表均值。

LSQ+

LSQ+ 的思路和 LSQ 基本一致，就是把零点 (zero point，也叫 offset) 也变成可微参数进行训练，其中只有激活值(输入/输出)有zero point，weight没有zero point，并且参数初始化方法不一样
激活值:
$\bar{v}=round(clip(\frac{v-\beta }{s},-Q_N,Q_p))$
$\hat{v}=$