重参数 (Reparameterization)
Contents
- 基本概念
- 连续情形
- 离散情形
-
- Gumbel Max
- Gumbel Softmax
- Straight-Through Gumbel-Softmax Estimator
- 背后的故事: 梯度估计 (gradient estimator)
-
- SF 估计 (Score Function Estimator)
- 梯度方差
- 降方差
- References
基本概念
- 重参数 (Reparameterization) 实际上是处理如下期望形式的目标函数的一种技巧:
 上面的期望式可能在如下情形中出现 (e.g. VAE):假设我们在模型的前向传播过程中得到了随机变量 Z Z Z 的概率分布 p θ ( z ) p_\theta(z) pθ(z),其中 θ \theta θ 为模型参数,然后需要根据 p θ ( z ) p_\theta(z) pθ(z) 对随机变量 Z Z Z 进行采样,再根据采样得到的值 z z z 完成后续的前向传播过程,例如计算训练损失 f ( z ) f(z) f(z). 此时,训练损失 L θ L_\theta Lθ 即可写为上述期望的形式。然而,这里存在一个很大的问题,就是采样操作是不可导的,虽然我们可以完成模型的前向传播,但反向传播时却无法计算出梯度 ∂ L θ / ∂ θ \partial L_\theta/\partial \theta ∂Lθ/∂θ,也就无法进行模型的训练。而 Reparameterization 则是提供了一种变换,使得我们可以直接从 p θ ( z ) p_θ(z) pθ(z) 中采样,并且保留 θ θ θ 的梯度,也就是将采样操作由不可导变为可导
上面的期望式可能在如下情形中出现 (e.g. VAE):假设我们在模型的前向传播过程中得到了随机变量 Z Z Z 的概率分布 p θ ( z ) p_\theta(z) pθ(z),其中 θ \theta θ 为模型参数,然后需要根据 p θ ( z ) p_\theta(z) pθ(z) 对随机变量 Z Z Z 进行采样,再根据采样得到的值 z z z 完成后续的前向传播过程,例如计算训练损失 f ( z ) f(z) f(z). 此时,训练损失 L θ L_\theta Lθ 即可写为上述期望的形式。然而,这里存在一个很大的问题,就是采样操作是不可导的,虽然我们可以完成模型的前向传播,但反向传播时却无法计算出梯度 ∂ L θ / ∂ θ \partial L_\theta/\partial \theta ∂Lθ/∂θ,也就无法进行模型的训练。而 Reparameterization 则是提供了一种变换,使得我们可以直接从 p θ ( z ) p_θ(z) pθ(z) 中采样,并且保留 θ θ θ 的梯度,也就是将采样操作由不可导变为可导 - 重参数假设从分布 p θ ( z ) p_θ(z) pθ(z) 中采样可以分解为两个步骤:(1) 从无参数分布 q ( ε ) q(ε) q(ε) 中采样一个 ε ε ε;(2) 通过变换 z = g θ ( ε ) z=g_θ(ε) z=gθ(ε) 生成 z z z。那么,上述期望就变成了
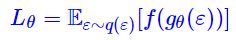 这时候被采样的分布就没有任何参数了,全部被转移到 f f f 内部了,因此可以采样若干个点,当成普通的 loss 那样写下来了 (上述重参数过程假定 p θ ( z ) = ∫ g θ ( ε ) = z q ( ε ) d ε = ∫ δ ( z − g θ ( ε ) ) q ( ε ) d ε p_θ(z)=∫_{g_θ(ε)=z}q(ε)dε=∫δ(z−g_θ(ε))q(ε)dε pθ(z)=∫gθ(ε)=zq(ε)dε=∫δ(z−gθ(ε))q(ε)dε, δ ( ⋅ ) δ(⋅) δ(⋅) 是狄拉克函数,因此有 L θ = E z ∼ p θ ( z ) [ f ( z ) ] = ∬ q ( ε ) δ ( z − g θ ( ε ) ) f ( z ) d ε d z = ∫ q ( ε ) f ( g θ ( ε ) ) d ε = E ε ∼ q ( ε ) [ f ( g θ ( ε ) ) ] L_\theta=\mathbb E_{z∼p_θ(z)}[f(z)]=\iint q(\varepsilon)\delta(z - g_{\theta}(\varepsilon)) f(z)d\varepsilon dz=\int q(\varepsilon) f(g_{\theta}(\varepsilon))d\varepsilon=\mathbb{E}_{\varepsilon\sim q(\varepsilon)}[f(g_{\theta}(\varepsilon))] Lθ=Ez∼pθ(z)[f(z)]=∬q(ε)δ(z−gθ(ε))f(z)dεdz=∫q(ε)f(gθ(ε))dε=Eε∼q(ε)[f(gθ(ε))])
这时候被采样的分布就没有任何参数了,全部被转移到 f f f 内部了,因此可以采样若干个点,当成普通的 loss 那样写下来了 (上述重参数过程假定 p θ ( z ) = ∫ g θ ( ε ) = z q ( ε ) d ε = ∫ δ ( z − g θ ( ε ) ) q ( ε ) d ε p_θ(z)=∫_{g_θ(ε)=z}q(ε)dε=∫δ(z−g_θ(ε))q(ε)dε pθ(z)=∫gθ(ε)=zq(ε)dε=∫δ(z−gθ(ε))q(ε)dε, δ ( ⋅ ) δ(⋅) δ(⋅) 是狄拉克函数,因此有 L θ = E z ∼ p θ ( z ) [ f ( z ) ] = ∬ q ( ε ) δ ( z − g θ ( ε ) ) f ( z ) d ε d z = ∫ q ( ε ) f ( g θ ( ε ) ) d ε = E ε ∼ q ( ε ) [ f ( g θ ( ε ) ) ] L_\theta=\mathbb E_{z∼p_θ(z)}[f(z)]=\iint q(\varepsilon)\delta(z - g_{\theta}(\varepsilon)) f(z)d\varepsilon dz=\int q(\varepsilon) f(g_{\theta}(\varepsilon))d\varepsilon=\mathbb{E}_{\varepsilon\sim q(\varepsilon)}[f(g_{\theta}(\varepsilon))] Lθ=Ez∼pθ(z)[f(z)]=∬q(ε)δ(z−gθ(ε))f(z)dεdz=∫q(ε)f(gθ(ε))dε=Eε∼q(ε)[f(gθ(ε))])
连续情形
- 简单起见,我们先考虑 z z z 为连续随机变量的情形:
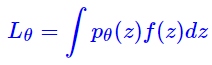 在 VAE 中常见的是正态分布 p θ ( z ) = N ( z ; μ θ , σ θ 2 ) p_{\theta}(z)=\mathcal{N}\left(z;\mu_{\theta},\sigma_{\theta}^2\right) pθ(z)=N(z;μθ,σθ2)
在 VAE 中常见的是正态分布 p θ ( z ) = N ( z ; μ θ , σ θ 2 ) p_{\theta}(z)=\mathcal{N}\left(z;\mu_{\theta},\sigma_{\theta}^2\right) pθ(z)=N(z;μθ,σθ2) - 总的来说,连续情形的重参数还是比较简单的。从数学本质来看,重参数是一种积分变换,即原来是关于 z z z 积分,通过 z = g θ ( ε ) z=g_θ(ε) z=gθ(ε) 变换之后得到新的积分形式。一个最简单的例子就是正态分布:对于正态分布来说,重参数就是 “从 N ( z ; μ θ , σ θ 2 ) N(z;μ_θ,σ^2_θ) N(z;μθ,σθ2) 中采样一个 z z z” 变成 “从 N ( ε ; 0 , 1 ) N(ε;0,1) N(ε;0,1) 中采样一个 ε ε ε,然后计算 ε × σ θ + μ θ ε×σ_θ+μ_θ ε×σθ+μθ”,所以
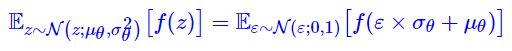
离散情形
- 为了突出 “离散”,我们将随机变量 z z z 换成 y y y,即对于离散情形要面对的目标函数是
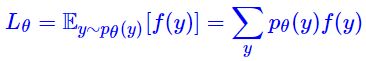 此时, p θ ( y ) p_\theta(y) pθ(y) 是一个 k k k 分类模型:
此时, p θ ( y ) p_\theta(y) pθ(y) 是一个 k k k 分类模型:
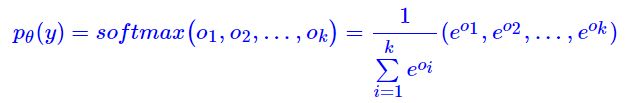
- 看到上述期望项中的求和,第一反应可能是 “求和?那就求呗,又不是求不了”。的确,对于离散的随机变量,其期望只不过是有限项求和,理论上确实可以直接完成求和再去梯度下降。但是,如果 k k k 特别大呢?举个例子,假设 y y y 是一个 100 维的向量,每个元素不是 0 就是 1,那么所有不同的 y y y 的总数目就是 2 100 2^{100} 2100,要对这样的 2 100 2^{100} 2100 个单项进行求和,计算量是难以接受的 (每一项都需要计算前向传播过程 f ( y ) f(y) f(y))。所以,还是需要回到采样上去,如果能够采样若干个点就能得到期望的有效估计,并且还不损失梯度信息,那自然是最好了
Gumbel Max
- 为此,需要先引入 Gumbel Max。假设每个类别的概率是 p 1 , p 2 , … , p k p_1,p_2,…,p_k p1,p2,…,pk,那么 Gumbel Max 提供了一种依概率采样类别的方案:
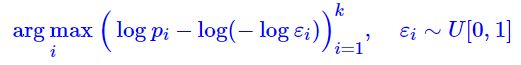 也就是说,先算出各个概率的对数 log p i \log p_i logpi,然后从均匀分布 U [ 0 , 1 ] U[0,1] U[0,1] 中采样 k k k 个随机数 ε 1 , … , ε k ε_1,…,ε_k ε1,…,εk,把 g i = − log ( − log ε i ) ∼ Gumbel(0,1) g_i=−\log(−\log ε_i)\sim\text{Gumbel(0,1)} gi=−log(−logεi)∼Gumbel(0,1) 加到 log p i \log p_i logpi 上去,最后把最大值对应的类别抽取出来就行了。由于现在的随机性已经转移到 U [ 0 , 1 ] U[0,1] U[0,1] 上去了,并且 U [ 0 , 1 ] U[0,1] U[0,1] 不带有未知参数,因此 Gumbel Max 就是离散分布的一个重参数过程
也就是说,先算出各个概率的对数 log p i \log p_i logpi,然后从均匀分布 U [ 0 , 1 ] U[0,1] U[0,1] 中采样 k k k 个随机数 ε 1 , … , ε k ε_1,…,ε_k ε1,…,εk,把 g i = − log ( − log ε i ) ∼ Gumbel(0,1) g_i=−\log(−\log ε_i)\sim\text{Gumbel(0,1)} gi=−log(−logεi)∼Gumbel(0,1) 加到 log p i \log p_i logpi 上去,最后把最大值对应的类别抽取出来就行了。由于现在的随机性已经转移到 U [ 0 , 1 ] U[0,1] U[0,1] 上去了,并且 U [ 0 , 1 ] U[0,1] U[0,1] 不带有未知参数,因此 Gumbel Max 就是离散分布的一个重参数过程 - 可以证明,这样的过程精确等价于依概率 p 1 , p 2 , … , p k p_1,p_2,…,p_k p1,p2,…,pk 采样一个类别,换句话说,在 Gumbel Max 中,输出 i i i 的概率正好是 p i p_i pi. 不失一般性,这里我们证明输出 1 的概率是 p 1 p_1 p1. 注意,输出 1 意味着 log p 1 − l o g ( − l o g ε 1 ) \log p_1−log(−logε_1) logp1−log(−logε1) 是最大的,这又意味着:
log p 1 − log ( − log ε 1 ) > log p 2 − log ( − log ε 2 ) log p 1 − log ( − log ε 1 ) > log p 3 − log ( − log ε 3 ) ⋮ log p 1 − log ( − log ε 1 ) > log p k − log ( − log ε k ) \begin{aligned} &\log p_1 - \log(-\log \varepsilon_1) > \log p_2 - \log(-\log \varepsilon_2) \\ &\log p_1 - \log(-\log \varepsilon_1) > \log p_3 - \log(-\log \varepsilon_3) \\ &\qquad \vdots\\ &\log p_1 - \log(-\log \varepsilon_1) > \log p_k - \log(-\log \varepsilon_k) \end{aligned} logp1−log(−logε1)>logp2−log(−logε2)logp1−log(−logε1)>logp3−log(−logε3)⋮logp1−log(−logε1)>logpk−log(−logεk)不失一般性,我们只分析第一个不等式,化简后得到:
ε 2 < ε 1 p 2 / p 1 ≤ 1 \varepsilon_2 < \varepsilon_1^{p_2 / p_1}\leq 1 ε2<ε1p2/p1≤1由于 ε 2 ∼ U [ 0 , 1 ] ε_2∼U[0,1] ε2∼U[0,1],所以 ε 2 < ε 1 p 2 / p 1 ε_2<ε^{p_2/p_1}_1 ε2<ε1p2/p1 的概率就是 ε 1 p 2 / p 1 ε^{p_2/p_1}_1 ε1p2/p1,这就是固定 ε 1 ε_1 ε1 的情况下,第一个不等式成立的概率。那么,所有不等式同时成立的概率是
ε 1 p 2 / p 1 ε 1 p 3 / p 1 … ε 1 p k / p 1 = ε 1 ( p 2 + p 3 + ⋯ + p k ) / p 1 = ε 1 ( 1 / p 1 ) − 1 \varepsilon_1^{p_2 / p_1}\varepsilon_1^{p_3 / p_1}\dots \varepsilon_1^{p_k / p_1}=\varepsilon_1^{(p_2 + p_3 + \dots + p_k) / p_1}=\varepsilon_1^{(1/p_1)-1} ε1p2/p1ε1p3/p1…ε1pk/p1=ε1(p2+p3+⋯+pk)/p1=ε1(1/p1)−1然后对所有 ε 1 ε_1 ε1 求平均,就是
∫ 0 1 ε 1 ( 1 / p 1 ) − 1 d ε 1 = p 1 \int_0^1 \varepsilon_1^{(1/p_1)-1}d\varepsilon_1 = p_1 ∫01ε1(1/p1)−1dε1=p1
Gumbel Softmax
- 我们希望重参数不丢失梯度信息,但是 Gumbel Max 做不到,因为 arg max \argmax argmax 不可导,为此,需要做进一步的近似。首先,留意到在神经网络中,处理离散输入的基本方法是转化为 one hot 形式,包括 Embedding 层的本质也是 one hot 全连接,因此 arg max \argmax argmax 实际上是 one_hot ( arg max ) \text{one\_hot}(\argmax) one_hot(argmax),然后,我们寻求 one_hot ( arg max ) \text{one\_hot}(\argmax) one_hot(argmax) 的光滑近似,它就是 s o f t m a x softmax softmax. 由此,我们得到 Gumbel Max 的光滑近似版本——Gumbel Softmax:
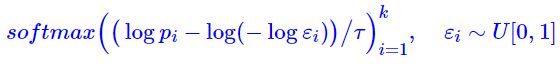 其中参数 τ > 0 τ>0 τ>0 称为退火参数,它越小输出结果就越接近 one hot 形式 (但同时梯度消失就越严重)。提示一个小技巧,如果 p i p_i pi 是 s o f t m a x softmax softmax 的输出,那么大可不必先算出 p i p_i pi 再取对数,直接将 log p i \log p_i logpi 替换为 o i o_i oi 即可:
其中参数 τ > 0 τ>0 τ>0 称为退火参数,它越小输出结果就越接近 one hot 形式 (但同时梯度消失就越严重)。提示一个小技巧,如果 p i p_i pi 是 s o f t m a x softmax softmax 的输出,那么大可不必先算出 p i p_i pi 再取对数,直接将 log p i \log p_i logpi 替换为 o i o_i oi 即可:
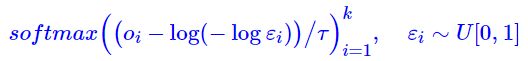
- 跟连续情形一样,Gumbel Softmax 就是用在需要求 E y ∼ p θ ( y ) [ f ( y ) ] \mathbb{E}_{y\sim p_{\theta}(y)}[f(y)] Ey∼pθ(y)[f(y)]、且无法直接完成对 y y y 求和的场景,这时候我们算出 p θ ( y ) p_θ(y) pθ(y)(或者 o i o_i oi),然后选定一个 τ > 0 τ>0 τ>0,用 Gumbel Softmax 算出一个随机向量来 y ~ \tilde y y~,代入计算得到 f ( y ~ ) f(\tilde y) f(y~),它就是 E y ∼ p θ ( y ) [ f ( y ) ] \mathbb{E}_{y\sim p_{\theta}(y)}[f(y)] Ey∼pθ(y)[f(y)] 的一个好的近似,且保留了梯度信息
- 注意,Gumbel Softmax 不是类别采样的等价形式,Gumbel Max 才是。而 Gumbel Max 可以看成是 Gumbel Softmax 在 τ → 0 τ→0 τ→0 时的极限。当 τ τ τ 比较小时,Gumbel Softmax 采样得到的样本接近 one-hot vector,也就比较接近实际的采样情况,但梯度的方差比较大;当 τ τ τ 比较大时,Gumbel Softmax 采样得到的样本比较平滑 (一个平滑的概率向量,向量的各个分量的值都差不多),但梯度的方差比较小。所以在应用 Gumbel Softmax 时,开始可以选择较大的 τ τ τ(比如 1),然后慢慢退火到一个接近于 0 的数(比如 0.01),这样才能得到比较好的结果
Gumbel Softmax v.s. Softmax
- Gumbel Softmax 通过 τ → 0 τ→0 τ→0 的退火来逐渐逼近 one hot,相比直接用原始的 Softmax 进行退火,区别在于原始 Softmax 退火只能得到最大值位置为 1 的 one hot 向量,而 Gumbel Softmax 有概率得到非最大值位置的 one hot 向量,增加了随机性,会使得基于采样的训练更充分一些
Straight-Through Gumbel-Softmax Estimator
- 由 Gumbel Softmax 得到的采样样本是实际采样样本的一个近似,它甚至都不在离散变量的取值范围之内,即使 τ τ τ 比较小,Gumbel Softmax 采样得到的样本也只是接近 one-hot vector,而非真正离散化的 one-hot vector. 但总存在那么一些场景,我们只想采样离散值而非连续值 (e.g. RL 中从离散的动作空间中采样)
- 假设 Gumbel Softmax 输出的采样向量为 y y y,为了利用 Gumbel Softmax 采样离散值,我们可以在前向传播时使用 z = one_hot ( arg max y ) z=\text{one\_hot}(\argmax y) z=one_hot(argmaxy) 得到离散的采样值,在反向传播时利用 ∇ θ z ≈ ∇ θ y \nabla_\theta z\approx \nabla_\theta y ∇θz≈∇θy,对 ∇ θ y \nabla_\theta y ∇θy 进行梯度回传:
z = y + s g ( one_hot ( arg max y ) − y ) z=y+sg(\text{one\_hot}(\argmax y)-y) z=y+sg(one_hot(argmaxy)−y)其中, s g sg sg 为 stop gradient 操作
背后的故事: 梯度估计 (gradient estimator)
- 重参数就这样介绍完了吗?远远没有,重参数的背后,实际上是一个称为 “梯度估计”的 大家族,而重参数只不过是这个大家族中的一员。每年的 ICLR、ICML 等顶会上搜索gradient estimator、REINFORCE 等关键词,可以搜索到不少文章,说明这是个大家还在钻研的课题。要想说清重参数的来龙去脉,也要说些梯度估计的故事
SF 估计 (Score Function Estimator)
- 前面我们分别讲了连续型和离散型的重参数,都是在 “loss 层面” 讲述的,也就是说都是想办法把 loss 显式地定义好,剩下的交给框架自动求导、自动优化就是了。而事实上,就算不能显式地写出 loss 函数,也不妨碍我们对它求导,自然也不妨碍我们去用梯度下降了。比如 Score Function Estimator:
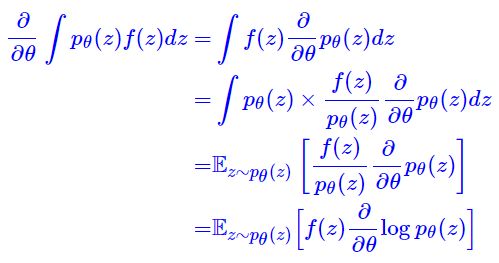 这是对原来损失函数的最朴素的估计,在强化学习中 z z z 代表着策略,那么上式就是一个最基本的策略梯度,所以有时候也直接称上述估计为叫 REINFORCE。现在我们可以直接从 p θ ( z ) p_θ(z) pθ(z) 中采样若干个点来估算 ∂ L θ / ∂ θ \partial L_\theta/\partial \theta ∂Lθ/∂θ 的值了,不用担心会不会没梯度
这是对原来损失函数的最朴素的估计,在强化学习中 z z z 代表着策略,那么上式就是一个最基本的策略梯度,所以有时候也直接称上述估计为叫 REINFORCE。现在我们可以直接从 p θ ( z ) p_θ(z) pθ(z) 中采样若干个点来估算 ∂ L θ / ∂ θ \partial L_\theta/\partial \theta ∂Lθ/∂θ 的值了,不用担心会不会没梯度 - 同时注意到,重参数技巧要求 f f f 可导,但是在诸如强化学习的场景下, f ( z ) f(z) f(z) 对应着奖励函数,很难做到光滑可导,此时就必须使用 SF 估计
梯度方差
- SF 估计看上去很美好,得到了一个连续和离散变量都适用的估计式,那为什么还需要重参数呢?主要的原因是:SF 估计的方差太大。SF 估计是函数 f ( z ) ∂ ∂ θ log p θ ( z ) f(z) \frac{\partial}{\partial\theta} \log p_{\theta}(z) f(z)∂θ∂logpθ(z) 在分布 p θ ( z ) p_θ(z) pθ(z) 下的期望,我们要采样几个点来算 (理想情况下,希望只采样一个点),换句话说,我们想用下面的近似
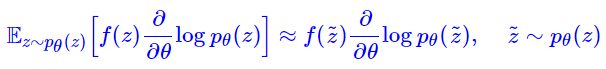 于是问题就来了:这样的梯度估计方差很大,这导致了我们用梯度下降优化的时候相当不稳定,非常容易崩
于是问题就来了:这样的梯度估计方差很大,这导致了我们用梯度下降优化的时候相当不稳定,非常容易崩
降方差
- 重参数就是一种降方差技巧,为此,我们写出重参数后的梯度表达式:
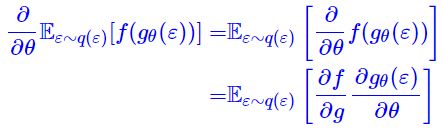 对比 SF 估计,我们可以直观感知为什么上式方差更小了 (只是一般情况下,并不是绝对成立):(1) SF 估计中包含了 log p θ ( z ) \log p_θ(z) logpθ(z),我们知道,作为一个合理的概率分布,一般都在无穷远处 (即 ∥ z ∥ → ∞ ∥z∥→∞ ∥z∥→∞)都会有 p θ ( z ) → 0 p_θ(z)→0 pθ(z)→0,取了 log \log log 之后反而会趋于负无穷,换句话说, log p θ ( z ) \log p_θ(z) logpθ(z) 这一项实际上放大了无穷远处的波动,从而一定程度上增加了方差;(2) SF 估计中包含的是 f f f 而重参数之后变成了 ∂ f / ∂ g ∂f/∂g ∂f/∂g, f f f 一般是神经网络,而通常我们定义的神经网络模型其实都是 O ( z ) \mathscr O(z) O(z) 级别的模型,从而我们可以预期它的梯度是 O ( 1 ) \mathscr O(1) O(1) 级别的(不严格成立,只能说在平均意义下基本成立),所以相对情况下更平稳一些,因此 f f f 的方差也比 ∂ f / ∂ g ∂f/∂g ∂f/∂g 的方差要大
对比 SF 估计,我们可以直观感知为什么上式方差更小了 (只是一般情况下,并不是绝对成立):(1) SF 估计中包含了 log p θ ( z ) \log p_θ(z) logpθ(z),我们知道,作为一个合理的概率分布,一般都在无穷远处 (即 ∥ z ∥ → ∞ ∥z∥→∞ ∥z∥→∞)都会有 p θ ( z ) → 0 p_θ(z)→0 pθ(z)→0,取了 log \log log 之后反而会趋于负无穷,换句话说, log p θ ( z ) \log p_θ(z) logpθ(z) 这一项实际上放大了无穷远处的波动,从而一定程度上增加了方差;(2) SF 估计中包含的是 f f f 而重参数之后变成了 ∂ f / ∂ g ∂f/∂g ∂f/∂g, f f f 一般是神经网络,而通常我们定义的神经网络模型其实都是 O ( z ) \mathscr O(z) O(z) 级别的模型,从而我们可以预期它的梯度是 O ( 1 ) \mathscr O(1) O(1) 级别的(不严格成立,只能说在平均意义下基本成立),所以相对情况下更平稳一些,因此 f f f 的方差也比 ∂ f / ∂ g ∂f/∂g ∂f/∂g 的方差要大
References
- 苏剑林. (Jun. 10, 2019). 《漫谈重参数:从正态分布到 Gumbel Softmax 》[Blog post]. Retrieved from https://kexue.fm/archives/6705
- Gumbel Softmax paper: Jang, Eric, et al. “Categorical Reparameterization with Gumbel-Softmax.” 5th International Conference on Learning Representations, ICLR 2017