统计学习方法(李航) 支持向量机 附python及sklearn实现

支持向量机

• 有监督学习
• 分类问题
• $Vapnik$
• 线性可分支持向量机/线性支持向量机/非线性支持向量机

什么是支持向量机呢？

$SupportVectorMachine$：支持向量机

先抛出难懂的定义～可以先跳过，最后再来回顾

定义：支持向量机的基本模型是定义在特征空间上的间隔最大的线性分类器。支持向量机还包括核技巧，这使得它成为实质上的非线性分类器。支持向量机的学习策略即间隔最大化，可以形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。支持向量机的学习算法是求解凸二次规划的最优化问题。

支持向量机的学习方法由简至繁：

• 线性可分支持向量机$(linearsupportvectormachineinlinearlyseparablecase)$
• 线性支持向量机$(linearsupportvectormachine)$
• 非线性支持向量机$(non-linearsupportvectormachine)$

根据训练数据：

• 当训练数据线性可分时，通过硬间隔最大化$(hardmarginmaximization)$，学习一个线性的分类器，即线性可分支持向量机，又称为硬间隔支持向量机

• 当训练数据近似可分时，通过软间隔最大化$(softmarginmaximization)$，学习一个线性的分类器，即线性支持向量机，又称为软间隔支持向量机

• 当训练数据不可分时，通过核技巧$(kerneltrick)$，学习非线性支持向量机

1.初步了解，当数据是线性可分时

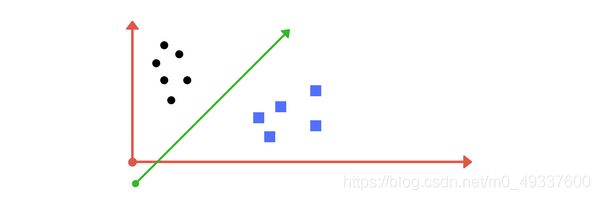
假设现在二维平面上有两组不同标签的数据，你能够区分这两组数据吗？

你可能已经能够想出类似与下方图片的划分方法。很显然，在绿线左边的是黑色的类，而右边的是蓝色的类。

这就是$SVM$做的事情（在多维平面上分离各组类），它能够找到一个超平面（此处为直线），有效的将两组类区分。绿色的直线即为我们找到的支持向量的分类器。当然这种划分方式也称作为硬间隔，因为我们不允许有训练数据出现错误分类的情况～

2.那么，假如数据是近似可分的呢？

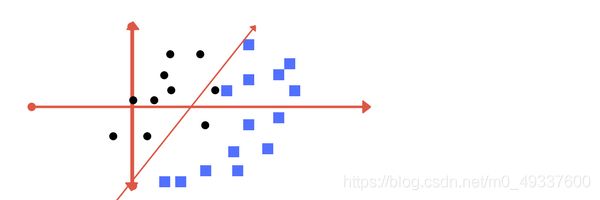
那么，我们再来观察一组数据，假如数据重叠了或则黑色的点出现在了蓝色的点中，我们该如何辨别呢？

观察下方的两种超平面的画法，我们该选择哪一种？

第一种划分：

第二种划分：

答案是：两种都正确，第一种我们容忍了误分类点的存在即这种间隔我们称为软间隔，而第二种则是期望达到0误差点，这种间隔我们称为硬间隔。

3.进一步复杂情况，当数据是线性不可分时

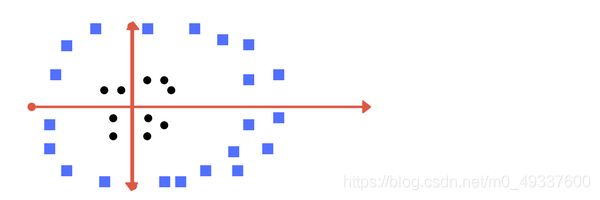
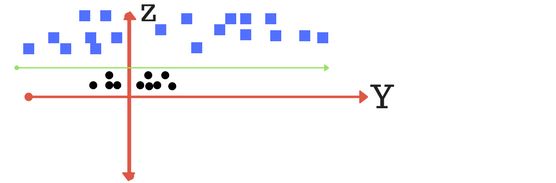
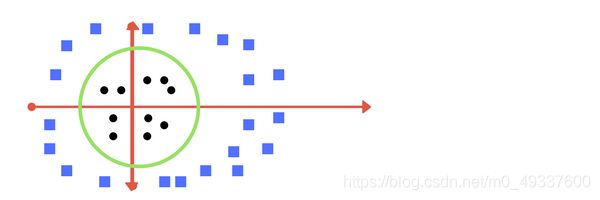
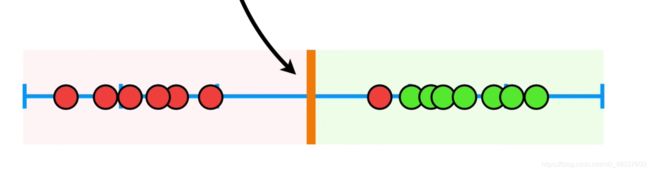
那么接下来我们来看另一组数据，显然在x-y系平面上数据时线性不可分的，那么我们该如何做呢？

我们的解决方式是增加一个维度（即我们现在将数据放置于x-y-z系），我们将它记为z轴，假设$z=x^2+y^2$。并变换到z-y系下。在这种情况下，我们可以轻松地找到一个超平面将数据有效的区分为两组类。

当我们再变换回x-y系，超平面将以圆的形式展现出来。绿色的圆即为我们找到的支持向量的分类器。

嗯嗯…什么硬间隔，软间隔，超平面，核技巧…是不是还雨里雾里的？接下来我们继续用例子来说明这些术语的含义！

支持向量机中的术语

在这节，我们将讨论以下术语：

• Margin（间隔）

• Support vector（支持向量）

• Hyperplane（超平面）

• Kernels（核）

• Regularization（正则化）

• Gamma

Margin

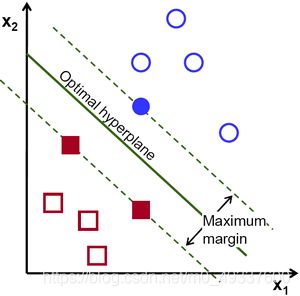
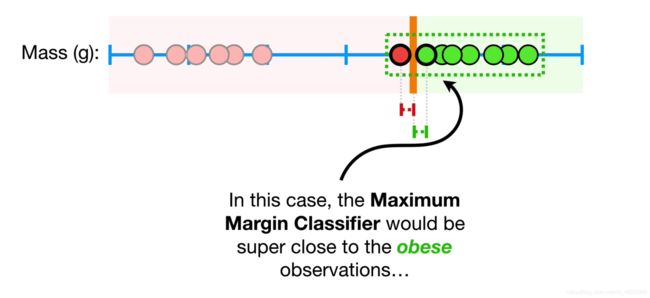
在2维平面上，我们能够找到许多区分两个类的点的超平面（此处为直线），例如下图所示的绿线，但我们选取超平面的准则是什么呢？

我们的目标是找到一个具有最大化间隔（Margin）的超平面。这里我们称距离超平面最近的点为支持向量（绿色虚线上的点）。当然，这里准确的来说应该称作硬间隔，因为不存在误分类的点～

在了解硬间隔和软间隔之前，我们先来了解一下支持向量～

Support Vector

支持向量是距离超平面最近的点，并且它会影响超平面的位置和方向，改变支持向量会改变超平面的位置。利用这些支持向量，我们可以最大化间隔。这些点将帮助我们建立$SVM$模型。

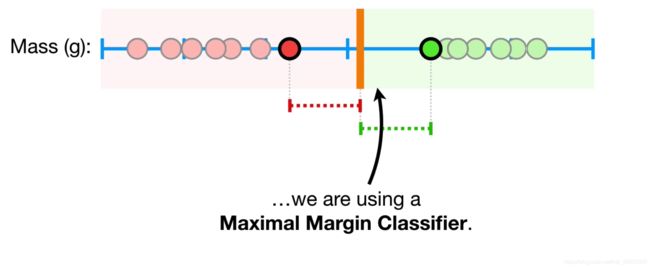
接下来我们谈谈硬间隔和软间隔的区别吧～观察下面这张图，当训练数据是线性可分的

我们通过支持向量，找到间隔最大的地方，我们称此时的间隔为最大间隔，即

因为此时训练数据没有误分类的点，故称为硬间隔。

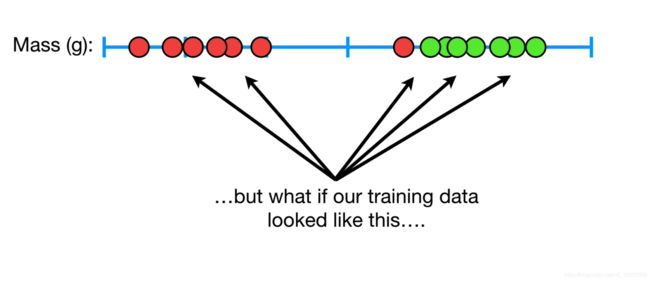
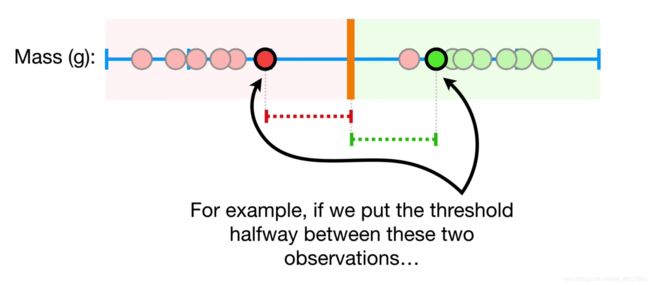
再观察下面这张图，当数据依旧使用最大间隔划分时

我们清楚地发现，此时最大间隔的方法并不适合这种情况，因为红色的点显然更倾向于绿色，但我们却将它分类为红色。

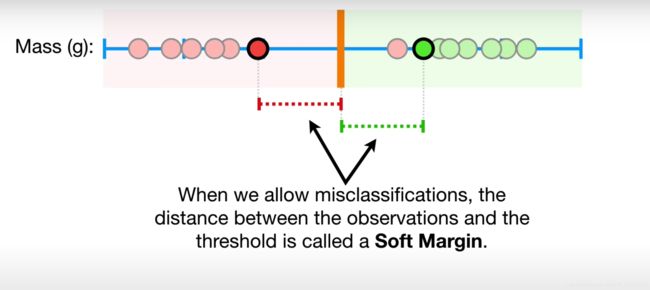
那么，我们该如何做呢？如果我们把间隔置于下图所示，即允许存在误分类的点

那么此时我们称这种方法为软间隔

Hyperplane

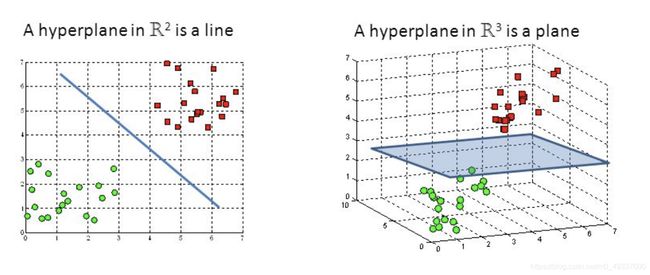
超平面是决策边界，将帮助我们区分数据点。数据落于超平面的两侧将被区分为不同的类别。当然，数据样本的特征数量将决定超平面的维度，比如特征数量为2时，超平面是直线；特征数量是3时，超平面变成了2维的平面；然而，当特征数量大于3时，我们很难在空间上想象它的形状。

Kernels

核函数$(kernelfunction)$系统地在更高维度上找到线性分类器

1.多项式核$(PolynomialKernel)$

• 参数d，代表了多元函数的维度
• $K(x,x_i)=(x\cdot x_i+1{)}^d$

1.1当d=1时，多元核在1-维度上计算样本点间的距离

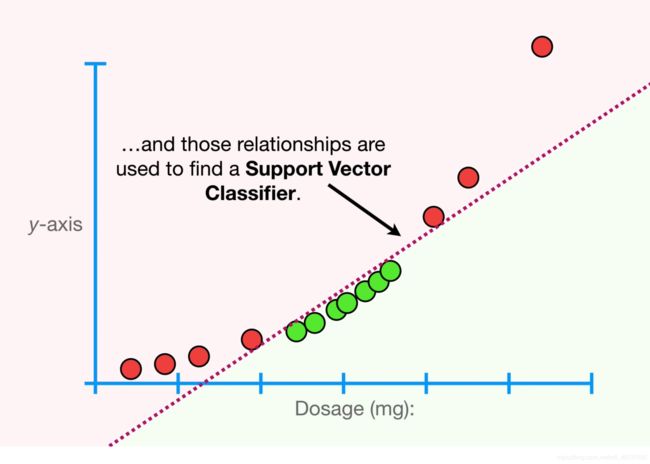
这将有助于我们找到支持向量的分类器，即

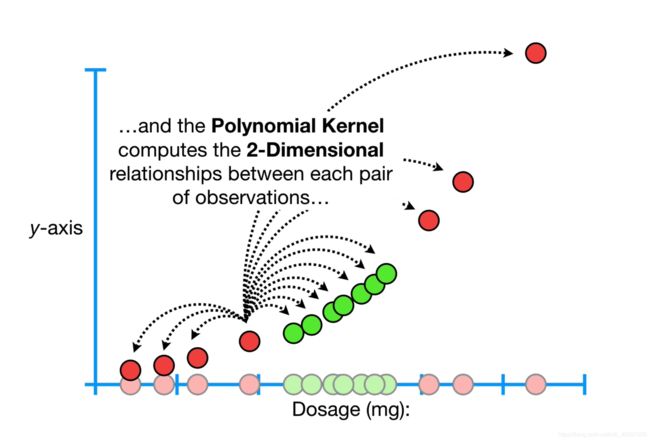
1.2当d=2时，即先将x轴上的映射至y轴，即$y=x^2$，多元核在2-维度上计算样本点间的距离

这将有助于我们找到支持向量的分类器，即

1.3当d=3时，多元核在3-维度上计算样本点间的距离

这将有助于我们找到支持向量的分类器，即

当d大于或则等于4的时，我们将在更高的维度即超平面上找到支持向量机的分类器

总结，多元核通过增加维度，样本点间的关系将助力我们寻找支持向量的分类器，当然，我们还可以借助交叉验证来寻找最优的参数d

2.高斯径向基函数核$(RadialBasisKernel)$

• 简称$RBK$
• $K(x,x_i)=exp(-\frac{||x-x_i|{|}_2^2}{2{\sigma }^2})$

很遗憾，$RBK$是通过提升至无限维度来寻找支持向量分类器，我们将不能清楚地看到直观的例子

!!!注意

实际上，我们并没有将数据映射至高维度，而是直接在高维度上进行计算，这种技巧称为$KernelTrick$

Regularization

正则化参数（在$Scikit-learn$中参数一般为$C$），将会告诉$SVM$优化器模型需要避免多少误分类对于每一组训练样本。

对于较大值的$C$，优化将优先选择一个较小间隔的超平面。 相反，导致优化器寻找较大的间隔分隔超平面，即使该超平面对更多点进行了错误分类。

第一种分类方式即是$C$值较低的结果：

第二种分类方式即是$C$值较高的结果：

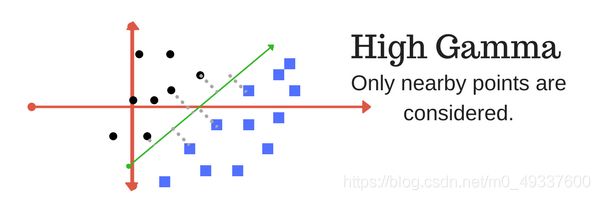
Gamma

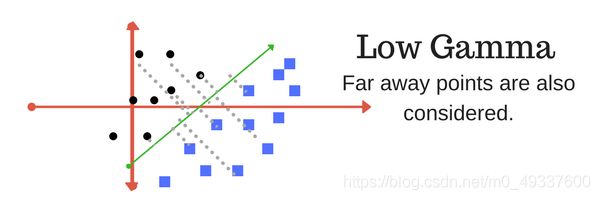
$\gamma$参数定义了每个样本点在距离上的影响力，换句话说，较低的$\gamma$值在计算划分时应考虑远离划分线的点，而较高的$\gamma$值将会考虑接近划分线的点。

让我们来使用支持向量机对鸢尾花品种的辨别

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.utils import shuffle

%matplotlib inline
%config InlineBackend.figure_format='svg'

# 加载鸢尾花数据

iris = load_iris()
df = pd.DataFrame(iris.data,columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
df.head()

x = df['sepal length']
y = df['petal width']

setosa_x = x[:50]
setosa_y = y[:50]

versicolor_x = x[50:]
versicolor_y = y[50:]

#	数据可视化

plt.figure(figsize=(8,6))
plt.scatter(setosa_x,setosa_y,marker='+',color='green')
plt.scatter(versicolor_x,versicolor_y,marker='_',color='red')
plt.tick_params(direction='in')
plt.show()

df = df.drop(['sepal width','petal length'],axis = 1)

Y =df['label']

df = df.drop(['label'],axis=1)

X = df.values.tolist()

# 打乱数据

X,Y = shuffle(X,Y)

x_train = []
y_train = []
x_test = []
y_test = []

# 划分数据
x_train, x_test, y_train, y_test = train_test_split(X, Y, train_size=0.9)

x_train = np.array(x_train)
y_train = np.array(y_train)
x_test = np.array(x_test)
y_test = np.array(y_test)

from sklearn.svm import SVC
from sklearn.metrics import accuracy_score

# sklearn-svm

clf = SVC(kernel='linear')
clf.fit(x_train,y_train)
y_pred = clf.predict(x_test)
print(accuracy_score(y_test,y_pred))

或则我们用Python来手写一个SVM分类器

1.导入相关库

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import  train_test_split
import matplotlib.pyplot as plt

%matplotlib inline
%config InlineBackend.figure_format = 'svg'

2.定义数据集

# 加载鸢尾花数据

def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = [
        'sepal length', 'sepal width', 'petal length', 'petal width', 'label'
    ]
    data = np.array(df.iloc[:100, [0, 1, -1]])
    for i in range(len(data)):
        if data[i, -1] == 0:
            data[i, -1] = -1
    # print(data)
    return data[:, :2], data[:, -1]
  
X, y = create_data()

# 划分数据
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)

3.可视化数据

plt.scatter(X[:50,0],X[:50,1], label='0',c = '',edgecolors = 'green')
plt.scatter(X[50:,0],X[50:,1], label='1',c = '',edgecolors = 'blue')
plt.tick_params(direction = 'in')
plt.legend()

4.定义SVM

class SVM:
    def __init__(self, max_iter=100, kernel='linear'):
        self.max_iter = max_iter
        self._kernel = kernel

    def init_args(self, features, labels):
        self.m, self.n = features.shape
        self.X = features
        self.Y = labels
        self.b = 0.0

        # 将Ei保存在一个列表里
        self.alpha = np.ones(self.m)
        self.E = [self._E(i) for i in range(self.m)]
        # 松弛变量
        self.C = 1.0

    def _KKT(self, i):
        y_g = self._g(i) * self.Y[i]
        if self.alpha[i] == 0:
            return y_g >= 1
        elif 0 < self.alpha[i] < self.C:
            return y_g == 1
        else:
            return y_g <= 1

    # g(x)预测值，输入xi（X[i]）
    def _g(self, i):
        r = self.b
        for j in range(self.m):
            r += self.alpha[j] * self.Y[j] * self.kernel(self.X[i], self.X[j])
        return r

    # 核函数
    def kernel(self, x1, x2):
        if self._kernel == 'linear':
            return sum([x1[k] * x2[k] for k in range(self.n)])
        elif self._kernel == 'poly':
            return (sum([x1[k] * x2[k] for k in range(self.n)]) + 1)**2

        return 0

    # E（x）为g(x)对输入x的预测值和y的差
    def _E(self, i):
        return self._g(i) - self.Y[i]

    def _init_alpha(self):
        # 外层循环首先遍历所有满足0
        index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
        # 否则遍历整个训练集
        non_satisfy_list = [i for i in range(self.m) if i not in index_list]
        index_list.extend(non_satisfy_list)

        for i in index_list:
            if self._KKT(i):
                continue

            E1 = self.E[i]
            # 如果E2是+，选择最小的；如果E2是负的，选择最大的
            if E1 >= 0:
                j = min(range(self.m), key=lambda x: self.E[x])
            else:
                j = max(range(self.m), key=lambda x: self.E[x])
            return i, j

    def _compare(self, _alpha, L, H):
        if _alpha > H:
            return H
        elif _alpha < L:
            return L
        else:
            return _alpha

    def fit(self, features, labels):
        self.init_args(features, labels)

        for t in range(self.max_iter):
            # train
            i1, i2 = self._init_alpha()

            # 边界
            if self.Y[i1] == self.Y[i2]:
                L = max(0, self.alpha[i1] + self.alpha[i2] - self.C)
                H = min(self.C, self.alpha[i1] + self.alpha[i2])
            else:
                L = max(0, self.alpha[i2] - self.alpha[i1])
                H = min(self.C, self.C + self.alpha[i2] - self.alpha[i1])

            E1 = self.E[i1]
            E2 = self.E[i2]
            # eta=K11+K22-2K12
            eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(
                self.X[i2],
                self.X[i2]) - 2 * self.kernel(self.X[i1], self.X[i2])
            if eta <= 0:
                # print('eta <= 0')
                continue

            alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (
                E1 - E2) / eta  #此处有修改，根据书上应该是E1 - E2，书上130-131页
            alpha2_new = self._compare(alpha2_new_unc, L, H)

            alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (
                self.alpha[i2] - alpha2_new)

            b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (
                alpha1_new - self.alpha[i1]) - self.Y[i2] * self.kernel(
                    self.X[i2],
                    self.X[i1]) * (alpha2_new - self.alpha[i2]) + self.b
            b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (
                alpha1_new - self.alpha[i1]) - self.Y[i2] * self.kernel(
                    self.X[i2],
                    self.X[i2]) * (alpha2_new - self.alpha[i2]) + self.b

            if 0 < alpha1_new < self.C:
                b_new = b1_new
            elif 0 < alpha2_new < self.C:
                b_new = b2_new
            else:
                # 选择中点
                b_new = (b1_new + b2_new) / 2

            # 更新参数
            self.alpha[i1] = alpha1_new
            self.alpha[i2] = alpha2_new
            self.b = b_new

            self.E[i1] = self._E(i1)
            self.E[i2] = self._E(i2)
        return 'train done!'

    def predict(self, data):
        r = self.b
        for i in range(self.m):
            r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])

        return 1 if r > 0 else -1

    def score(self, X_test, y_test):
        right_count = 0
        for i in range(len(X_test)):
            result = self.predict(X_test[i])
            if result == y_test[i]:
                right_count += 1
        return right_count / len(X_test)

    def _weight(self):
        # linear model
        yx = self.Y.reshape(-1, 1) * self.X
        self.w = np.dot(yx.T, self.alpha)
        return self.w

5.训练并测试参数

svm = SVM(max_iter=1000)
svm.fit(X_train, y_train)
svm.score(X_test, y_test)

以上数据及源代码请点击这里

参考：

• 统计学习方法
• medium-svm
• towards-data-science-svm
• youtube-svm