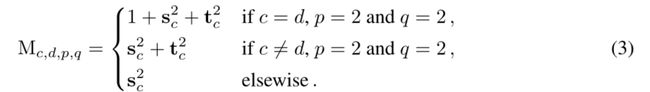RepOptimizer学习笔记

RepOptimizer学习笔记

Re-parameterizing Y our Optimizers rather than Architectures

Abstract

神经网络中设计良好的结构反映了纳入模型的先验知识。然而，虽然不同的模型具有不同的先验，但我们习惯于使用模型无关优化器（例如SGD）对其进行训练。在本文中，我们提出了一种新的范式，将特定于模型的先验知识合并到优化器中，并使用它们来训练通用（简单）模型。作为实现，我们提出了一种新的方法，通过根据一组特定于模型的超参数修改梯度来添加先验知识，称为梯度重新参数化，优化器称为重新优化器。为了模型结构的极端简单性，我们重点关注VGG风格的平面模型，并展示了这样一个使用重新优化器训练的简单模型，即RepOpt-VGG，其性能与最近设计良好的模型相当。从实用角度来看，RepOpt-VGG由于其结构简单、推理速度快和训练效率高，是一种很好的基础模型。与结构重参数化相比，结构重参数化通过构造额外的训练时间结构向模型中添加先验知识，再优化不需要额外的正向/反向计算，并解决了量化问题。代码和模型可在https://github.com/DingXiaoH/RepOptimizers.

1 Introduction

神经网络的结构设计是将先验知识纳入模型中。例如，将特征变换建模为残差加法（y=x+f（x））优于普通形式（y=f（x））[22]。ResNet将此类先验知识纳入具有快捷结构的模型，并优于没有此类先验的简单模型，例如VGGNet[42]。模型结构的最新进展表明，高质量的结构先验对神经网络至关重要。例如，EfficientNet[44]通过网络架构搜索和复合缩放获得了一组结构超参数，作为构建模型的先验知识；RegNet[36]通过改变结构超参数、生成模型和观察模式获得了丰富的先验知识。当然，更好的结构先验会导致更高的性能。

另一方面，优化方法也发挥着重要作用，可分为三类[43]。1） 一阶方法，例如SGD[38]及其变体[27、16、33]已用于各种模型，包括ConvNet[29、42、22]、LSTM[23]、Transformer[47、15]和MLP[45、46]。2） 高阶方法[40、25、35]利用曲率信息，但面临计算或近似海森矩阵[8、39]的挑战。3） 对于目标函数的导数可能不存在的情况，无导数方法[37，1]很有用。

我们注意到1）虽然高级优化器以不同的方式改进了训练过程，但它们没有特定于被优化模型的先验知识；2） 虽然我们通过设计高级结构不断将我们的最新理解融入到模型中，但我们使用SGD[38]和AdamW[33]等模型无关优化器对其进行训练，也就是说，我们长期以来一直使用特定结构+通用优化器。为了探索另一种方法，我们做出以下贡献。

A new paradigm

我们提出了通用结构+特定优化器。一般结构意味着模型应尽可能少地具有结构先验知识。特定优化器是指优化器通过以特定于模型的方式更改训练动态来实现更好的性能。

A methodology for SGD-based optimizer

本文主要研究深度神经网络等大规模非凸模型，因此我们只考虑基于SGD的优化器，但高层思想可以推广到高阶或无导数方法。由于SGD的核心是用梯度更新参数，我们建议在更新可训练参数之前，根据一组模型特定的超参数修改梯度，使优化器模型特定。我们将这种方法称为梯度重新参数化（GR），将优化器称为重新优化。为了获得这样的超参数，我们提出了一种称为超搜索的方法。

A favorable base model.

为了证明通用结构+特定优化器的有效性，我们需要一个尽可能简单的模型。当然，我们选择VGG风格的[42]架构，它只包含一个3×3 conv层的堆栈。长期以来，这种架构一直被认为不如设计良好的模型，如RegNet[36]和EfficientNet[44]，因为后者具有更丰富的结构先验。令人印象深刻的是，使用重新优化器训练的VGG类型模型，即RepOpt-VGG，可以与精心设计的模型表现相当（表3）。

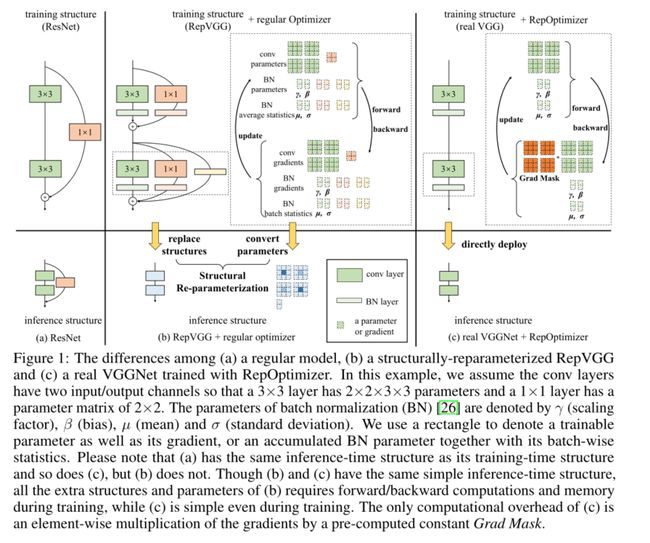
从理论方面来说，我们希望通过与RepVGG[13]及其关键方法——结构重参数化（Structural Re-parameterization）[13、12、10、9、11、14、17、52、53、48、54]（SR）的比较来强调我们工作的新颖性，该方法通过额外的训练时间结构来改变训练动态，从而提高模型的性能。我们采用RepVGG作为基线，因为它也可以生成强大的VGG风格的模型，但方法不同。具体来说，针对VGG风格的推理时间架构（称为目标结构），RepVGG构建额外的训练时间结构，然后通过SR将其转换为目标结构进行部署。差异总结如下，如图1所示。1）与常规模型（如ResNet）类似，RepVGG也将先验添加到具有良好设计结构的模型中，并利用通用优化器，但RepOpt-VGG将先验添加到优化器中。2） 与RepOpt-VGG相比，虽然转换后的RepVGG具有相同的推理时间结构，但训练时间RepVGG要复杂得多，需要消耗更多的时间和内存。换句话说，RepOpt VGG是训练期间真正的普通模型，但RepVGG不是。3） 我们扩展和深化了随机共振，表明对于随机共振的特殊情况，训练时间结构设计足够简单（每个分支仅包含一个线性可训练算子），我们可以使用自定义优化器实现等效的训练动态。这种等价性意味着SR模型（具有额外结构）和GR模型（没有额外结构，但使用修改的梯度进行更新）在训练过程中的任何迭代中产生数学上相同的输出，前提是它们具有相同的输入和训练配置。我们必须强调的是，本文设计了遵循RepVGG的重优化器的行为只是为了公平比较，其他设计也可能很好或更好；从更广泛的角度来看，我们仅展示了VGG模型+基于SGD的重优化器，但该范式可能推广到其他模型和优化方法。

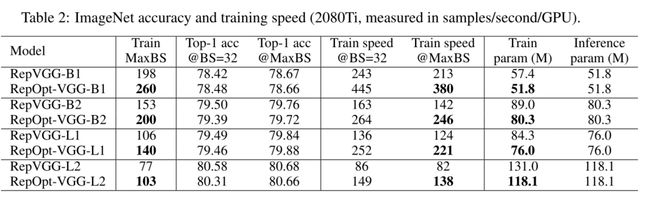
从实用角度来看，RepOpt VGG也是一种良好的基础模型，它具有高效推理和高效训练的特点。1） 作为一种极为简单的架构，它具有低内存消耗（因为它没有分支）、高并行度（一个大运算符比具有相同浮点运算的几个小运算符更高效[34]），并大大受益于高度优化的3×3 conv（例如，Winograd算法[30]）[13]。更好的是，由于模型主体仅包含一种类型的操作员，我们可以将大量3×3 conv单元集成到定制芯片上，以获得更高的效率[13]。2） 有效的培训对于计算资源有限或我们希望快速交付或快速迭代模型的应用场景，例如，我们可能需要每隔几天使用新收集的数据重新训练模型。表2显示，RepOpt-VGG的训练速度约为RepVGG的1.7倍。与推理类似，与使用通用设备（如GPU）训练的复杂模型相比，使用定制的高通量训练芯片可以更有效地训练此类简单模型。3） 除了训练效率外，重新优化器还克服了结构重新参数化[13]的一个主要缺点：量化问题。推理时间RepVGG难以通过训练后量化（PTQ）进行量化。例如，使用简单的INT8 PTQ，ImageNet[7]上RepVGG的精度降低到54.55%。在第4.4节中，我们证明了RepOpt-VGG有利于量化，并揭示了量化RepVGG的问题是由训练模型的结构转换引起的。我们很自然地用重新优化器解决了这个问题，因为重新定位VGG根本不经历结构转换。

2 Related Work

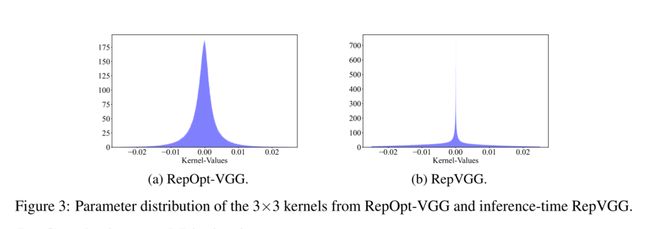
RepVGG采用了一种名为结构重参数化（SR）[13、12、10、9、11、14、17、52、53、48、54]的方法，该方法通过转换参数来转换结构。针对VGG式推理时间架构，它构造了一些额外的快捷方式（即身份映射和1×1 conv层）用于训练，并将整个块转换为单个3×3 conv。简而言之，BN层融合到前面的conv层中（注意，身份映射也可以被视为1×1 conv层，其核心是身份矩阵），将1×1 conv核添加到3×3核的中心点上（图1 b）。SR的一个显著缺点是，无法节省一般SR的额外训练成本。与REPORT VGG相比，RepVGG具有相同的目标结构，但训练结构复杂且耗时。此外，量化RepVGG可能会导致显著退化，而量化REOPT VGG与量化常规模型一样容易（第4.4节）。

GR扩展和深化了SR，就像SR扩展了再参数化的经典意义一样。作为一种典型的“重新参数化”，例如，DiracNet[50]以不同的形式对conv内核进行编码，以便于优化。具体来说，将3×3 conv核（视为矩阵）重新参数化为$\hat{W}=diag（a）I+diag（b）W_{norm}$，其中a、b是学习向量，$W_{norm}$是归一化可训练核。对于每个正向计算，conv层首先归一化其核，用a、b和$W_{norm}$计算$\hat{W}$，然后使用所得核进行卷积。然后，优化器必须导出所有参数的梯度并更新它们。与DiracNet相比，REPORT VGG不改变可训练参数的形式，也不引入额外的正向/反向计算。

3 RepOptimizers

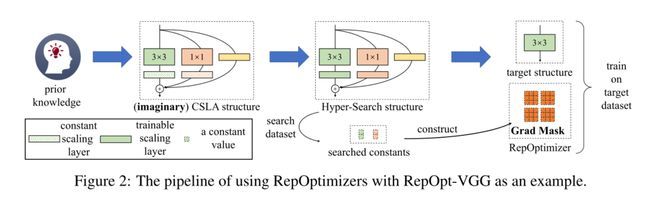
重新优化器通过更改原始训练动态来工作，但似乎很难想象如何更改训练动态以改进给定模型。为了设计和描述重优化器的行为，我们采用了三步流水线：1）定义先验知识并想象一个复杂的结构来反映知识；2） 我们研究了如何使用更简单的目标结构实现等效训练动力学，该目标结构的梯度根据一些超参数进行修改；3） 我们获得了超参数来建立重新优化。请注意，重优化器的设计取决于给定的模型和先验知识。在下面，我们使用RepOpt VGG作为展示。

3.1 Incorporate Knowledge into Structure

重新优化程序的核心是我们希望纳入优化器的先验知识。在REPORT VGG的情况下，我们知道，可以通过将多个分支的输入和输出相加来提高模型的性能，这些分支按不同的比例加权。如此简单的知识引发了多种结构设计。例如，ResNet[22]可以被视为此类知识的简单但成功的应用，它简单地组合（相加）剩余块的输入和输出；RepVGG[13]有着相似的想法，但使用了不同的实现。有了这些知识，我们设计结构来满足我们的需求。在这种情况下，我们希望改进VGG样式的模型，因此我们选择了RepVGG的结构设计（3×3 conv+1×1 conv+身份映射）。

3.2 Shift the Structural Priors into an Equivalent RepOptimizer

然后，我们描述了如何将结构先验转换为重新优化。关于上述先验知识，我们注意到一个有趣的现象：在一个特殊情况下，每个分支仅包含一个具有可选恒定尺度的线性可训练算子，只要适当设置恒定尺度值，模型的性能仍然会提高。我们将这种线性块称为恒定比例线性加法（CSLA）。

此外，我们注意到，我们可以用单个算子替换CSLA块，并通过将梯度乘以从常数尺度导出的一些常数掩码来实现等效的训练动力学（这意味着，如果使用相同的训练数据，则在任何次数的训练迭代后，它们总是产生相同的输出）。我们将此类掩码称为Grad Masks（Grad Masks）（图1）。用梯度掩模修改梯度可以被视为GR的具体实现，

我们在附录A中给出了这种等价性的证明，称为CSLA=GR。为了简单起见，这里我们只展示了两个卷积和两个常数标量作为4个标度因子的结论。假设${\alpha }_A，{\alpha }_B$是两个常数标量，$W^{（A）}，W^{（B）}$是两个形状相同的conv核，X和Y是输入和输出，∗ 表示卷积，CSLA块的计算流公式为$Y_{CSLA}={\alpha }_A（X\ast W^{（A）}）+{\alpha }_B（X\ast W^{（B）}）$。对于GR对应项，我们直接训练由$W^{{}^{\prime }}$参数化的目标结构，使$Y_{GR}=X\ast W^{{}^{\prime }}$ 假设我是训练迭代次数，我们可以确保$Y_{CSLA}^{（i）}=Y_{GR}^{（i）}{\forall }_i\ge 0$，只要我们遵循两条规则：

Rule of Initialization:$W^{{}^{\prime }}$应初始化为$W^{{}^{\prime }(0)}\leftarrow {\alpha }_A{W}^{(A)(0)}+{\alpha }_B{W}^{(B)(0)}$。换句话说**，应使用等效参数**（可通过线性轻松获得）初始化GR对应项，作为CSLA对应项，以使其初始输出相同。

Rule of Iteration:当使用常规SGD更新规则更新CSLA对应项时，GR对应项的梯度应乘以$（{\alpha }_A^2+{\alpha }_B^2）$。形式上，假设L是目标函数，λ是学习率，我们应该通过

当CSLA=GR时，我们可以通过首先设计CSLA结构来设计和描述再优化器的行为。在REPOT VGG的情况下，CSLA结构是通过简单地将RepVGG块中3×3和1×1层之后的批归一化（BN）[26]层替换为恒定的通道级缩放，将标识分支中的BN替换为可训练的通道级缩放（因为CSLA分支没有超过一个线性可训练算子）来实例化的，如图2所示。

在这种稍微复杂的情况下，卷积具有不同的核大小，然后是通道方向的常数尺度，Grad Masks将是张量，条目应分别使用相应位置上的尺度计算。我们提出了与这种CSLA块对应的梯度掩模公式，该公式将用于训练单个3×3通道。设C为通道数，s，t∈ RC分别是3×3和1×1层之后的恒定通道尺度，梯度掩模$M^{C\times C\times 3\times 3}$由以下公式构造：

直观地说，p=2和q=2意味着3×3核的中心点与1×1分支相关（就像RepVGG块将1×1 conv合并到3×3核的中心点一样）。由于可训练的通道级缩放可以被视为“深度”1×1 conv，然后是一个恒定的缩放因子1，我们在“对角线”位置向Grad Masks添加1（如果输出形状与输入形状不匹配，CSLA块将没有这样的快捷方式，因此我们只需忽略此项）。

Remark

与RepVGG等常见SR形式相比，CSLA块既没有BN等训练时间非线性，也没有序列可训练算子，还可以通过常见SR技术将其转换为产生相同推理结果的等效结构。然而，推断时间等价并不意味着训练时间等价，因为转换后的结构将具有不同的训练动态，在更新后打破了等价性。此外，我们必须强调，CSLA结构是虚构的，它只是描述和可视化再优化器的中间工具，但我们从未实际训练过它，因为结果在数学上与直接用GR训练目标结构相同。

只剩下一个问题：如何获得常数标度向量s和t？

3.3 Obtain the Hyper-Parameters of RepOptimizer via Hyper-Search

当然，作为重优化器的超参数，梯度掩模会影响性能。由于深度神经网络优化的非凸性，研究界仍然缺乏对黑箱的透彻理解，因此我们不期望得到可证明的最优解。我们提出了一种新方法，将优化器的超参数与辅助模型和搜索的可训练参数相关联，因此称为超搜索（HS）

具体来说，给定一个重优化器，我们通过用可训练的尺度替换再优化器对应的CSLA模型中的常数来构建辅助超搜索模型，并在一个小的搜索数据集上进行训练（例如，CIFAR-100[28]）。直观地说，这一步骤受到DART[32]的启发，即可训练参数的最终值是模型预期的值。在搜索数据集上进行训练后，可训练量表的最终值被视为预期值虚拟CSLA模型中的常数值。由于CSLA=GR，CSLA模型中的预期常数正是我们构建再优化器的预期Grad Masks所需的。

3.4 Train with RepOptimizer

在超搜索之后，我们使用搜索到的常数尺度为每个算子（在RepOpt VGG的情况下，每个3×3 conv层）构建重新优化器的梯度掩码，这些梯度掩码存储在内存中。在目标数据集上训练目标模型的过程中，重新优化器将在每次规则向前/向后计算（迭代规则）后，将梯度掩码明智地乘以相应算子的梯度。

我们还应该遵循初始化规则。为了使用重新优化器开始训练，我们根据搜索到的超参数重新初始化模型参数。在RepOpt VGG的情况下，就像上面最简单的示例$（W^{{}^{\prime }(0)}\leftarrow {\alpha }_A{W}^{(A)(0)}+{\alpha }_B{W}^{(B)(0)}）$，我们还应该在初始化时使用相应CSLA块的等效参数初始化每个3×3内核。更准确地说，我们假设通过MSRA初始化[21]自然初始化假想CSLA块中的3×3和1×1内核，作为一种常见做法，可训练的通道级缩放层为，另一个合理的选择是使用HS模型中的训练权重初始化虚拟的可训练通道级缩放层。如果我们假设这样做，我们应该将等式4中的1更改为逐层缩放层的第c个通道的训练权重。我们观察到最终精度的差异可以忽略不计。 在这种情况下，设$W^{（s）（0）}\in R^{C\times C\times 3\times 3}and{W}^{（t）（0）}\in R^{C\times C\times 1\times 1}$是随机初始化的3×3和1×1核，等效核由给出（注意，通道尺度是初始化为单位矩阵的1×1 conv，因此我们应该在对角中心位置加1该操作，如等式3）

我们使用$W^{{}^{\prime }(0)}$初始化RepOpt VGG模型中的3×3 conv层，因此训练动力学将等效于训练用$W^{(s)(0)}and{W}^{(t)(0)}$初始化的CSLA块。如果没有这两条规则中的任何一条，等价性就会中断，因此性能会下降（表4）。

4 Experiments

5 Conclusions and Limitations

本文提出了一种将模型先验转换为优化器的新范式，并提出了一种通过梯度重参数化（GR）实现的方法。我们希望这篇论文能够在设计良好的模型结构领域之外引发进一步的研究。然而，虽然该方法经过了实证验证，但我们相信进一步的研究（例如，数学上可证明的界限）将是有用的，这可能需要对深度神经网络的黑匣子有更深入的理解。与结构再参数化（SR）相比，我们必须强调，尽管SR（CSLA）的特例可以被视为GR的数学等价实现，但更复杂和一般的SR情况（例如，分支[10,13]中存在BN层或多个序列线性可训练算子[11,12]）不能被GR取代。