深度学习的简单原理(最适合初学者)

笔者写这篇文章的初衷是帮助即将入门深度学习的亲们，笔者在这个行业混了也小有几年了，希望从几年从业者的角度给新人们发表一下自己的理解，这些理解都是从最简单的原理出发。顺便提一嘴，笔者弟弟刚刚考完研，今后他大概率也是进入这个行业，这篇文章写的东西先前是用于带他入门的，哈哈！下面咋们开始吧~

深度学习技术目前应用于生活中方方面面，比如我们常见到的网上购物、智能家居、安防、甚至一些P图软件等，如果按照技术研究领域来分可以分为三大领域：计算机视觉(CV)、自然语言处理(NLP)、推荐。虽然这个领域有这么多五花八门的应用领域与场景，以及下辖成千上万种技术门类，但是它的基本原理都是一样的，万变不不离其中。

深度学习最基本的原理其实很简单，其实早在上个世纪就已经出现了，主要是受制于之前的算力以及存储资源的限制，导致最近十年才这么火热。笔者认为目前深度学习主要有三大部件：神经网络、目标函数、优化算法。神经网络其实就是一种表达能力非常强大的函数，只不过这个函数的一些参数是未知的，需要我们去求解，函数的表达能力后面会讲；目标函数作为神经网络的优化方向，也衡量了神经网络距离最优解的距离度量；优化算法提供了求解神经网络未知参数的策略，目前神经网络的优化算法几乎都是基于梯度下降法。读到这里如果不理解，没关系，下面我会详细介绍。

一、认识神经网络

1、神经网络本质

神经网络本质就是一个数学函数

                                                                                                                                （1）

为函数的所有的未知参数（也是我们要求解的参数），所以我们可以把这些未知参数写成一种向量形式，比如对于线性函数来说：

,那么需要求解的参数为,

比如对于正弦三角函数来说：

，那么需要求解的参数为，

比如对于二次函数来说：

，那么需要求解的参数为。

神经网络与一般函数的区别：最大的区别就是神经网络的表达能力（也叫拟合能力）非常非常非常强大，它能表示非常非常非常复杂的函数或者关系。下面我们来认识函数的表达能力。

2、函数的表达能力

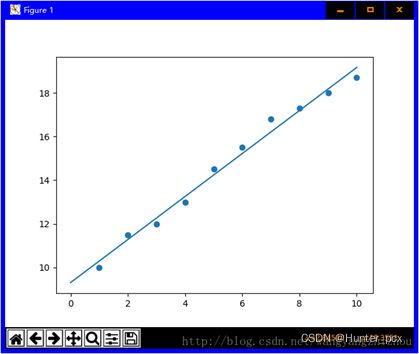
如下图所示，这些离散点的分布我们可以用一条直线很好的逼近，也就是我们可以设定一个直线方程：

 以及一个误差函数：

                                                                                                                   (2)

其中 为我们要求解的参数，为这些离散点的坐标，那么我们只需要最小化下面这个式子就可以求解出这个直线方程了：

                                                                                                      （3）

 上面这个式子可以通过求函数极值的方法求解出来，如果不了解的可以回去复习一下高数了，只不过这里需要点一下：求解（3）式的过程其实就是一个优化的过程。

    图1 线性分布逼近

那如果离散点是下面这样的分布呢？如果我们还是选择用线性函数去逼近这些点，那么势必误差会比较大；而如果选择一个二次函数去逼近这些点，那么误差就会比较小；更进一步，我们是可以用二次函数 去逼近上面图1的离散点分布，此时只要a=0，这个二次函数其实就是一个线性函数。所以二次函数可以比较好的逼近（表达）线性函数分布，线性函数却不能很好的逼近（表达）二次函数分布，因此我们说二次函数的表达能力(拟合能力)强于线性函数。因此不同的函数，表达能力(拟合能力)不同。

图2 二次函数逼近

我们之前学过的一般数学函数(比如线性函数、二次函数、正弦函数、指数函数)的表达能力都是有很大限制的，它们中的无论哪一个都不能很好地表达（逼近）一些复杂的分布（关系）。神经网络这种函数形式就比较强大了，特别是它最擅长表达复杂的逻辑运算关系。

3、神经网络的形式

神经网络有着非常强大的表达能力，但是这并不意味着我们可以设计一种通用的神经网络结构，就可以适用于所有的任务。为了能够让神经网络工作的更好(也就是有更强大的表达能力)，一般我们会利用一些先验知识（也就是经验知识）去设计神经网络结构；一般来说在不同的任务中，我们获取到的先验知识是不同的，这就导致神经网络结构也会不一样，因此很多大量的深度学习的paper也主要集中于怎么利用先验知识设计、改进神经网络的结构。

比如就拿计算机视觉(CV)中的任务与自然语言处理(NLP)中的任务来说，CV领域处理的数据类型主要是图像，传统的图像处理技术就是基于卷积运算，因为卷积运算模拟了人的视觉信号处理机制，并且能大大降低运算量，所以现在CV领域中基本上采用卷积神经网络(CNN)这样的网络结构；NLP领域一般处理的是时序数据，所以基本上采用循环神经网络(RNN)这样的网络结构。

因此对于不同的任务，神经网络的这种函数形式是不一样的。

二、目标函数

求解一个函数的未知参数，可以转化为一个最优化问题，而最优化问题需要设计一个优化函数，这个函数也叫做目标函数(它还有很多别名，比如损失函数、代价函数)。这个目标函数一般我们要最小化它(也可以最大化)，如公式(3)所示的最小化均方误差函数(MSE)。不同的任务，一般目标函数会有不一样，比如分类问题的目标函数一般为交叉熵损失函数(CE)，生成问题一般采用ganloss。

使得目标函数取得最小值(最大)的解我们叫做最优解，也就是函数（神经网络）的未知参数的解。因此设计一个比较好的目标函数是非常重要的，哪怕在同一个任务中采用不同的目标函数，那么最后求解出的神经网络效果（精度）也是有差异的。很多深度学习的paper另外一个研究方向，就是针对于设计目标函数的。

三、优化算法

 一旦我们建立好了一个最优化模型之后，那么就要用一种策略去求解出最优解，怎么求解出最优解的问题叫做最优化问题，求最优解的过程叫做最优化过程。比如我们建立好了公式(3)这样的目标函数之后，下一步我们就要用一种策略去求解出满足目标函数最小值的参数a和b，只不过这个例子比较简单，我们可以用曾经学过的函数极值的方法求解。但是对于很多复杂的情况，就不能通过这种简单的方法求最优解了。其实对于优化问题来说，专门有一门学科叫做最优化理论，比较常用的最优化算法比如拉格朗日乘子法、最小二乘法、牛顿法等，现在用的最多的是梯度下降法。

梯度下降法作为一种优化算法，其实它并不是为深度学习量身制定的，绝大部分优化问题都可以用梯度下降法去求解，只不过由于深度学习比较火热的原因，梯度下降法才广为人知。

梯度下降法特别适用于求解像神经网络这样的拥有大量未知参数的优化问题，目前几乎所有的深度学习优化算法（比如BGD、SGD、Adam、RMSprop）都是基于梯度下降法的改良，而一般业内所说的学习或者训练过程，其实就是指优化过程。

以上只代表个人的粗陋见解，如果是路过的大佬望留言讨论哈~~