机器学习十大算法案例

监督学习

1. 线性回归

梯度下降一元线性回归

import numpy as np
import matplotlib.pyplot as plt

# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0]
y_data = data[:,1]

# 学习率learning rate
lr = 0.0001
# 截距
b = 0 
# 斜率
k = 0 
# 最大迭代次数
epochs = 50

# 最小二乘法
def compute_error(b, k, x_data, y_data):
    totalError = 0
    for i in range(0, len(x_data)):
        totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
    return totalError / float(len(x_data)) / 2.0

def gradient_descent_runner(x_data, y_data, b, k, lr, epochs):
    # 计算总数据量
    m = float(len(x_data))
    # 循环epochs次
    for i in range(epochs):
        b_grad = 0
        k_grad = 0
        # 计算梯度的总和再求平均
        for j in range(0, len(x_data)):
            b_grad += (1/m) * (((k * x_data[j]) + b) - y_data[j])
            k_grad += (1/m) * x_data[j] * (((k * x_data[j]) + b) - y_data[j])
        # 更新b和k
        b = b - (lr * b_grad)
        k = k - (lr * k_grad)
    return b, k

print("Starting b = {0}, k = {1}, error = {2}".format(b, k, compute_error(b, k, x_data, y_data)))
print("Running...")
b, k = gradient_descent_runner(x_data, y_data, b, k, lr, epochs)
print("After {0} iterations b = {1}, k = {2}, error = {3}".format(epochs, b, k, compute_error(b, k, x_data, y_data)))

#画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, k*x_data + b, 'r')
plt.show()

梯度下降法-多元线性回归

import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt  
from mpl_toolkits.mplot3d import Axes3D  

# 读入数据 
data = genfromtxt(r"Delivery.csv",delimiter=',')

# 切分数据
x_data = data[:,:-1]
y_data = data[:,-1]

# 学习率learning rate
lr = 0.0001
# 参数
theta0 = 0
theta1 = 0
theta2 = 0
# 最大迭代次数
epochs = 1000

# 最小二乘法
def compute_error(theta0, theta1, theta2, x_data, y_data):
    totalError = 0
    for i in range(0, len(x_data)):
        totalError += (y_data[i] - (theta1 * x_data[i,0] + theta2*x_data[i,1] + theta0)) ** 2
    return totalError / float(len(x_data))

def gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs):
    # 计算总数据量
    m = float(len(x_data))
    # 循环epochs次
    for i in range(epochs):
        theta0_grad = 0
        theta1_grad = 0
        theta2_grad = 0
        # 计算梯度的总和再求平均
        for j in range(0, len(x_data)):
            theta0_grad += (1/m) * ((theta1 * x_data[j,0] + theta2*x_data[j,1] + theta0) - y_data[j])
            theta1_grad += (1/m) * x_data[j,0] * ((theta1 * x_data[j,0] + theta2*x_data[j,1] + theta0) - y_data[j])
            theta2_grad += (1/m) * x_data[j,1] * ((theta1 * x_data[j,0] + theta2*x_data[j,1] + theta0) - y_data[j])
        # 更新b和k
        theta0 = theta0 - (lr*theta0_grad)
        theta1 = theta1 - (lr*theta1_grad)
        theta2 = theta2 - (lr*theta2_grad)
    return theta0, theta1, theta2

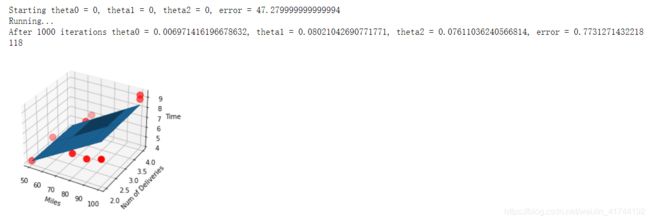
print("Starting theta0 = {0}, theta1 = {1}, theta2 = {2}, error = {3}".
      format(theta0, theta1, theta2, compute_error(theta0, theta1, theta2, x_data, y_data)))
print("Running...")
theta0, theta1, theta2 = gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs)
print("After {0} iterations theta0 = {1}, theta1 = {2}, theta2 = {3}, error = {4}".
      format(epochs, theta0, theta1, theta2, compute_error(theta0, theta1, theta2, x_data, y_data)))

ax = plt.figure().add_subplot(111, projection = '3d') 
ax.scatter(x_data[:,0], x_data[:,1], y_data, c = 'r', marker = 'o', s = 100) #点为红色三角形  
x0 = x_data[:,0]
x1 = x_data[:,1]
# 生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = theta0 + x0*theta1 + x1*theta2
# 画3D图
ax.plot_surface(x0, x1, z)
#设置坐标轴  
ax.set_xlabel('Miles')  
ax.set_ylabel('Num of Deliveries')  
ax.set_zlabel('Time')  
  
#显示图像  
plt.show()  

2. 逻辑回归

逻辑回归原理与推导
梯度下降法-逻辑回归

import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import preprocessing
# 数据是否需要标准化
scale = True

# 载入数据
data = np.genfromtxt("LR-testSet.csv", delimiter=",")
x_data = data[:,:-1]
y_data = data[:,-1]
    
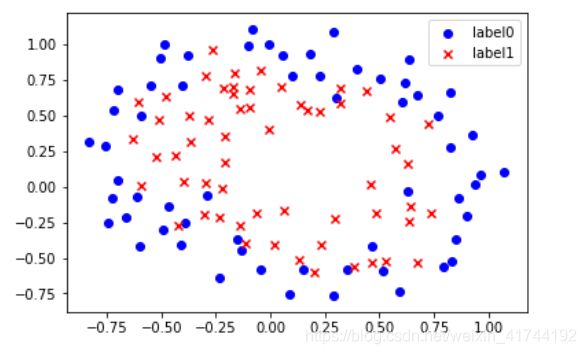
def plot():
    x0 = []
    x1 = []
    y0 = []
    y1 = []
    # 切分不同类别的数据
    for i in range(len(x_data)):
        if y_data[i]==0:
            x0.append(x_data[i,0])
            y0.append(x_data[i,1])
        else:
            x1.append(x_data[i,0])
            y1.append(x_data[i,1])

    # 画图
    scatter0 = plt.scatter(x0, y0, c='b', marker='o')
    scatter1 = plt.scatter(x1, y1, c='r', marker='x')
    #画图例
    plt.legend(handles=[scatter0,scatter1],labels=['label0','label1'],loc='best')
    
plot()
#查看数据
plt.show()

# 数据处理，添加偏置项
x_data = data[:,:-1]
y_data = data[:,-1,np.newaxis]

print(np.mat(x_data).shape)
print(np.mat(y_data).shape)
# 给样本添加偏置项
X_data = np.concatenate((np.ones((100,1)),x_data),axis=1)

def sigmoid(x):
    return 1.0/(1+np.exp(-x))

def cost(xMat, yMat, ws):
    left = np.multiply(yMat, np.log(sigmoid(xMat*ws)))
    right = np.multiply(1 - yMat, np.log(1 - sigmoid(xMat*ws)))
    return np.sum(left + right) / -(len(xMat))

def gradAscent(xArr, yArr):
    
    if scale == True:
        xArr = preprocessing.scale(xArr)
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    
    lr = 0.001
    epochs = 10000
    costList = []
    # 计算数据行列数
    # 行代表数据个数，列代表权值个数
    m,n = np.shape(xMat)
    # 初始化权值
    ws = np.mat(np.ones((n,1)))
    
    for i in range(epochs+1):             
        # xMat和weights矩阵相乘
        h = sigmoid(xMat*ws)   
        # 计算误差
        ws_grad = xMat.T*(h - yMat)/m
        ws = ws - lr*ws_grad 
        
        if i % 50 == 0:
            costList.append(cost(xMat,yMat,ws))
    return ws,costList

# 训练模型，得到权值和cost值的变化
ws,costList = gradAscent(X_data, y_data)
print(ws)

if scale == False:
    # 画图决策边界
    plot()
    x_test = [[-4],[3]]
    y_test = (-ws[0] - x_test*ws[1])/ws[2]
    plt.plot(x_test, y_test, 'k')
    plt.show()

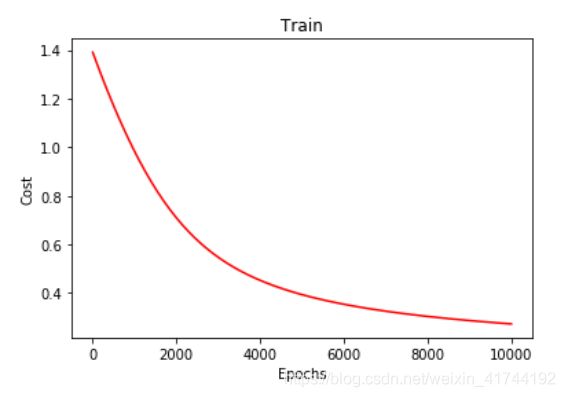
# 画图 loss值的变化
x = np.linspace(0,10000,201)
plt.plot(x, costList, c='r')
plt.title('Train')
plt.xlabel('Epochs')
plt.ylabel('Cost')
plt.show()

# 预测
def predict(x_data, ws):
    if scale == True:
        x_data = preprocessing.scale(x_data)
    xMat = np.mat(x_data)
    ws = np.mat(ws)
    return [1 if x >= 0.5 else 0 for x in sigmoid(xMat*ws)]

predictions = predict(X_data, ws)

print(classification_report(y_data, predictions))

梯度下降法-非线性逻辑回归

import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import preprocessing
from sklearn.preprocessing import PolynomialFeatures
# 数据是否需要标准化
scale = False

# 载入数据
data = np.genfromtxt("LR-testSet2.txt", delimiter=",")
x_data = data[:,:-1]
y_data = data[:,-1,np.newaxis]
    
def plot():
    x0 = []
    x1 = []
    y0 = []
    y1 = []
    # 切分不同类别的数据
    for i in range(len(x_data)):
        if y_data[i]==0:
            x0.append(x_data[i,0])
            y0.append(x_data[i,1])
        else:
            x1.append(x_data[i,0])
            y1.append(x_data[i,1])

    # 画图
    scatter0 = plt.scatter(x0, y0, c='b', marker='o')
    scatter1 = plt.scatter(x1, y1, c='r', marker='x')
    #画图例
    plt.legend(handles=[scatter0,scatter1],labels=['label0','label1'],loc='best')
    
plot()
plt.show()

# 定义多项式回归,degree的值可以调节多项式的特征
poly_reg  = PolynomialFeatures(degree=3) 
# 特征处理
x_poly = poly_reg.fit_transform(x_data)

def sigmoid(x):
    return 1.0/(1+np.exp(-x))

def cost(xMat, yMat, ws):
    left = np.multiply(yMat, np.log(sigmoid(xMat*ws)))
    right = np.multiply(1 - yMat, np.log(1 - sigmoid(xMat*ws)))
    return np.sum(left + right) / -(len(xMat))

def gradAscent(xArr, yArr):
    
    if scale == True:
        xArr = preprocessing.scale(xArr)
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    
    lr = 0.03
    epochs = 50000
    costList = []
    # 计算数据列数，有几列就有几个权值
    m,n = np.shape(xMat)
    # 初始化权值
    ws = np.mat(np.ones((n,1)))
    
    for i in range(epochs+1):             
        # xMat和weights矩阵相乘
        h = sigmoid(xMat*ws)   
        # 计算误差
        ws_grad = xMat.T*(h - yMat)/m
        ws = ws - lr*ws_grad 
        
        if i % 50 == 0:
            costList.append(cost(xMat,yMat,ws))
    return ws,costList

# 训练模型，得到权值和cost值的变化
ws,costList = gradAscent(x_poly, y_data)
print(ws)


# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1

# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))

# np.r_按row来组合array， 
# np.c_按colunm来组合array
# >>> a = np.array([1,2,3])
# >>> b = np.array([5,2,5])
# >>> np.r_[a,b]
# array([1, 2, 3, 5, 2, 5])
# >>> np.c_[a,b]
# array([[1, 5],
#        [2, 2],
#        [3, 5]])
# >>> np.c_[a,[0,0,0],b]
# array([[1, 0, 5],
#        [2, 0, 2],
#        [3, 0, 5]])
z = sigmoid(poly_reg.fit_transform(np.c_[xx.ravel(), yy.ravel()]).dot(np.array(ws)))# ravel与flatten类似，多维数据转一维。flatten不会改变原始数据，ravel会改变原始数据
for i in range(len(z)):
    if z[i] > 0.5:
        z[i] = 1
    else:
        z[i] = 0
z = z.reshape(xx.shape)

# 等高线图
cs = plt.contourf(xx, yy, z)
plot() 
plt.show()

# 预测
def predict(x_data, ws):
#     if scale == True:
#         x_data = preprocessing.scale(x_data)
    xMat = np.mat(x_data)
    ws = np.mat(ws)
    return [1 if x >= 0.5 else 0 for x in sigmoid(xMat*ws)]

predictions = predict(x_poly, ws)

print(classification_report(y_data, predictions))

3. 神经网络

神经网络

4. SVM支持向量机

SVM-非线性

import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import svm

# 载入数据
data = np.genfromtxt("LR-testSet2.txt", delimiter=",")
x_data = data[:,:-1]
y_data = data[:,-1]
    
def plot():
    x0 = []
    x1 = []
    y0 = []
    y1 = []
    # 切分不同类别的数据
    for i in range(len(x_data)):
        if y_data[i]==0:
            x0.append(x_data[i,0])
            y0.append(x_data[i,1])
        else:
            x1.append(x_data[i,0])
            y1.append(x_data[i,1])

    # 画图
    scatter0 = plt.scatter(x0, y0, c='b', marker='o')
    scatter1 = plt.scatter(x1, y1, c='r', marker='x')
    #画图例
    plt.legend(handles=[scatter0,scatter1],labels=['label0','label1'],loc='best')
    
plot()
plt.show()

# fit the model
# C和gamma
model = svm.SVC(kernel='rbf')
model.fit(x_data, y_data)

model.score(x_data,y_data)

# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1

# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))

z = model.predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似，多维数据转一维。flatten不会改变原始数据，ravel会改变原始数据
z = z.reshape(xx.shape)

# 等高线图
cs = plt.contourf(xx, yy, z)
plot() 
plt.show()

5. K邻近

主要过程


案例

# 导入算法包以及数据集
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from tqdm.notebook import tqdm
from sklearn.metrics import classification_report,confusion_matrix
import operator
import random

def knn(x_test, x_data, y_data, k):
    # 计算样本数量
    x_data_size = x_data.shape[0]
    # 复制x_test
    np.tile(x_test, (x_data_size,1))
    # 计算x_test与每一个样本的差值
    diffMat = np.tile(x_test, (x_data_size,1)) - x_data
    # 计算差值的平方
    sqDiffMat = diffMat**2
    # 求和
    sqDistances = sqDiffMat.sum(axis=1)
    # 开方
    distances = sqDistances**0.5
    # 从小到大排序
    sortedDistances = distances.argsort()
    classCount = {}
    for i in range(k):
        # 获取标签
        votelabel = y_data[sortedDistances[i]]
        # 统计标签数量
        classCount[votelabel] = classCount.get(votelabel,0) + 1
    # 根据operator.itemgetter(1)-第1个值对classCount排序，然后再取倒序
    sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1), reverse=True)
    # 获取数量最多的标签
    return sortedClassCount[0][0]

# 载入数据
iris = datasets.load_iris()

#打乱数据
data_size = iris.data.shape[0]
index = [i for i in range(data_size)] 
random.shuffle(index)  
iris.data = iris.data[index]
iris.target = iris.target[index]

#切分数据集
test_size = 40
x_train = iris.data[test_size:]
x_test =  iris.data[:test_size]
y_train = iris.target[test_size:]
y_test = iris.target[:test_size]

#分类
predictions = []
for i in tqdm(range(x_test.shape[0])):
    predictions.append(knn(x_test[i], x_train, y_train, 5))
    
#评估
target_names = ['class 0', 'class 1', 'class 2']
print(classification_report(y_test, predictions,target_names=target_names))

6. 贝叶斯

设每个数据样本用一个n维特征向量来描述n个属性的值，即：X={x1，x2，…，xn}，假定有m个类，分别用C1, C2,…，Cm表示。给定一个未知的数据样本X（即没有类标号），若朴素贝叶斯分类法将未知的样本X分配给类Ci，则一定是
P(Ci|X)>P(Cj|X) 1≤j≤m，j≠i

from sklearn.naive_bayes import  GaussianNB
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import LabelEncoder
import pandas as pd
from numpy import *
import operator
#计算高斯分布密度函数的值
def calculate_gaussian_probability(mean, var, x):
    coeff = (1.0 / (math.sqrt((2.0 * math.pi) * var)))
    exponent = math.exp(-(math.pow(x - mean, 2) / (2 * var)))
    c= coeff * exponent
    return c
#计算均值
def averagenum(num):
    nsum = 0
    for i in range(len(num)):
        nsum += num[i]
    return nsum / len(num)
#计算方差
def var(list,avg):
     var1=0
     for i in list:
       var1+=float((i-avg)**2)
     var2=(math.sqrt(var1/(len(list)*1.0)))
     return var2
#朴素贝叶斯分类模型
def Naivebeys(splitData, classset, test):
    classify = []
    for s in range(len(test)):
        c = {}
        for i in classset:
            splitdata = splitData[i]
            num = len(splitdata)
            mu = num + 2
            character = len(splitdata[0])-1    #具体数据集，个数有变
            classp = []
            for j in range(character):
                zi = 1
                if isinstance(splitdata[0][j], (int, float)):
                    numlist=[example[j] for example in splitdata]
                    Mean=averagenum(numlist)
                    Var=var(numlist,Mean)
                    a = calculate_gaussian_probability(Mean, Var, test[s][j])
                else:
                    for l in range(num):
                        if test[s][j] == splitdata[l][j]:
                            zi += 1
                    a=zi/mu
                classp.append(a)
            zhi = 1
            for k in range(character):
                zhi *= classp[k]
            c.setdefault(i, zhi)
        sorta = sorted(c.items(), key=operator.itemgetter(1), reverse=True)
        classify.append(sorta[0][0])
    return classify
#评估
def accuracy(y, y_pred):
    yarr=array(y)
    y_predarr=array(y_pred)
    yarr = yarr.reshape(yarr.shape[0], -1)
    y_predarr = y_predarr.reshape(y_predarr.shape[0], -1)
    return sum(yarr == y_predarr) / len(yarr)
#数据处理
def splitDataset(dataSet):   #按照属性把数据划分
    classList = [example[-1] for example in dataSet]
    classSet = set(classList)
    splitDir = {}
    for i in classSet:
        for j in range(len(dataSet)):
            if dataSet[j][-1] == i:
                splitDir.setdefault(i, []).append(dataSet[j])
    return splitDir, classSet
    
open('test.txt')
df = pd.read_csv('test.txt')
class_le = LabelEncoder()
dataSet = df.values[:, :]
dataset_train,dataset_test=train_test_split(dataSet, test_size=0.1)
splitDataset_train, classSet_train = splitDataset(dataset_train)
classSet_test=[example[-1] for example in dataset_test]
y_pred= Naivebeys(splitDataset_train, classSet_train, dataset_test)
accu=accuracy(classSet_test,y_pred)
print("Accuracy:", accu)

Accuracy: 0.65

7. 决策树

决策树的分类模型是树状结构，简单直观，比较符合人类的理解方式。决策树分类器的构造不需要任何领域知识和参数设置，适合于探索式知识的发现。由于决策树分类步骤简单快速，而且一般来说具有较高的准确率，因此得到了较多的使用。

信息量
某事件发生所含有的信息量是该事件发生概率的函数：其中，$p(x_i)$是$x_i$发生的概率，$I(x_i)$表示$x_i$发生所含的信息量，称为$x_i$的自信息量，单位是比特$(b)$
$$I(x_i)=-{\log }_{2}p(x_i)$$
信息熵
如果将信息源所有可能事件的自信息量进行平均，即可得到信息的“熵”。设信息源$X$的符号集为$x_i(i=1,2,\cdots ,N)$，$x_i$出现的概率为$p(x_i)$，则信息源$X$的熵为：
$$H(X)=\sum _{i=1}^{N}p(x_i)I(x_i)=-\sum _{i=1}^{N}p(x_i){\log }_{2}p(x_i)$$
ID3算法
ID3算法是Quinlan于1986年提出的，只能处理离散型描述属性，在选择根节点和各个内部节点上的分枝属性时，采用信息增益作为度量标准，选择具有最高信息增益的描述属性作为分枝属性。

假设$n_j$是数据集$X$中属于类别$c_j$的样本数量，则各类别的先验概率为$p(c_j)=\frac{n_j}{total}，j=1,2,\cdots ,m$。

数据集$X$的期望信息为：
$$I(n_1,n_2,\cdots ,n_m)=-\sum _{i=1}^{N}p(c_j){\log }_{2}p(c_j)$$

由描述属性$A_f$划分数据集$X$所得的熵为：
$$E(A_f)=\sum _{s=1}^q\frac{n_{1s}+\cdots +n_{ms}}{total}I(n_{1s},\cdots ,n_{ms})$$

其中：
$$I(n_{1s},\cdots ,n_{ms})=-\sum _{j=1}^m{p}_{js}{\log }_2{p}_{js}$$
$$p_{js}=\frac{n_{js}}{n_s}$$

Af划分数据集产生的信息增益为：
$$Gain(A_f)=I(n_1,n_2,\cdots ,n_m)-E(A_f)$$

数据集介绍
本实验采用西瓜数据集，根据西瓜的几种属性判断西瓜是否是好瓜。数据集包含17条记录，数据格式如下：

色泽	根蒂	敲声	纹理	脐部	触感	好瓜
青绿	蜷缩	浊响	清晰	凹陷	硬滑	是
乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	是
乌黑	蜷缩	浊响	清晰	凹陷	硬滑	是
$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$

实验
首先我们引入必要的库：

import pandas as pd
from math import log2
from pylab import *
import matplotlib.pyplot as plt

导入数据
读取csv文件中的数据记录并转为列表

def load_dataset():
    # 数据集文件所在位置
    path = "./西瓜.csv"
    data = pd.read_csv(path, header=0)
    dataset = []
    for a in data.values:
        dataset.append(list(a))
    # 返回数据列表
    attribute = list(data.keys())
    # 返回数据集和每个维度的名称
    return dataset, attribute
dataset,attribute = load_dataset()
attribute,dataset

(['色泽', '根蒂', '敲声', '纹理', '脐部', '触感', '好瓜'],
 [['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '是'],
  ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '是'],
  ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '是'],
  ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '是'],
  ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '是'],
  ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '是'],
  ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '是'],
  ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '是'],
  ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '否'],
  ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '否'],
  ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '否'],
  ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '否'],
  ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '否'],
  ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '否'],
  ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '否'],
  ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', '否'],
  ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '否']])

计算信息熵

def calculate_info_entropy(dataset):
    # 记录样本数量
    n = len(dataset)
    # 记录分类属性数量
    attribute_count = {}
    # 遍历所有实例，统计类别出现频次
    for attribute in dataset:
        # 每一个实例最后一列为类别属性，因此取最后一列
        class_attribute = attribute[-1]
        # 如果当前类标号不在label_count中，则加入该类标号
        if class_attribute not in attribute_count.keys():
            attribute_count[class_attribute] = 0
        # 类标号出现次数加1
        attribute_count[class_attribute] += 1
    info_entropy = 0
    for class_attribute in attribute_count:
        # 计算该类在实例中出现的概率
        p = float(attribute_count[class_attribute]) / n
        info_entropy -= p * log2(p)
    return info_entropy

数据集划分

def split_dataset(dataset,i,value):
    split_set = []
    for attribute in dataset:
        if attribute[i] == value:
            # 删除该维属性
            reduce_attribute = attribute[:i]
            reduce_attribute.extend(attribute[i+1:])
            split_set.append(reduce_attribute)
    return split_set

计算属性划分数据集的熵

def calculate_attribute_entropy(dataset,i,values):
    attribute_entropy = 0
    for value in values:
        sub_dataset = split_dataset(dataset,i,value)
        p = len(sub_dataset) / float(len(dataset))
        attribute_entropy += p*calculate_info_entropy(sub_dataset)
    return attribute_entropy

计算信息增益

def calculate_info_gain(dataset,info_entropy,i):
    # 第i维特征列表
    attribute = [example[i] for example in dataset]
    # 转为不重复元素的集合
    values = set(attribute)
    attribute_entropy = calculate_attribute_entropy(dataset,i,values)
    info_gain = info_entropy - attribute_entropy
    return info_gain

根据信息增益进行划分

def split_by_info_gain(dataset):
    # 描述属性数量
    attribute_num = len(dataset[0]) - 1
    # 整个数据集的信息熵
    info_entropy = calculate_info_entropy(dataset)
    # 最高的信息增益
    max_info_gain = 0
    # 最佳划分维度属性
    best_attribute = -1
    for i in range(attribute_num):
        info_gain = calculate_info_gain(dataset,info_entropy,i)
        if(info_gain > max_info_gain):
            max_info_gain = info_gain
            best_attribute = i
    return best_attribute

构造决策树

def create_tree(dataset,attribute):
    # 类别列表
    class_list = [example[-1] for example in dataset]
    # 统计类别class_list[0]的数量
    if class_list.count(class_list[0]) == len(class_list):
        # 当类别相同则停止划分
        return class_list[0]
    # 最佳划分维度对应的索引
    best_attribute = split_by_info_gain(dataset)
    # 最佳划分维度对应的名称
    best_attribute_name = attribute[best_attribute]
    tree = {best_attribute_name:{}}
    del(attribute[best_attribute])
    # 查找需要分类的特征子集
    attribute_values = [example[best_attribute] for example in dataset]
    values = set(attribute_values)
    for value in values:
        sub_attribute = attribute[:]
        tree[best_attribute_name][value] =create_tree(split_dataset(dataset,best_attribute,value),sub_attribute)
    return tree
tree = create_tree(dataset,attribute)
tree

{'纹理': {'清晰': {'根蒂': {'蜷缩': '是',
    '硬挺': '否',
    '稍蜷': {'色泽': {'青绿': '是', '乌黑': {'触感': {'软粘': '否', '硬滑': '是'}}}}}},
  '模糊': '否',
  '稍糊': {'触感': {'软粘': '是', '硬滑': '否'}}}}

# 定义划分属性节点样式
attribute_node = dict(boxstyle="round", color='#00B0F0')
# 定义分类属性节点样式
class_node = dict(boxstyle="circle", color='#00F064')
# 定义箭头样式
arrow = dict(arrowstyle="<-", color='#000000')

# 计算叶结点数
def get_num_leaf(tree):
    numLeafs = 0
    firstStr = list(tree.keys())[0]
    secondDict = tree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += get_num_leaf(secondDict[key])
        else:
            numLeafs += 1
    return numLeafs

# 计算树的层数
def get_depth_tree(tree):
    maxDepth = 0
    firstStr = list(tree.keys())[0]
    secondDict = tree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            thisDepth = 1 + get_depth_tree(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth:
            maxDepth = thisDepth
    return maxDepth

# 绘制文本框
def plot_text(cntrPt, parentPt, txtString):
    xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
    yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)

绘制树结构

def plotTree(tree, parentPt, nodeTxt):
    numLeafs = get_num_leaf(tree)
    depth = get_depth_tree(tree)
    firstStr = list(tree.keys())[0]
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)
    plot_text(cntrPt, parentPt, nodeTxt)  #在父子结点间绘制文本框并填充文本信息
    plotNode(firstStr, cntrPt, parentPt, attribute_node)  #绘制带箭头的注释
    secondDict = tree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, class_node)
            plot_text((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD

# 绘制箭头
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
                            xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow)

# 绘图
def createPlot(tree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    plotTree.totalW = float(get_num_leaf(tree))
    plotTree.totalD = float(get_depth_tree(tree))
    plotTree.xOff = -0.5 / plotTree.totalW;
    plotTree.yOff = 1.0;
    plotTree(tree, (0.5, 1.0), '')
    plt.show()

#指定默认字体
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
# 绘制决策树
createPlot(tree)

8. 集成学习(Adaboost)

集成学习（Ensemble Learning），就是使用一系列学习器进行学习，并使用某种规则将各个学习器的结果进行整合，从而获得比单个学习器效果更好的学习效果的一种方法。

集成学习的条件
通过集成学习提高分类器的整体泛化能力有以下两个条件：

1. 基分类器之间具有差异性。如果使用的是同一个分类器集成，集成分类器的性能是不会有提升的。
2. 每个基分类器的分类精度必须大于0.5。如下图所示，当基分类器精度小于0.5时，随着集成规模的增加，分类集成分类器的分类精度会下降；但是如果基分类器的精度大于0.5时，集成分类器的最终分类精度是趋近于1的。

集成学习的两个关键点：

1. 如何构建具有差异性的基分类器
2. 如何对基分类器的结果进行整合

构建差异性分类器一般有以下三种方法：

1. 通过处理数据集生成差异性分类器
2. 通过处理数据特征构建差异性分类器
3. 对分类器的处理构建差异性分类器

集成学习常见的三种元算法是Bagging, Boosting和Stacking。Bagging用于提升机器学习算法的稳定性和准确性。Boosting主要用于减少bias（偏差）和variance（方差），是将一个弱分类器转化为强分类器的算法。Stacking是一种组合多个模型的方法。


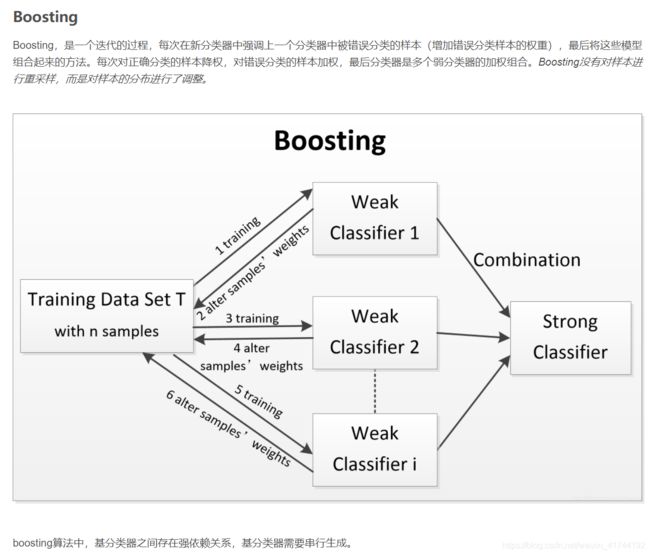
Boosting与AdaBoost算法的训练

Boosting分类方法，其过程如下所示：

1）先通过对N个训练数据的学习得到第一个弱分类器h1；

2）将h1分错的数据和其他的新数据一起构成一个新的有N个训练数据的样本，通过对这个样本的学习得到第二个弱分类器h2；

3）将h1和h2都分错了的数据加上其他的新数据构成另一个新的有N个训练数据的样本，通过对这个样本的学习得到第三个弱分类器h3；

4）最终经过提升的强分类器h_final=Majority Vote(h1,h2,h3)。即某个数据被分为哪一类要通过h1,h2,h3的多数表决。

上述Boosting算法，存在两个问题：

①如何调整训练集，使得在训练集上训练弱分类器得以进行。

②如何将训练得到的各个弱分类器联合起来形成强分类器。

针对以上两个问题，AdaBoost算法进行了调整：

①使用加权后选取的训练数据代替随机选取的训练数据，这样将训练的焦点集中在比较难分的训练数据上。

②将弱分类器联合起来时，使用加权的投票机制代替平均投票机制。让分类效果好的弱分类器具有较大的权重，而分类效果差的分类器具有较小的权重。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_gaussian_quantiles
from sklearn.metrics import classification_report

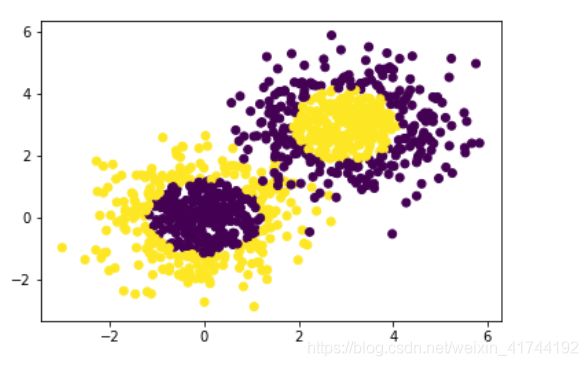
# 生成2维正态分布，生成的数据按分位数分为两类，500个样本,2个样本特征
x1, y1 = make_gaussian_quantiles(n_samples=500, n_features=2,n_classes=2)
# 生成2维正态分布，生成的数据按分位数分为两类，400个样本,2个样本特征均值都为3
x2, y2 = make_gaussian_quantiles(mean=(3, 3), n_samples=500, n_features=2, n_classes=2)
# 将两组数据合成一组数据
x_data = np.concatenate((x1, x2))
y_data = np.concatenate((y1, - y2 + 1))

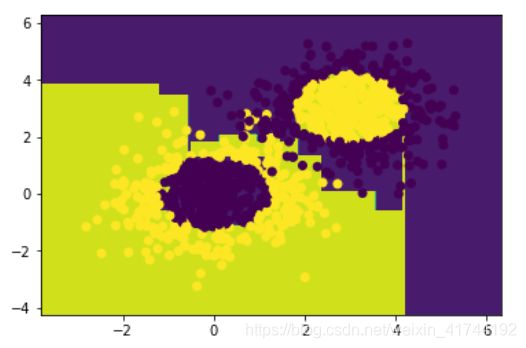
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()

# 决策树模型
model = tree.DecisionTreeClassifier(max_depth=3)

# 输入数据建立模型
model.fit(x_data, y_data)

# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1

# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))

z = model.predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似，多维数据转一维。flatten不会改变原始数据，ravel会改变原始数据
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()

# 模型准确率
model.score(x_data,y_data)

0.777

# AdaBoost模型
model = AdaBoostClassifier(DecisionTreeClassifier(max_depth=3),n_estimators=10)
# 训练模型
model.fit(x_data, y_data)

# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1

# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))

# 获取预测值
z = model.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()

# 模型准确率
model.score(x_data,y_data)

0.976

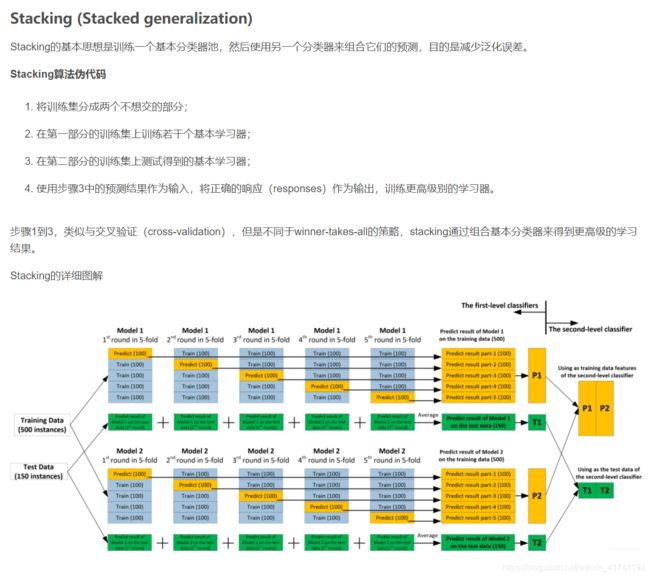
总结一下，组合算法（combiner algorithm）使用所有其他算法的预测作为附加输入（additional inputs）来训练得到最终的预测结果。理论上可以表示任何一种组合学习方法（ensemble techniques）；实际中，单层的逻辑回归模型（single-layer logistic regression model）通常被用作组合器（combiner）。

非监督学习

9. 降维—主成分分析

import numpy as np
import matplotlib.pyplot as plt

# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)
plt.show()
print(x_data.shape)

# 数据中心化
def zeroMean(dataMat):
    # 按列求平均，即各个特征的平均
    meanVal = np.mean(dataMat, axis=0) 
    newData = dataMat - meanVal
    return newData, meanVal

newData,meanVal=zeroMean(data)  
# np.cov用于求协方差矩阵，参数rowvar=0说明数据一行代表一个样本
covMat = np.cov(newData, rowvar=0)

# 协方差矩阵
covMat

array([[ 94.99190951, 125.62024804],
       [125.62024804, 277.49520751]])

# np.linalg.eig求矩阵的特征值和特征向量
eigVals, eigVects = np.linalg.eig(np.mat(covMat))

# 特征值
eigVals

array([ 30.97826888, 341.50884814])

# 特征向量
eigVects

matrix([[-0.89098665, -0.45402951],
        [ 0.45402951, -0.89098665]])

# 对特征值从小到大排序
eigValIndice = np.argsort(eigVals)
eigValIndice

array([0, 1], dtype=int64)

top = 1
# 最大的n个特征值的下标
n_eigValIndice = eigValIndice[-1:-(top+1):-1]

n_eigValIndice

array([1], dtype=int64)

# 最大的n个特征值对应的特征向量
n_eigVect = eigVects[:,n_eigValIndice]
n_eigVect

matrix([[-0.45402951],
        [-0.89098665]])

# 低维特征空间的数据
lowDDataMat = newData*n_eigVect
lowDDataMat

# 利用低纬度数据来重构数据
reconMat = (lowDDataMat*n_eigVect.T) + meanVal
reconMat

# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)

# 重构的数据
x_data = np.array(reconMat)[:,0]
y_data = np.array(reconMat)[:,1]
plt.scatter(x_data,y_data,c='r')
plt.show()

10. 聚类分析

跳转 —>聚类分析综述与案例实现