【转载】VoxelMorph 论文笔记

转载自：【论文笔记】VoxelMorph-无监督医学图像配准模型

本文是无监督的医学图像配准模型——VoxelMorph 的论文笔记。

变形配准（Deformable registration）策略通常包括两步：第一步是可实现全局对齐的仿射变形，然后是具有自由度更高的更缓慢变形变换。本文主要是关心第二步。

一、记号

$f$ 和 $m$ 分别表示 fixed image 和 moving image，$\varphi$ 表示从 $f$ 的坐标映射到 $m$ 的坐标的配准场，$u$ 表示一个位移向量场。$g_{\theta }(f,m)=u$ 是 VoxelMorph 所表示的配准函数，其中 $\theta$ 是网络的模型，$u$ 是位移场。对与体素 $p$ 来说，$u(p)$ 就是让 $m$ 中的体素和 $f$ 中的体素对齐到相似位置的位移。

二、前人工作

基于学习就是指经过神经网络训练的(训练就是学习)，训练出来的参数函数是共享的（只需训练一次得到参数，以后配准都使用这些参数）；不基于学习是指传统的配准方法，每次配准都要对度量函数进行优化，参数不共享。

由于传统的配准方法是对每一个图像对进行优化，所以速度非常慢。有监督的神经网络训练的方式虽然提升了速度，但需要大量的标注信息。无监督的神经网络训练具有速度快、不需要标注信息的特点。

这一部分是自己总结的，论文中没有。

三、VoxelMorph 网络结构

上图是 VoxelMorph 网络的示意图，下方浅蓝色区域是可选的。fixed image 和 moving image 通过一个卷积神经网络 $g_{\theta }(f,m)$ 产生一个配准场（可以理解为形变场）$\varphi$，然后将该形变场作用在 moving image 上得到更接近 fixed image 的 moved image $m\circ \varphi$。形变场有一个平滑损失 $L_{smooth}(\varphi )$，moved image 和 fixed image 之间有一个相似性损失 $L_{sim}(f,m\circ \varphi )$。如果是有监督（即有分割标签）的训练，则产生的形变场还会作用在 moving image 对应的分割标签上，得到 moved segmentation，并计算它与 fixed image segmentation 之间的分割损失 $L_{seg}(s_f,s_m\circ \varphi )$。

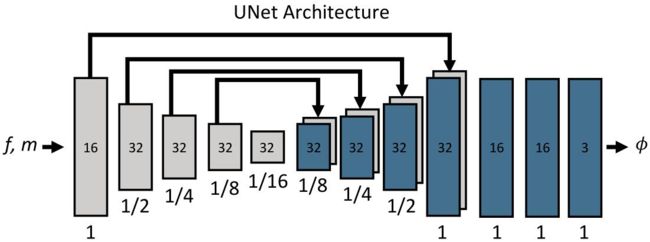
上图是本论文中使用的用来实现 $g_{\theta }(f,m)$ 的 U-Net 结构的 CNN 示意图，矩形下方的数字表示当前层三维图像的体积与输入的三维图像的关系。

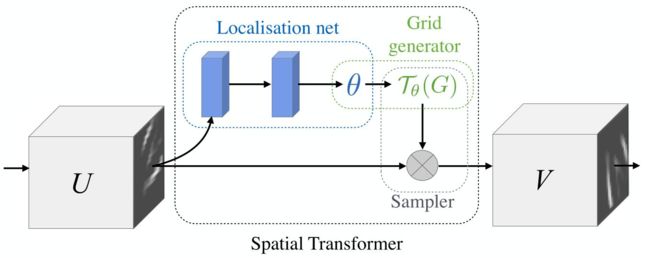
四、空间变换函数 STN

如图所示，STN 由三个顺序组件组成：

• 首先，定位网络 location net 具有非常灵活的结构，例如可以放入常规 MLP 甚至迷你 CNN，它基于作为损失函数的预定义相似性度量，学习输入的特征图的变换参数。
• 第二，网格生成器 grid generater，其目的是将定位网络预测的变换参数应用于输入的特征图。
• 最后，一个采样器 sampler 作为插值器来构造最终输出的扭曲图像。

由于 STN 是完全可微的，它可以插入网络中的任何位置，其位置是特定于上下文的，这是社区中分歧的来源。STN 不是无缺陷的；较大的变形可能会导致输出严重失真，因为采样器无法容忍这种情况，而边界插值对于采样器来说也非常困难，因为一些输出应该来自输入的外部，而那些并不存在。

简单来说，基于空间变换网络（STN）来缩小 moving image 和 fixed image 之间的区别，就是通过网格生成器 grid generater 预测一个形变场，通过采样器 sampler 将形变场作用（插值）到 moving image 上得到与 fixed image 更相似的 moved image，即 $m\circ \varphi$。

五、损失函数

VoxelMorph 中有两种训练策略或者说损失函数，一种是基于图像的灰度值来最大化一个关于图像之间的匹配程度的目标函数，另一种除此之外还使用了诸如图像的分割标签等辅助信息。显然，第一种策略是无监督的，第二种是有监督的。

1. 无监督的损失函数

无监督的损失函数包括两部分：相似性损失 $L_{sim}$ 和平滑损失 $L_{smooth}$ ，相似性损失是衡量图像之间相似性的，而平滑损失是使产生的形变具有空间平滑性的。无监督损失函数可以表示为：
$$L_{us}(f,m,\varphi )=L_{sim}(f,m\circ \varphi )+\lambda L_{smooth}(\varphi )$$
相似性损失可以是像素级的 均方误差，通常当 $f$ 和 $m$ 具有相似的灰度值分布的时候使用这种形式；也可以是 $f$ 和 $m\circ \varphi$ 之间局部的 互相关，通常当 $f$ 和 $m$ 来自不同的扫描设备或数据集时使用这种形式。

2. 有监督的损失函数

有监督的损失函数包括两部分：一部分是无监督损失，另一部分是两幅图像的分割标签之间的 Dice 损失。有监督的损失函数可以表示为：
$$L_a(f,m,s_f,s_m,\varphi )=L_{us}(f,m,\varphi )+\gamma L_{seg}(s_f,s_m\circ \varphi )$$
其中 $s_f,s_m$ 分别为 fixed image 和 moving image 对应的分割标签，需要注意的是分割损失只在训练的时候使用，在测试的时候因为没有标签所以不用。

对于分割损失来说，产生的形变场也会作用在 moving image 的分割标签上，得到 moved image 对应的分割标签，然后计算它与 fixed image 的分割标签之间的 Dice 损失。

实践证明，在使用了额外的分割信息之后，训练的效果得到了提升。

六、实验

所有的实验都是在3D图像上做的，但是为了方便表示，示意图中画的都是2D的。

1. 实验配置

实验选用了有3731张T1权重的脑部MRI的数据集，包括OASIS、ABIDE、ADHD200 、MCIC、PPMI、HABS、Harvard GSP和the FreeSurfer Buckner40数据集。在预处理阶段先将图像重采样为$256\times 256\times 256$大小，进行仿射空间正则化，并使用FreeSurfer工具提取脑部（去除头骨）并获取分割结果，再将结果图裁剪到$160\times 192\times 224$大小。训练集、验证集和测试集包含的图像数分别为3231、250和250。评价指标选用的是DICE值，它可以衡量图像的重叠情况。并使用Jacobian矩阵$J_{\varphi }(\mathbf{p})=\nabla \varphi (\mathbf{p})\in {\mathcal{R}}^{3\times 3}$来捕获体素$p$附近形变场$\varphi$的局部属性，计算所有满足$|J_{\varphi }(p)|\le 0$的非背景体素，其中变形不是微分同胚的。使用ANTs软件包里的SyN配准算法和NiftyReg作为两个baselilne，VoxelMorph的设置为：选用学习率为$1e^{-4}$的ADAM优化器，迭代1.5w次。

2. 实验一

实验一做了基于图谱的（atlas-based）配准实验，使用不同的正则化参数$\lambda$训练网络。图谱表示一个参考图像或平均图像，通常是通过联合和反复校准MRI图像数据集并将它们平均在一起来构建的。它和fixed image的作用相同，但是fixed image只是一张图片，而atlas是图像数据集的平均。

上表展示了采用不同模型的平均DICE值和运行时间，VoxelMorph的DICE值差不多可以和ANTs以及NiftyReg相媲美。在时间上，同样运行在CPU上时，VoxelMorph平均比ANTs快150倍，比NiftyReg快40倍。

模型的配准效果对比图如下：

下图是采用不同配准方法，脑部不同结构配准效果的DICE值。

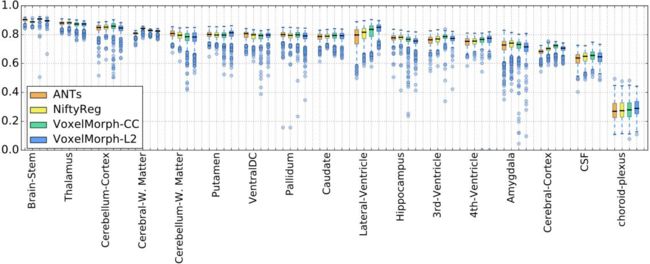
3. 实验二

实验二做了超参敏感性分析，下图展示了模型对于平滑正则参数$\lambda$的选择具有较好的鲁棒性。

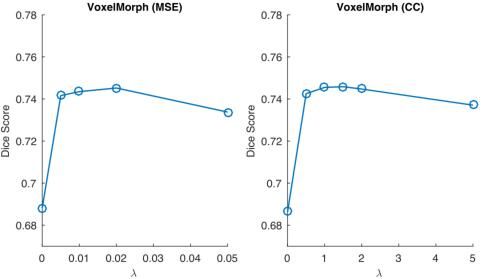
4. 实验三

实验三研究了训练集大小对效果的影响，在该部分选用的是基于MSE的VoxelMorph，使用原训练集不同大小的子集进行训练，当数据集较小时，效果会有轻微的降低，当训练集大小达到一定程度时，再增加训练集大小也不会有明显的提升。

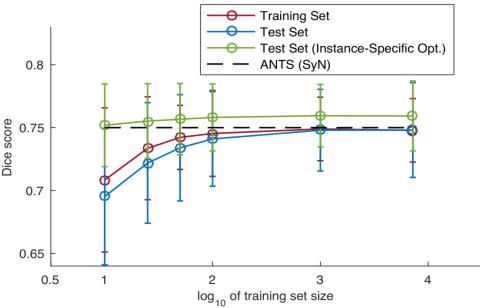
5. 实验四

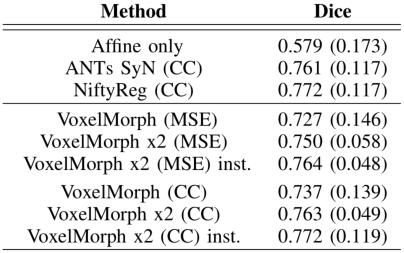
实验四展示了模型在具有人工分割标签的数据集上配准效果。在实验二基于谱图的配准模型上测试Buckner40数据集上的配准，这个数据集包含专家手工描绘的解剖结构，在这里用来评估。结果如下表，其中”inst”表示使用了特例优化的。

6. 实验五

实验五还使用随机的训练图像对作为模型的输入，并在未使用过的测试集上做测试。实组间配准，将VoxelMorph每层的特征数加倍，发现NCC损失比MSE损失更具有鲁棒性。结果如下表所示，其中$\times 2$的表示将每层特征数加倍的模型。

7. 实验六

实验六验证了使用分割标签对结果的影响，一共有30张带有分割标签的图像。使用MSE损失和$\lambda =0.02$进行训练。考虑两种情况，一种是有解剖结构标签的，另一种是有粗分割标签的。下图展示了用FreeSurfer得到分割标签和直接使用带人工分割标签的Buckner40数据集的训练情况，其中分为了只用1张图训练、用15张（一半）图训练、用30张（全部）图训练的结果。

下图是不同$\lambda$值，不同训练集下的对比结果。