NNDL 作业10：第六章课后题（LSTM | GRU）

习题6-3 当使用公式(6.50)作为循环神经网络得状态更新公式时，分析其可能存在梯度爆炸的原因并给出解决办法.

公式(6.50)为：

原因：在计算公式6.34中的误差项时，梯度可能过大，从而导致梯度过大问题。

解决办法：使用长短期记忆神经网络。

习题6-4 推导LSTM网络中参数的梯度，并分析其避免梯度消失的效果

习题6-5 推导GRU网络中参数的梯度，并分析其避免梯度消失的效果

 

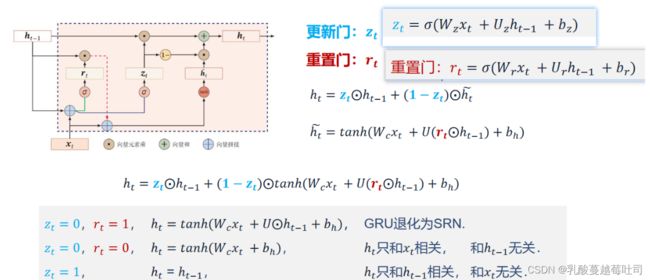
 GRU它引⼊了重置⻔（reset gate）和更新⻔（update gate) 的概念，从而修改了循环神经⽹络中隐藏状态的计算⽅式。GRU的优点是这是个更加简单的模型，所以更容易创建一个更大的网络，而且它只有两个门，在计算性上也运行得更快，然后它可以扩大模型的规模。

附加题 6-1P 什么时候应该用GRU? 什么时候用LSTM?

LSTM和GRU的不同体现在：

1.对memory 的控制

• LSTM： 用output gate 控制，传输给下一个unit
• GRU：直接传递给下一个unit，不做任何控制

2.input gate 和reset gate 作用位置不同

• LSTM: 计算new memory Ĉt时不对上一时刻的信息做任何控制，而是用forget gate独立的实现这一点
• GRU: 计算new memory 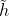t时利用reset gate 对上一时刻的信息 进行控制

3.参数数量

• GRU的参数量少，减少过拟合的风险：GRU只使用两个门控开关，达到了和LSTM接近的结果
• LSTM的参数量是Navie RNN的4倍（看公式），参数量过多就会存在过拟合的风险

 

附加题 6-2P LSTM BP推导，并用Numpy实现

 

import numpy as np
import torch
 
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
 
class LSTMCell:
    def __init__(self, weight_ih, weight_hh, bias_ih, bias_hh):
        self.weight_ih = weight_ih
        self.weight_hh = weight_hh
        self.bias_ih = bias_ih
        self.bias_hh = bias_hh
 
        self.dc_prev = None
        self.dh_prev = None
 
        self.weight_ih_grad_stack = []
        self.weight_hh_grad_stack = []
        self.bias_ih_grad_stack = []
        self.bias_hh_grad_stack = []
 
        self.x_stack = []
        self.dx_list = []
        self.dh_prev_stack = []
 
        self.h_prev_stack = []
        self.c_prev_stack = []
 
        self.h_next_stack = []
        self.c_next_stack = []
 
        self.input_gate_stack = []
        self.forget_gate_stack = []
        self.output_gate_stack = []
        self.cell_memory_stack = []
    def __call__(self, x, h_prev, c_prev):
        a_vector = np.dot(x, self.weight_ih.T) + np.dot(h_prev, self.weight_hh.T)
        a_vector += self.bias_ih + self.bias_hh
 
        h_size = np.shape(h_prev)[1]
        a_i = a_vector[:, h_size * 0:h_size * 1]
        a_f = a_vector[:, h_size * 1:h_size * 2]
        a_c = a_vector[:, h_size * 2:h_size * 3]
        a_o = a_vector[:, h_size * 3:]
 
        input_gate = sigmoid(a_i)
        forget_gate = sigmoid(a_f)
        cell_memory = np.tanh(a_c)
        output_gate = sigmoid(a_o)
 
        c_next = (forget_gate * c_prev) + (input_gate * cell_memory)
        h_next = output_gate * np.tanh(c_next)
 
        self.x_stack.append(x)
 
        self.h_prev_stack.append(h_prev)
        self.c_prev_stack.append(c_prev)
 
        self.c_next_stack.append(c_next)
        self.h_next_stack.append(h_next)
 
        self.input_gate_stack.append(input_gate)
        self.forget_gate_stack.append(forget_gate)
        self.output_gate_stack.append(output_gate)
        self.cell_memory_stack.append(cell_memory)
 
        self.dc_prev = np.zeros_like(c_next)
        self.dh_prev = np.zeros_like(h_next)
 
        return h_next, c_next
 
    def backward(self, dh_next):
        x_stack = self.x_stack.pop()
 
        h_prev = self.h_prev_stack.pop()
        c_prev = self.c_prev_stack.pop()
 
        c_next = self.c_next_stack.pop()
 
        input_gate = self.input_gate_stack.pop()
        forget_gate = self.forget_gate_stack.pop()
        output_gate = self.output_gate_stack.pop()
        cell_memory = self.cell_memory_stack.pop()
 
        dh = dh_next + self.dh_prev
 
        d_tanh_c = dh * output_gate * (1 - np.square(np.tanh(c_next)))
        dc = d_tanh_c + self.dc_prev
 
        dc_prev = dc * forget_gate
        self.dc_prev = dc_prev
 
        d_input_gate = dc * cell_memory
        d_forget_gate = dc * c_prev
        d_cell_memory = dc * input_gate
 
        d_output_gate = dh * np.tanh(c_next)
 
        d_ai = d_input_gate * input_gate * (1 - input_gate)
        d_af = d_forget_gate * forget_gate * (1 - forget_gate)
        d_ao = d_output_gate * output_gate * (1 - output_gate)
        d_ac = d_cell_memory * (1 - np.square(cell_memory))
 
        da = np.concatenate((d_ai, d_af, d_ac, d_ao), axis=1)
 
        dx = np.dot(da, self.weight_ih)
        dh_prev = np.dot(da, self.weight_hh)
        self.dh_prev = dh_prev
 
        self.dx_list.insert(0, dx)
        self.dh_prev_stack.append(dh_prev)
 
        self.weight_ih_grad_stack.append(np.dot(da.T, x_stack))
        self.weight_hh_grad_stack.append(np.dot(da.T, h_prev))
 
        db = np.sum(da, axis=0)
        self.bias_ih_grad_stack.append(db)
        self.bias_hh_grad_stack.append(db)
 
        return dh_prev
 
 
np.random.seed(123)
torch.random.manual_seed(123)
np.set_printoptions(precision=6, suppress=True)
 
lstm_torch = torch.nn.LSTMCell(2, 3).double()
lstm_numpy = LSTMCell(lstm_torch.weight_ih.data.numpy(),
                      lstm_torch.weight_hh.data.numpy(),
                      lstm_torch.bias_ih.data.numpy(),
                      lstm_torch.bias_hh.data.numpy())
 
x_numpy = np.random.random((4, 2))
x_torch = torch.tensor(x_numpy, requires_grad=True)
 
h_numpy = np.random.random((4, 3))
h_torch = torch.tensor(h_numpy, requires_grad=True)
 
c_numpy = np.random.random((4, 3))
c_torch = torch.tensor(c_numpy, requires_grad=True)
 
dh_numpy = np.random.random((4, 3))
dh_torch = torch.tensor(dh_numpy, requires_grad=True)
 
h_numpy, c_numpy = lstm_numpy(x_numpy, h_numpy, c_numpy)
h_torch, c_torch = lstm_torch(x_torch, (h_torch, c_torch))
h_torch.backward(dh_torch)
 
dh_numpy = lstm_numpy.backward(dh_numpy)
 
print("h_numpy :\n", h_numpy)
print("h_torch :\n", h_torch.data.numpy())
 
print("---------------------------------")
print("c_numpy :\n", c_numpy)
print("c_torch :\n", c_torch.data.numpy())
 
print("---------------------------------")
print("dx_numpy :\n", np.sum(lstm_numpy.dx_list, axis=0))
print("dx_torch :\n", x_torch.grad.data.numpy())
 
print("---------------------------------")
print("w_ih_grad_numpy :\n",
      np.sum(lstm_numpy.weight_ih_grad_stack, axis=0))
print("w_ih_grad_torch :\n",
      lstm_torch.weight_ih.grad.data.numpy())
 
print("---------------------------------")
print("w_hh_grad_numpy :\n",
      np.sum(lstm_numpy.weight_hh_grad_stack, axis=0))
print("w_hh_grad_torch :\n",
      lstm_torch.weight_hh.grad.data.numpy())
 
print("---------------------------------")
print("b_ih_grad_numpy :\n",
      np.sum(lstm_numpy.bias_ih_grad_stack, axis=0))
print("b_ih_grad_torch :\n",
      lstm_torch.bias_ih.grad.data.numpy())
 
print("---------------------------------")
print("b_hh_grad_numpy :\n",
      np.sum(lstm_numpy.bias_hh_grad_stack, axis=0))
print("b_hh_grad_torch :\n",
      lstm_torch.bias_hh.grad.data.numpy())

结果：

h_numpy :
 [[ 0.055856  0.234159  0.138457]
 [ 0.094461  0.245843  0.224411]
 [ 0.020396  0.086745  0.082545]
 [-0.003794  0.040677  0.063094]]
h_torch :
 [[ 0.055856  0.234159  0.138457]
 [ 0.094461  0.245843  0.224411]
 [ 0.020396  0.086745  0.082545]
 [-0.003794  0.040677  0.063094]]
---------------------------------
c_numpy :
 [[ 0.092093  0.384992  0.213364]
 [ 0.151362  0.424671  0.318313]
 [ 0.033245  0.141979  0.120822]
 [-0.0061    0.062946  0.094999]]
c_torch :
 [[ 0.092093  0.384992  0.213364]
 [ 0.151362  0.424671  0.318313]
 [ 0.033245  0.141979  0.120822]
 [-0.0061    0.062946  0.094999]]
---------------------------------
dx_numpy :
 [[-0.144016  0.029775]
 [-0.229789  0.140921]
 [-0.246041 -0.009354]
 [-0.088844  0.036652]]
dx_torch :
 [[-0.144016  0.029775]
 [-0.229789  0.140921]
 [-0.246041 -0.009354]
 [-0.088844  0.036652]]
---------------------------------
w_ih_grad_numpy :
 [[-0.056788 -0.036448]
 [ 0.018742  0.014428]
 [ 0.007827  0.024828]
 [ 0.07856   0.05437 ]
 [ 0.061267  0.045952]
 [ 0.083886  0.0655  ]
 [ 0.229755  0.156008]
 [ 0.345218  0.251984]
 [ 0.430385  0.376664]
 [ 0.014239  0.011767]
 [ 0.054866  0.044531]
 [ 0.04654   0.048565]]
w_ih_grad_torch :
 [[-0.056788 -0.036448]
 [ 0.018742  0.014428]
 [ 0.007827  0.024828]
 [ 0.07856   0.05437 ]
 [ 0.061267  0.045952]
 [ 0.083886  0.0655  ]
 [ 0.229755  0.156008]
 [ 0.345218  0.251984]
 [ 0.430385  0.376664]
 [ 0.014239  0.011767]
 [ 0.054866  0.044531]
 [ 0.04654   0.048565]]
---------------------------------
w_hh_grad_numpy :
 [[-0.037698 -0.048568 -0.021069]
 [ 0.016749  0.016277  0.007556]
 [ 0.035743  0.02156   0.000111]
 [ 0.060824  0.069505  0.029101]
 [ 0.060402  0.051634  0.025643]
 [ 0.068116  0.06966   0.035544]
 [ 0.168965  0.217076  0.075904]
 [ 0.248277  0.290927  0.138279]
 [ 0.384974  0.401949  0.167006]
 [ 0.015448  0.0139    0.005158]
 [ 0.057147  0.048975  0.022261]
 [ 0.057297  0.048308  0.017745]]
w_hh_grad_torch :
 [[-0.037698 -0.048568 -0.021069]
 [ 0.016749  0.016277  0.007556]
 [ 0.035743  0.02156   0.000111]
 [ 0.060824  0.069505  0.029101]
 [ 0.060402  0.051634  0.025643]
 [ 0.068116  0.06966   0.035544]
 [ 0.168965  0.217076  0.075904]
 [ 0.248277  0.290927  0.138279]
 [ 0.384974  0.401949  0.167006]
 [ 0.015448  0.0139    0.005158]
 [ 0.057147  0.048975  0.022261]
 [ 0.057297  0.048308  0.017745]]
---------------------------------
b_ih_grad_numpy :
 [-0.084682  0.032588  0.046412  0.126449  0.111421  0.139337  0.361956
  0.539519  0.761838  0.027649  0.103695  0.099405]
b_ih_grad_torch :
 [-0.084682  0.032588  0.046412  0.126449  0.111421  0.139337  0.361956
  0.539519  0.761838  0.027649  0.103695  0.099405]
---------------------------------
b_hh_grad_numpy :
 [-0.084682  0.032588  0.046412  0.126449  0.111421  0.139337  0.361956
  0.539519  0.761838  0.027649  0.103695  0.099405]
b_hh_grad_torch :
 [-0.084682  0.032588  0.046412  0.126449  0.111421  0.139337  0.361956
  0.539519  0.761838  0.027649  0.103695  0.099405]

Process finished with exit code 0 

总结：本次实验根据上次的BPPT推导而来，感觉比BPTT难，很费时间；在课下自学了GRU后又手推了GRU的梯度，对GRU有了一个很详细的了解，感觉GRU和LSTM连接很紧密，我觉得核心是差不多的。

参考：

LSTM如何解决梯度消失或爆炸的？ 

解决梯度消失梯度爆炸强力推荐的一个算法-----GRU（门控循环神经⽹络）

深度学习-LSTM与GRU