机器学习笔记之概率图模型(一)背景介绍

引言

从本节开始将介绍概率图模型。

背景介绍

概率图模型(Probabilistic Graphical Model)并不是指具体的某一种模型，而是一种抽象的模型思想。
这里的图(Graph)和数据结构中的图结构基本相同，只是概率图中的图 是描述概率模型内各数据特征之间关系的一种工具。
换句话说，我们将数据结构中图的结点和边之间的组合赋予概率的意义。将概率模型的一些特点用图的形式表现出来。

这里的概率自然指的是概率模型(Probabilistic Model)。在机器学习中，它提供了一种描述框架，将现实问题(学习任务)归结于基于概率的抽象(计算目标变量，如标签变量对应的概率分布结果)。

而在真实环境中，我们面临的变量可能是复杂的，具体表现在我们面临的数据可能包含高维特征。因此，我们在对随机变量进行假设时，通常将其设定为高维随机变量：
$$\mathcal{X}={\left(x^{(1)},x^{(2)},\cdots ,x^{(N)}\right)}^T={\left(\begin{array}{c}{x}_1^{(1)},x_2^{(1)},\cdots ,x_p^{(1)}\\ x_1^{(2)},x_2^{(2)},\cdots ,x_p^{(2)}\\ ⋮\\ x_1^{(N)},x_2^{(N)},\cdots ,x_p^{(N)}\end{array}\right)}_{N\times p}\to x^{(i)}\in {\mathbb{R}}^p,i=1,2,\cdots ,N$$

在最开始的极大似然估计与最大后验概率估计中介绍的，我们可以将数据集合$\mathcal{X}$看做成概率模型$\mathcal{P}(\mathcal{X})$中产生出的$N$个样本所组成的集合。
这里将$P(\mathcal{X};\theta )$中的$\theta$省略掉，因为并不是使用‘频率学派’的角度考虑该问题。
由于数据集合$\mathcal{X}$共包含$p$个维度，因此概率模型$\mathcal{P}(\mathcal{X})$的概率密度函数表示如下：
$$\mathcal{P}(x_1,x_2,\cdots ,x_p)$$
上述式子我们可以将其看做样本各维度的联合概率分布。在已知概率密度函数的条件下，我们可以求解如下信息：

• 关于样本特征的边缘概率分布：
  $$\mathcal{P}(x_i)i\in \{1,2,\cdots ,p\}$$
• 关于样本特征的条件概率分布：
  $$\mathcal{P}(x_j\mid x_i)i,j\in \{1,2,\cdots ,p\};i\ne j$$

在概率计算的过程中，包含几个重要法则：

• 概率的加法运算：
  加法运算本质上就是‘积分运算’，针对随机变量的离散、连续性有不同的表示形式。下面以离散型随机变量为例。
  $$\mathcal{P}(x_i)=\sum _{x_1,\cdots ,x_{i-1},x_{i+1},\cdots ,x_p}\mathcal{P}(x_1,x_2,\cdots ,x_p)$$
• 概率的乘法运算：
  条件概率公式~
  $$\mathcal{P}(x_1,\dots ,x_p)=\mathcal{P}(x_1\mid x_2,\cdots ,x_p)\cdot \mathcal{P}(x_2,\cdots ,x_p)$$
• 链式法则(Chain Rule)：
  $$\begin{array}{rl}\mathcal{P}(x_1,\cdots ,x_p)& =\mathcal{P}(x_1\mid x_2,\cdots ,x_p)\cdot \mathcal{P}(x_2,\cdots ,x_p)\\ & =\mathcal{P}(x_1\mid x_2,\cdots ,x_p)\cdot \mathcal{P}(x_2\mid x_3,\cdots ,x_p)\cdot \mathcal{P}(x_3,\cdots ,x_p)\\ & =\cdots \\ & =\mathcal{P}(x_1)\cdot \prod _2^{p}p(x_i\mid x_1,\cdots ,x_{i-1})\end{array}$$
• 贝叶斯法则(Bayes’ Rule)：
  上述式子有点长，这里使用2维特征$x_1,x_2$进行表示。
  $$\begin{array}{rl}\mathcal{P}(x_2\mid x_1)& =\frac{\mathcal{P}(x_1,x_2)}{\mathcal{P}(x_1)}\\ & =\frac{\mathcal{P}(x_1,x_2)}{{\sum }_{x_2}\mathcal{P}(x_1,x_2)}\\ & =\frac{\mathcal{P}(x_2)\cdot \mathcal{P}(x_1\mid x_2)}{{\sum }_{x_2}\left[\mathcal{P}(x_2)\cdot \mathcal{P}(x_1\mid x_2)\right]}\end{array}$$

联合概率分布的求解困境

关于联合概率分布$\mathcal{P}(x_1,\cdots ,x_p)$的计算困境：
当维度过高的情况下，$\mathcal{P}(x_1,\cdots ,x_p)$的 计算量极高，因为在上述公式中，我们要考虑 任意两个特征之间都可能存在关联关系。

针对上述问题，衍生出如下几种简化方式：

• 简化方式1：假设各维度之间相互独立。即：
  $$\mathcal{P}(x_1,x_2,\cdots ,x_p)=\prod _{i=1}^p\mathcal{P}(x_i)$$
  与其对应的概率图模型是朴素贝叶斯模型(Naive Bayes Model)。之前介绍过的朴素贝叶斯分类器(Naive Bayes Classifier)就是该模型的表达。
  $$\mathcal{P}(\mathcal{X}\mid \mathcal{Y})=\prod _{i=1}^p\mathcal{P}(x_i\mid \mathcal{Y})$$
  但与之对应的是朴素贝叶斯分类器针对样本特征极强的规则限制性。在真实环境中，样本基于高维特征，并且各特征之间相互独立的情况是基本不存在的。
  因此，基于上述假设，我们尝试降低对于规则的限制。

• 简化方法2：马尔可夫性质(Markov Property)，即隐马尔可夫模型中介绍的齐次马尔可夫假设：
  当一个随机过程在给定现在状态以及所有过去状态的情况下，其未来条件概率分布仅依赖于当前状态。使用数学符号表示如下：
  这里以‘一阶齐次马尔可夫假设为例’。
  $$x_{i+1}\perp x_j\mid x_{i}j<i$$
  相比于朴素贝叶斯模型的假设，马尔可夫性质 虽然降低了规则的限制强度。但不可否认，该假设规则的强度依然很高：

  这使得马尔可夫假设使模型变成了一个没有记忆的模型：只和前一个状态(1阶)相关，和其他状态的结果无关，该模型更新的信息是局限的。

  示例：
  某一阶马尔可夫链表示如下：
  
  根据齐次马尔可夫假设，$i_3$只和$i_2$相关，$i_2$只和$i_1$相关。但真实情况是：$i_3$有可能也和$i_1$相关，但因齐次马尔可夫假设的约束被抹除了。

条件独立性假设

针对马尔可夫性质的约束性，我们不妨将限制继续放宽：马尔可夫链中各节点之间的关联关系可能存在某种规律，给定某一堆节点的条件下，可能存在某一堆节点内部相互关联，另一堆节点之间内部存在相互关联，但两堆节点之间没有关联。

数学符号表示如下：
已知存在3个随机变量集合$x_{\mathcal{A}},x_{\mathcal{B}},x_{\mathcal{C}}$满足如下关系：
$$x_{\mathcal{A}}\perp x_{\mathcal{B}}\mid x_{\mathcal{C}}$$

其中$x_{\mathcal{A}},x_{\mathcal{B}},x_{\mathcal{C}}$是三个不相交的特征集合。
只需要记住：条件独立性假设划分的特征集合的内部特征只存在于唯一一个特征集合中。
而概率图模型需要表现出样本特征的条件独立性。换句话说，条件独立性需要在概率图模型中得到映射。

概率图的分类

一个概率图涉及三大部分信息：图的表示(Representation)，推断(Inference)，学习(Learning)。

• 图的表示：
  图的表示主要分有向图和无向图：

  • 基于有向图的概率图模型又称贝叶斯网络(Bayesian Network)，也称信念网络(Belief Network)。它借助有向无环图来刻画 特征之间的关联关系。

    假设存在如下贝叶斯网络结构：
    西瓜书-P157页。
    
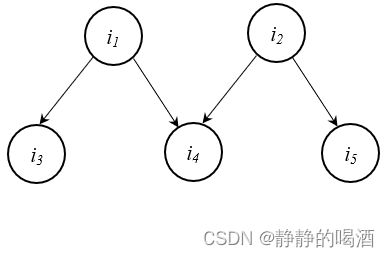
    按照书中的要求，上述每个节点内部均只包含一个特征，基于该图，五个节点的联合概率分布表示如下：
    $$\mathcal{P}(i_1,i_2,i_3,i_4,i_5)=\mathcal{P}(i_1)\cdot \mathcal{P}(i_2)\cdot \mathcal{P}(i_3\mid i_1)\cdot \mathcal{P}(i_4\mid i_1,i_2)\cdot \mathcal{P}(i_5\mid i_2)$$
    在有向图中，边表示各节点之间有向的条件概率关系。

  • 基于无向图的概率图模型又称马尔可夫网络(Markov Network)，也称马尔可夫随机场(Markov Random Field)。使用无向边表示变量间的相关关系。

• 推断过程：
  我们在变分推断系列中介绍过，推断本身是基于可观测变量推测未知变量的条件分布，这个未知变量可能是隐变量，也有可能是模型参数信息。

  推断主要分精确推断和近似推断两大部分：

  • 精确推断：变量消去法，信念传播(本系列主要介绍的推断方式)；
  • 近似推断：变分推断，马尔可夫链蒙特卡洛方法

• 学习过程：其本质是给定数据集合，以及概率图模型的形状，求解模型参数的过程，同样包含两大部分：

  • 关于含隐变量的学习过程，详见EM算法处理隐马尔可夫模型的学习问题
  • 基于完备数据的学习过程。

总结

对于概率图模型：

• 第一需要注意的是节点的意义：表示一个或者一组随机变量，也可以看成样本集合中一个或者若干个维度组成的集合；
• 第二需要注意的是概率图模型的核心是展现出样本特征的条件独立性。

下一节将介绍贝叶斯网络(有向图)。

相关参考：
马尔可夫性质-百度百科
机器学习——周志华著
机器学习-概率图模型-背景介绍