CSR-DCF(Discriminative Correlation Filter with Channel and Spatial Reliability) 文章分析（一）

CSR-DCF(Discriminative Correlation Filter with Channel and Spatial Reliability) 文章分析（一）

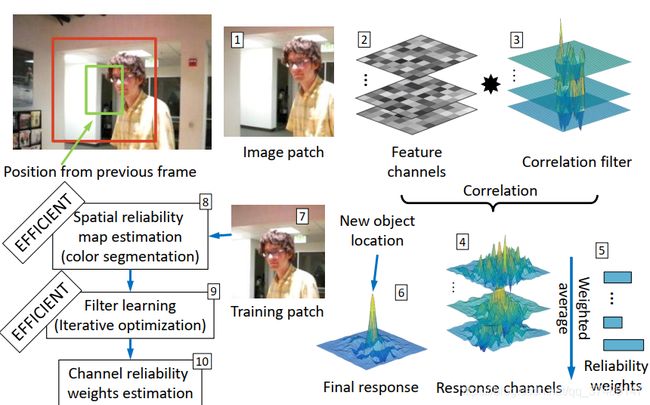
  首先作者在 DCF 的框架基础上，主要做了两点改进：

1. 引入空间置信度（Spatial Reliability）,在空间上从给滤波器加mask矩阵的角度去抑制边界效应，mask矩阵是通过前景背景的颜色直方图构建。这样处理的好处：抑制边界效应；增大搜索范围；增强对于非矩形目标的跟踪。
2. 引入信道置信度（Channel Reliability），

  通过实验，作者指出在标准 DCF 跟踪框架上，通过 HoGs 和 Colornames 两种特征表现出较好的性能。

DCF框架带来的问题

1. 首先因为DCF中引入了循环矩阵（Circulant Matrices）,限制了 filter 和 patch 大小必须相同（通过循环矩阵在傅里叶域中进行逐元素相乘，对原始卷积问题进行加速运算），由于取样的数量不能太多，因此也就限制了目标检测区域的大小。

2. 再者由于用样本矩阵的循环移位生成新的训练样本，这虽然使得样本增多，但也使训练样本大多数是无效的，因为目标的移位，可能会使得目标被分割（边界效应）。这些无效的样本并不能带来正面的训练和学习效果。
   Hamed Kiani提出的基于灰度特征MOSSE的 CFLM Correlation Filters with Limited Boundaries 和基于HOG特征的BACF，主要思路是采用较大尺寸的检测patch和较小尺寸滤波器来提高真实样本的比例，或者说滤波器填充0以保持和检测图像一样大：
   （推荐：https://blog.csdn.net/u012154840/article/details/73089430）

3. 另一个限制是对于检测目标形状的假设：

“Another limitation of the published DCF methods is the assumption that the target shape is well approximated by an axis-aligned rectangle.”

  对于形状不规则和中空的目标，DCF filter 会因为背景的学习导致追踪漂移和失败，近似矩形的目标在遮挡的情况下也会出现相同的问题。M. Danelljan 提出的 SRDCF 中也存在这样的问题。

本文针对上述问题的改进

1. 利用前景/背景的颜色模型构建了 spatial reliability map (空间置信度map，也就是 mask 矩阵)用于对滤波器的空域限制，并给出了求解方法。
   空间置信度映射将滤波器应用（映射）于适合跟踪的目标部分，克服了循环位移不允许任意搜索范围的问题和目标矩形形状假设的局限性。并且提出一种求解该问题的优化算法。

2. Channel reliability (通道置信度)，利用不同通道的置信度信息构建了不同通道的加权系数，即通道的可靠性系数；

3. 作者提出的置信度框架可被推广至绝大多数的相关滤波器设计中。

Spatially constrained correlation filters

  作者将滤波器 $h$ 按照特征通道划分为每个通道相互独立的
$h_d$，$h=\{h_d{\}}_{d=1:N_d}$，特征也对应被分为$f_d$，$f=\{f_d{\}}_{d=1:N_d}$，每帧的mask矩阵是共享的，最后检测计算响应也是各通道分布算个响应加起来，然而每个通道的重要性是不一样的，有必要对每个通道加权，这里考虑给滤波器h加权。作者认为这个权重应该由两项构成，分别为学习可靠性和检测可靠性。
  在已知 $h$, $f$ 时，检测目标中心处于 $x$ 处的最大概率如下：
$$p(x|h)=\sum _{d=1}^{N_d}p(x|f_d)p(f_d).(1)$$
其中， $p(x|f_d)=[f_d\ast h_d](x)$ ,也就是每个通道的响应值；$p(f_d)$ 是反应通道置信度的先验。

  要优化的问题：

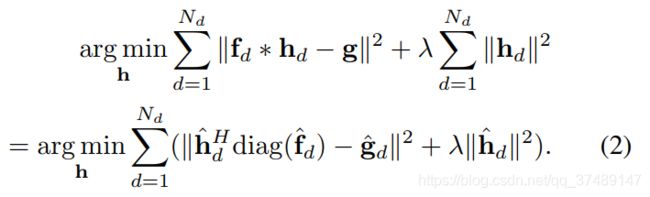
  由于 Parsevaal 定理（函数平方的和或积分等于其傅里叶转换式平方之和或者积分），又因为 $f_d$ 是循环矩阵，因此可以被对角化加速计算（KCF中得出结论），因此公式（2）成立。

Constructing spatial reliability map

  线性空间下patch边缘的部分可信度不高，这是由于循环样本导致的. SRDCF中对滤波器 $h$ 进行限制，加上倒高斯的权重; BACF中直接用真实样本然后和只有中间部分有值边缘都是0的mask矩阵进行限制。
  这两者都是以目标为中心，遵循规则目标的限制，没有针对目标的具体形状，所以作者考虑加上一个和目标有关的不规则mask来限制边界效应。

  Spatial reliability map 矩阵 $m\in [0,1{]}^{d_w\ast d_h}$ ,其中每个元素均为0或1，也就是在已知 $x,y$ 条件下，求当前像素块是前景的概率。
   公式（3）等式左边可以使用贝叶斯展开：
$$p(m=1|y,x)=\frac{p(m=1,x,y)}{p(x,y)}=\frac{p(m=1)p(x|m=1)p(y|x,m=1)}{p(x,y)}.(4)$$
在已知 $x,y$ 条件下，$p(x,y)$ 相当于常数。
  $p(y|m=1,x)$ 是目标的外观似然估计，作者用了前景和背景的颜色直方图 $c=\{c^f,c^b\}$ 计算。$p(m=1)$ 是根据提取的前景、背景模型的大小比值来决定。
  这里作者做了一个弱先验的假设，表示目标空间位置的似然估计，
$$p(x|m=1)=k(x;\sigma ).(5)$$
  其中 $k(x;\sigma )$ 是 Epanechnikov kernel ，$k(x;\sigma )=1-(\frac{\gamma }{\sigma }{)}^2$, 核函数参数 $\sigma$ 对应最小边界框，并将其限制在 $[0.5,0.9]$, 最终使得使目标先验概率中心处大小为0.9，远离中心的为均匀分布。这样做是为了避免目标外观发生显著性变化时，算法做出一些潜在的不良分类，当被分类为背景的像素比值小于最小值 ${\alpha }_{min}$ 时，目标边界框内部被假设为一个均匀分布。

   上图中背景直方图和前景直方图需要在每一帧中更新。
   在作者的另一篇论文 Discriminative Correlation Filter Tracker with Channel and Spatial Reliability 中，作者这样解释：记目标前/背景颜色直方图 $c=\{c^f,c^b\}$ ,观测结果 $y_i=\{y_i^c,y_i^x\}$ ,其中 $y_i^c$ 表示目标训练区域内的第$i$个像素的颜色特征（颜色信息），$y_i^x$ 表示它的位置特征（位置信息），$m_i\in \{0,1\}$,表示当前像素属于前景或者背景。
$$p(y_i)=\sum _{j=0}^{1}p(y_i│m_i=j)p(m_i=j)$$ $={\sum }_{j=0}^{1}p(y_i^c│m_i=j)p(y_i^x│m_i=j)p(m_i=j)$
$=p(y_i^c│m_i=0)p(y_i^x│m_i=0)p(m_i=0)$
$+p(y_i^c│m_i=1)p(y_i^x│m_i=1)p(m_i=1)$

   上式中 p(y_i^c│m_i=j) 是目标的外观似然估计(appearance likelihood)，通过前/背景颜色模型c求解；

$p(y_i^x│m_i=j)$ 是目标的空间位置似然估计(spatial likelihood):$$p(y_i^x│m_i=j)=k(x;\sigma )=1-(\frac{r}{\sigma }{)}^2$$

$p(m_i=j)$ 是前/背景先验概率(foreground/background prior probability): $$p(m_i=j)=\frac{前景区域的大小}{背景区域的大小}$$ .

   作者文中目标的空间似然估计和外观似然估计，后验概率示意图：
   这是我自己测试的两张张图片：

Constrained correlation filter learning

   这里假设通道数为1，为了推导时更加简洁明了。mask矩阵每一帧都会提前计算好，求解限制目标函数的时候当作常量，引入对偶变量 $h_c$ 和限制 $h_c-m\odot h\equiv 0$ ，在正则项只考虑了加上mask之后的h，即 $h_m,h_m=(m\odot h).$ 使用增广拉格朗日函数法求解公式(2):

   公式（5）没有封闭解，所以只能通过迭代子问题求解，

   作者文中给出的求解过程如下：

Channel reliability estimation

   信道置信度由学习置信度和检测置信度组成，其中各通道均独立运算。

channel learning reliability

   信道学习置信度反应的是当前滤波器 filter 所能检测出目标的最大可能性，当信道学习置信度越高，说明该在该通道的可靠性越高，也就是权重越大。
   信道学习置信度 $p(f_d)$ (公式1中) 可直接通过 filter 响应最大值求得，即 $w_d=\zeta max(f_d\ast h_d)$ ,其中 $max(f_d\ast h_d)$ 是当前通道的最大响应值，$\zeta$ 是归一化权值，保证 ${\sum }_d{w}_d=1.$
  信道学习置信度应在目标定位时求出。

channel detection reliability

  信道检测置信度反应的是每个通道的响应中主峰的表达性，后面介绍作者提出的检测标准。
  MOSSE 论文中提到 PSLR (峰值旁瓣比)作为衡量检测跟丢的标准, $$PSLR：峰值旁瓣比=\frac{主瓣峰值强度}{最强旁瓣的峰值强度}.$$
  本文中作者计算次峰值和主峰值之比，比值越小，说明响应图越干净，跟踪效果越好，那么可靠性越高。
  当多个相似的对象出现在目标附近时（多个响应峰值出现），这个比例会增大，因为这个相似的目标会产生相似的分布，即使响应主峰准确地描述了目标位置。为了防止这种惩罚，这个权值w最大值被限制为0.5。
  原则上希望检测置信度越大越好（也就是两者比值越小越好）。
  检测置信度表达式：
$$w_d^{(det)}=1-min(\frac{{\rho }_{max2}}{{\rho }_{max1}},\frac{1}{2})$$
其中 ${\rho }_{max1}$ 表示第一主峰强度，${\rho }_{max2}$ 表示最强胖瓣主峰强度（第二峰强度）。

学习置信度和检测置信度两项乘积即为信道置信度。
  下图是求出各通道的响应。：

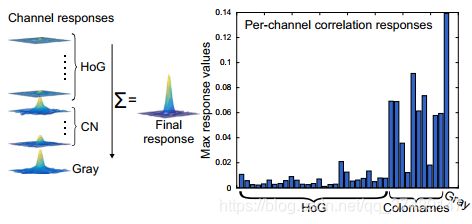
  下图是根据每个通道的响应求出学习置信度。：

Tracking with channel and spatial reliability

  先看下整个算法的流程图：

  在跟踪中如何使用这两个置信度：
定位阶段：

1. 上一帧的学习置信度需要提前求出；
2. 计算当前帧的检测置信度和每个通道的响应；
3. 用上一帧学习置信度乘于当前帧的检测置信度，得到每个通道的置信度分数；
4. 最终结果由各通道的响应加权和决定；
5. 尺度的估计是由一个一维的尺度 fliter 得出(DSST)。

学习阶段：

1. 提取预测位置的前景和背景直方图，用固定的学习率更新；
   前景直方图是在预测得出的目标 bounding box 中，利用 标准的 Epanechnikov kernel 提取得出；背景直方图是在目标两倍大小的邻域内提取。
2. 构建 空域mask矩阵；
3. 通过公式（5）得出最优 filter h;
4. 根据 3 中学得的最优滤波器 h, 求出每个通道的响应，从而计算出学习置信度；

上面两步中所有的更新方式均为自回归模型：
  以滤波器更新为例：
$$h_t=(1-\eta )h_{t-1}+\eta h$$
上述公式中出现的 $h$ 和 整体算法流程中出现的 $w，c^f，c^b$ ,均表示从当前帧得到。

另外推荐两篇博客：

1. CSR-DCF视频目标跟踪论文笔记（1）——关于似然和后验概率在分割操作中的应用：https://blog.csdn.net/discoverer100/article/details/78182306

2. CSR-DCF视频目标跟踪论文笔记（2）——关于滤波器Learning的推导（Augmented Lagrangian方法）：
   https://blog.csdn.net/discoverer100/article/details/78323934