机器学习之线性回归——OLS，岭回归，Lasso回归

线性回归

什么是线性回归呢？其实线性回归是统计学中的，线性回归（Linear Regression）是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种 回归分析 。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归，大于一个自变量情况的叫做多元回归。在线性回归中，数据使用线性预测函数来建模，并且未知的模型参数也是通过数据来估计。 这些模型就被叫做线性模型。线性模型将机器学习中有监督学习模型定义为类似如下公式的多项式函数：

$$y=w_0+w_1{x}_1+w_2{x}_2+w_3{x}_3+...+w_n{x}_n$$

线性模型学习的目的就是确定$w_0,w_1,w_2,...,w_n$的值，使得y可以根据特征值直接通过该函数计算得到。其中模型中的参数W0也称为截距(intercept)，$w_1{w}_2,w_3,...,w_n$称为回归系数(coefficient)。
判断下下面两种多项式是否为线性模型。
$$1.y=2w_0+w_1{x}^1+w_2{x}^2+w_3{x}^3+w_n{x}^n+...$$
$$2.y=w_0+sin(w_1)x_1+cos(w_2)x_2+ex{p}^{w_3{x}_3}+...$$
显然，1式最终式可以转换为线性模型的多项式的，而2式却不能。所有2式不是线性模型。从中我们可以得到这样的结论：是否为线性模型取决于其被求系数$w_0,w_1...w_n$之间是否为线性关系，与样本特征变量$x_0,x_1...x_n$的形式无关。
而对于非线性模型的学习，我们通常无法通过和线性模型那样进行固定公式的参数逼近，而需要使用之后要学习的带核函数的SVM,神经网络等更复杂的模型。

最小二乘法(OLS)

上面讲的了线性回归模型的一些简单概念，接下来实践下最简单的线性模型算法——最小二乘法(Ordinary Least Squares,OLS)。最小二乘法是通过最小化样本真值与预测值之间的方差和来达到计算出$w_1,w_2,w_3,..,w_n$的目的。就是：
$$\mathrm{argmin}(\sum (y_1-y{)}^2)$$
其中$y_1$是样本预测值，y是样本中的真值。下面使用波士顿房价数据来实践。
导入库和数据

from sklearn import linear_model
import numpy as np
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

boston = load_boston()
datas = boston.data
target = boston.target
name_data = boston.feature_names

进行简单的数据可视化，筛选特征

fig = plt.figure()
fig.set_size_inches(14, 9)
for i in range(13):
    ax = fig.add_subplot(4, 4, i+1)
    x = datas[:, i]
    y = target
    plt.title(name_data[i])
    ax.scatter(x, y)
plt.tight_layout()  # 自动调整子图间距
plt.show()

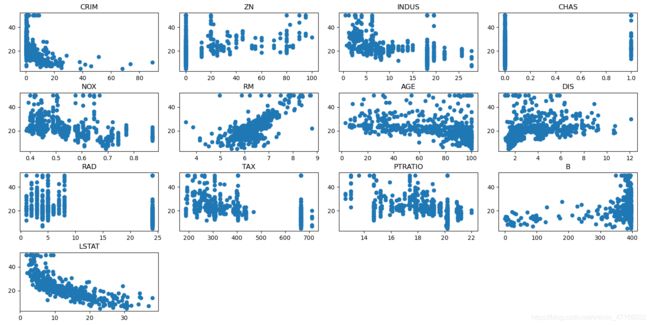
从图片可以看出，特征RM和LSTAT具有明显的相关性，且一个呈单调递增，一个呈单调递减，所以选择这两个特征进行训练。
提取特征 RM,LSTAT

j_ = []
for i in range(13):
    if name_data[i] == 'RM':
        continue
    if name_data[i] =='LSTAT':
        continue
    j_.append(i)
x_data = np.delete(datas, j_, axis=1)

接下来把处理好的数据集分为训练集和测试集，选择线性回归模型训练与预测数据。

X_train, X_test, y_train, y_test = train_test_split(x_data, target, random_state=0, test_size=0.20)
lr = linear_model.LinearRegression()
lr.fit(X_train, y_train)
lr_y_predict = lr.predict(X_test)
score = lr.score(X_test, y_test)
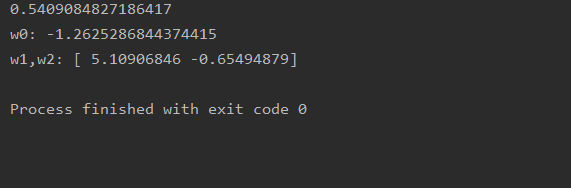
print(score)
print("w0:",lr.intercept_)
print("w1,w2:", lr.coef_)

从训练结果来看，训练的得分不是很好，只有0.5409084827186417，拟合到的线性模型是：y = -1.2625286844374415 + 5.10906846$x_1$ - 0.65494879$x_2$。

岭回归(Ridge Regression)

岭回归是俄罗斯科学家Tikhonov提出的，它通过改变回归目标函数，达到控制回归参数值随着维度疯狂增长的目的。岭回归是在OLS的基础上改进的，它的回归目标函数与普通的OLS的差别在于将$\alpha \sum w^2$加入了最小化目标，其中$\alpha$是一个可以调节的超参数，w是线性模型中的所有参数。$\alpha \sum w^2$也被称为L2惩罚项(L2 Penalty)。岭回归的目标函数是：
$$\mathrm{argmin}(\sum (y_1-y{)}^2+\alpha \sum w^2)$$

Lasso回归

Lasso回归与岭回归差别不大，Lasso回归只是把岭回归的惩罚项中的$w^2$改为了$|w|$，称为L1惩罚项。但惩罚效果却比L2严厉很多，可以产生稀疏回归参数的作用，即多数回归参数为零。它的目标函数是：
$$\mathrm{argmin}(\sum (y_1-y{)}^2+\alpha \sum |w|)$$

OLS，岭回归，Lasso回归之间对比

从目标函数可以看出，岭回归，Lasso回归都是在OLS的基础上产生的，这样看来，OLS似乎已经可以解决所有线性回归的问题了，什么还会出现岭回归，Lasso回归等模型呢？
其实是因为OLS会随着特征维度的增加，模型求得的参数$w_0,w_1,w_2,..,w_n$的值也会显著的增加。产生这个现象的原因是OLS试图最小化公式$\mathrm{argmin}(\sum (y_1-y{)}^2)$的值，因此为了拟合训练数据中很小的x值差异产生较大的y值差异，这样就必须要使用较大的w值。而越来越大的w值在测试数据上的反映的结果则是任何一个特征微小的变化都会导致最终的预测目标值大幅度变化，产生过度拟合现象。为了面对OLS在高维度数据训练存在过拟合现象，所以引入了加入惩罚项的岭回归，Lasso回归等模型。岭回归相比OLS在高维特征训练的结果来看，模型参数w的值会显著降低，并且$\alpha$参数的大小与训练结果的回归参数呈反向关系：$\alpha$越大，回归参数越小，模型越平缓。但是在岭回归模型中，无论将$\alpha$设多大，回归模型参数都只有非常小的绝对值，达不到零值。这样就造成了一个结果，可能有很多特征对最终预测结果的影响不大，但还是得将其加入模型计算中，这样会对数据的产生，存储，传输，计算等产生较大的浪费。Lasso就解决了岭回归的这样一个问题，Lasso回归可以将一个或多个不重要的特征参数值计算为零。从而减少特征参数，达到了压缩相关特征的目的。下面我们实践来看下这些差异。

# encoding = 'utf-8'
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn import linear_model

# 导入数据
data = pd.read_csv(r'C:\data\data.csv')
x_data = data.drop('y', 1)
x = x_data.drop('x11', 1)
y_data = data.loc[:, 'y']
name_data = list(data.columns.values)
# 数据预处理
train_data, test_data, train_target, test_target = train_test_split(x_data, y_data, test_size=0.3)
Stand_X = StandardScaler()  # 特征进行标准化
Stand_Y = StandardScaler()  # 标签也是数值，也需要进行标准化
train_data = Stand_X.fit_transform(train_data)
test_data = Stand_X.transform(test_data)
train_target = Stand_Y.fit_transform(train_target.values.reshape(-1, 1))  # reshape(-1,1)指将它转化为1列，行自动确定
test_target = Stand_Y.transform(test_target.values.reshape(-1, 1))
# 最小二乘法
lr = linear_model.LinearRegression()
lr.fit(train_data, train_target)
lr_y_predict = lr.predict(test_data)
score = lr.score(test_data, test_target)
print("最小二乘法：", score)
print("w0(截距):", lr.intercept_)
print("回归系数:", lr.coef_)
# 岭回归
rg = linear_model.Ridge(alpha=0.01)
rg.fit(train_data, train_target)
rg_score = rg.score(test_data, test_target)
print("*********************************************")
print("岭回归(a=0.01)：", rg_score)
print("w0(截距):", rg.intercept_)
print("回归系数:", rg.coef_)
# 岭回归
rg = linear_model.Ridge(alpha=0.1)
rg.fit(train_data, train_target)
rg_score = rg.score(test_data, test_target)
print("*********************************************")
print("岭回归(a=0.1)：", rg_score)
print("w0(截距):", rg.intercept_)
print("回归系数:", rg.coef_)
# Lasso回归
ls = linear_model.Lasso(alpha=0.01)
ls.fit(train_data, train_target)
ls_score = ls.score(test_data, test_target)
print("*********************************************")
print("LASSO回归：", ls_score)
print("w0(截距):", ls.intercept_)
print("回归系数:", ls.coef_)

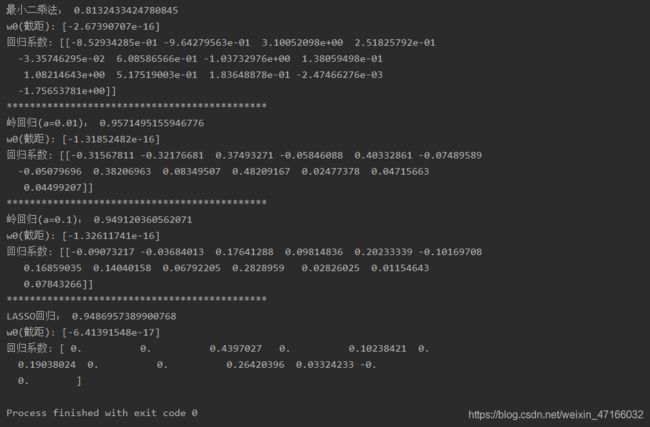
通过训练结果可以明显看出这三种模型之间的差异与在相同模型下$\alpha$值的设置不同产生不同的回归参数。最后总结下这三个模型的优缺点：

模型	优点	缺点
最小二乘法(OLS)	建模快速简单，适用于要建模的关系不是非常复杂且数据量不大的情况	特征维度高的数据下存在过拟合现象且求得的参数多
岭回归	解决了OLS在特征维度高的数据存在过拟合现象	它缩小了回归参数的值，但没有达到零，没有特征选择功能。没有解决OLS求得的参数多的缺点
Lasso回归	具有特征选择功能，同时解决了OLS过拟合和参数多的缺点	Lasso回归会使得一些绝对值较小的系数直接变为0，这就产生了它的损失函数不是连续可导的，由于L1范数用的是绝对值之和，导致损失函数有不可导的点