pytorch深度学习实战lesson26

第二十六课 GoogLeNet

       这节课学习Googlenet ， 虽然 nin 现在几乎没有被使用，但是 Googlenet 还是在大量的被使用。在比如说 Google 内部当然是用的挺多的，在外面也是被经常使用。这个网络当时候出来的时候也是吓了大家一跳。

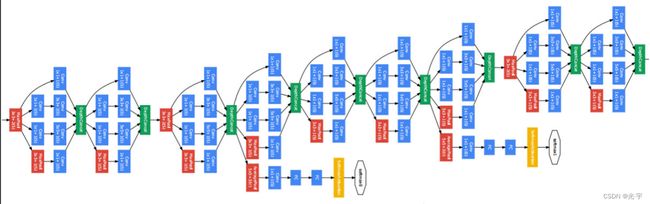
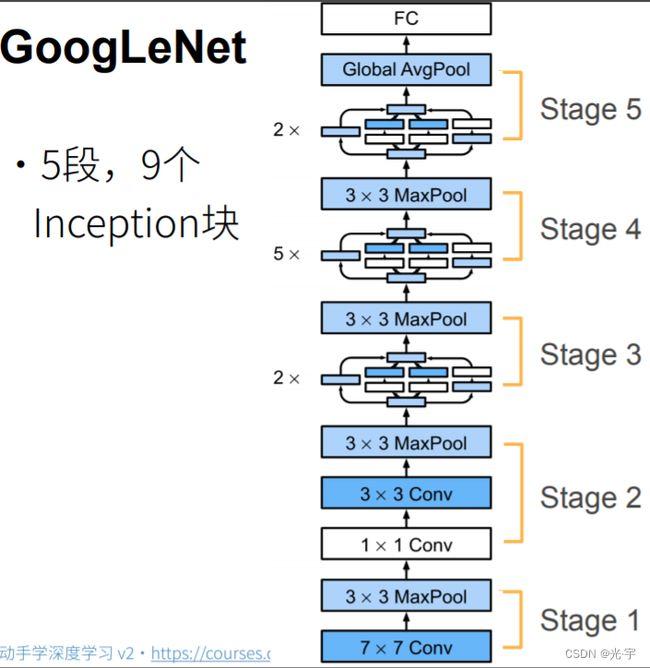
       如上图所示，它是第一次做一个几乎快到100层的卷积层。而且可以看到它的名字 L 是大写的，所以它是致敬了lenet。然后它在 IMAG net上拿了挺好的成绩，是老冠军。

目录

理论部分

实践部分

---

理论部分

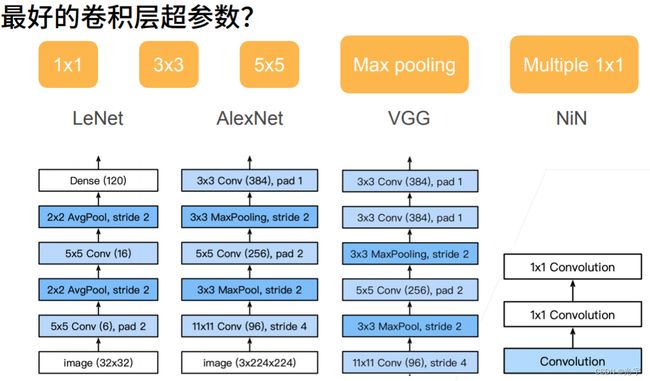
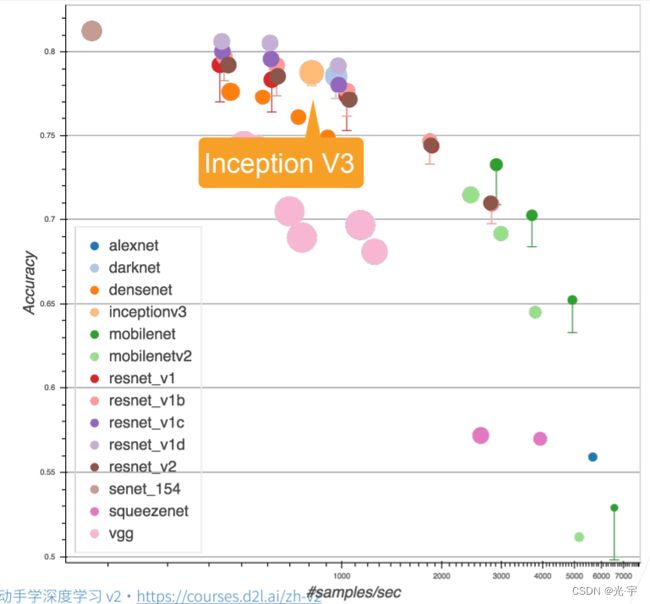
有这么多个选择，那么到底用谁比较好呢？

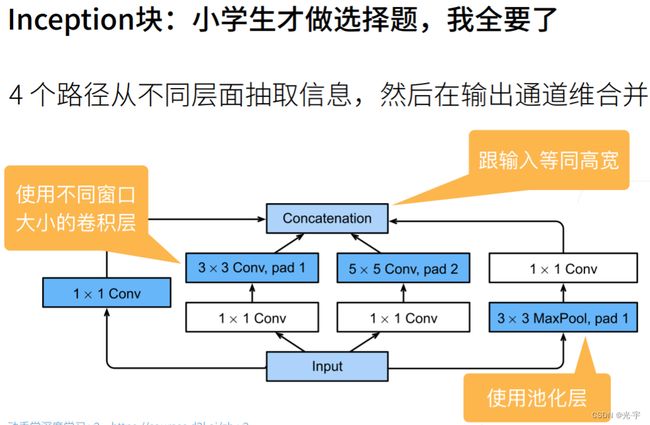
       Google net 里面最重要的叫做 inception 块，就是说你我不给你做选择，我全都要：每个块里面抽取不同的通道，然后不同通道有不同的设计，把想要的那些东西都放在里面。这就是 inception 块的想法。

       可以看到输入有四条路。第一条路是输入先接到一个1乘1的卷积层里面，再输出；然后第二条路先通过一个1乘1的卷积层对通道做变换，再输入到3乘3的卷积层里面， pad 等于1，使得输入和输出的高宽是一样的；第三条路输入又是一个1乘1的卷积层来对通道数做变换，不改变高宽。但是就是说通过一个5乘5的卷积层来做一些空间信息， pad =2：输入和输出等宽；第四路是用了一个3乘3的 max pulling， pad 等于1，然后再在后面加一个1乘1的卷积层。

       所以所有四条路的输出没有改变高宽，因此最后可以把它们合并起来。高宽不变，那变的是什么？变的其实是通道数。

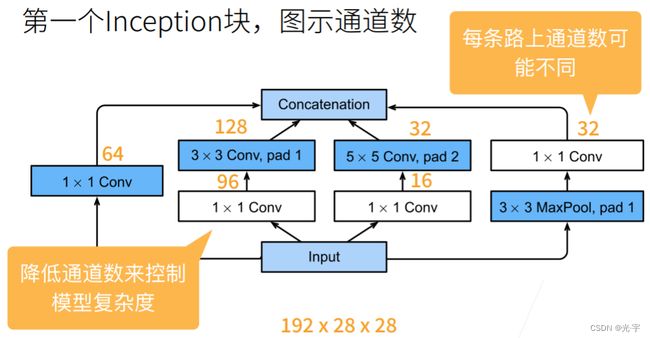
       假设输入通道数是192，高宽是28的话（不用管，反正不会变对吧）。如上图所示，我把输入通道从192变成了输出的256。这里的设计要点就在于把重要的那些参数留给我们觉得比较重要的那些通道。

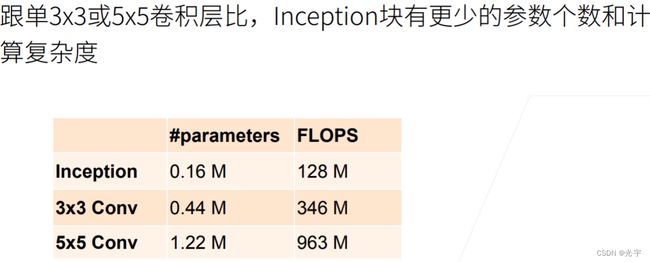
       可见inception 不仅得增加了网络层的多样性，参数数变少了，计算量也变低了，所以这也就是它的好处。

       Google net 大量使用1乘1的卷积，它很多时候也是当全连接在用(就是把通道数做变换)，第二个是它也使用了全局的平均值池化层，但不一样的是它没有一定要设计 inception block 使得最后一个 inception block 的输出通道数等于类别个数。

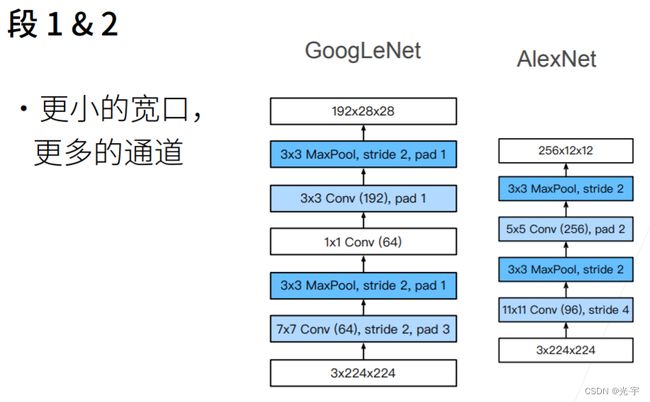
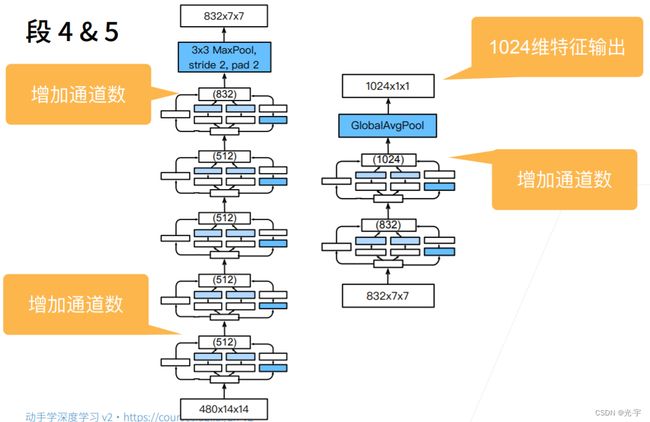
        前面两个段虽然卷积层不多，但是也可以很快的把通道拉上去，把高宽减下去，使得后面的计算可控。这一点它确实比 alexnet 还是要好一点 ，alexnet 直接降到12了，Google Net还有28乘28，所以说可以认为Google Net用了更小的卷积层，但是高宽保留的更多一点，这样使得后面能支撑更深的一些网络。

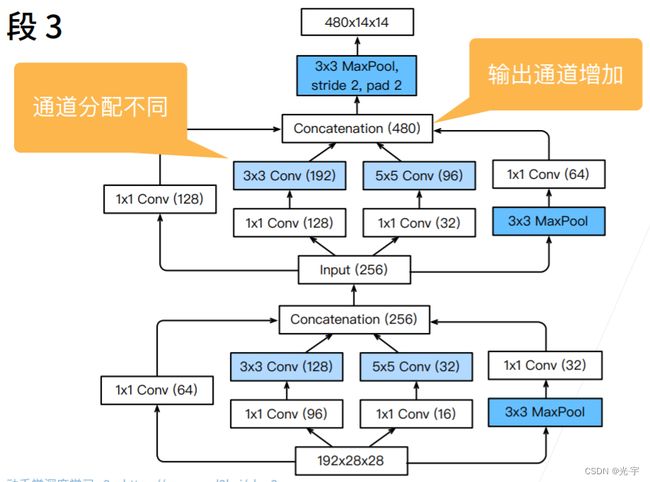
        Stage3又把通道数从输入的192扩大到了480，但是里面每个层的参数并没有什么技巧去配置，它只是说千万次的实验后才得出来的。

        段四和段五也是一样的，你根本就不知道他里面到底是怎么样算，所以导致 Google net 那个论文特别的难以复现。但总体的原则还是增加通道数，增加到了1024。是vgg的两倍。

        V 2就是加入了 bachelalization；v3 上面他又去重新去看了一下 inception block 他看了看里面还有什么样的可以调的东西；然后 v4 的话就在 v3 的基础上加入了残差连接

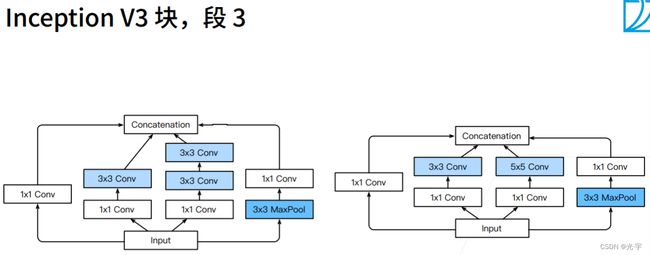
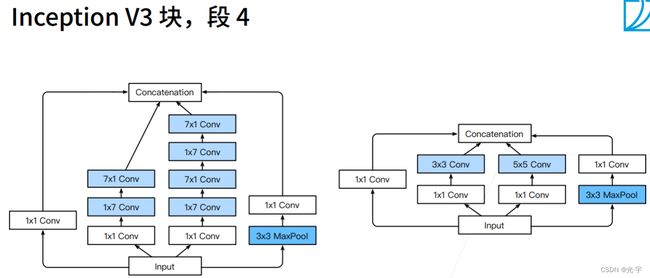
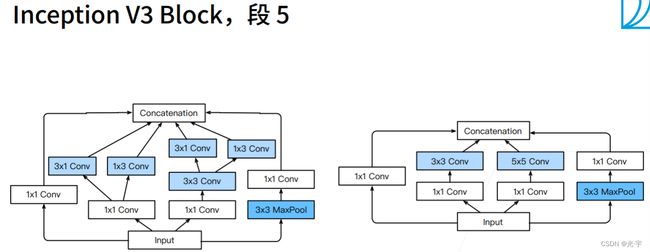
下面三张图是Googlenet对于段3,4,5比较新颖的做法，都比较奇怪。。。

        v3这个东西虽然很诡异，但是实际上效果还是挺好的。虽然速度不是很快，但是精度很理想。

实践部分

 

代码：

#含并行连结的网络（GoogLeNet）
#Inception块
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
import matplotlib.pyplot as plt
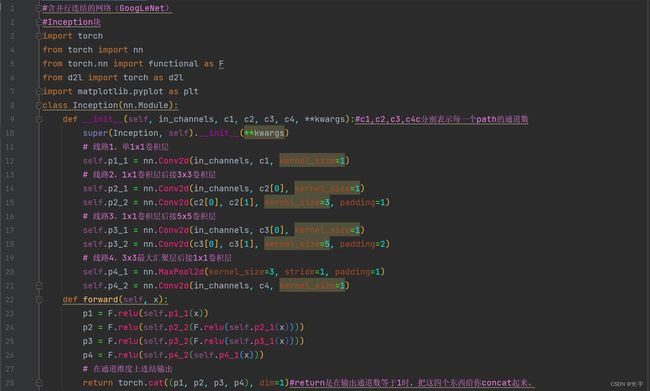
class Inception(nn.Module):
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):#c1,c2,c3,c4c分别表示每一个path的通道数
        super(Inception, self).__init__(**kwargs)
        # 线路1，单1x1卷积层
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        # 线路2，1x1卷积层后接3x3卷积层
        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1x1卷积层后接5x5卷积层
        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3x3最大汇聚层后接1x1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)
    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        # 在通道维度上连结输出
        return torch.cat((p1, p2, p3, p4), dim=1)#return是在输出通道数等于1时，把这四个东西给你concat起来。
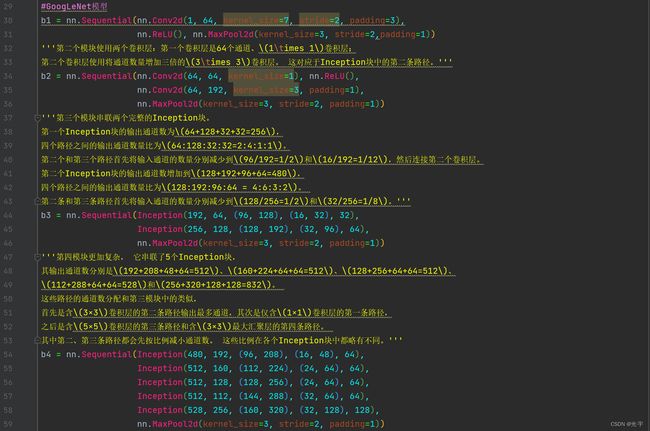
#GoogLeNet模型
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.ReLU(), nn.MaxPool2d(kernel_size=3, stride=2,padding=1))
'''第二个模块使用两个卷积层：第一个卷积层是64个通道、\(1\times 1\)卷积层；
第二个卷积层使用将通道数量增加三倍的\(3\times 3\)卷积层。 这对应于Inception块中的第二条路径。'''
b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1), nn.ReLU(),
                   nn.Conv2d(64, 192, kernel_size=3, padding=1),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
'''第三个模块串联两个完整的Inception块。 
第一个Inception块的输出通道数为\(64+128+32+32=256\)，
四个路径之间的输出通道数量比为\(64:128:32:32=2:4:1:1\)。
第二个和第三个路径首先将输入通道的数量分别减少到\(96/192=1/2\)和\(16/192=1/12\)，然后连接第二个卷积层。
第二个Inception块的输出通道数增加到\(128+192+96+64=480\)，
四个路径之间的输出通道数量比为\(128:192:96:64 = 4:6:3:2\)。 
第二条和第三条路径首先将输入通道的数量分别减少到\(128/256=1/2\)和\(32/256=1/8\)。'''
b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                   Inception(256, 128, (128, 192), (32, 96), 64),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
'''第四模块更加复杂， 它串联了5个Inception块，
其输出通道数分别是\(192+208+48+64=512\)、\(160+224+64+64=512\)、\(128+256+64+64=512\)、
\(112+288+64+64=528\)和\(256+320+128+128=832\)。 
这些路径的通道数分配和第三模块中的类似，
首先是含\(3×3\)卷积层的第二条路径输出最多通道，其次是仅含\(1×1\)卷积层的第一条路径，
之后是含\(5×5\)卷积层的第三条路径和含\(3×3\)最大汇聚层的第四条路径。 
其中第二、第三条路径都会先按比例减小通道数。 这些比例在各个Inception块中都略有不同。'''
b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                   Inception(512, 160, (112, 224), (24, 64), 64),
                   Inception(512, 128, (128, 256), (24, 64), 64),
                   Inception(512, 112, (144, 288), (32, 64), 64),
                   Inception(528, 256, (160, 320), (32, 128), 128),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
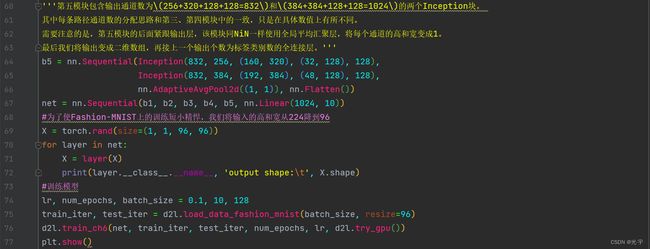
'''第五模块包含输出通道数为\(256+320+128+128=832\)和\(384+384+128+128=1024\)的两个Inception块。 
其中每条路径通道数的分配思路和第三、第四模块中的一致，只是在具体数值上有所不同。 
需要注意的是，第五模块的后面紧跟输出层，该模块同NiN一样使用全局平均汇聚层，将每个通道的高和宽变成1。 
最后我们将输出变成二维数组，再接上一个输出个数为标签类别数的全连接层。'''
b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                   Inception(832, 384, (192, 384), (48, 128), 128),
                   nn.AdaptiveAvgPool2d((1, 1)), nn.Flatten())
net = nn.Sequential(b1, b2, b3, b4, b5, nn.Linear(1024, 10))
#为了使Fashion-MNIST上的训练短小精悍，我们将输入的高和宽从224降到96
X = torch.rand(size=(1, 1, 96, 96))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__, 'output shape:\t', X.shape)
#训练模型
lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
plt.show()

Sequential output shape:     torch.Size([1, 64, 24, 24])
Sequential output shape:     torch.Size([1, 192, 12, 12])
Sequential output shape:     torch.Size([1, 480, 6, 6])
Sequential output shape:     torch.Size([1, 832, 3, 3])
Sequential output shape:     torch.Size([1, 1024])
Linear output shape:     torch.Size([1, 10])
training on cuda:0

。。。。
loss 0.238, train acc 0.909, test acc 0.894
1023.0 examples/sec on cuda:0

进程已结束,退出代码0