决策曲线 Decision Curve

本文转自：决策曲线分析法（Decision Curve Analysis，DCA）

简介

评价一种诊断方法是否好用，一般是作ROC曲线，计算AUC。但是，ROC只是从该方法的特异性和敏感性考虑，追求的是准确。而临床上，准确就足够了吗？患者就一定受益吗？

比如我通过某个生物标志物预测患者是否患了某病，无论选取哪个值为临界值，都会遇到假阳性和假阴性的可能，有时候避免假阳性受益更大，有时候则更希望能避免假阴性。既然两种情况都无法避免，那我就想要找到一个净受益最大的办法。

2006年，MSKCC（纪念斯隆凯特琳癌症研究所）的AndrewVickers博士等人研究出另一种评价方法，叫决策曲线分析法（Decision Curve Analysis，DCA）。相对于二战时期诞生的ROC曲线，DCA还很年轻，也一直在完善之中，不过2012-2016年间，Ann InternMed.、JAMA、BMJ、J Clin Oncol等杂志都已陆续发文，推荐使用决策曲线分析法。

      

      Lancet. 2016 Jun 4;387(10035):2302-11.

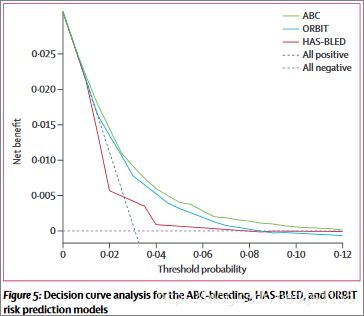
这是一个来自Lancet的例子，研究者为了评价房颤患者口服抗凝药的出血风险，开发了一种新的评价方法，即基于生物标志物的ABC出血风险评分（Age，Biomarkers，Clinicalhisory），让它和传统的ORBIT及HAS-BLED法比较。这种类型的研究，咱们通常就是作ROC曲线。但他们没有，而是采用了决策曲线分析法。

这幅图的横坐标为阈概率（ThresholdProbability）。当各种评价方法达到某个值时，患者i的出血风险概率记为Pi；当Pi达某个阈值（记为Pt），就界定为阳性，采取某种干预措施（比如更改抗凝方案）。

那么改了抗凝方案，自然就改变了出血与血栓形成之间的利弊平衡，纵坐标就是利减去弊之后的净获益率（Net Benefit, NB）。

可这幅图除了三种评价方法的曲线外，还有两条虛线，它们代表两种极端情况。横的那条表示，所有样本都是阴性（Pi < Pt），所有人都没干预，净获益为0。斜的那条表示所有样本都是阳性，所有人都接受了干预，净获益是个斜率为负值的反斜线（原理见后文）。其它的曲线就与它们相比较。

从图中可以看出，HAS-BLED曲线和两条极端曲线很接近，也就是说它没什么应用价值。而在一个很大的Pt区间范围内，ABC法和ORBIT法的获益都比极端曲线高，所以它们可选的Pt范围都比较大，相对安全。而ABC又比ORBIT好一些。

 

绘制决策曲线

毕竟这是新的算法嘛，传统的统计软件好像还木有跟上，R语言倒是跟得挺快。2016年，Kerr等人专为决策曲线制作了个名为DecisionCurve的R语言包。

这里有一份示例数据，是NHLBI（美国国家心肺血液研究所）的Framingham心脏研究专项数据集的一个子集，4000多个样本。

      

自变量分别为性别（sex）、收缩压（sbp）、舒张压（dbp）、血清胆固醇（scl）、年龄（age）、身体质量指数（bmi）等，因变量为冠心病相关死亡事件（chdfate）。因变量必须是二元变量，随访时间内死亡为1，未死亡为0。

下面建立两个模型，来演示怎样画出DCA曲线。一个是简单模型，以血清胆固醇值为预测方法（predictor），死亡事件为结果（outcome）；另一个是复合模型，联合性别、年龄、BMI、血清胆固醇、收缩压、舒张压为预测方法，死亡事件为结果。

准备工作

//#library(DecisionCurve) # 注：DecisionCurve包已经不再维护，更名为rmda
library(rmda)
setwd('D:\\DCA')
Data<- read.csv('2.20.Framingham.csv',sep = ',')

DCA运算

simple<- decision_curve(chdfate~scl,data = Data, family = binomial(link ='logit'),
thresholds= seq(0,1, by = 0.01),
confidence.intervals =0.95,study.design = 'case-control',
population.prevalence = 0.3)

#decision_curve()函数中，family =binomial(link = ‘logit’)是使用logistic回归来拟合模型。threshold设置横坐标阈概率的范围，一般是0 ~ 1；但如果有某种具体情况，大家一致认为Pt达到某个值以上，比如40%，则必须采取干预措施，那么0.4以后的研究就没什么意义了，可以设为0 ~ 0.4。by是指每隔多少距离计算一个数据点。

# Study.design可设置研究类型，是cohort还是case-control，当研究类型为case-control时，还应加上患病率population.prevalance参数。
complex<- decision_curve(chdfate~scl+sbp+dbp+age+bmi+sex,data = Data,
family = binomial(link ='logit'), thresholds = seq(0,1, by = 0.01),
confidence.intervals= 0.95,study.design = 'case-control',
population.prevalence= 0.3)
# 基本和simple相同，就是那几个联合应用的变量之间用个+号连接起来。
List<- list(simple,complex)
#把刚才计算的simple和complex两个对象合成一个list，命名为List。

DCA曲线绘制

plot_decision_curve(List,curve.names= c('simple','complex'),
cost.benefit.axis =FALSE,col = c('red','blue'),
confidence.intervals =FALSE,standardize = FALSE)

#plot_decision_curve()函数的对象就是刚才的List，如果只画一根曲线，就不需要合成的那步，直接把List替换成simple或complex就好了。

# curve.names是出图时，图例上每条曲线的名字，书写顺序要跟上面合成list时一致。cost.benefit.axis是另外附加的一条横坐标轴，损失收益比，默认值是TRUE，所在不需要时要记得设为FALSE。col就是颜色。confidence.intervals设置是否画出曲线的置信区间，standardize设置是否对净受益率（NB）使用患病率进行校正。

好了，这样就得到如下曲线：

      

可见，在Pt约为0.1~0.5范围内，复合评价模型的净受益率都比简单模型高。

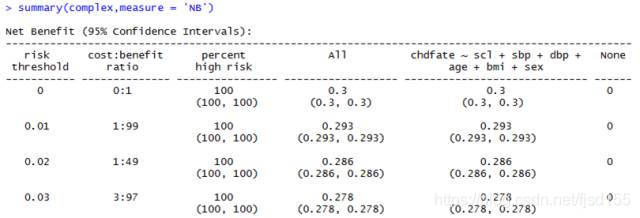
然后可用summary(complex,measure= 'NB')查看complex模型曲线上的各数据点，当然，NB也可以改成sNB，表示经过患病率的标准化：

      

接下来的一个函数，就是Kerr等人对DCA算法的进一步发展了，即绘制临床影响曲线（Clinical Impact Curve）：

plot_clinical_impact(simple,population.size = 1000,cost.benefit.axis = T,
      n.cost.benefits= 8,col = c('red','blue'),
      confidence.intervals= T)

# 使用simple模型预测1000人的风险分层，显示“损失:受益”坐标轴，赋以8个刻度，显示置信区间，得到下图：

      

红色曲线（Numberhigh risk）表示，在各个阈概率下，被simple模型划分为阳性（高风险）的人数；蓝色曲线（Number high risk with outcome）为各个阈概率下真阳性的人数。意义一目了然吧。

 

DCA算法的设计原理

其实了解到上面的也够了，再了解下面的就锦上添花啦~

它相当于在回归预测分析的基础上，引入了损失函数。先简单定义几个概念：

P：给真阳性患者施加干预的受益值（比如用某生化指标预测某患者有癌症，实际也有，予活检，达到了确诊的目的）；

L：给假阳性患者施加干预的损失值（比如预测有癌症，给做了活检，原来只是个增生，白白受了一刀）；

Pi：患者i有癌症的概率，当Pi > Pt时为阳性，给予干预。

所以较为合理的干预的时机是，当且仅当Pi × P >(1 – Pi) × L，即预期的受益高于预期的损失。推导一下可得，Pi > L / ( P + L )即为合理的干预时机，于是把L / ( P + L )定义为Pi的阈值，即Pt。

但对二元的预测指标来说，如果结果是阳性，则强制Pi=1，阴性则Pi = 0。这样，二元和其他类型的指标就有了可比性。

然后我们还可用这些参数来定义真阳性（A）、假阳性（B）、假阴性（C）、真阴性（D），即：

A：Pi ≥ Pt，实际患病；

B：Pi ≥ Pt，实际不患病；

C：Pi < Pt，实际患病；

D：Pi < Pt，实际不患病。

我们有一个随机抽样的样本，A、B、C、D分别为这四类个体在样本中的比例，则A+B+C+D = 1。那么，患病率（π）就是A + C了。

在这个样本中，如果所有Pi ≥ Pt 的人我们都给做了活检，那么就会有人确诊，有人白白被拉了一刀，那么净受益率NB = A × P – B × L。

但Vickers认为，知道P和L的确切值并没有什么实际意义，人们可能更关心L/P的比值，所以将上面的公式强行除以P，变成NB = A – B × L/P。根据Pt定义公式可推导出：NB = A – B × Pt / ( 1 – Pt )。以Pt为横坐标，U为纵坐标，画出来的曲线就是决策曲线。

若使用患病率进行校正，则U = A ×π– B ×(1 –π) × Pt / ( 1 – Pt )。

那么两个极端情况的曲线也很好推导了。当所有样本都是阴性（Pi < Pt），所有人都没干预，那么A = B = 0，所以NB = 0。当所有样本都是阳性，所有人都接受干预，那么C = D = 0，A = π，B = 1 –π（因为A+B+C+D=1），则NB = π– ( 1 –π )Pt / ( 1 – Pt )，所以它斜率为负值（

当然实际上，由这个表达式可知，阳性极端线不是直线，而是曲线）。

 

以上是分类模型中的决策曲线。生存模型也是有决策曲线的，具体请参考：mskcc/decision-curve-analysis

 

参考资料：

1.Decision curve analysis: anovel method for evaluating prediction models

2.Decision curve analysisrevisited: overall net benefit, relationships to ROC curve analysis, andapplication to case-control studies

3.Assessing the Clinical Impactof Risk Prediction Models With Decision Curves: Guidance for CorrectInterpretation and Appropriate Use