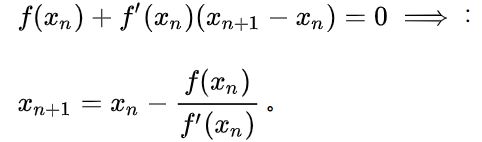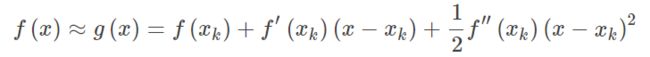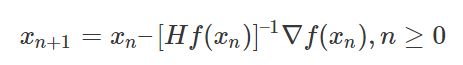机器学习-牛顿迭代法原理和公式推导

 

       机器学习的本质是建立优化模型，通过优化方法，不断迭代参数向量，找到使目标函数最优的参数向量，最终建立模型。但是在机器学习的参数优化过程中，很多函数是非常复杂的，不能直接求出。五次及以上多项式方程没有根式解，这个是被伽罗瓦用群论做出的最著名的结论，工作生活中还是有诸多类似求解高次方程的真实需求（比如行星的轨道计算，往往就是涉及到很复杂的高次方程）没有根式解不意味着方程解不出来，我们必须转向一些近似解法，通常用到的优化方法：梯度下降方法、牛顿法、拟牛顿法等，这些优化方法的本质就是在更新参数。

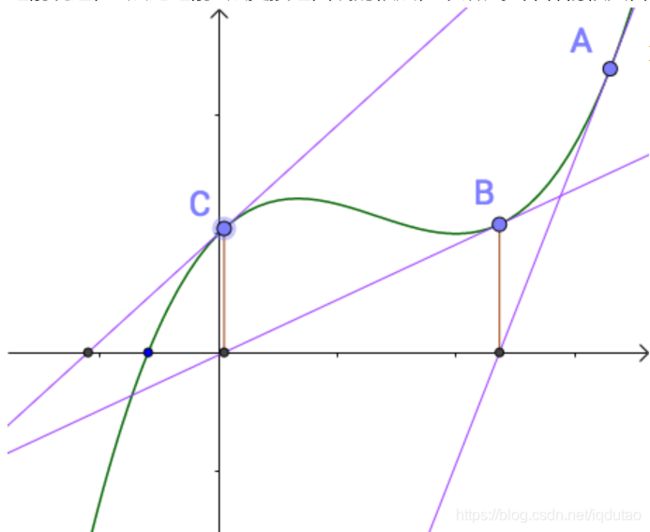
       牛顿迭代法又称为牛顿-拉弗森方法，实际上是由牛顿、拉弗森各自独立提出来的。牛顿-拉弗森方法提出来的思路就是利用切线是曲线的线性逼近这个思想，如下图所示：

                               

随便找一个曲线上的A点（为什么随便找，根据切线是切点附近的曲线的近似，应该在根点附近找，但是很显然我们现在还不知道根点在哪里），做一个切线，切线的根（就是和x轴的交点）与曲线的根，还有一定的距离。牛顿、拉弗森们想，没关系，我们从这个切线的根出发，做一根垂线，和曲线相交于B点，继续重复刚才的工作：

                                

之前说过，B点比之前A点更接近曲线的根点，牛顿、拉弗森们很兴奋，继续重复刚才的工作：

                               

第四次就已经很接近曲线的根了：

                              

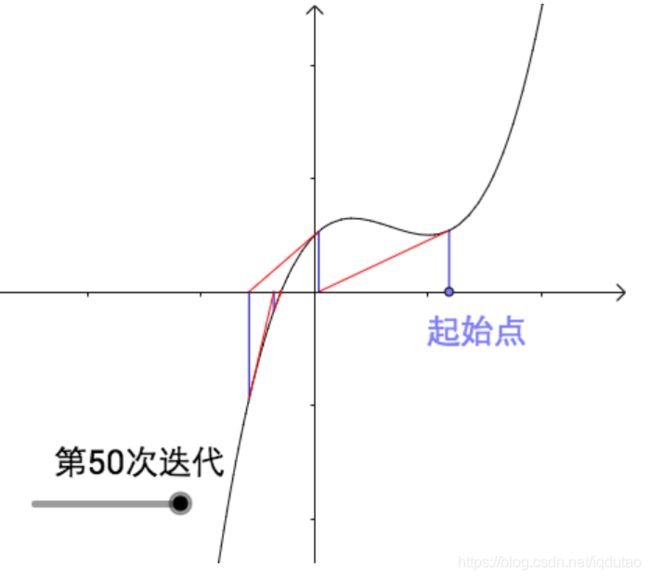
经过多次迭代后会越来越接近曲线的根（下图进行了50次迭代，哪怕经过无数次迭代也只会更接近曲线的根，用数学术语来说就是，迭代收敛了）：

                             

 

牛顿-拉弗森方法的代数解法

                                   

容易得出，点的切线方程为，要求，即相当于求的解，即

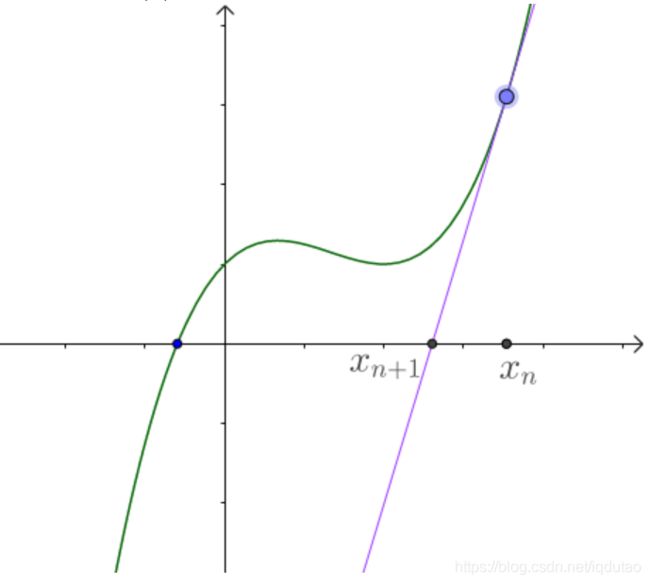
迭代过程可参考下图：

                      

 

        牛顿迭代法是用数值的方法来求解非线性方程组的根或其极大极小值，基本思想是：对于非线性函数f(x)，根据泰勒公式得到x附近某个点展开的多项式可用来近似函数f(x)的值，该多项式对应的函数为F(x)，求得F(x)的极小值作为新的迭代点，然后继续在新的迭代点泰勒公式展开，直到求得的极小值满足一定的精度。

假设函数f(x)二次可微，则二次泰勒展开，

                      

g(x)多项式则为f(x)的近似，求函数f(x)极值则可以转化为求导函数为0，对g(x)求导并令其为0，

                                             

得到，

                                                 

即得到迭代公式，

                                                

新的点不断逼近极值，直到一次导数小于某误差。代码中实现的核心的代码是x = (x + n/x)/2

                             

在上面讨论的是2维情况，高维情况的牛顿迭代公式是：

                                 

高维情况依然可以用牛顿迭代求解，但是问题是Hessian矩阵引入的复杂性，使得牛顿迭代求解的难度大大增加，但是已经有了解决这个问题的办法就是Quasi-Newton method，不再直接计算hessian矩阵，而是每一步的时候使用梯度向量更新hessian矩阵的近似。

        Hessian矩阵是一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率。牛顿法是迭代算法，每一步需要求解目标函数的Hessian矩阵的逆矩阵，计算过程复杂。拟牛顿法通过正定矩阵近似Hessian矩阵的逆矩阵或Hessian矩阵，简化计算过程。在数学中, 海森矩阵(Hessian matrix或Hessian)是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵, 此函数如下：

                                 

如果f的所有二阶导数都存在, 那么ff的海森矩阵即：

                                

(也有人把海森定义为以上矩阵的行列式)海森矩阵被应用于牛顿法解决的大规模优化问题。

 

梯度下降和牛顿法对比

      梯度下降每次只从你当前所处位置选一个坡度最大的方向走一步；牛顿法在选方向时，不仅会考虑坡度是否够大，还会考虑你走了一步后，坡度是否会变得更大，所以说牛顿法比梯度下降法看的更远一些，能更快地走到最底部。

牛顿法：是通过求解目标函数的一阶导数为0时的参数，进而求出目标函数最小值时的参数。另外牛顿法收敛速度很快。海森矩阵的逆在迭代过程中不断减小，可以起到逐步减小步长的效果。缺点：海森矩阵的逆计算复杂，代价比较大，因此有了拟牛顿法。

梯度下降法：是通过梯度方向和步长，直接求解目标函数的最小值时的参数。越接近最优值时，步长应该不断减小，否则会在最优值附近来回震荡

• 梯度下降法是一阶优化算法，牛顿法是二阶优化算法；
• 牛顿法的收敛速度相比梯度下降法常常较快；
• 牛顿法每次需要更新一个二维矩阵，计算代价很大，实际使用中常使用拟牛顿法；
• 牛顿法对初始值有一定要求，在非凸优化问题中（如神经网络训练），牛顿法很容易陷入鞍点（牛顿法步长会越来越小），而梯度下降法则很容易逃离鞍点（因此在神经网络训练中一般使用梯度下降法，高维空间的神经网络中存在大量鞍点）；
• 梯度下降法在靠近最优点时会震荡，因此步长调整在梯度下降法中是必要的；

 

拟牛顿法

        牛顿法（Newton method）和拟牛顿法（quasi Newton method）是求解无约束最优化问题的常用方法，有收敛速度快的优点。牛顿法是迭代算法，每一步都需求解目标函数的海塞矩阵（Hessian Matrix），计算比较复杂。拟牛顿法通过正定矩阵近似海塞矩阵的逆矩阵或海塞矩阵，简化了这一计算过程。

　   拟牛顿法是求解非线性优化问题最有效的方法之一，于20世纪50年代由美国Argonne国家实验室的物理学家W.C.Davidon所提出来。Davidon设计的这种算法在当时看来是非线性优化领域最具创造性的发明之一。不久R. Fletcher和M. J. D. Powell证实了这种新的算法远比其他方法快速和可靠，使得非线性优化这门学科在一夜之间突飞猛进。

　　拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷，它使用正定矩阵来近似Hessian矩阵的逆，从而简化了运算的复杂度(类似于弦截法，导数需要近似)；而且有时候目标函数的H矩阵无法保证正定。拟牛顿法和最速下降法一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化，构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法，尤其对于困难的问题。另外，因为拟牛顿法不需要二阶导数的信息，所以有时比牛顿法更为有效。如今，优化软件中包含了大量的拟牛顿算法用来解决无约束，约束，和大规模的优化问题。

 

       拟牛顿法的基本思想是：不用求二阶偏导数而构造出可以近似海赛矩阵（或海赛矩阵的逆）的正定对称阵。不同的构造方法对应能够产生不同的拟牛顿法。（可以理解成，"拟牛顿法"是来近似"牛顿法"的，所以在“牛顿法”前面加了一个“拟”字。拟牛顿法可不止一种，它包含多种方法：如DFP算法、BFGS算法、Broyden类算法。）

 

 

参考：https://blog.csdn.net/wangyangzhizhou/article/details/78547539
参考：https://zhuanlan.zhihu.com/p/77497823
参考：https://www.matongxue.com/madocs/205.html
参考：https://blog.csdn.net/pipisorry/article/details/24574293