Day03-《西瓜书》-决策树(DataWhale)

四、决策树

(decision tree)

4.1 基本流程

决策树

• 是通过一系列规则对数据进行分类的过程。
• 决策树表示给定特征条件下类的条件概率分布

决策树组成：

• 内部结点(internal node)：表示一个特征或属性
• 叶结点(leaf node)：一个类别或某个值

决策树生成步骤：

• 特征选择
• 决策树生成
• 决策树的修剪

4.2 决策树算法

4.2.1 基础知识

信息熵

自信息：
$$I(X)=-lo{g}_{b}p(x)$$
熵的理论解释：

（1）信息熵(自信息的期望)

X是一个取有限个解的离散随机变量，概率分布为：
$$P(X=x_i)=p_i,(i=1,2,...,n)$$
随机变量X的熵定义为：
$$H(X)=-\sum _{i=1}^n{p}_{i}log{p}_i$$
$log$取$lo{g}_2$时，熵的单位为比特(bit)

$log$取$lo{g}_e$时，熵的单位为纳特(nat)

熵只依赖于X的分布，与X无关，则：
$$H(p)=-\sum _{i=1}^n{p}_{i}log{p}_i$$
熵越大，随机变量的不确定性越大：$n\le H(p)\le lo{g}_n$。

约定：若$p(x)=0$，则$p_{i}log{p}_i=0$，当X的某个取值的概率为1时信息熵最小(最确定)；当X的各个取值的概率均等时信息熵最大(最不确定)，其值为$log|X|,|X|$表示X取值的个数

举例：

当X服从0~1分布：$P(X=1)=p;P(X=0)=1-p$

熵为：$H(p)=-plo{g}_{2}p-(1-p)lo{g}_2(1-p)$

（2）条件熵

联合概率分布为：$P(X=x_i,Y=y_j)=p_{ij}，i=1,2,...,n;j=1,2,3,...,m$

条件熵$H(Y|X)$：表示在已知随机变量X的条件下随机变量Y的不确定性，定义为X给定条件下Y的条件概率分布的熵对X的数学期望：
$$H(Y|X)=\sum _{i=1}^n{p}_{i}H(Y|X=x_i)$$
【当熵和条件熵中的概率由数据估计，特别是极大似然估计，得到所对应的熵与条件熵分别称为经验熵(empirical entropy) 和经验条件熵(empirical conditional entropy)】

信息增益

信息增益：特征A对训练数据集D的信息增益，g(D,A)定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差：
$$g(D,A)=H(D)-H(D|A)$$

• 互信息(mutual information)：表示得知特征X的信息而使得类Y的信息的不确定性减少的程度
• 机器学习中的信息增益等价于训练数据集中类与特征的互信息
• 信息增益越大，意味着使用该属性来进行划分所获得的==“纯度提升越大”==

算法：

设训练数据集为D，|D| 表示样本数量，

设有K个类$C_k,k=1,2,...,K$，|$C_k$|为所属类$C_k$的样本个数

特征A有n个不同的取值$\{a_1,a_2,...a_n\}$

根据A的取值将D划分为n个子集$\{D_1,,D_2,...,D_n\}$。|$D_i$|为$D_i$的样本数量

子集$D_i$中属于类$C_k$的样本集合为$D_{ik}$，|$D_{ik}$|为$D_{ik}$的样本个数

• 输入：训练集D 和特征A

  • 计算D的经验熵H(D)
    $$Ent(D)=H(D)=-\sum _{k=1}^K\frac{|C_k|}{|D|}lo{g}_2\frac{|C_k|}{|D|}$$

  • 计算特征A对D的经验条件熵H(D|A)
    $$H(D|A)=\sum _{i=1}^n\frac{|D_i|}{|D|}H(D_i)$$

  • 计算信息增益
    $$Gain(D,A)=g(D,A)=H(D)-H(D|A)$$

流程：

• 决定分类属性
• 建立一个结点N
• 如果数据都属于同一类，N就是树叶，在树叶上标出所属的类；如果没有其他属性可以考虑，N也是树叶，按照少数服从多数的原则标出所属的类别
• 否则，根据条件熵或信息增益选择最佳属性作为结点N的测试属性
• 结点属性选定后，对于该属性中的每一个值建立子树

信息增益比(增益率)

修正信息增益偏向于选择取值较多的特征的问题

定义：信息增益与训练数据集D关于特征A的值的熵之比
$$g_R(D,A)=\frac{g(D,A)}{H_A(D)}$$
其中，
$$H_A(D)=-\sum _{i=1}^n\frac{|D_i|}{|D|}lo{g}_2\frac{|D_i|}{|D|}$$

4.2.2 CLS算法

Concept Learning System

基本思想：

• 从一棵空决策树开始，选择某一属性作为测试属性，根据该属性值的不同，将训练样本分成对应的子集
  • 如果子集为空，或子集中的样本属于同一类，则选择该子集作为叶结点
  • 否则该子集对应于决策树的内部结点，需要选择一个新的分类属性对该子集进行划分，直到所有的子集都为空或属于同一类

缺点：

根据某种策略从训练样本属性表中选择属性A作为测试属性。没有规定采用何种测试属性。实践表明，测试属性集的组成以及测试属性的先后对决策树的学习具有举足轻重的影响

4.2.3 ID3算法

• 主要针对属性选择问题
• 使用信息增益度选择测试属性
• 在获取信息时，将不确定的内容转为确定的内容

基本思想

以信息熵为度量，用于决策树结点的属性选择，每次优先选取信息量最多的属性(熵值变为最小的属性)，以构造一个熵值下降最快的决策树，到叶子结点处的熵值为0。此时，每个叶子结点对应的实例集中的实例属于同一类。

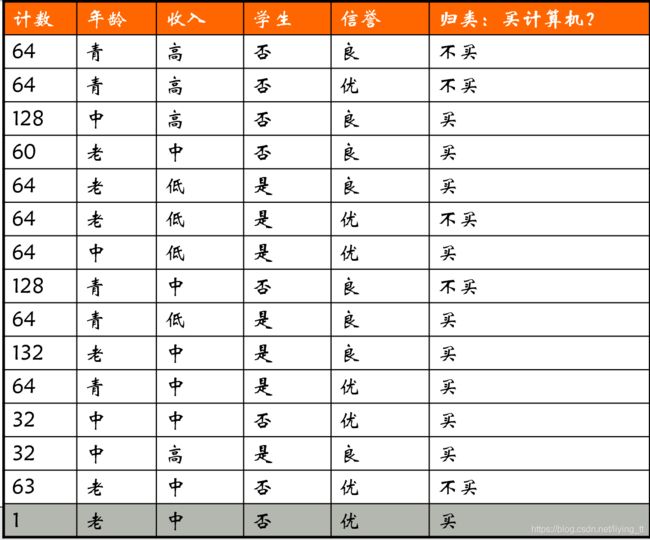
案例

第一步：计算决策属性的熵：

决策属性：“买计算机？”；该属性分两类：(买,不买)

$|C_1|(买)$=128+60+64+64+64+132+64+32+32+1=641

$|C_2|(不买)$=64+64+64+128+63=383

$|D|=|C_1|+|C_2|=1024$

$P_1=\frac{|C_1|}{D}=\frac{641}{1024}=0.626$

$P_2=0.374$

$H(D)=-P_{1}lo{g}_2{P}_1-P_{2}lo{g}_2{P}_2=0.9537$

第二步：计算条件属性的熵：

条件属性(4个)：年龄、收入、学生、信誉

1）计算年龄的信息增益

年龄分为：青、中、老

• 青年

$|D_{11}|(买)$=64+64=128

$|D_{12}|(不买)$=64+64+128=256

$|D_1|$=128+256=284

$P_1=\frac{128}{384}$=0.333

$P_2=\frac{256}{384}$=0.667

$H(D_1)=-P_{1}lo{g}_2{P}_1-P_{2}lo{g}_2{P}_2=0.9183$

• 中年

中年全部是买

$H(D_2)=-P_{1}lo{g}_2{P}_1-P_{2}lo{g}_2{P}_2=0$

• 老年

$H(D_3)=-P_{1}lo{g}_2{P}_1-P_{2}lo{g}_2{P}_2=0.9157$

计算信息增益

$\frac{|D_i|}{|D|}$

青年：$\frac{384}{1024}=0.375$

中年：$\frac{256}{1024}=0.25$

老年：$\frac{384}{1024}=0.375$

$H(D|年龄)=0.375\ast 0.9183+0.25\ast 0+0.375\ast 0.9157=0.6877$

$g(D|年龄)=H(D)-H(D|年龄)=0.9537-0.6877=0.266$

同理：

$H(D|收入)=0.9361$

$g(D|收入)=H(D)-H(D|收入)=0.0176$

$H(D|学生)=0.7811$

$g(D|学生)=H(D)-H(D|学生)=0.1726$

$H(D|信誉)=0.9048$

$g(D|信誉)=H(D)-H(D|信誉)=0.0453$

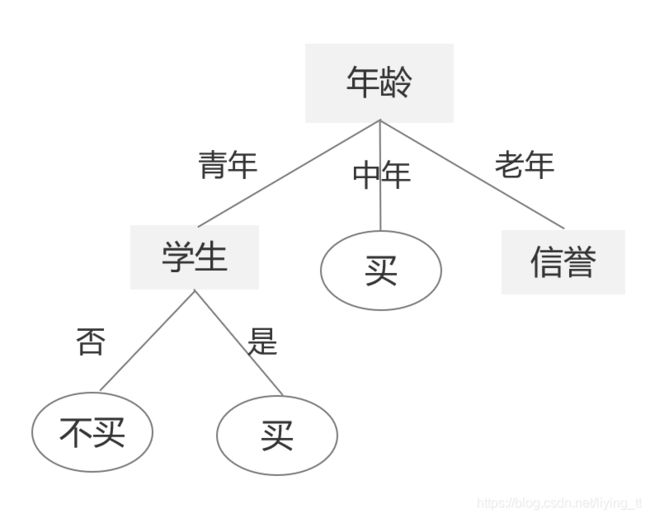
比较上面四种属性的信息增益，选择信息增益最大的作为结点，因此选择年龄

第三步：继续选择结点

1) 青年之后选择收入作为结点，分为高、中、低

$|C_1|(买)$=128

$|C_2|(不买)$=256

$|D|$=384

$|P_1|$ = 0.333

$|P_2|$ = 0.667

$H(D)=-P_{1}lo{g}_2{P}_1-P_{2}lo{g}_2{P}_2=0.9183$

收入高：

$|D_{11}|(买)$=0

$|D_{12}|(不买)$=128

$|D_1|$=128

$P_1=\frac{0}{128}$=0

$P_2=\frac{128}{128}$=1

$H(D_1)=-P_{1}lo{g}_2{P}_1-P_{2}lo{g}_2{P}_2=0$

比例：$\frac{128}{384}=0.333$

同理：

收入中：$H(D_2)=0.9183$

收入中比例：0.5

收入低：$H(D_3)=0$

收入低比例：0.167

$H(年龄|收入)=0.333\ast 0+0.5\ast 0.9183+0\ast 0.167=0.4592$

$g(年龄|收入)=H(D)[青年]-H(年龄|收入)=0.9183-0.4592=0.4591$

2) 青年之后选择学生作为结点，分为是、否

是学生：

$|D_{11}|(买)$=128

$|D_{12}|(不买)$=0

$|D_1|$=128

$P_1=\frac{128}{128}$=1

$P_2=\frac{0}{128}$=0

$H(D_1)=-P_{1}lo{g}_2{P}_1-P_{2}lo{g}_2{P}_2=0$

比例：$\frac{128}{384}=0.333$

同理：

不是学生：$H(D_2)=0$

不是学生：0.667

$H(年龄|学生)=0.333\ast 0+0.667\ast 0=0$

$g(年龄|学生)=H(D)[青年]-H(年龄|学生)=0.9183-0=0.9183$

3) 青年之后选择信誉作为结点，分为良、优

信誉良：

$|D_{11}|(买)$=64

$|D_{12}|(不买)$=192

$|D_1|$=256

$P_1=\frac{64}{256}$=0.25

$P_2=\frac{192}{256}$=0.75

$H(D_1)=-P_{1}lo{g}_2{P}_1-P_{2}lo{g}_2{P}_2=0.8113$

比例：$\frac{256}{384}=0.667$

同理：

信誉优：$H(D_2)=1$

信誉优比例：0.333

$H(年龄|信誉)=0.667\ast 0.8113+0.333\ast 1=0.8741$

$g(年龄|信誉)=H(D)[青年]-H(年龄|学生)=0.9183-0.8741=0.0442$

通过比较信息增益，青年之后选择学生属性继续划分，熵值为0即可暂停

决策树：

不足

• 连续特征问题
• 信息增益作为标准容易偏向取值较多的特征
• 缺失值问题
• 过拟合问题

4.2.4 C4.5算法

来源：https://www.cnblogs.com/keye/p/10267473.html

优化ID3的四个问题：

1. 对不能处理连续值特征

将连续的特征离散化

• 将m个连续样本从小到大排序
• 取相邻两个样本值得平均数，得到m-1个划分点
• 对m-1个划分点，分别计算以该点作为二元分类点时得信息增益。选择信息增益最大点作为该连续特征的二元离散分类点（比如取到的增益最大的点为$a_t$，则小于$a_t$的值为类别1，大于$a_t$的值为类别2，这样就做到了连续特征的离散化。注意的是，与离散属性不同，如果当前节点为连续属性，则该属性后面还可以参与子节点的产生选择过程）
• 用信息增益比选择最佳划分

2. 对信息增益容易偏取值较多特征的问题

选择信息增益比作为标准

3. 对于缺失值处理的问题

1. 样本某些特征缺失情况下选择划分的属性

​ 对于有缺失特征值的特征属性A，对每一个样本设置一个权重(初始值为1)，然后划分数据，一部分是由特征值A的数据$D_1$，另一部分是没有特征A的数据$D_2$，然后对于没有缺失特征A的数据集$D_1$来和对应的A特征的每个特征值一起计算加权重后的信息增益比，最后乘上特征A缺失的样本加权后所占加权总样本的比例。

2. 选定了划分属性，对于在该属性上缺失特征的样本的处理

​ 将缺失特征的样本同时划分入所有的子节点，该样本的权重按各个结点样本的数量比例来分配。

​ 例如：缺失特征A的样本a之前权重为1，特征A有3个特征值$A_1,A_2,A_3$。3个特征值对应的无缺失A特征的样本个数为2，3，4。则a同时划分入$A_1,A_2,A_3$对应权重调整为$(\frac{2}{9},\frac{3}{9},\frac{4}{9})$

不足与改进：

• 非常容易过拟合。需要进行剪枝
• 生成的是多叉树，效率不如二叉树
• 只能用于分类
• 使用了熵模型，有大量对数计算，运算强度高。可以用基尼系数代替熵模型

4.2.5 CART算法

来源：https://www.cnblogs.com/keye/p/10564914.html

使用基尼系数代替信息增益比。

基尼系数

• 代表了模型的不纯度
• 基尼系数越小，不纯度越低，特征越好。【与信息增益（比）相反】

价格K个类别，第k个类别的概率为$P_k$，概率分布的基尼系数表达式：
$$Gini(P)=\sum _{k=1}^K{P}_k(1-P_k)=1-\sum _{k=1}^K{P}_k^2$$
二分类问题，第一个样本输出概率为p，则概率分布的基尼系数为：
$$Gini(P)=2p(1-p)$$
对于样本D，个数|D|，类别为K，第k个类别的数量为$|C_k|$，则样本D的基尼系数为：
$$Gini(D)=1-\sum _{k=1}^K(\frac{|C_k|}{|D|}{)}^2$$
对于样本D，个数|D|，根据特征A将D划分为n类，则在特征A的条件下，样本D的基尼系数表达式为：
$$Gini(D,A)=\sum _{i=1}^n\frac{|D_i|}{|D|}Gini(D_i)$$
CART分类树算法每次仅对某一特征的值进行二分，不进行多分，可以建立二叉树

案例

1) 计算各特征的基尼系数

$|D|$=15

$(A_1,A_2,A_3,A_4)$代表(年龄, 收入, 学生, 信誉)

$A_1$取值(1, 2 ,3)代表(青，中，老)

$A_2$取值(1, 2, 3)代表(低，中，高)

$A_3$取值(1, 2)代表(是，否)

$A_4$取值(1, 2)代表(良，优)

$Gini(D,A_1=1)=\frac{5}{15}\ast (2\times \frac{2}{5}\times (1-\frac{2}{5}))+\frac{10}{15}\ast (2\times \frac{8}{10}\times (1-\frac{8}{10}))=0.3733$

$Gini(D,A_1=2)=\frac{4}{15}\ast (2\times \frac{4}{4}\times (1-\frac{4}{4}))+\frac{11}{15}\ast (2\times \frac{6}{11}\times (1-\frac{6}{11}))=0.3636$

$Gini(D,A_1=3)=\frac{6}{15}\ast (2\times \frac{4}{6}\times (1-\frac{4}{6}))+\frac{9}{15}\ast (2\times \frac{6}{9}\times (1-\frac{6}{9}))=0.4444$

基尼系数最小的为$A_1$=2，所以$A_1=2$是$A_1$的最优切分点

求$A_2$的基尼系数：

$Gini(D,A_2=1)=\frac{4}{15}\ast (2\times \frac{3}{4}\times (1-\frac{3}{4}))+\frac{11}{15}\ast (2\times \frac{7}{11}\times (1-\frac{7}{11}))=0.4394$

$Gini(D,A_2=2)=\frac{6}{15}\ast (2\times \frac{4}{6}\times (1-\frac{4}{6}))+\frac{9}{15}\ast (2\times \frac{6}{9}\times (1-\frac{6}{9}))=0.4444$

$Gini(D,A_2=3)=\frac{4}{15}\ast (2\times \frac{2}{4}\times (1-\frac{2}{4}))+\frac{11}{15}\ast (2\times \frac{8}{11}\times (1-\frac{8}{11}))=0.4242$

基尼系数最小的为$A_2$=3，所以$A_2=3$是$A_2$的最优切分点

求$A_3$的基尼系数

$Gini(D,A_3=1)=\frac{7}{15}\ast (2\times \frac{6}{7}\times (1-\frac{6}{7}))+\frac{8}{15}\ast (2\times \frac{5}{8}\times (1-\frac{4}{8}))=0.381$

【$A_3$只有两类，所以$A_3=1$和$A_3=2$结果一致】

求$A_4$的基尼系数

$Gini(D,A_4=1)=\frac{8}{15}\ast (2\times \frac{6}{8}\times (1-\frac{6}{8}))+\frac{7}{15}\ast (2\times \frac{4}{7}\times (1-\frac{4}{7}))=0.4286$

在($A_1,A_2,A_3,A_4$)中，$Gini(D,A_1=2)$最小，所以A_1为最优特征，$A_1=2$为其最优切分点

年龄根结点生成一个叶结点【是中年属性为：买】，一个内部结点【不是中年】，然后再使用上述方法，在不是中年的样本中继续进行基尼系数计算，选择出最优特征及最优切分点