区间子数组个数
@author: sdubrz
@date: 2020.03.26
题目难度: 中等
原题链接 https://leetcode-cn.com/problems/number-of-subarrays-with-bounded-maximum/
题目的著作权归领扣网络所有,商业转载请联系官方授权,非商业转载请注明出处。
解题代码转载请联系 lwyz521604#163.com
给定一个元素都是正整数的数组A ,正整数 L 以及 R (L <= R)。
求连续、非空且其中最大元素满足大于等于L 小于等于R的子数组个数。
例如 :
输入:
A = [2, 1, 4, 3]
L = 2
R = 3
输出: 3
解释: 满足条件的子数组: [2], [2, 1], [3].
注意:
- L, R 和 A[i] 都是整数,范围在 [0, 10^9]。
- 数组 A 的长度范围在[1, 50000]。
我的解法
给定L和R,A中的数可以分为三类:
- 大于R的数。这种数一定不在符合要求的子数组中。
- 大于等于L并且小于等于R的数。每个符合要求的子数组中必然至少含有一个这种数。
- 小于L的数。对于每个子数组来讲,这种数可有可无。
我先根据大于R的数,把数组A划分成了几个连续的区域,相邻区域之间以一个大于R的元素为界。这样,我们可以分别求每个区域有多少个满足要求的子数组,最后对它们求和,就是整个A中满足要求的子数组个数。这样,原问题就转化为了求每个区域中符合要求的子数组的个数。
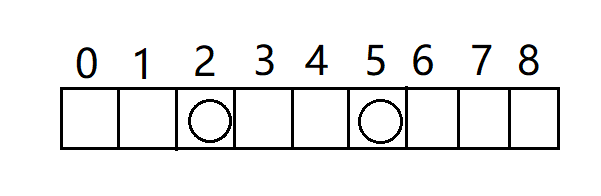
划分所得的每个区域中,只包含第二类点和第三类点。其中,每个符合要求的子数组中必然至少包含一个第二类点。下图是一个我们划分所得的一个区域,其中圆圈所示的位置为第二类点,其他位置为第三类点。
计算每个区域中符号要求的子数组个数,可以用这样的方法:每次选取一个第二类点,作为子数组必须包含的元素,然后截取出从上一个第二类点的后面一个元素到该区域末尾这段区间。计算这个区间在必须包含选中的这个第二类点的情况下,有多少个符合条件的子数组。记在该区间中,选中的第二类点的左边有n_left个元素,右边有n_right个点,要计算的子数组数为 n_left + n_right + n_left*n_right + 1
比如上图中共有2个第二类点,其中,第一个二类点是第2个元素,它所对应的区间为0到8,也就是整个区域。在该区间上,必须包含该元素的子数组个数为2+6+2*6+1=21
第二个第二类点(第5个元素)。它所对应的区间是从第3个元素到第8个元素。则该区间上,包含第5个元素的子数组个数为 2+3+2*3+1=12
所以整个区域上符合要求的子数组个数为21+12=33
按照上述思想,整个问题的Java实现如下。
import java.util.*;
class Solution {
public int numSubarrayBoundedMax(int[] A, int L, int R) {
int count = 0;
int left = 0;
int right = -1;
ArrayList list = new ArrayList<>();
for(int i=0; i=L) {
list.add(i);
}
count = count + this.subArray(left, right, list);
}
if(A[i] > R) {
right = i - 1;
count = count + this.subArray(left, right, list);
list = new ArrayList<>();
left = i + 1;
}else {
if(A[i]>=L) {
list.add(i);
}
right++;
}
}
return count;
}
public int subArray(int left, int right, ArrayList list) {
if(left>right) {
return 0;
}
if(list.isEmpty()) { // 如果这个子数组段中所有的元素都小于L
return 0;
}
int count = 0;
int last = left - 1;
for(int i=0; i 这段程序在系统中提交的结果为
执行结果:通过
执行用时 : 7 ms, 在所有 Java 提交中击败了 38.24% 的用户
内存消耗 : 41.6 MB, 在所有 Java 提交中击败了 100.00% 的用户
可以看到这个方法的空间复杂度还不错,但是时间上表现地不够优秀。
官方解法
下面是LeetCode官方账号给出的答案(链接:https://leetcode-cn.com/problems/number-of-subarrays-with-bounded-maximum/solution/qu-jian-zi-shu-zu-ge-shu-by-leetcode/)。
思想
根据以下步骤推导出解决方案:
其实我们只关心数组中的元素是否小于 L,大于 R,或者位于 [L, R] 之间。假设一个元素小于 L 标记为 0,位于 [L, R] 之间标记为 1,大于 R 标记为 2。
我们希望找出不包含 2 且至少包含一个 1 的子数组数量。因此可以看作是所有的 2 将数组拆分为仅包含 0 或 1 的子数组。例如在数组 [0, 0, 1, 2, 2, 1, 0, 2, 0],2 将数组拆分为 [0, 0, 1]、[1, 0] 和 [0] 三个子数组。
接下来,需要计算每个只包含 0 或 1 的数组中,至少包含一个 1 的子数组数量。那么问题可以转换为先找出所有的子数组,再从中减去只包含 0 的子数组。
例如,[0, 0, 1] 有 6 个子数组,其中 3 个子数组只包含 0,3 个子数组至少包含一个 1;[1, 0] 有 3 个子数组,其中 1 个子数组只包含 0,2 个子数组至少包含一个 1;[0] 只有 1 个子数组,且这个子数组只包含 0。因此数组 A = [0, 0, 1, 2, 2, 1, 0, 2, 0] 中不包含 2,且至少包含一个 1 的子数组的数量是 3 + 2 + 0 = 5。
算法
假设 count(B) 用于计算所有元素都小于等于 B 的子数组数量。根据上面分析,本题答案为 count® - count(L-1)。
那么如何计算 count(B)?使用 cur 记录在 B 的左边,小于等于 B 的连续元素数量。当找到一个这样的元素时,在此位置上结束的有效子数组的数量为 cur + 1。当遇到一个元素大于 B 时,则在此位置结束的有效子数组的数量为 0。
class Solution {
public int numSubarrayBoundedMax(int[] A, int L, int R) {
return count(A, R) - count(A, L-1);
}
public int count(int[] A, int bound) {
int ans = 0, cur = 0;
for (int x: A) {
cur = x <= bound ? cur + 1 : 0;
ans += cur;
}
return ans;
}
}
看着这么短的程序,真实不得不感叹……