Gurobi 安装到使用教程(2)
Gurobi 安装到使用教程(2)
- 1. 基本操作
- 2. 基本建模举例
1. 基本操作
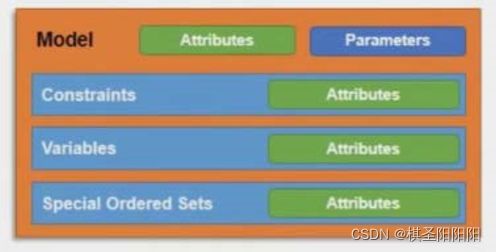
Gurobi的建模基本概念主要包括:参数(Parameter)和属性(Attributes)两种。前者控制优化器的行为,后者主要是控制模型的特性,包括(模型、变量、约束、目标等对象)。
Python的tuple,list,dictionary在gurobi中都可以使用,但是Gurobi推荐使用自己的Tuplelist和TupleDict,在循环和检索上运算速度更快。
- tuplelist
Cities= [('A','B'), ('A','C'), ('B','C'),('B','D'),('C','D')]
Routes = tuplelist(Cities)
# 使用tuplelist() 不能忘记from gurobipy import *
# tuplelist 增加了快速筛选 select 功能
print(Routes.select('A','*'))
Result=[]
for i,j in Cities:
if i=='A':
Result.append((i,j))
print(Result)
2) tupledict
Gurobi tupledict –Python Dictionary 扩展
键值为tuple (元组),可以使用 select, sum, prod 函数,用于变量和约束
3) Multidict() 创建 tuplelist 和tupledict 的便捷方法
cities, supply, demand = multidict({
'A': [100, 20],
'B': [150, 50],
'C': [20, 300],
'D': [10, 200]})
m = Model()
# 创建基本模型
m.addVar()
m.addVars()
# 先添加决策变量
m.setObjective()
# 确定目标函数
m.addConstr()
m.addConstrs()
# 添加约束
TupleList,select()
tupledict.prod()
# 乘法
GRB.LESS_EQUAL, GRB.EQUAL, or GRB.GREATER_EQUAL
# 约束的一些操作
2. 基本建模举例
import gurobipy as gp
from gurobipy import GRB
try:
# Create a new model
m = gp.Model("mip1")
# Create variables
x = m.addVar(vtype=GRB.BINARY, name="x")
y = m.addVar(vtype=GRB.BINARY, name="y")
z = m.addVar(vtype=GRB.BINARY, name="z")
# Set objective
m.setObjective(x + y + 2 * z, GRB.MAXIMIZE)
# Add constraint: x + 2 y + 3 z <= 4
m.addConstr(x + 2 * y + 3 * z <= 4, "c0")
# Add constraint: x + y >= 1
m.addConstr(x + y >= 1, "c1")
# Optimize model
m.optimize()
for v in m.getVars():
print('%s %g' % (v.VarName, v.X))
print('Obj: %g' % m.ObjVal)
except gp.GurobiError as e:
print('Error code ' + str(e.errno) + ': ' + str(e))
except AttributeError:
print('Encountered an attribute error')
- 营养配方模型
人体需要四种营养:category : calories, protein, fat, sodium
食物来源:foods= hamburger, chicken, hot dog, fries, macaroni, pizza, salad, milk, ice cream
营养吸收每天有上限和下限 单位重量食物价格不同 单位重量食物所含营养成分不同
求达到足够营养花费的代价最小
import gurobipy as gp
from gurobipy import GRB
# Nutrition guidelines, based on
# USDA Dietary Guidelines for Americans, 2005
# http://www.health.gov/DietaryGuidelines/dga2005/
categories, minNutrition, maxNutrition = gp.multidict({
'calories': [1800, 2200],
'protein': [91, GRB.INFINITY],
'fat': [0, 65],
'sodium': [0, 1779]})
foods, cost = gp.multidict({
'hamburger': 2.49,
'chicken': 2.89,
'hot dog': 1.50,
'fries': 1.89,
'macaroni': 2.09,
'pizza': 1.99,
'salad': 2.49,
'milk': 0.89,
'ice cream': 1.59})
# Nutrition values for the foods
nutritionValues = {
('hamburger', 'calories'): 410,
('hamburger', 'protein'): 24,
('hamburger', 'fat'): 26,
('hamburger', 'sodium'): 730,
('chicken', 'calories'): 420,
('chicken', 'protein'): 32,
('chicken', 'fat'): 10,
('chicken', 'sodium'): 1190,
('hot dog', 'calories'): 560,
('hot dog', 'protein'): 20,
('hot dog', 'fat'): 32,
('hot dog', 'sodium'): 1800,
('fries', 'calories'): 380,
('fries', 'protein'): 4,
('fries', 'fat'): 19,
('fries', 'sodium'): 270,
('macaroni', 'calories'): 320,
('macaroni', 'protein'): 12,
('macaroni', 'fat'): 10,
('macaroni', 'sodium'): 930,
('pizza', 'calories'): 320,
('pizza', 'protein'): 15,
('pizza', 'fat'): 12,
('pizza', 'sodium'): 820,
('salad', 'calories'): 320,
('salad', 'protein'): 31,
('salad', 'fat'): 12,
('salad', 'sodium'): 1230,
('milk', 'calories'): 100,
('milk', 'protein'): 8,
('milk', 'fat'): 2.5,
('milk', 'sodium'): 125,
('ice cream', 'calories'): 330,
('ice cream', 'protein'): 8,
('ice cream', 'fat'): 10,
('ice cream', 'sodium'): 180}
# Model
m = gp.Model("diet")
# Create decision variables for the foods to buy
buy = m.addVars(foods, name="buy")
# You could use Python looping constructs and m.addVar() to create
# these decision variables instead. The following would be equivalent
#
# buy = {}
# for f in foods:
# buy[f] = m.addVar(name=f)
# The objective is to minimize the costs
m.setObjective(buy.prod(cost), GRB.MINIMIZE)
# Using looping constructs, the preceding statement would be:
#
# m.setObjective(sum(buy[f]*cost[f] for f in foods), GRB.MINIMIZE)
# Nutrition constraints
m.addConstrs((gp.quicksum(nutritionValues[f, c] * buy[f] for f in foods)
== [minNutrition[c], maxNutrition[c]]
for c in categories), "_")
# Using looping constructs, the preceding statement would be:
#
# for c in categories:
# m.addRange(sum(nutritionValues[f, c] * buy[f] for f in foods),
# minNutrition[c], maxNutrition[c], c)
def printSolution():
if m.status == GRB.OPTIMAL:
print('\nCost: %g' % m.ObjVal)
print('\nBuy:')
for f in foods:
if buy[f].X > 0.0001:
print('%s %g' % (f, buy[f].X))
else:
print('No solution')
# Solve
m.optimize()
printSolution()
print('\nAdding constraint: at most 6 servings of dairy')
m.addConstr(buy.sum(['milk', 'ice cream']) <= 6, "limit_dairy")
# Solve
m.optimize()
printSolution()

