机器学习算法 - 从线性回归到前馈神经网络

1.机器学习算法简介

 在本文中，关注的是预测任务，包括使用一组观察情况来预测结果。着重于以下方面:

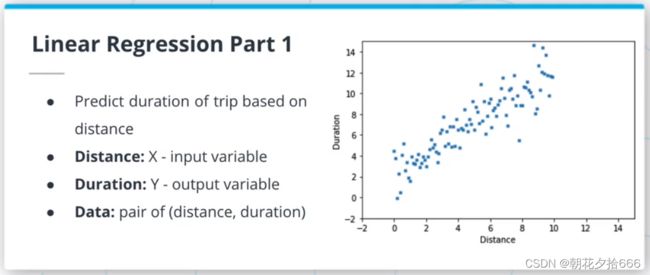
    Regression（回归）:预测一个量(如距离、时间)，理解两个变量之间的关系。
    Classification（分类）:为输入分配一个离散的类别(如交通标志)。

 本文主要内容如下:

    线性回归
    逻辑回归
    梯度下降法优化
    前馈神经网络
    反向传播
    基于神经网络的图像分类

2.概述

在本文中，将创建ML模型，根据输入来预测输出。为了估计模型的拟合度，使用一个损失函数，并使用选定的度量标准对所创建的模型的性能进行量化。

模型:从输入中提取模式的一组计算。
损失函数/成本函数:将模型输出映射到单个实数的函数。
度量/标准:对算法性能进行量化的函数。

3.线性回归 

线性回归模型是ML算法的一种，假定输入变量和输出变量之间是线性关系。该模型由两个参数描述:斜率m和交点b，使y = mx +b。拟合或训练这样的模型需要调整m和b，使所选择的损失函数最小化。

线性回归损失函数

均方误差(MSE)损失或L2损失是线性回归算法中最常用的函数之一。它是通过对真实值和预测值的平方差求和来计算的。由于平方函数的性质，这种损失对异常值(分布数据点之外)非常敏感。

如果数据集包含许多异常值，L1损失(真实值和预测值之间的绝对差异)可能是一个更好的候选值。

4.逻辑回归Logistic Regression

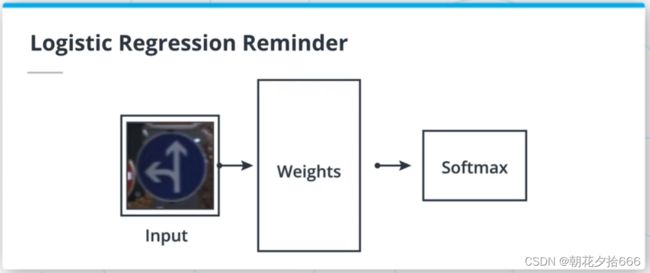
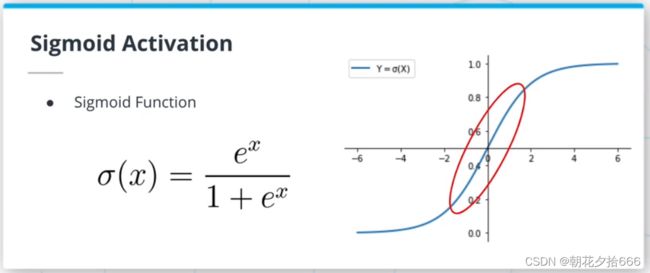
对于分类问题，也可以用一个线性表达式来建模一个输入属于某一分类的概率P(Y|X)。这样的模型被称为逻辑回归，看起来像这样:P(Y|X) = mx+b。然而，考虑到要建模一个概率，需要一种方法来限制mx+b的值在[0,1]区间内。为此，将使用logistic函数(或sigmoid)。logistic函数将任意实数映射到[0,1]区间。

softmax函数是logistic函数到多个类的扩展，并以矢量而不是实数作为输入。softmax函数输出一个离散的概率分布:相似维度的向量作为输入，但其所有分量之和为1。在本文的后面，将描述sigmoid和softmax函数作为激活函数。

交叉熵损失和One-Hot编码

交叉熵(CE)损失是分类问题中最常见的损失。总损失等于所有观测值之和，即真实值one-hot编码向量和softmax概率向量的对数的点积。

对于多类分类问题，真实值标签需要编码为向量进行计算。一种常见的方法是one-hot编码方法，其中数据集的每个标签都被分配一个整数。这个整数被用作one-hot向量中仅有的非零元素的索引。

小结:对于分类问题，标签需要编码为C维的向量，其中C为数据集中类的数量。由于softmax函数，该模型输出了一个离散的概率分布向量，同样是C维的。为了计算输入和输出之间的交叉熵损失，我们计算了一个one hot向量和输出的对数的点积。

5.Tensorflow简介

Tensorflow张量是与numpy数组共享许多属性和特征的数据结构(例如.shape和广播规则)。它们确实有额外的属性，允许用户将张量从一个设备移动到另一个设备(例如cpu到gpu)。

6.练习1 -逻辑回归
目的
在这个练习中，实现四个不同的功能:

Softmax:计算向量的Softmax值。这个函数以一个张量作为输入，输出一个离散的概率分布。

交叉熵(cross_entropy):给出一个预测向量(softmax后)，计算交叉熵损失和一个真实值向量(one-hot vector)。

模型:取一批图像(沿着第一个维度的图像堆栈)，输入到逻辑回归模型

准确度:给定一个预测向量和一个真实值向量，计算准确度。

运行python logic .py来检查你的实现。

提示
可以利用tf.boolean_mask函数来计算交叉熵。请记住，真实值向量的大多数元素都是零。
参考代码如下：

import tensorflow as tf

from utils import check_softmax, check_acc, check_model, check_ce


def softmax(logits):
    """
    softmax implementation
    args:
    - logits [tensor]: 1xN logits tensor
    returns:
    - soft_logits [tensor]: softmax of logits
    """
    exp = tf.exp(logits)
    denom = tf.math.reduce_sum(exp, 1, keepdims=True)
    return exp / denom


def cross_entropy(scaled_logits, one_hot):
    """
    Cross entropy loss implementation
    args:
    - scaled_logits [tensor]: NxC tensor where N batch size / C number of classes
    - one_hot [tensor]: one hot tensor
    returns:
    - loss [tensor]: cross entropy 
    """
    masked_logits = tf.boolean_mask(scaled_logits, one_hot) 
    return -tf.math.log(masked_logits)


def model(X, W, b):
    """
    logistic regression model
    args:
    - X [tensor]: input HxWx3
    - W [tensor]: weights
    - b [tensor]: bias
    returns:
    - output [tensor]
    """
    flatten_X = tf.reshape(X, (-1, W.shape[0]))
    return softmax(tf.matmul(flatten_X, W) + b)


def accuracy(y_hat, Y):
    """
    calculate accuracy
    args:
    - y_hat [tensor]: NxC tensor of models predictions
    - y [tensor]: N tensor of ground truth classes
    returns:
    - acc [tensor]: accuracy
    """
    # calculate argmax
    argmax = tf.cast(tf.argmax(y_hat, axis=1), Y.dtype)

    # calculate acc
    acc = tf.math.reduce_sum(tf.cast(argmax == Y, tf.int32)) / Y.shape[0]
    return acc


if __name__ == '__main__':
    # checking the softmax implementation
    check_softmax(softmax)

    # checking the NLL implementation
    check_ce(cross_entropy)

    # check the model implementation
    check_model(model)

    # check the accuracy implementation
    check_acc(accuracy)

7.梯度下降法（Gradient Descent）

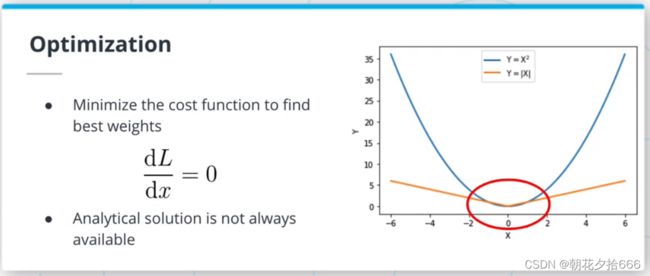
拟合或训练ML算法包括寻找使损失函数最小化的权重组合。 在某些情况下，可以找到解析方案(例如，L2损耗的线性回归：https://medium.com/m/global-identity?redirectUrl=https%3A%2F%2Ftowardsdatascience.com%2Fanalytical-solution-of-linear-regression-a0e870b038d5)。 然而，对于本文所处理的大多数算法而言，损耗最小化问题的解析解并不存在。

 

梯度下降算法是一种求损失函数最小值的迭代方法。 该算法使用由称为学习率（learning rate）的浮点数缩放的损失函数的梯度，向这个最小值迈进了一步。  
当使用梯度下降算法时，其中一个挑战是局部极小值的存在。 局部极小值是损失函数域的局部子集上的极小值。 它们是这个函数能取的最小值，只在这个小子集中，而不是全局最小值损失函数取整个域的最小值。 梯度下降算法可能会陷入局部极小值并输出次优解。 在本文的后面，我们将看到其他方法是如何解决这个问题的。
Tensorflow变量是具有固定类型和形状的张量，但其值可以通过操作来改变。 我们需要使用变量，采用tf.GradientTape api来计算Tensorflow中的梯度。

8.随机梯度下降法(SGD)

由于内存限制，整个数据集几乎不会一次加载并通过模型提供，就像批量梯度下降的情况一样。 相反，将创建批量输入。 一次只对一个输入的批次进行梯度下降称为随机梯度下降(SGD)，而多个批次但不是全部同时进行的(例如20批200张图片)称为小批量梯度下降。

9.练习2 -自定义训练循环
目的
在这个练习中，从头开始实现第一个训练和验证循环，以训练要实现的逻辑模型。为此，还必须创建一个优化器（Optimizers）。
细节
训练循环遍历训练数据集的元素，并使用它更新模型的权重。验证循环通过验证数据集的每个元素，并使用它来计算指标(例如，准确性)。我们称epoch为一个训练循环和一个验证循环的迭代。模型的输入应该是标准化的，可以将它们除以255: X /= 255。
运行python training.py来训练第一个机器学习模型!同时需要指定——imdir，例如——imdir GTSRB/Final_Training/Images/，使用提供的GTSRB数据集。
提示
在验证循环中不需要tf.GradientTape，因为不会更新梯度。assign_sub Variable方法对于在sgd优化器中执行权重更新非常有用。使用tf.one_hot函数从ground_truth标定中获取一个向量。

参考代码如下：

import argparse
import logging

import tensorflow as tf

from dataset import get_datasets
from logistic import softmax, cross_entropy, accuracy


def sgd(params, grads, lr, bs):
    """
    stochastic gradient descent implementation
    args:
    - params [list[tensor]]: model params
    - grads [list[tensor]]: param gradient
    - lr [float]: learning rate
    - bs [int]: batch_size
    """
    for param, grad in zip(params, grads):
        param.assign_sub(lr * grad / bs)


def training_loop(lr):
    """
    training loop
    args:
    - lr [float]: learning rate
    returns:
    - mean_acc [tensor]: training accuracy
    - mean_loss [tensor]: training loss
    """
    accuracies = []
    losses = []
    for X, Y in train_dataset:
        with tf.GradientTape() as tape:
            # forward pass
            X = X / 255.0
            y_hat = model(X)
            # calculate loss
            one_hot = tf.one_hot(Y, 43)
            loss = cross_entropy(y_hat, one_hot)
            losses.append(tf.math.reduce_mean(loss))

            grads = tape.gradient(loss, [W, b])
            sgd([W, b], grads, lr, X.shape[0]) 

            acc = accuracy(y_hat, Y)
            accuracies.append(acc)
    mean_acc = tf.math.reduce_mean(tf.concat(accuracies, axis=0))
    mean_loss = tf.math.reduce_mean(losses)
    return mean_loss, mean_acc

def model(X):
    """
    logistic regression model
    """
    flatten_X = tf.reshape(X, (-1, W.shape[0]))
    return softmax(tf.matmul(flatten_X, W) + b)


def validation_loop(val_dataset, model):
    """
    loop through the validation dataset
    """
    accuracies = []
    for X, Y in val_dataset:
        X = X / 255.0
        y_hat = model(X)
        acc = accuracy(y_hat, Y)
        accuracies.append(acc)
    mean_acc = tf.math.reduce_mean(tf.concat(accuracies, axis=0))
    return mean_acc


def get_module_logger(mod_name):
    logger = logging.getLogger(mod_name)
    handler = logging.StreamHandler()
    formatter = logging.Formatter('%(asctime)s %(levelname)-8s %(message)s')
    handler.setFormatter(formatter)
    logger.addHandler(handler)
    logger.setLevel(logging.DEBUG)
    return logger


if __name__  == '__main__':
    logger = get_module_logger(__name__)
    parser = argparse.ArgumentParser(description='Download and process tf files')
    parser.add_argument('--imdir', required=True, type=str,
                        help='data directory')
    parser.add_argument('--epochs', default=10, type=int,
                        help='Number of epochs')
    args = parser.parse_args()    

    logger.info(f'Training for {args.epochs} epochs using {args.imdir} data')
    # get the datasets
    train_dataset, val_dataset = get_datasets(args.imdir)

    # set the variables
    num_inputs = 1024*3
    num_outputs = 43
    W = tf.Variable(tf.random.normal(shape=(num_inputs, num_outputs),
                                    mean=0, stddev=0.01))
    b = tf.Variable(tf.zeros(num_outputs))

    lr = 0.1
    # training! 
    for epoch in range(args.epochs):
        logger.info(f'Epoch {epoch}')
        loss, acc = training_loop(lr)
        logger.info(f'Mean training loss: {loss:1f}, mean training accuracy {acc:1f}')
        val_acc = validation_loop()
        logger.info(f'Mean validation accuracy {val_acc:1f}')

10.其他优化器（Optimizers）
克服局部极小值问题的一种方法是增加动量项（momentum term）。 这种方法的灵感来自于物理学:当优化器在同一方向上连续执行多个步骤时，应该能够获得速度。 这个速度将帮助优化器克服局部最小值。

 

你可以在原文（https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.57.5612&rep=rep1&type=pdf）中读到更多关于动量的内容；

该文概述了深度学习中最常用的优化器:梯度下降优化算法的概述（https://arxiv.org/pdf/1609.04747.pdf） 
学习率和退火（Learning Rates and Annealing）
正如你将在后面项目中意识到的，学习速度在梯度下降方法的成功中扮演着关键的角色。 提高梯度下降算法性能的一种非常流行的方法是学习速率退火，即在训练过程中降低学习速率。 不同的退火策略，如逐步退火、余弦退火或指数退火；学习调度器也被使用。 

11.神经网络

 

前馈神经网络(FFNN)是logistic回归算法的扩展。 我们可以把逻辑回归看成是一个单层的FFNN。 FFNN是叠加多个隐藏层(任何非输入或输出层的层)，然后是非线性激活，如sigmoid或softmax激活。

 
FFNN只是由全连接的层组成，其中一层中的每个神经元与前一层中的所有神经元连接。  
让我们考虑一个包含n个神经元的FFNN层中的一个神经元。 前一层有m个神经元。这个神经元使用前一层的输出执行一个线性操作wX+b，这意味着X是一个mx1向量。 我们可以使用矩阵乘法来一次完成所有的运算，而不是在n个神经元中逐个循环。 这一层的输出将通过计算WX+B得到，其中B是偏差的mx1向量，W是权值的nxm矩阵。  
为了进一步简化，我们可以将偏置向量B合并到矩阵W中，这样W现在的维数是nx(m+1)。 我们只需要创建一个新的维度为(m+1)x1的输入向量X，其中X[m+1]=1，就可以得到与上面相同的结果。 

激活函数

 

​​​​激活函数在神经网络中起着至关重要的作用，因为它增加了系统的非线性。 最常见的激活函数是ReLU激活函数，但其他的激活函数如sigmoid或双曲正切也很流行。

12.反向传播（Backpropagation）

 

链式法则允许你分解复合函数导数的计算。 因为我们可以把神经网络想象成一个巨大的复合函数，链式法则是反向传播算法的核心。 反向传播是用来计算相对于神经网络的每个权重的损失梯度的机制。

 

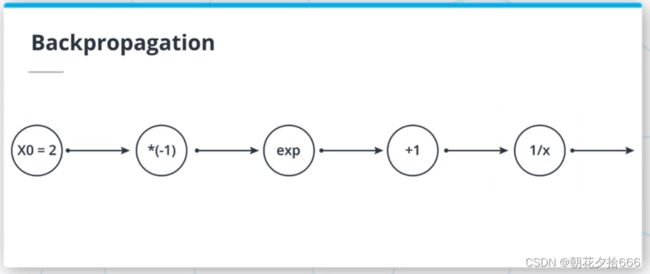
反向传播计算示例

回路方法是一种直观的方式来理解反向传播算法。 利用链式法则，我们可以将梯度从最后一个节点反向传播到第一个节点。  
例如，第三个节点的输入是-2，该节点对其输入应用指数函数。 该节点的输出为exp(-2) = 0.14。 当反向传播梯度时，我们在此节点前得到-0.77的值。 由于链式法则，由于指数函数的导数是指数函数，我们可以反向传播梯度:exp(-2) *(-0.77) = -0.10。

13.基于前馈神经网络的图像分类
因为前馈神经网络以向量作为输入，所以我们需要将HxWxC图像扁平化为(HxWxC)x1向量。神经网络训练训练神经网络是一个昂贵和漫长的过程。 因为在训练一个神经网络时，很多事情都可能出错，所以ML工程师照看训练过程是至关重要的。 可视化损失和度量将有助于识别训练过程中的任何问题，并允许工程师停止、修改、重启训练。14.练习3 - Keras
目的
在本练习中，学习如何利用Keras API创建小型神经网络。

细节
Keras最初是作为一个独立的API创建的，它提供了使用相同接口但不同后端库(如Tensorflow)创建和训练神经网络的简单方法。Tensorflow是一个低级（ low-level ）库，而Keras的代码库对初学者很友好。

本练习创建的神经网络应该少于4层，包括输出层。最后一层不应该被激活。花点时间对不同的架构(层数、神经元数)进行实验，看看它如何影响结果。需要指定——imdir，例如——imdir GTSRB/Final_Training/Images/，使用提供的GTSRB数据集。

提示
可以利用tf.keras.Sequential在您的网络中堆叠层，并利用tf.keras.layers创建不同的层。

参考代码如下： 

import argparse

import tensorflow as tf
from tensorflow import keras

from utils import get_datasets, get_module_logger, display_metrics


def create_network():
    """ output a keras model """
    model = tf.keras.Sequential([
        tf.keras.layers.Flatten(input_shape=(32, 32, 3)),
        tf.keras.layers.Dense(128, activation='relu'),
        tf.keras.layers.Dense(43)])
    return model


if __name__  == '__main__':
    logger = get_module_logger(__name__)
    parser = argparse.ArgumentParser(description='Download and process tf files')
    parser.add_argument('-d', '--imdir', required=True, type=str,
                        help='data directory')
    parser.add_argument('-e', '--epochs', default=10, type=int,
                        help='Number of epochs')
    args = parser.parse_args()    

    logger.info(f'Training for {args.epochs} epochs using {args.imdir} data')
    # get the datasets
    train_dataset, val_dataset = get_datasets(args.imdir)

    model = create_network()

    model.compile(optimizer='adam',
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
              metrics=['accuracy'])
    history = model.fit(x=train_dataset, 
                        epochs=args.epochs, 
                        validation_data=val_dataset)
    display_metrics(history)

其它资源

• Basic Image Classification：https://www.tensorflow.org/tutorials/keras/classification

15.本文总结
在本文中，主要有以下内容:
线性回归:对两个变量之间的线性关系进行建模的回归方法，介绍了L1和L2的损失。
逻辑回归:一种分类算法及一种分类损失，交叉熵损失。
梯度下降优化:一种寻找损失最小化问题最优解的迭代算法。
前馈神经网络:一种由完全连接的层组成的神经网络。
反向传播:一种利用链式法则计算神经网络中损失梯度的算法。
用神经网络进行图像分类:如何将图像在前馈神经网络中输入。

16.Glossary术语表
激活函数Activation function:神经网络中的非线性可微分函数。
反向传播Backpropagation:通过神经网络传播梯度的机制。
交叉熵Cross Entropy(CE)损失:一种损失函数，通过取真实值向量和输出概率向量的对数的点积来计算。
梯度下降Gradient descent:用于寻找损失函数最小值的迭代算法。
全局最小值Global minimum:损失函数取其整个定义域的最小值。
学习率Learning rate:标量控制梯度下降算法的步长。
局部最小值Local minimum:损失函数域的局部子集中的最小值。
平均绝对误差Mean Absolute Error/ L1损失:一个损失函数，通过对真实值和预测值的绝对差相加计算得出。
均方误差Mean Square Error (MSE) / L2损耗:一种损耗函数，其计算方法是将实际值和预测值的平方差相加。
优化器Optimizer:梯度下降算法的另一个名称。
张量Tensors:多维的TensorFlow数据结构，类似于numpy数组。
变量Variable:TensorFlow张量，可以通过操作进行更改。