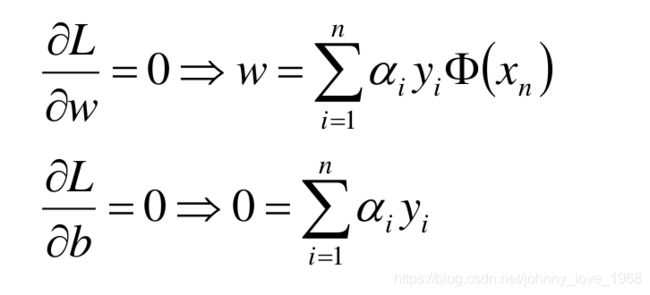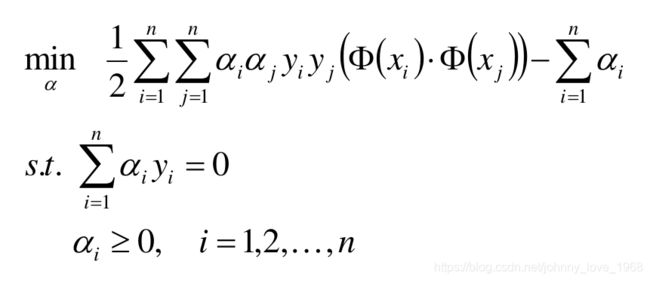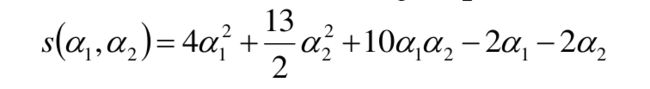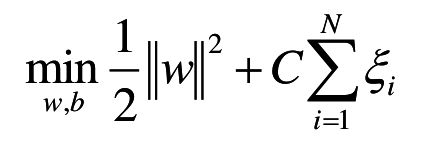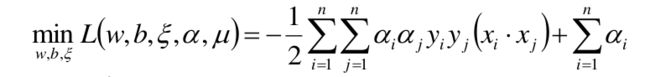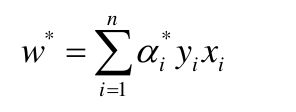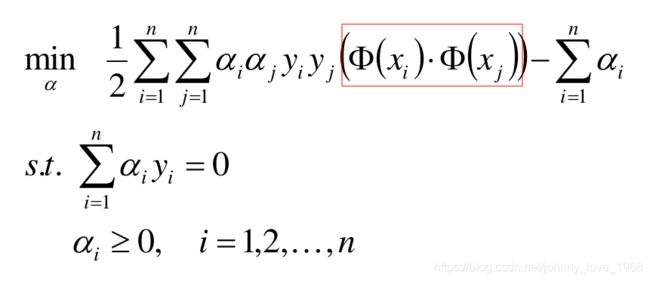SVM简介
SVM
文章目录
- SVM
-
- 一. 什么是SVM
-
- 1. 简介
- 2.SVM分类
- 二. 详细介绍
-
- 1. 线性可分SVM
-
- 1.1 支撑点,支撑向量
- 1.2 分割超平面与间隔最大化
- 1.3 线性可分SVM的目标函数以及相关算法
- 1.4 线性可分SVM的简单举例
- 2.线性SVM
-
- 2.1 为什么需要线性SVM
- 2.2 线性SVM相关理论
- 2.3 线性SVM算法
- 3.非线性SVM
-
- 3.1 核函数
- 3.2 核函数分类
-
- 3.2.1 多项式核函数
- 3.2.2 高斯核函数(RBF)
- 3.2.3 Sigmoid核函数
一. 什么是SVM
1. 简介
SVM,曾经是一个特别火爆的概念。它的中文名:支持向量机(Support Vector Machine, 简称SVM)。因为它红极一时,所以关于它的资料特别多,而且杂乱。虽然如此,只要把握住SVM的一些特点,至少可以做到思路清晰。
-
首先,SVM是按照监督类学习方式进行运作的。即:数据当中含有目标值。
-
SVM采用监督学习方式,对数据进行二分类(这点跟逻辑回归一样)。但是,SVM和逻辑回归(LR)有有很多不同点。我们先看看相同点:
- 二者都是线性分类器
- 二者都是监督学习算法
- 都属于判别模型(KNN, SVM, LR都属于判别模型),所谓判别模型就是指:通过决策函数,判别各个样本之间的差别来进行分类。
不同点就很多了,现在先列举一些,LR之前已经介绍过,关于SVM的具体理论先放到后面
-
二者的损失函数和目标函数不一样。
-
二者对数据和参数的敏感度不同。SVM由于采用了类似于“过度边界”的方式,泛化能力更好
……
-
SVM可以作线性分类器,但是在引入核函数(Kernel Method)之后,也可以进行非线性分类
2.SVM分类
SVM大体上可分为:
- 线性可分SVM:大体就是指一条线,把样本分成两份这种,我们会先从这个入手,这个相关理论懂了,后面的就会很简单
- 线性SVM
- 非线性SVM(需要核函数的支持)
二. 详细介绍
1. 线性可分SVM
1.1 支撑点,支撑向量
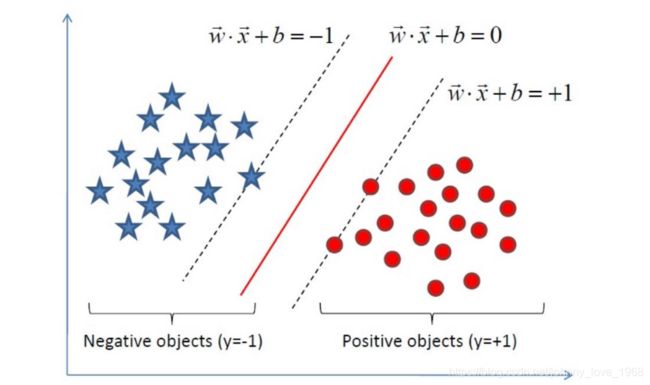
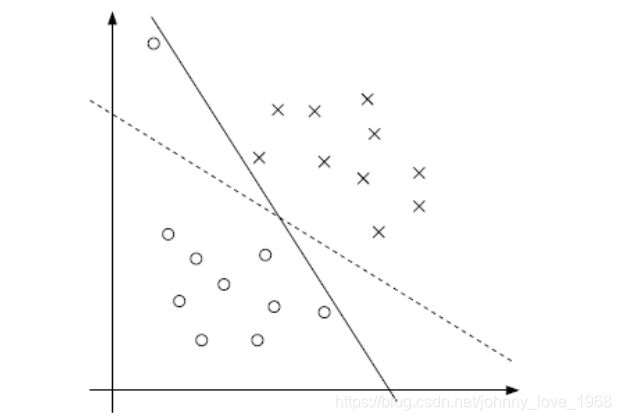
这个将作为重点来理解,这个相关理论知道了,那么,剩下的就很好理解,首先,我们先看一张图,然后我们根据这张图引出两个概念:支撑点,支撑向量。
我们看看图上面的三条线,首先,这是个二维平面,因此分割线可以表示成线性函数的形式:
f ( x ) = w T x + b f(x) = w^Tx + b f(x)=wTx+b
关于w,它其实是一个权值向量,它可以表示成如下的形式,至于说为什么能够这么表示,我们一会儿再说。
w → = ∑ i = 1 n α i x ( i ) y ( i ) \overrightarrow{w} = \sum_{i=1}^{n}\alpha_{i}x^{(i)}y^{(i)} w=i=1∑nαix(i)y(i)
在上图中,两个虚线之间,我们可以当做一个“过度区域”,在虚线上面,有一个蓝色的点,和两个红色的点正好位于虚线上面。对于这3个样本,我们标号1,2,3。我们大可以让alpha1,alpha2, alpha3不为0,其他的点alpha都是0。为什么可以这么做呢?因为边界的划定,也就是虚线,只受这三个边界点的影响(即:影响w向量)我们在现实中直接调整这三个边界点的alpha值,就可以确定界限。那么这三个点,我们就可以称他们为:**支撑点 **
如果你确定了一个起始点,那么起始点到各个点之间可以组成向量,这个起始点到支撑点之间就可以组成一个个:支撑向量
1.2 分割超平面与间隔最大化
首先,我们得知道什么是超平面?一般来说,二维就可以组成一个平面,那么如果是多维的呢?一般把超过二维的,就叫做超平面。由于超平面本身超出了一般人的认知,所以我们在理解分割超平面的时候,还是以最简单的二维平面入手,然后进行扩展。
在了解了什么是超平面之后,我们看这样一个图:
在这幅图中,我们看到了如此多的分割线,这些分割线都成功的把黑点和白点给区分开了。即:都把类别给分对了。那么,哪条线才是最优的呢?(如何分割超平面,就是解决这个问题)
我们就直接在二维空间一个基本问题入手:点到直线的距离入手。
我们假设有这么一条线:
l : f ( x , y ) = A x + B y + C l:f(x,y) = Ax + By + C l:f(x,y)=Ax+By+C
再给定一个点(x0, y0)那么这个点到直线的距离就是:
d ( x 0 , l ) = ∣ A x 0 + B y 0 + C ∣ A 2 + B 2 d(x_{0},l) = \frac{|Ax_{0} + By_{0} + C|}{\sqrt{A^2 + B^2}} d(x0,l)=A2+B2∣Ax0+By0+C∣
然后我们在此基础上直接把分子的绝对值给去掉,去掉之后,运算结果就会有正负之分了,通过正负,可以判断这个点在这条直线的哪一侧。然后各个项给拆开如下:
d ( x 0 , l ) = A A 2 + B 2 x 0 + B A 2 + B 2 y 0 + C A 2 + B 2 d(x_{0},l) = \frac{A}{\sqrt{A^2 + B^2}}x_{0} + \frac{B}{\sqrt{A^2 + B^2}}y_{0} + \frac{C}{\sqrt{A^2 + B^2}} d(x0,l)=A2+B2Ax0+A2+B2By0+A2+B2C
我们令各项系数分别记为:A’, B’ C’。然后整个公式就可以写成向量相乘的形式:
d ( x 0 , l ) = A ′ x 0 + B ′ y 0 + C ′ = ( A ′ , B ′ ) ( x 0 b 0 ) + C ′ = w → x + b d(x_{0},l) = A'x_{0} + B'y_{0} + C' = (A',B')(\begin{matrix}x_{0}\\b_{0}\end{matrix}) + C' = \overrightarrow{w}x + b d(x0,l)=A′x0+B′y0+C′=(A′,B′)(x0b0)+C′=wx+b
我们直接把(A’,B’)记为wi向量,将后面的(x0,y0)记为x向量 C’可以记为b,于是就得到了上述式子。
在这个例子当中,只是给了一个二维平面,实际情况下,有可能是多维的。此时w向量也是多维的,可以记为w = (w1,w2,w3……wn),其中这里的w1, w2对应的就是上面式子当中的A, B。我们再回过头看点到直线距离公式,看看那个分母。大致就可以猜出来一件事情:在多维空间中一个点到一个线的距离是:
d ( x 0 , l ) = w → x ( 0 ) + b ∣ ∣ w ∣ ∣ 2 d(x_{0},l) = \frac{\overrightarrow{w}x^{(0)} + b}{||w||_{2}} d(x0,l)=∣∣w∣∣2wx(0)+b
此时,我们再看看图一。注意,图一两条虚线线等号后面分别是+1,-1,为啥是这个呢?
假设我划分了一个线,那么显然,每一个点到这个线都会有一个距离,按照上面这个式子,求出来的距离是带有符号的,这个时候就体现出这个1,-1的价值。这个1,-1,也是y(i)值。如果,求出的是正的,那么乘以1,就是距离本身,如果d为负值,那么乘以-1,又转回正的,还是距离。这就是为什么真正的距离会写成。
d ( x i , l ) = ( w → x ( i ) + b ) y ( i ) ∣ ∣ w ∣ ∣ 2 ( 公 式 一 ) d(x_{i},l) = \frac{(\overrightarrow{w}x^{(i)} + b)y^{(i)}}{||w||_{2}}(公式一) d(xi,l)=∣∣w∣∣2(wx(i)+b)y(i)(公式一)
那么,我所有点,都跟这个直线求一个距离,最后取一个最小值。
我跟所有的直线,都做上面这个操作,就会得到若干个这样的最小值,然后我取最小值最大的那个直线,就是最优解。即:
m a x l = 1 , 2 , … … n [ m i n ( d ( x i , l ) ) ] ( 公 式 二 ) max_{l=1,2,……n}[min(d(x_{i},l))](公式二) maxl=1,2,……n[min(d(xi,l))](公式二)
对于这个方式,有一个很直观的名字:间隔最大化。
以上就是对分割超平面的一种直观的解释的一个解释。如果扩展到多维,即:超平面,很多时候,我们就不能用单纯一个x向量来解释了。其实,二维当中y与x是线性关系,也是一种映射关系。在多维平面当中,这种映射往往比较复杂,因此,扩展之后,我们会把间隔最大化的线写成如下形式:
y ( x ) = w T ϕ ( x ) + b y(x) = w^T\phi(x) + b y(x)=wTϕ(x)+b
其中,φ(x)是某个确定的特征空间转换函数,它的作用是将x映射到(更高的)维度。而在最简单的二维平面中φ(x)=x
由于在线性可分SVM是用来做分类问题,最基本的就是用来做二分类问题,所以,还要把上面这个式子映射到一个只有两个取值的函数当中,这就是线性可分SVM的决策函数:
f ( x ) = s i g n ( w T ϕ ( x ) + b ) f(x) = sign(w^T\phi(x) + b) f(x)=sign(wTϕ(x)+b)
1.3 线性可分SVM的目标函数以及相关算法
我们在图一当中,知道,虚线部分的y值取1,或者-1。但实际上,支撑点可不一定满足这个条件,类似的例子,可以举出无数个。因此,对于目标函数的构建,我们首先就要考虑一个问题:缩放。
根据题设,我们有一个间隔最大化的函数:
y ( x ) = w T ϕ ( x ) + b y(x) = w^T\phi(x) + b y(x)=wTϕ(x)+b
我们要让y(x)满足这个条件:
我们对w和b进行等比缩放,就得到了(回过头看看公式(一)):
于是,把这个与公式二结合起来看,我们就得到了目标函数:
缩放的理论知道了,我们下一步,就是想,怎么能让那个y值是1。对于分类来说,就是让各个类别的点,尽量远离过渡区域,也就是说,这些点离分割线的距离要大于或者等于1,这样才达到分类目的,如下图所示:那个margin大于1,分类才越准确。
用符号表示就是:
通过等比例缩放w的方法,使得两类点的函数值都满足| y |≥1
然后,我们把间隔函数代入:
y i ( w T ϕ ( x i ) + b ) > = 1 y_{i}(w^T\phi(x_{i}) + b) >= 1 yi(wTϕ(xi)+b)>=1
由于这部分大于或者等于1了,那么反过来看一看那个目标函数。由于大括号里面的min部分最小值就是1,那么我们就得到了一个新的目标函数:

于是,整个式子就转化为一个问题:
对 于 函 数 m a x w , b 1 ∣ ∣ w ∣ ∣ , 使 得 : y i ( w T ϕ ( x i ) + b ) > = 1 对于函数max_{w,b}\frac{1}{||w||}, 使得:y_{i}(w^T\phi(x_{i}) + b) >= 1 对于函数maxw,b∣∣w∣∣1,使得:yi(wTϕ(xi)+b)>=1
乍一看这个问题,是不是就是我们大学时候学到的一个重要知识点:条件极值。怎么求解条件极值呢?拉格朗日乘数法!
由于||w||本身是带有根号的,不方便计算。为了方便计算,我们换成:
1 2 ∣ ∣ w ∣ ∣ 2 \frac{1}{2}||w||^2 21∣∣w∣∣2
拉个朗日乘数法怎么一个流程的?首先引入必要的变量,构造一个新的函数。然后分别对自变量和引入的变量求偏导,令他们等于0,求出驻点。然后这几个驻点分别代入到原方程,看哪个是最大的,哪个是最小的。
首先,引入必要的变量,构造一个新的函数:
求驻点:
对上面这个式子进行求解,那么问题就会转化成如下这个式子:(alpha到底取什么值呢)
进一步转换(这个,也是线性可分SVM目标函数的最终形式),构成了一个新的条件极值问题
那么,我们就可继续用拉格朗日乘数法进行求解,然后,就求出了alpha*
1.4 线性可分SVM的简单举例
有了上面这些论述,到底怎么用呢?我们举一个例子:
我们给定3个数据点:正例点x 1 =(3,3) T ,x 2 ==(4,3) T ,负例点x 3 =(1,1) T ,求线性可分SVM,如下所示:
在求解这个问题的时候,我们不要忘了y的取值是1,或者-1。这个例子当中正例点x1,x2,他们对应的y一定是1所以说a1 = (3, 3, 1)。a2 = (4, 3, 1)。x3是负例点,所以a3 = (1, 1, -1)。然后把这些值分别带入目标函数。注意:减号前面是xi点乘xj。
然后我们这些值代入到目标函数,即公式三当中
我们将上面两个式子进行联立:将a1 + a2 = a3代入到min函数当中,得到:
然后,上面这个式子分别对a1, a2求偏导,令偏导为0进而求出驻点,然后把驻点代入到上面这个式子。最后得到:在a1 = 1.5, a2=0时取极值,但是呢,这个不满足a2>=0的条件,于是,我们在边缘地方进行验证(这一切都是考研数学当中的基本内容)
a1=0代入,知道当a2=2/13的时候,整个式子取极小值:-0.153
a2=0代入,知道当a1=1/4时,整个式子取极小值:-0.25
所以,a1 = 1/4, a2=0, 此时a3 = 1/4。
知道各个参数值了,我们可以分离超平面了。不用说,a1=a3=1/4, 对应的点一定是支撑点。我们把a1=1/4, a2=0, a3=1/4代入到公式二当中:

得到w1 = w2 = 0.5, b=-2
于是,分离超平面是:
1 2 x 1 + 1 2 − 2 = 0 \frac{1}{2}x_{1} + \frac{1}{2} -2 = 0 21x1+21−2=0
于是,分离决策函数:
f ( x ) = s i g n ( 1 2 x 1 + 1 2 − 2 ) f(x) = sign(\frac{1}{2}x_{1} + \frac{1}{2} -2) f(x)=sign(21x1+21−2)
2.线性SVM
2.1 为什么需要线性SVM
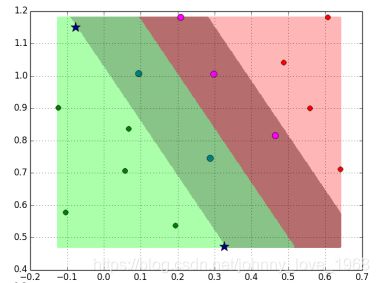
在实际运用当中,首先,即使数据是线性可分的。通过线性可分SVM得到的分离超平面也不一定就是最适合的。比如说下面这个图:
如果按照分割超平面理论,实线应该属于最优的。但是,虚线部分,过渡带比较宽,所以他的泛化能力更好,可以更大可能的避免过拟合。
其次,如果数据根本就不是线性可分(即:线性不可分)的呢?你根本无法通过一条线或面就分的很明白呢?这就是为什么,我们要考虑:线性支持SVM
所谓线性不可分,就是指:一个数据集不可以通过一个线性分类器(直线、平面)来实现分类。这样子的数据集在实际应用中是很常见的,例如:人脸图像、文本文档等。
2.2 线性SVM相关理论
为了2.1当中所提及的问题,尤其是线性不可分的问题,我们在原本的方程当中引入了一个松弛因子:
ξ i ≥ 0 \xi_{i}\geq0 ξi≥0
如此一来,约束条件就变成了:
y i ( w ⋅ x i + b ) ≥ 1 − ξ i y_{i}(w\cdot x_{i} + b)\geq 1-\xi_{i} yi(w⋅xi+b)≥1−ξi
怎么理解这个松弛因子呢?我们看一看下面这张图:
首先,中间的阴影部分,我们说了这么多,已经大概有数了,我们称之为“过渡区域”。过渡区域之外的点,由于他们已经在自己应该呆的地方了,因此他们被分类分的很准确,因此,他们的松弛因子为0。唯独需要调整的,就是阴影内部的这些点,他们距离阴影边缘有一段距离,如果能通过松弛因子将他们排除到阴影之外(或者说通过松弛因子,适当调整分界线阴影两侧分界线的位置),那么分类就会分的更优。
因此,关于这个松弛因子,我们完全可以理解为,它是每个点到阴影边缘线的距离。如果把这些距离都给弥补上了,分类就会分的更准确。从这个意义上说,各个松弛因子的累加可以被当作损失函数。
于是,在引入松弛因子之后,目标函数就变成了:
乍一看,就是L2正则化+损失函数的形式。其中,当中的C是一个超参数,可以理解成为学习率之类的东西。如果这个C非常大,那么整个式子就退化成了标准SVM(即:线性可分SVM)
我们知道,分割超平面和阴影两侧的直线的距离是1,如果阴影当中的点,离分割超平面的距离是0.2,那么它的松弛因子就是0.8,离分割超平面的距离是0.4,那么这个松弛因子就是0.6……因此,这个函数的图像是一个很简单的线性关系图像:
由于这个图像形状很像铰链。于是很多资料把这个损失函数称作Hinge损失。
2.3 线性SVM算法
通过2.2的介绍,我们可以看的出来线性SVM其实也是一个条件极值问题,同样可以用拉格朗日乘数法解决。这个条件极值问题如下:注意,这当中有两个约束条件
我们直接套用拉格朗日乘数法的套路:
首先,构造拉格朗日函数:
然后把这三个式子代入到拉格朗日函数当中:
和线性可分SVM一样,求出这个式子之后,我们就得想:alpha取什么值,上面这个式子才能取极大值呢?于是我们进一步转换成下面这个条件极值问题:
整理一下:
对于上面这个问题,我们还可以用一下拉格朗日乘数法。进而求出这个alpha值。我们记为:a*
然后呢,我们看公式四。把求得的解代入到公式四当中,于是得到:
对于超平面函数,还有一个b,这个b在线性SVM当中的求解有很多中方法。不像线性可分SVM那么确定。一般来说,往往取各个支撑点的线性部分,然后取一个均值。与此同时,必须要满足整个条件极值当中的限定条件:
此时,我们就得到了分离超平面:
w ∗ x + b ∗ = 0 w^*x + b^* = 0 w∗x+b∗=0
于是,分类决策函数就是:
f ( x ) = s i g n ( w ∗ x + b ∗ ) f(x)=sign(w^*x+b^*) f(x)=sign(w∗x+b∗)
3.非线性SVM
3.1 核函数
曾经听人做过一个比喻。如果把SVM当做导弹,那么核函数就相当于导弹中的弹药,是真正可以爆炸并产生杀伤力的。这个比喻很好的说明了核函数对于SVM的作用,那么怎么理解这个核函数呢?
实际上,我们在介绍上面两种类型的SVM的时候,已经有所涉及了。拿我们之前说的线性可分SVM举例,我们看看它的目标函数的最终形式:
注意中间红框标注的地方。如果我们对这当中的部分进行一个全新的定义:
κ ( x i , x j ) ≜ < ϕ ( x i ) , ϕ ( x j ) > = ϕ ( x i ) ⋅ ϕ ( x j ) \kappa(x_{i}, x_{j}) \triangleq<\phi(x_{i}),\phi(x_{j})> = \phi(x_{i})\cdot\phi(x_{j}) κ(xi,xj)≜<ϕ(xi),ϕ(xj)>=ϕ(xi)⋅ϕ(xj)
那么红框的部分其实就是核函数。如果我们是在最简单的二维平面当中,那么,phi(x) = x,这就是一种最简单的多项式核函数。
在对核函数有了一个直观的印象之后,我们就可以引出核函数的定义:
核函数是可以将原始输入空间映射到新的特征空间,从而,使得原本线性不可分的样本可能在核空间可分。
3.2 核函数分类
核函数大体可以分为三种:
- 多项式核函数
- 高斯核函数(RBF)
- Sigmoid核函数
在实际应用中,往往依赖先验领域知识/交叉验证等方案才能选择有效的核函数。如果,没有头绪,那么优先选择高斯核函数。为什么?一会儿在讲高斯核函数的时候说。
3.2.1 多项式核函数
κ ( x 1 , x 2 ) = ( x 1 ⋅ x 2 + c ) d \kappa(x_{1},x_{2}) = (x_{1}\cdot x_{2} + c)^d κ(x1,x2)=(x1⋅x2+c)d
其中d代表维度
我们先以最简单的c=0,d=2为例子说明一下:
κ ( x → , y → ) = ( x → ⋅ y → ) 2 ⇒ ( ∑ i = 1 n x i y i ) 2 = ∑ i = 1 n ∑ j = 1 n x i x j y i y j = ∑ i = 1 n ∑ j = 1 n ( x i x j ) ( y i y j ) = ϕ ( x → ) \kappa(\overrightarrow x , \overrightarrow y) = (\overrightarrow x \cdot\overrightarrow y)^2 \Rightarrow(\sum_{i=1}^{n}x_{i}y_{i})^2 = \sum_{i=1}^{n}\sum_{j=1}^{n}x_{i}x_{j}y_{i}y_{j} = \sum_{i=1}^{n}\sum_{j=1}^{n}(x_{i}x_{j})(y_{i}y_{j}) = \phi(\overrightarrow x) κ(x,y)=(x⋅y)2⇒(i=1∑nxiyi)2=i=1∑nj=1∑nxixjyiyj=i=1∑nj=1∑n(xixj)(yiyj)=ϕ(x)
如果我们取n=3 那么上面那个式子就是:
如果我们引入常量c呢?我们仍然以n=3, d=2为例:
我们会发现,其实这个直接被拆分了,于是变成了若干的项的加和,此时,我们扔取n=3,那么结果就是:
ϕ ( x → ) = ( x 1 x 1 x 1 x 2 x 1 x 3 x 2 x 1 x 2 x 2 x 2 x 3 x 3 x 1 x 3 x 2 x 3 x 3 2 c x 1 2 c x 2 2 c x 3 c ) \phi(\overrightarrow x) =\begin{pmatrix} x_{1}x_{1}\\ x_{1}x_{2}\\ x_{1}x_{3}\\ x_{2}x_{1}\\ x_{2}x_{2}\\ x_{2}x_{3}\\ x_{3}x_{1}\\ x_{3}x_{2}\\ x_{3}x_{3}\\ \sqrt{2c}x_{1}\\ \sqrt{2c}x_{2}\\ \sqrt{2c}x_{3}\\ c \end{pmatrix} ϕ(x)=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛x1x1x1x2x1x3x2x1x2x2x2x3x3x1x3x2x3x32cx12cx22cx3c⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞
不光是平方,如果是多次方呢?那么根据上面的例子,我们其实很容易就能推论:虽然数据膨胀了,但是通过拆项,我们就会发现对于计算而言,其实并没有增加多少复杂度。这体现出了多项式核函数的一个优点。
3.2.2 高斯核函数(RBF)
κ ( x 1 , x 2 ) = e ( − γ ∣ ∣ x 1 − x 2 ∣ ∣ 2 ) \kappa(x_{1},x_{2}) = e^{(-\gamma||x_{1}-x_{2}||^2)} κ(x1,x2)=e(−γ∣∣x1−x2∣∣2)
我们看看高斯核函数的表达形式,就会发现高斯核函数的含义是:以xi为中心,向外做指数级别的衰减。离这个中心越远,那么高斯核函数的值就会越发的趋近于0。也就是说,跟xi越来越不相似
如果有很多的点呢?那么每一个点都会有一个以他自己为中心的,这样的核函数,如下图所示:

我们看到有的点在上方,有的点在下方,为什么呢?我们知道,对于二分类问题,有的点是正例,有的点是负例。SVM的式子总会乘以一个yi,那么也就是说,如果是正例,这个凸起部分就位于上方,否则,就位于下方。
高斯核函数有一点非常重要:分类到什么程度,可以通过超平面来调整。我们看下面这幅图:
这幅图,不光说明了高斯核函数。其实所有核函数都是在干这样一个事情。最开始的数据是左侧这样的散点,我们通过升维,转变成为右侧的那个样子,然后在通过超平面(就是图中的Decision surface, 也许翻译成决策平面更好)。从中分割一下,就把数据分成了两个类别。
所以,我们回到核函数的定义,核函数又是怎么做到的把原始数据映射到新的特征空间中?为什么说“可能在核空间可分”?这个问题就解释清楚了。
高斯核函数具有很强的适用性,如果实践中没有头绪该用哪个了,优先考虑高斯核函数。为什么?因为高斯核函数其实是无穷维的,因为当中的指数函数部分,可以用泰勒展开,进而扩展到无穷维度。如下所示:
于是高斯核函数通过泰勒公式展开,就是:
这就解释了高斯公式理论上是无穷维度的原因。
3.2.3 Sigmoid核函数
这个,前面说了这么多,这个了解一下它具体是什么即可:
κ ( x 1 , x 2 ) = t a n h ( x 1 ⋅ x 2 + c ) , 其 中 t a n h ( x ) = e x − e − x e x + e − x \kappa(x_{1},x_{2}) = tanh(x_{1}\cdot x_{2} + c), 其中tanh(x) = \frac{e^x-e^{-x}}{e^x + e^{-x}} κ(x1,x2)=tanh(x1⋅x2+c),其中tanh(x)=ex+e−xex−e−x