【斯坦福CS224N学习笔记】01-Introduction and Word Vectors
CS224N-01-Introduction and Word Vectors
CS224N Home 【Stanford NLP】
Video 【Bilibili】
第一课的内容主要包含两个方面,一个是介绍如何表达词的含义,从传统的词表示方法引入分布式语义表达,引出word vector,第二个方面是讲解了word2vec的原理,从word2vec的损失函数和计算推导方面剖析了word vector的原理。尤其是最后的损失函数推导计算,从公式方面解释了优化词向量的内涵。
1、Human language and word meaning
第一部分从传统的词表示引入到word vector,传统的表示方式是独热编码,由分布式语义产出词向量。
Definition: meaning (Webster dictionary)
Common solution: WordNet
Problems with resources like WordNet:
- Great as a resource but missing nuance, 细微差别
- missing new meaning of words, 单词含义
- Subjective, 主观的
- Requires human labor to create and adapt, 需要人工
- Can’t compute accurate word similarity, 无法计算相似度
Representing words as discrete symbols
traditional NLP,a localist representation
Means one 1, the rest 0s
独热编码(ont-hot)
motel=[0 0 0 0 1 0]
hotel=[0 1 0 0 0 0]
但是独热编码的结果是,这些词向量都是正交的,并且不能表达语义相似度。orthogonal(正交)、no natural notion of similarity
解决方案就是learn to encode similarity in the vectors themselves
Representing words by their context

Distributional semantics: A word’s meaning is given by the words that frequently appear close-by
Word vectors (word embeddings): dense vector
Word meaning as as neural word vector - visualization

2、Word2vec: Overview
Word2vec (Mikolov et al. 2013) is a framework for learning word vectors.
Idea:
- a large corpus of text,首先有一个语料库
- 每个词给一个初始化的vector
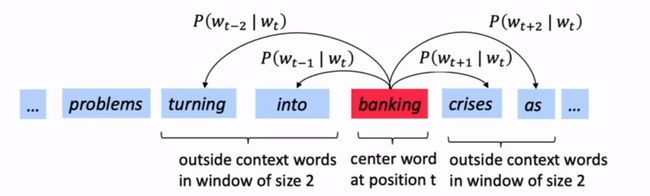
- 遍历text中的每个位置,包含了center word [c]和context words [o]
- 根据c和o的词向量的相似度来计算,给出c得出o的似然
- 调整优化word vectors来最小化似然
计算 P ( w t + j ∣ w t ) P(w_{t+j}|w_t) P(wt+j∣wt)
Word2vec: objective function
对于每一个text的位置 t = 1 , . . . , T t=1,...,T t=1,...,T,给出中心词 w j w_j wj,预测窗口为m内的上下文。
其似然值为:
L i k e l i h o o d = L ( θ ) = ∏ t = 1 T ∏ − m ≤ j ≤ m j ≠ 0 P ( w t + j ∣ w t ) Likelihood=L(\theta)=\prod_{t=1}^T\prod_{-m\le{j}\le{m} \atop{j\ne0}}P(w_{t+j}|w_t) Likelihood=L(θ)=t=1∏Tj=0−m≤j≤m∏P(wt+j∣wt) θ \theta θ is all variables to be optimized.
损失函数 J ( θ ) J(\theta) J(θ)是(平均)负的对数似然,negative log likelihood:
J ( θ ) = − 1 T l o g J ( θ ) = − 1 T ∑ t = 1 T ∑ − m ≤ j ≤ m j ≠ 0 P ( w t + j ∣ w t ) J(\theta)=-\frac{1}{T}logJ(\theta)=-\frac{1}{T}\sum_{t=1}^T\sum_{-m\le{j}\le{m} \atop{j\ne0}}P(w_{t+j}|w_t) J(θ)=−T1logJ(θ)=−T1t=1∑Tj=0−m≤j≤m∑P(wt+j∣wt)Minimizing objective function <==> Maxmizing predictive accuracy
想要最小化损失函数,首先要考虑怎么计算 P ( w t + j ∣ w t ) P(w_{t+j}|w_t) P(wt+j∣wt)
对于每个词给定两个词向量
- v w v_w vw,当w为中心词时
- u w u_w uw,当w为上下文时
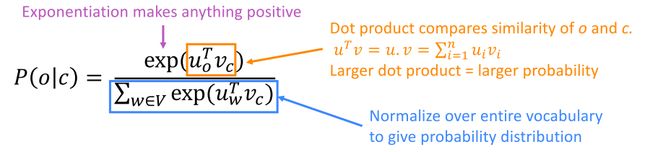
对于每个中心词c和上下文词o,有:
P ( o ∣ c ) = e x p ( u o T v c ) ∑ w ∈ V e x p ( u w T v c ) P(o|c)=\frac{exp(u_o^Tv_c)}{\sum_{w\in{V}}exp(u_w^Tv_c)} P(o∣c)=∑w∈Vexp(uwTvc)exp(uoTvc)分子上的向量点乘表达的是两个词的相似度,分母是中心词和所有词的相似度(注意:这里是所有词,后续优化)
softmax function:为什么成为softmax

To train the model: Compute all vector gradients
θ \theta θ represents all model parameters, in one long vector
Remember: every word has two vectors
计算偏导数,推导如下:(太妙了!)

上述推导中, P ( x ∣ c ) P(x|c) P(x∣c)是给定中心词 c c c,模型所给出的为 x x x 的概率。
这个推导结果很有趣!等号左边是给出中心词 c c c 其上下文 o o o 的对数概率的偏导,是我们要找的一个下降对快的一个方向,多维空间上的一个斜坡。等号右边的含义是,我们观察到的上下文的词 o o o ,从中减去我们的模型认为的上下文的样子,后面一部分是模型的期望。实际的上下文与模型认为的上下文,这两者之间的差异决定了下降的方向。