DeepLab V2 论文笔记

DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs

Deeplab v2

论文链接: https://arxiv.org/abs/1606.00915

一、 Problem Statement

图像语义分割有三个挑战:

1. 下降的分辨率
2. 目标的多尺度
3. localization的精度

对Deeplab V1 进行改进。

1. 把VGG-16改为ResNet。
2. 添加了ASPP。

二、 Direction

1. 空洞卷积, atrous convolution
2. ASPP, atrous spatial pyramid pooling
3. 全连接条件随机场，Fully-Connected Conditional Random Field(CRF)

三、 Method

1. 空洞卷积

重复堆叠max-pooling和striding会减少feature map的分辨率，位置信息难以恢复。作者使用atrous convolution来解决这个问题。空洞卷积可以在任何一层计算我们想要得到的分辨率大小。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gQ7bTSea-1628837840666)(image6.png)]

可以看到，上图的输入一个一维信号$x[i]$，输入一个一维信号$y[i]$，filter为$w[k]$，得出:
$$y[i]=\sum _{k=1}^{K}x[i+r\cdot k]w[k]$$
这里的$r$就是rate，对应于stirde，标准的卷积就是$r=1$。

假设是个二维输入信号，输入一张图片

atrous 卷积有两种实现方式:

1. 上采样卷积核，参数之间插入$r-1$个0。例如$K$大小的卷积核上采样之后大小为:$k+(k-1)(r-1)$
2. 下采样输入特征图，隔行去采样产生$r^2$个子特征图，然后正常卷积，最后插值返回输入大小的分辨率。

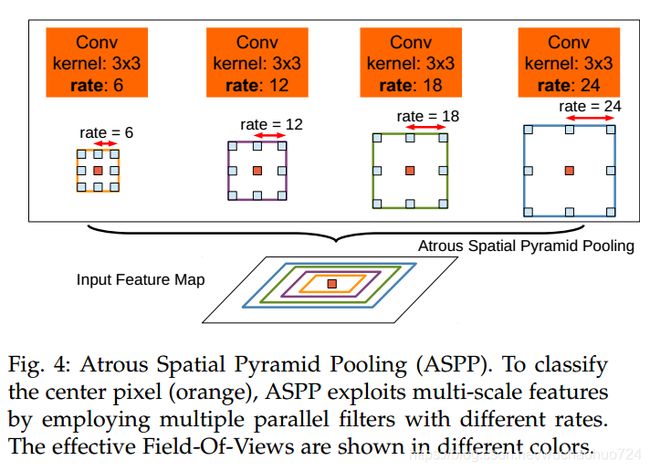
2. Atrous Spatial Pyramid Pooling(ASPP)

受到SPP的启发，作者使用了不同sampling rates的atrous convolution。具体结构如上。

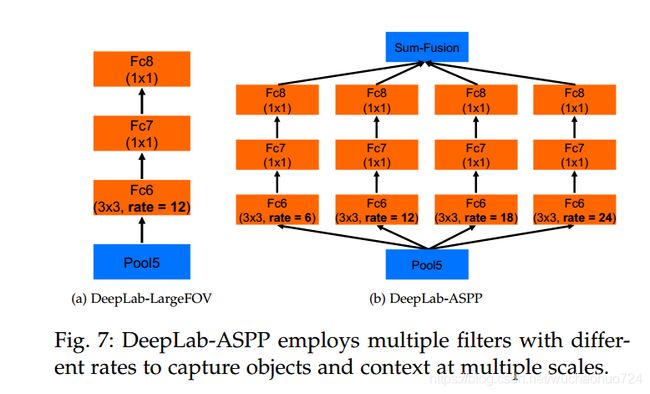
结合到网络中的具体操作如上图所示。

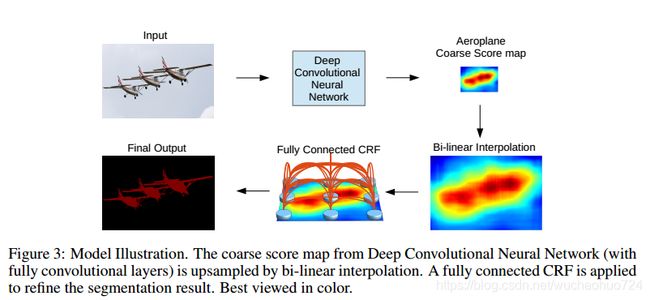
3. Boundary Recovery: Fully-Connected CRF

和deeplab v1是一样的。
传统的条件随机场是用来对segmentation maps进行噪声平滑处理的。比如short-range CRF, 它只考虑到目标像素点的附近点。我们的目标是恢复局部的细节而不是进一步平滑处理。因此，提出了Fully-Connected CRF。

它的energy function是:

$$E(x)=\sum _i{\theta }_i(x_i)+\sum _{ij}{\theta }_{ij}(x_i,x_j)$$
其中$x$是pixel的label。先看第一项，unary potential:
$${\theta }_i(x_i)=-logP(x_i)$$
也就是说，$P(x_i)$越大，这个值越小。保证了分类的准确率。

再看第二项, pairwise potential:
$${\theta }_{ij}(x_i,x_j)=\mu (x_i,x_j)\sum _{m=1}^K{w}_m\cdot k^m(f_i,f_j)$$
其中，
$$\mu (x_i,x_j)=\{\begin{array}{rl}& 1,\text{if}{x}_i\ne x_j\\ & 0,\text{otherwise}\end{array}$$

也就是说，只考虑标签不同的两个像素点，且因为是全连接，所以这两个点是模型中的任意两点。 $w_m$是权重，$k^m(f_i,f_j)$是高斯核函数:
$$w_1\exp (-\frac{||p_i-p_j|{|}^2}{2{\sigma }_{\alpha }^2}-\frac{||I_i-I_j|{|}^2}{2{\sigma }_{\beta }^2})+w_2\exp (-\frac{||p_i-p_j|{|}^2}{2{\sigma }_{\gamma }^2})$$

第一个核取决于pixel的positions和color intensities，第二个核只取决于position。

四、 Conclusion

我们提出的模型无法捕捉物体的微妙边界，例如自行车和椅子。由于unary term不够可靠，CRF后处理甚至无法恢复细节。我们假设encoder-decoder结构可以通过利用解码器路径中的高分辨率特征映射来缓解该问题。如何有效地结合该方法是一项未来的工作。

Reference

1. https://www.jianshu.com/p/2391704f0f81