（四）决策树与python代码实现ID3算法

李航老师《统计学习方法》第二版学习笔记

知识点：

• 决策树是一种基本的分类与回归方法，是基于树结构来进行决策的
• 根据损失函数最小化的原则建立决策树模型
• 决策树内部节点表示一个特征或属性，叶节点表示一个类
• 决策树可以看成if-then规则的集合
• 决策树的一条路径对应于划分中的一个单元
• 决策树常用的算法有ID3、C4.5与CART
• 决策树算法通常是一个递归的过程
• 决策树学习通常包含三个步骤：特征选择、决策树生成、决策树剪枝
• 信息熵表示随机变量不确定性的度量，熵越大不确定性就越大                  
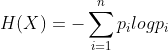
• 条件熵表示已知随机变量X的条件下随机变量Y的不确定性：
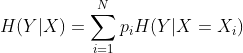
• 信息增益表示得知特征X的信息而使得类Y的信息不确定性减少的程度：
• 在特征选择中：ID3算法用信息增益准则选择特征，选择最大的
• 信息增益准则对可取值数量较多的属性有所偏好
• 在特征选择中：C4.5算法用信息增益比来选择特征
• 信息增益比准则对可取值数量较少的属性有所偏好
• 在特征选择中：CART算法用基尼指数来选择特征，选择最小的
• 基尼指数越小，数据集的混乱程度越小
• 剪枝是为了防止过拟合，即对已生成的树的简化，分为两种：预剪枝和后剪枝
• 预剪枝具有欠拟合风险，后剪枝时间开销大
• 决策树生成对应于模型的局部选择，决策树剪枝对应于模型的全局选择
• 对于连续值处理，采用二分法
• 对于缺失值处理
• 剪枝方法和程度对于决策树泛化性能的影响相当显著
• 多变量决策树是能实现斜划分或者更复杂划分的决策树

代码实现ID3算法

数据集：test1.txt

编号,色泽,根蒂,敲声,纹理,脐部,触感,好瓜
1,青绿,蜷缩,浊响,清晰,凹陷,硬滑,是
2,乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,是
3,乌黑,蜷缩,浊响,清晰,凹陷,硬滑,是
4,青绿,蜷缩,沉闷,清晰,凹陷,硬滑,是
5,浅白,蜷缩,浊响,清晰,凹陷,硬滑,是
6,青绿,稍蜷,浊响,清晰,稍凹,软粘,是
7,乌黑,稍蜷,浊响,稍糊,稍凹,软粘,是
8,乌黑,稍蜷,浊响,清晰,稍凹,硬滑,是
9,乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,否
10,青绿,硬挺,清脆,清晰,平坦,软粘,否
11,浅白,硬挺,清脆,模糊,平坦,硬滑,否
12,浅白,蜷缩,浊响,模糊,平坦,软粘,否
13,青绿,稍蜷,浊响,稍糊,凹陷,硬滑,否
14,浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,否
15,乌黑,稍蜷,浊响,清晰,稍凹,软粘,否
16,浅白,蜷缩,浊响,模糊,平坦,硬滑,否
17,青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,否

'''读取西瓜数据集'''
import numpy as np
import pandas as pd
df =pd.read_table('test1.txt',encoding='utf8',delimiter=',',index_col=0)


'''计算信息熵'''
import math
def info_entropy(df):
    class_num = len(df)
    class_1 = df[df["好瓜"]=="是"]
    class_0 = df[df['好瓜']=="否"]
    
    p_1 = len(class_1)/class_num
    p_0 = len(class_0)/class_num
    if p_1==0 and p_0!=0:
        info_entropy = -p_0*math.log2(p_0)
    elif p_0==0 and p_1!=0:
        info_entropy = -p_1*math.log2(p_1)
    else:
        info_entropy = -(p_1*math.log2(p_1)+p_0*math.log2(p_0))
    return info_entropy



'''划分数据集'''
def split_data(data_property,df):
    data_property_values = list(set(df[data_property]))
    data = [0]*len(data_property_values)
    for j,i in enumerate(data_property_values):
        data[j] = df[df[data_property]==i]
    return data



'''计算信息增益'''
def gain_func(data_property,df):
    df_len = len(df)
    dataset = split_data(data_property,df)
    dataset_num = len(dataset)
    entropy_Das = []
    dataset_each_nums =[]
    gain = {}
    for dataset_each in dataset:
        dataset_each_num = len(dataset_each)
        dataset_each_nums.append(dataset_each_num)
        # 计算分支节点的信息熵
        entropy_Da = info_entropy(dataset_each)
        entropy_Das.append(entropy_Da)
    # 计算信息增益
    entropy_D = info_entropy(df)
    entropy_condition = [entropy_Das[i]/df_len*y for i,y in enumerate(dataset_each_nums)]
    gain[data_property] = entropy_D-np.sum(entropy_condition)
    return gain



'''数据集中具有的属性'''
def propertys(root_property,df):
    data_propertys = []
    for column in df.columns:
        data_propertys.append(column)
    data_propertys.pop(-1)
    if root_property != None:
        data_propertys.remove(root_property)
    return data_propertys



'''确定划分属性'''
def choose_node(root_property,df):
    class_num = len(df)
    class_1 = df[df["好瓜"]=="是"]
    class_0 = df[df['好瓜']=="否"]
    if len(class_1)== class_num:
        print("叶节点：好瓜")
        # 这里如果为叶节点，返回其父节点
        return root_property
    elif len(class_0)== class_num:
        print("叶节点：坏瓜")
        # 这里如果为叶节点，返回其父节点
        return root_property
    else:
        gains = {}
        data_propertys = propertys(root_property,df)
        for data_property in data_propertys:
            gains.update(gain_func(data_property,df))
        gain_max_property = max(gains,key=gains.get)
        print("属性节点",gain_max_property)
        return gain_max_property



'''生成树，按层生成'''
current_node = choose_node(None,df)
nodes = []
nodes_data = []
def tree(father_node,df):
    if nodes!=[]:
        nodes.pop(0)
        nodes_data.pop(0)
    data = split_data(father_node,df)
    for branch_data in data:

        print("结点{'",father_node,"'}=",set(branch_data[father_node]),"的分支节点为")
        child_node = choose_node(father_node,branch_data)
        print("\n")
        if child_node==father_node:
            continue
        else:
            nodes.append(child_node)
            nodes_data.append(branch_data)
    for i,node_i in enumerate(nodes):
        # 递归
        tree(node_i,nodes_data[i])
        
        
        
tree(current_node,df)

 输出结果：与西瓜书上结果一致

属性节点 纹理
结点{' 纹理 '}= {'稍糊'} 的分支节点为
属性节点 触感
结点{' 纹理 '}= {'清晰'} 的分支节点为
属性节点 根蒂
结点{' 纹理 '}= {'模糊'} 的分支节点为
叶节点：坏瓜
结点{' 触感 '}= {'硬滑'} 的分支节点为
叶节点：坏瓜
结点{' 触感 '}= {'软粘'} 的分支节点为
叶节点：好瓜
结点{' 根蒂 '}= {'蜷缩'} 的分支节点为
叶节点：好瓜
结点{' 根蒂 '}= {'稍蜷'} 的分支节点为
属性节点 色泽
结点{' 根蒂 '}= {'硬挺'} 的分支节点为
叶节点：坏瓜
结点{' 色泽 '}= {'青绿'} 的分支节点为
叶节点：好瓜
结点{' 色泽 '}= {'乌黑'} 的分支节点为
属性节点 触感
结点{' 触感 '}= {'硬滑'} 的分支节点为
叶节点：好瓜
结点{' 触感 '}= {'软粘'} 的分支节点为
叶节点：坏瓜