特征变换:特征归一化(Normalization)作用以及方法 Min-Max、Z-Score
- 为什么需要对特征数据进行归一化?
1)、在基于梯度下降的算法中,使用特征归一化方法将特征统一量纲,能够提高模型收敛速度和最终的模型精度。1
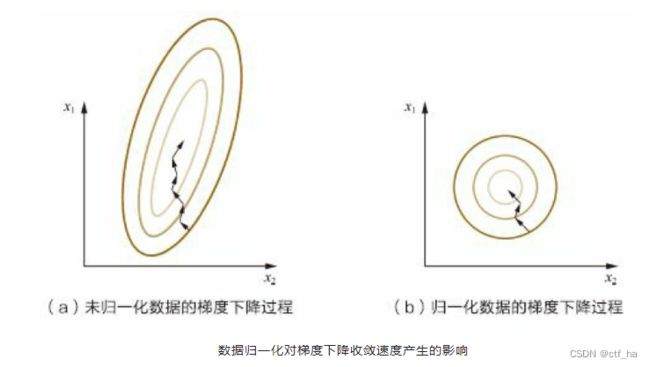
如上图所示,黄色的圈圈图代表的是两个特征的等高线。其中左图两个特征 X1 和 X2 的区间相差非常大,X1 区间是[0,2000],X2 区间是[1,5],其所形成的等高线非常尖。当使用梯度下降法寻求最优解时,很有可能走“之字型”路线(垂直等高线走),从而导致需要迭代很多次才能收敛;而右图对两个原始特征进行了归一化,其对应的等高线显得很圆,在梯度下降进行求解时能较快的收敛。因此如果机器学习模型使用梯度下降法求最优解时,归一化往往非常有必要,否则很难收敛甚至不能收敛。
2)、 归一化有可能提高精度。
一些分类器需要计算样本之间的距离(如欧氏距离),例如 KNN。如果一个特征值域范围非常大,那么距离计算就主要取决于这个特征,从而与实际情况相悖(比如这时实际情况是值域范围小的特征更重要)。
- 常用的两种方法:Min-Max、Z-Score、非线性归一化
1.线性函数归一化(Min-Max Scaling)
也称为极差法,是对原始数据的一种线性变换,使得原始数据映射到[0-1],实现对原始数据的等比缩放。
其公式如下:
X n o r m = X − X m i n X m a x − X m i n X_{norm}=\frac{X-X_{min}}{X_{max}-X_{min}} Xnorm=Xmax−XminX−Xmin
这种归一化方法比较适用在数值比较集中的情况。缺陷如果 max 和min 不稳定,很容易使得归一化结果不稳定,使得后续使用效果也不稳定。实际使用中可以用经验常量值来替代 max 和 min
2.零均值归一化(Z-Score Normalization)
也称为标准化分数,根据原始数据的均值和标准差将数据映射到均值为0,标准差为1的分布上。要求经过处理的数据符合标准正态分布。
其公式如下:
X n o r m = X − u σ X_{norm}=\frac{X-u}{σ} Xnorm=σX−u
相似点:
两种处理的本质都是对数据做线性变换,将数据压缩到[0,1]区间或者最大标准差之间的范围,消除特征量纲对模型训练的影响
不同点:
归一化的缩放仅跟最大和最小值相关;而标准化的缩放和每个点都有关系,通过均值和方差体现出来归一化的输出范围在0-1之间;而标准化的输出范围是与数据的标准差相关。
sklearn中标准化与归一化区别
从功能上划分,sklearn中的归一化其实是分为标准化(Standardization)和归一化(Normalization)两类。其中,此前所介绍的Z-Score标准化和0-1标准化,都属于Standardization的范畴,而在sklearn中,Normalization则特指针对单个样本(一行数据)利用其范数进行放缩的过程。不过二者都属于数据预处理范畴,都在sklearn中的Preprocessing 模块下。
- 标准化 Standardization
sklearn的标准化过程,即包括Z-Score标准化,也包括0-1标准化,并且即可以通过实用函数来进行标准化处理,同时也可以利用评估器来执行标准化过程。
实用函数进行标准化处理,尽管从代码实现角度来看清晰易懂,但却不适用于许多实际的机器学习建模场景。其一是因为在进行数据集的训练集和测试集切分后,我们首先要在训练集进行标准化、然后统计训练集上统计均值和方差再对测试集进行标准化处理,因此其实还需要一个统计训练集相关统计量的过程;其二则是因为相比实用函数,sklearn中的评估器其实会有一个非常便捷的串联的功能,sklearn中提供了Pipeline工具能够对多个评估器进行串联进而组成一个机器学习流,从而简化模型在重复调用时候所需代码量,因此通过评估器的方法进行数据标准化,其实是一种更加通用的选择。
# Z-Score标准化的评估器实现方法
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
StandardScaler?# 查阅参数
X = np.arange(15).reshape(5, 3) # 导入数据
scaler = StandardScaler()
X_train, X_test = train_test_split(X)
scaler.fit(X_train)
# 利用训练集的均值和方差对训练集进行标准化处理
scaler.transform(X_train)
# 利用训练集的均值和方差对测试集进行标准化处理
scaler.transform(X_test)
# 也可以使用fit_transform对输入数据进行直接转化
scaler = StandardScaler()
# 一步执行在X_train上fit和transfrom两个操作
scaler.fit_transform(X_train)
scaler.transform(X_test)
# 0-1标准化的评估器实现方法
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit_transform(X)
- 归一化 Normalization
和标准化不同,sklearn中的归一化特指将单个样本(一行数据)放缩为单位范数(1范数或者2范数为单位范数)的过程,该操作常见于核方法或者衡量样本之间相似性的过程中。同样,归一化也有函数实现和评估器实现两种方法。
假设向量 x = [ x 1 , x 2 , . . . , x n ] T x = [x_1, x_2, ..., x_n]^T x=[x1,x2,...,xn]T,则向量x的1-范数的基本计算公式为:
∣ ∣ x ∣ ∣ 1 = ∣ x 1 ∣ + ∣ x 2 ∣ + . . . + ∣ x n ∣ ||x||_1 = |x_1|+|x_2|+...+|x_n| ∣∣x∣∣1=∣x1∣+∣x2∣+...+∣xn∣
即各分量的绝对值之和。而向量x的2-范数计算公式为:
∣ ∣ x ∣ ∣ 2 = ( ∣ x 1 ∣ 2 + ∣ x 2 ∣ 2 + . . . + ∣ x n ∣ 2 ) ||x||_2=\sqrt{(|x_1|^2+|x_2|^2+...+|x_n|^2)} ∣∣x∣∣2=(∣x1∣2+∣x2∣2+...+∣xn∣2)
即各分量的平方和再开平方。
而sklearn中的Normalization过程,实际上就是将每一行数据视作一个向量,然后用每一行数据去除以该行数据的1-范数或者2-范数。具体除以哪个范数,以preprocessing.normalize函数中输入的norm参数为准。
from sklearn.preprocessing import Normalizer
# 1-范数单位化过程
normlize = Normalizer(norm='l1')
normlize.fit_transform(X)
# 2-范数单位化过程
normlize = Normalizer(norm='l2')
normlize.fit_transform(X)
非线性归一化
经常用在数据分化比较大的场景,有些数值很大,有些很小。通过一些数学函数,将原始值进行映射。该方法包括 log、指数,正切等。需要根据数据分布的情况,决定非线性函数的曲线,比如 log(V, 2)还是 log(V, 10)等。
为什么树型结构不需要做缩放?
因为数值缩放不影响分裂点位置,对树模型的结构不造成影响。按照特征值对数据进行排序,排序的顺序不变,那么分裂点就不会不同。
对于线性模型,特征值差别很大时,运用梯度下降的时候,损失等高线是椭圆形,需要进行多次迭代才能到达最优点。而对于归一化的数据,损失等高线是圆形,更少的迭代次数即可到达最优点。树模型不使用梯度下降,因为构建树模型相当于寻找最优分裂点,因此树模型是阶跃的,在阶跃点处不可导。
哪些机器学习算法不需要做归一化处理?
概率模型不需要归一化,因为它们不关心变量的值,而是关心变量的分布和变量之间的条件概率,如决策树、RF。而像 Adaboost、GBDT、XGBoost、SVM、LR、KNN、KMeans 之类的最优化问题就需要归一化。
取自[白面机器学习] ↩︎