【优秀论文解读】BoW3D: Bag of Words for Real-time Loop Closing in 3D LiDAR SLAM

论文简介

本论文新颖性在于3D激光雷达中实时闭环 且能够实时进行回环矫正 词袋模型为BoW3D 实时构建词袋 效率高 但是鲁棒性未知

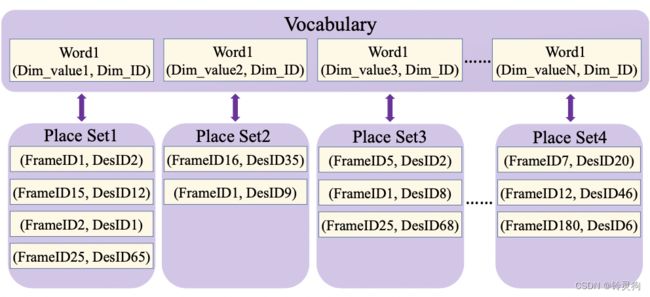
词袋存储

word包含两种变量：Dim_value为描述子计算得到的非零数和Dim_ID为word相对应的维度数 具体的计算可以查看论文：Link3d关键点的计算

Place Set为一张图片中的word集合 包含两种变量：FrameID为第几帧和DesID为一帧画面中的描述子的ID号、

Place Set记录了word出现在第几帧中的第几个描述子

优点：不需要加载额外的单词文件 且hash表的查找需要的时间复杂度很低 对于检索来说大大的提高了效率

类似于tf-idf的处理方式

当一个word出现次数过多并且超过了阈值时 认为这个特征比较普通 为了提高检测效率将不对这种word做记录

tf-idf的处理方式为：
$$tf-idf=\frac{n_{wi}}{n_i}\log \frac{N}{n_w}$$
$n_{wi}$为单词w在第i帧图片中出现的次数
$n_i$为图片中的单词总数
$N$所有的图片数 即当前记录了多少帧
$n_w$单词w在所有图片中出现的总次数
意思是如果单词w出现的次数越多 那么这个w的tf-idf得分就越高 表明这个word不适合用来分类

本文的做法使用一种类似于tf-idf的方法 目的同样是为了提高检索效率：
$$\text{ ratio }=N_{\text{set }}/\left(\frac{N}{n_w}\right)$$
$N_{set}$为word对应的place set中包含的place个数（参考上面的图片）
$N$为place的总数
$n_w$为总的单词数

如果这个数值高于了阈值 那么这个word对应的place set将不会再被计算

回环矫正

构建误差方程：
$$\begin{array}{c}{r}_{l,c}\left({\mathbf{R}}_{l,c},{\mathbf{t}}_{l,c}\right)=\frac{1}{2}{\sum }_{i=1}^n{\Vert s_l^i-\left({\mathbf{R}}_{l,c}{s}_c^i+{\mathbf{t}}_{l,c}\right)\Vert }^2\end{array}$$
$l$为回环检测到的历史帧的点云
$c$为当前帧的点云
$s$为激光点
求解R t的方法：
$$\mathbf{W}=\sum _{i=1}^n{\hat{\mathbf{s}}}_l^i{\hat{s}}_c^{iT}$$
$$W=U\Sigma V^T$$
$$R_{l,c}=V{U}^T$$
$$t_{l,c}=s^{,}-R_{l,c}s$$
$s_l{s}_c$为去中心化的点云坐标 剩下的应该都不用太解释

检测回环

1. Link3D的描述子作为输入且维护一个记录该帧每个place出现频率的hash table
2. 获得每一个Link3D描述子中的word对应的place set
3. 为每一个place set计算ratio 如果某个单词的频率过高 则直接进入下一次循环
4. 如果没有大于阈值 则遍历这个单词对应的place set中的每一个place
5. 如果这个place在hash表中 则该place的频率加一 如果没有出现过 则把这个place加到hash表中
6. 计算这个hash table中频率最高的place 如果高于了阈值 则认为这一帧是他的回环历史帧

原文的伪代码：

还有一个更新词典的策略 过于简单 不做文字详解：

优化全部相关变量

$i,j$两帧之间的残差定义为：
$$\begin{array}{c}{r}_{i,j}\left({\mathbf{T}}_{w,i},{\mathbf{T}}_{w,i}\right)=\ln {\left({\mathbf{T}}_{i,j}^{-1}{\mathbf{T}}_{w,i}^{-1}{\mathbf{T}}_{w,j}\right)}^{\vee }\end{array}$$
$$\begin{array}{c}{\min }_T\left\{{\sum }_{(i,j)\in S}{\Vert r_{i,j}\Vert }^2+{\sum }_{(i,j)\in L}{\Vert r_{i,j}\Vert }^2\right\}\end{array}$$
$S$为所有相邻的边的集合
$L$为回环检测的边
全部都会使用Levenberg-Marquadt方法在g2o上优化