数据挖掘知识点整理（期末复习版）

第一章 绪论

数据挖掘产生的背景？驱动力是什么？

DRIP（Data Rich，Information Poor）

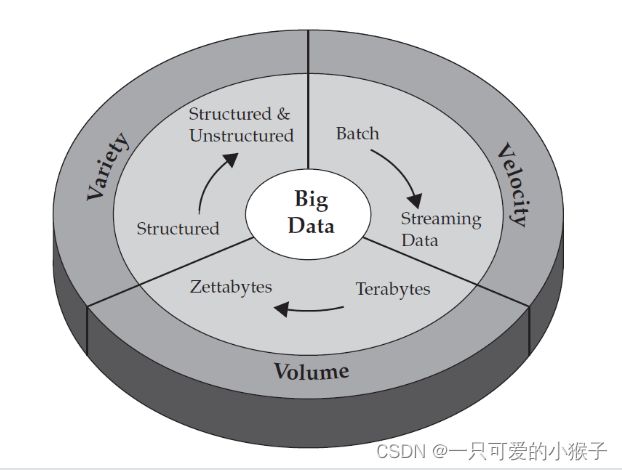
大数据的特点是什么？

3v : volume、velocity、Varity
数据量由TB级发展到ZB级
数据多样性从结构化转变为非结构化和结构化数据
数据传输的速度非常快
大数据导致难以应对的存储和计算量

什么是数据挖掘？

数据挖掘就是从数据中发现知识。
从大量的数据中挖掘哪些令人感兴趣的、有用的、隐含的、先前未知的、和可能有用的模式或知识。
数据挖掘并非全自动的过程，在各个环节都可能需要人为参与。

数据挖掘一般流程是什么？

业界数据整合&分析的过程是怎样的？

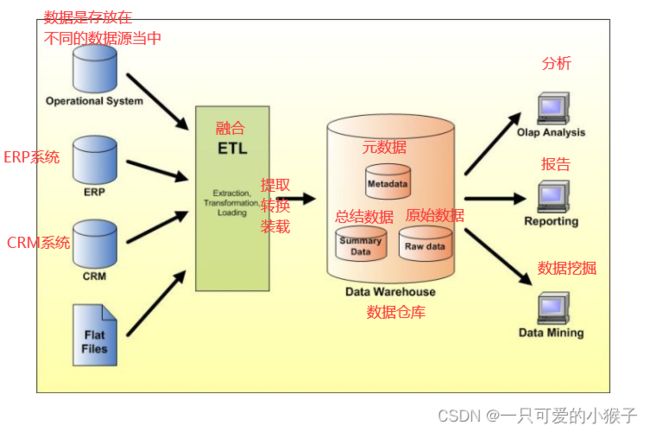
把数据从各个数据源当中提取出来，然后进行一些清洗融合（提取转换装载），这些数据处理完，才能把它合在一起，然后装在数据仓库当中，再取数据仓库中的数据去做各种各样的分析挖掘。

### 举例数据挖掘在各个领域的应用 **公共安全**：挖掘犯罪的规律，预防犯罪或者是减少犯罪的发生 **个性化医疗**：对DNA进行分析，根据基因的不同，更加的对症下药 **城市规划**：利用大数据来分析不同时段的交通热力图，来协助工作人员布局路线 **精准销售**：利用客户信息，实施精准推荐 **运动**：利用数据分析挑选身价低的潜力股运动员

数据挖掘的四大主要任务？他们的区别是什么？

主要任务：聚类分析、分类预测、关联分析、异常检测。

区别：
分类是利用标签进行模型构建，再利用模型进行预测，是有监督的学习方法
聚类是通过最小化簇内距离，最大化簇间距离，是无监督的学习方法

结合分类，介绍数据挖掘中常见的概念

什么是分类边界？

通过构建模型学习这样的分类边界，分类边界可以是分类线，分类面也可以是超平面。

什么是过拟合？

训练出来的分类边界过分的拟合训练数据，可能会导致模型在训练集中效果好，在测试集中效果不好

什么是混淆矩阵？

评价指标：
TPR = TP / (TP + FN)（真正正确的值中预测值为正确的比例）
TNR = TN / (TN + FP) （真正错误的值中预测值为错误的比例）
Accuracy = (TP + TN) / (P + N) （所有实际结果中预测正确的比例）

什么是ROC曲线/AUC评价标准？

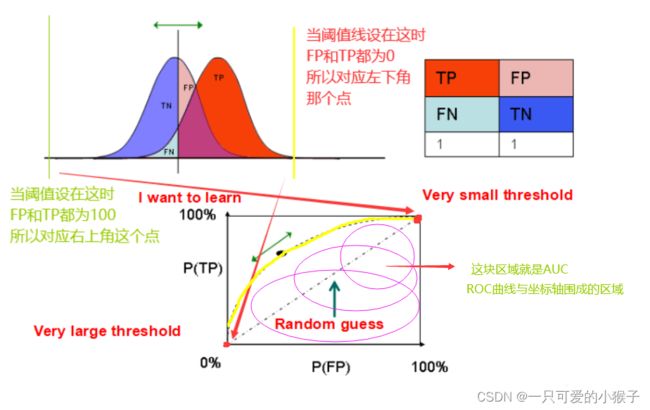
什么是代价敏感学习？

混淆矩阵中有两种错误，一种是正的预测成负的；一种是负的预测成正的
实际问题当中，这两种错误放在一起，错误成本的代价有所不同，所以在学习时要有所侧重的减轻错误代价成本高的错误情况
例如：就医过程中，真正生病的被诊断为无病，没有生病的被诊断为有病，肯定是前者错误代价更大，因此减少前者情况的发生

第二章 数据

数据属性类型

分为：连续性和离散型

什么叫做非对称属性？

只重视少部分非零属性值才有意义，称该属性为非对称属性（例如：超市购物，只在乎你买了哪些物品，而不会在乎你没买哪些东西）

数据集的一般特性

(1)维数
是数据集中属性的数目。分析高维数据时容易陷入维度灾难。数据预处理的一个重要动机就是减少维度，及维归约。
(2)稀疏性
有的数据集如非对称属性的数据集，非零项还不到1%, 这样可以仅存储非零值，将大大减少计算时间和存储空间。有算法专门针对稀疏数据（稀疏矩阵）进行处理。
(3)分辨率
不同采集频率可以获得不同分辨率的数据。例如：几米分辨率的数据，地球很不平坦，但若数十公里分辨率的数据，却相对平坦。数据模式依赖于分辨率。分辨率太小，模式可能不出现。分辨率太大，模式可能看不出。

什么是维度灾难？

为了得到更好的分类效果，我们可以加更多特征，但当我们特征多到一定时候时，分类器的效果反而开始下降了。

如何理解维度灾难？

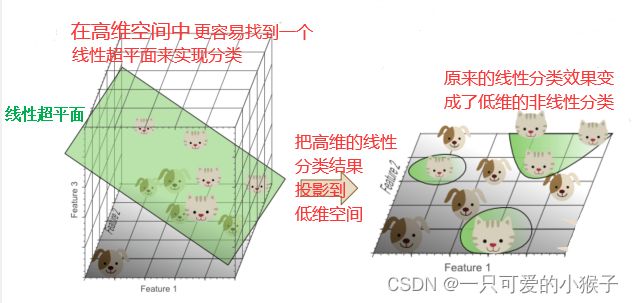
高维的分类器学习了训练数据的噪声和异常，而对样本外数据拟合效果不理想。导致了过拟合。
换句话说，随着维度的增加，但是数据是固定的，所以数据在特征空间中越来越稀疏，使得模型容易过拟合，学习了噪声和异常值，从而出现维度灾难。

如何避免维度灾难？

（1）训练数据的量
理论上说，训练样本的数量要求随指数增加（无限多），维度灾难就不会发生。
（2）模型的类型
非线性决策边界的分类器，如神经网络、KNN，决策树，分类效果好，但是泛化能力差。
因此，使用这些分类器时维度不能过高，而是需要增加数据量。
而如果是泛化能力好的分类器，如贝叶斯、线性分类器，可以使用更多的特征。

数据集有哪些类型？

(1)记录数据（数据矩阵、交易数据、文本数据）
数据集的常用标准形式是数据矩阵。（数据对象具有相同的数值属性集）（就是一个表格）

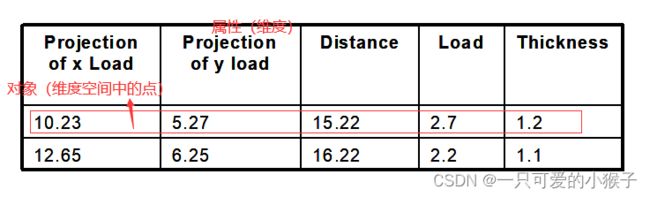
什么是词袋模型？（每个文档表达为词向量；每个词为向量的一个分量；每个分量的值为该词在文档中出现的次数。）

（2）图数据（万维网、分子结构）
（3）序列数据（时间序列、空间数据、图像数据、视频数据）

有哪些常见的数据质量问题？

数据质量差会对许多数据处理工作产生负面影响（例如：一些信誉良好的人被拒绝贷款）
常见数据质量问题: 噪声、异常值、缺失值、重复值、不一致值、不均衡数据
噪声(Noise)：是无关的数据对象
异常值(Outliers)：是数据对象，但其特征与数据集中大多数对象有显著不同

数据的相似性与相异性度量

相似性度量：度量数据对象的相似程度。越相似，值越高；值一般落在 [0,1]。
相异性度量：度量数据对象的相异程度。越不相似，值越高；值一般落在 [0,+)，上界不定。
相似性度量方法：二元向量相似度（SMC、Jaccard系数）、余弦相似度、皮尔森相关性
相异度量方法：Euclidean 距离、Minkowski 距离、马氏距离

二元向量间的相似性度量

多元向量间的相似性度量（余弦相似性）

皮尔森相关系数

相关系数（x, y) = 协方差（x, y) / (标准差（x） * 标准差（y））
相关性为【-1， 1】的线性相关，因此非线性函数的变量之间是不相关关系（相关系数为0）
皮尔森检验只能证明变量的线性相关性，两变量是否相关，可以使用卡方检验

Euclidean 距离

Minkowski 距离

闵可夫斯基距离(Minkowski distance) 是Euclidean距离的一个推广

其中 r 是参数, n 是维数（属性），xk 和 yk 分别是 x 和 y的第k个属性(分量) 。
r = 1. 曼哈顿距离（Manhattan，L1范数）
r = 2. 欧几里得距离（Euclidean，L2范数 ）
r-> ∞. 上确界距离(Lmax 或 L∞ 范数)

马氏距离

马氏距离优点：
（1）不受量纲的影响
马氏距离除以了一个协方差矩阵，这就把各个分量之间的方差都除掉了，消除了量纲性，两点之间的马氏距离与原始数据的测量单位无关，更加科学合理。
（2）马氏距离还可以排除变量之间的相关性的干扰

第三章 数据预处理

为什么需要数据预处理？

因为真实的数据是非常“dirty”，数据繁多，可能会出现以下的问题

数据预处理的主要任务？

数据清理

数据缺失

如何处理数据缺失

异常数据

测量变量中的随机错误(Noise)或偏差(Outlier)
也就是噪声和异常值

如何平滑异常值（主要针对异常值）？

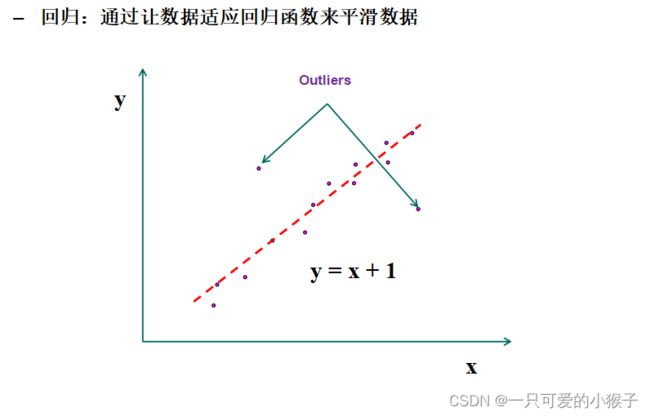
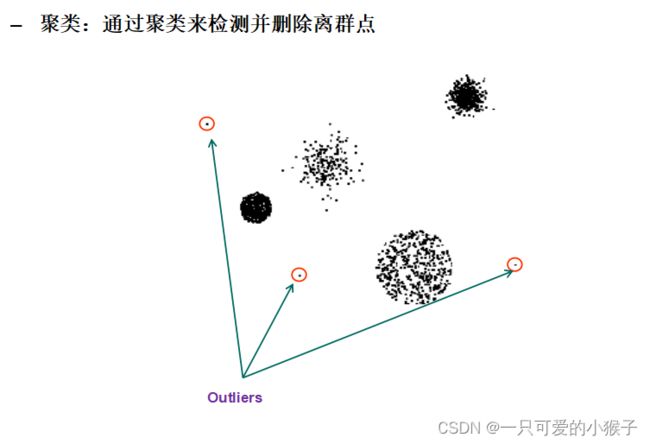
类型转换

属性的类别有以下几种，可以通过编码等方式实现任意转换

离散化（连续性变离散型）

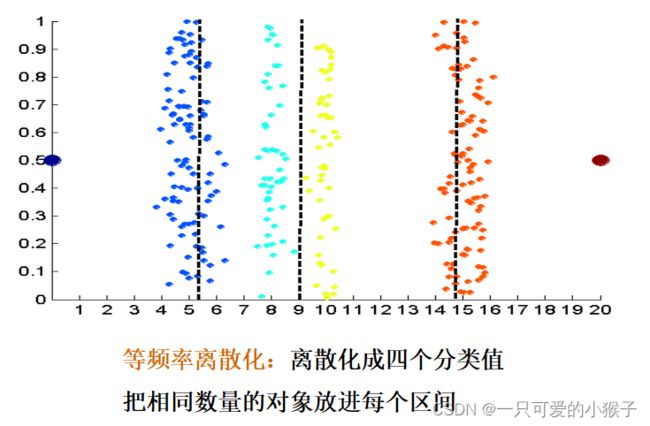
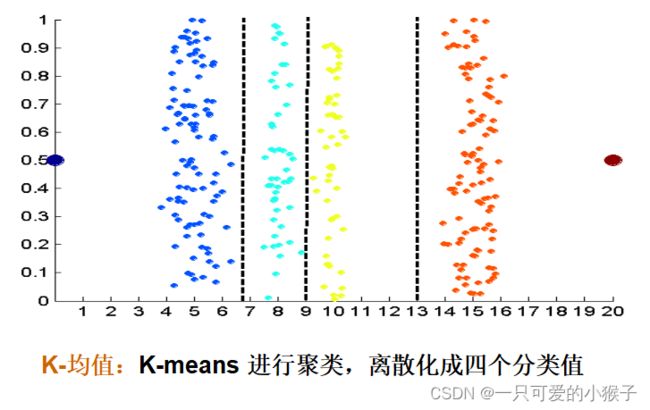
监督离散化: 使用类标签查找间断点，新的样本就能依据此离散化，再分类

采样

采样以降低数据读取处理的时间复杂度
抽样可以用来调整类的分布（应用于不平衡数据集）

什么是不平衡数据集？

不平衡数据集是指在解决分类问题时每个类别的样本量不均衡的数据集。

不平衡数据集会产生什么弊端？

下面这个例子：100个人其中99都是健康的，一个人得了癌症。通过这个不平衡数据集训练一个分类器，不管预测的人是否都是健康的，准确率都有99%，这个不平衡数据集训练出的模型没有意义。
这就是不平衡数据集的弊端。

如何规避不平衡数据集产生的弊端？

（1）通过抽样来调整类的分布
  对小类样本进行采样来增加小类样本的数量—过采样(增加部分样本的副本)
  对大类样本进行采样来增加小类样本的数量—欠采样（删除部分样本)
          

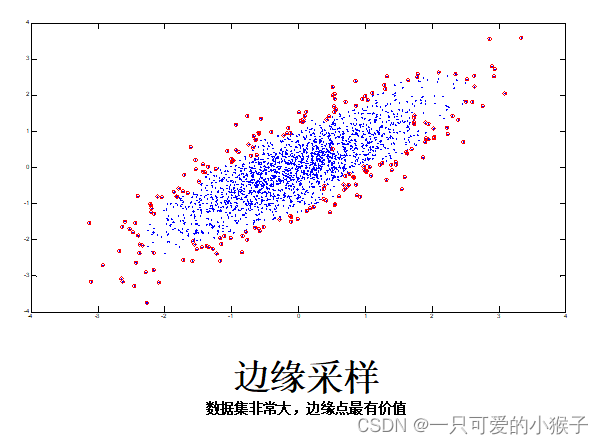
（2）定义新的准确率的评价标注

数据标准化

有明确上下界：Min-max 标准化

无上下界：Z-score标准化

数据统计描述和可视化

数据描述的统计量

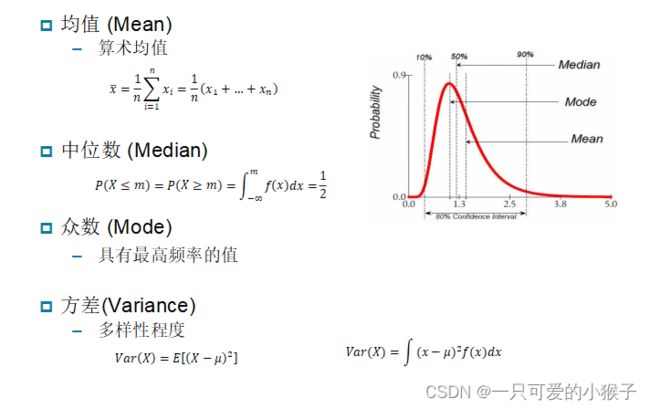
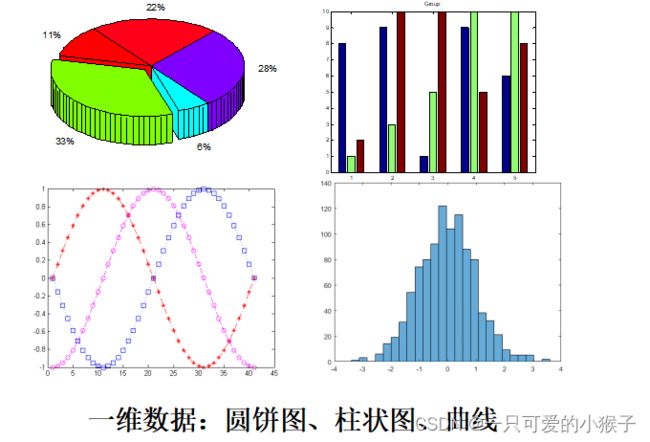
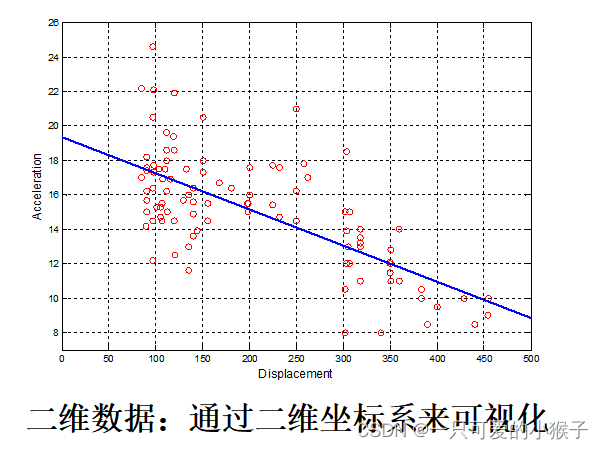
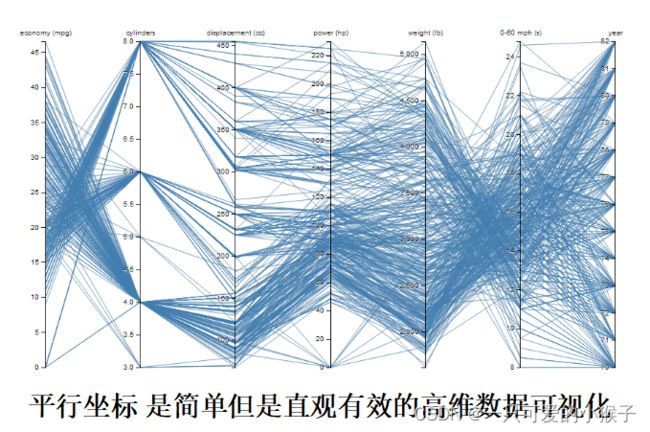
数据可视化

数据的选择与提取

为什么要特征提取？

属性太多会造成整个空间的维度太大（可能会引发维度灾难），比如说在100维做分类，就需要在100维的特空间上寻找决策边界，这会造成问题的难度太大。
因此需要特征提取，挑出最相关的属性，把问题的难度降低。

如何判断属性的好坏？

定性：类别柱状图（离散型属性）、类别分布图（连续型属性）
定量：熵、信息增益
熵用于衡量一个系统的不确定性。也就是衡量一个值取多少或者判断一个类是什么时的置信度。信息量的数学期望，在信息论中衡量一个系统的不确定性。(越小越好)
信息增益：当知道额外属性时，对整个系统的不确定性降低了多少。(越大越好)