机器学习(11)——时间序列分析
目录
1 时间序列数据的相关检验
1.1 白噪声检验
1.2 平稳性检验
1.3 自相关分析和偏自相关分析
2 移动平均算法
2.1 简单移动平均法
2.2 简单指数平滑法
2.3 霍尔特线性趋势法
2.4 Holt-Winters 季节性预测模型
3 ARIMA 模型
3.1 AR 模型
3.2 ARMA 模型
3.3 ARIMA 模型
3.3.1 训练ARIMA模型
3.3.2自动搜索ARIMA模型的参数
4 SARIMA 模型
5 Prophet 模型预测时间序列
5.1 数据准备
5.2 模型建立与数据预测
6 多元时间序列ARIMAX模型
6.1 数据准备与可视化
6.2 ARIMAX模型建立与预测
7 时序数据的异常值检测
7.1 数据准备与可视化
7.2 时序数据异常值检测
时间序列数据是常见的数据类型之一,时间序列分析基于随机过程理论和数理统计学方法,研究时间序列数据所遵从的统计规律,常用于系统描述、系统分析、预测未来等。
时间序列数据主要是根据时间先后,对同样的对象按照等时间间隔收集的数据,比如每日的平均气温、每天的销售额、每月的降水量等。虽然有些序列所描述的内容取值是连续的,比如气温的变化可能是连续的,但是由于观察的时间段并不是连续的,所以可以认为是离散的时间序列数据。
一般地,对任何变量做定期记录就能构成一个时间序列。根据所研究序列数量的不同,可以将时间序列数据分为一元时间序列数据和多元时间序列数据。
时间序列的变化可能受一个或多个因素的影响,导致它在不同时间的取值有差异,这些影响因素分别是长期趋势、季节变动、循环波动(周期波动)和不规则波动(随机波动)。时间序列分析主要有确定性变化分析和随机性变化分析。确定性变化分析包括趋势变化分析、周期变化分析、循环变化分析。随机性变化分析主要有AR、MA、ARMA、ARIMA模型等。
首先导入本章会使用到的库和模块,程序如下:
## 图像显示中文的问题
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
import seaborn as sns
sns.set(font= "Kaiti",style="ticks",font_scale=1.4)
## 导入会使用到的相关库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import *
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.tsa.api import SimpleExpSmoothing,Holt,ExponentialSmoothing,AR,ARIMA,ARMA
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import pmdarima as pm
from sklearn.metrics import mean_absolute_error
import pyflux as pf
from fbprophet import Prophet
## 忽略提醒
import warnings
warnings.filterwarnings("ignore")时间序列模型的预测主要可以通过statsmodels 库的tsa模块来完成。针对时间序列数据,常用的分析流程如下:
(1)根据时间序列的散点图、自相关函数和偏自相关函数图等识别序列是否是非随机序列,如果是非随机序列,则观察其平稳性。
(2)对非平稳的时间序列数据采用差分进行平稳化处理,直到处理后序列是平稳的非随机序列。
(3)根据所识别出来的特征建立相应的时间序列模型。
(4)参数估计,检验是否具有统计意义。
(5)假设检验,判断模型的残差序列是否为白噪声序列。
(6)利用已通过检验的模型进行预测。
1 时间序列数据的相关检验
对于时间序列数据,最重要的检验就是时间序列数据是否为白噪声数据、时间序列数据是否平稳,以及对时间序列数据的自相关系数和偏自相关系数进行分析。如果时间序列数据是白噪声数据, 说明其没有任何有用的信息。针对时间序列数据的很多分析方法,都要求所研究的时间序列数据是平稳的,所以判断时间序列数据是否平稳,以及如何将非平稳的时间序列数据转化为平稳序列数据,对时间序列数据的建模研究是非常重要的。
1.1 白噪声检验
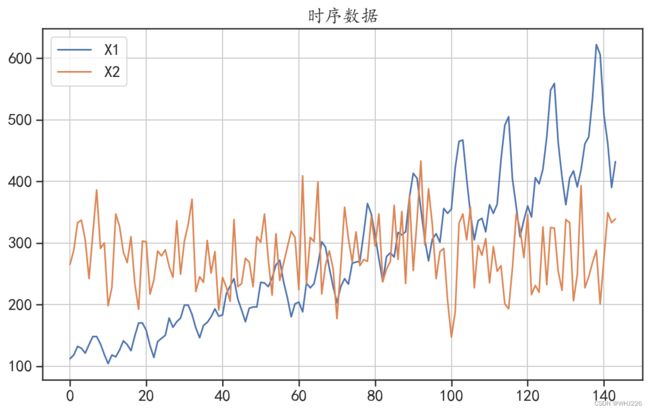
本节将会利用两个时间序列数据进行相关的检验分析,首先读取数据并使用折线图将两组时间序列进行可视化,运行下面的程序后,结果如图6-1所示。
文件提取:
链接:https://pan.baidu.com/s/1EJEOq_FuJpf2y2Rw-lcC5g
提取码:whj6
## 读取时间序列数据,该数据包含:X1为飞机乘客数据,X2为一组随机数据
df = pd.read_csv("E:/PYTHON/timeserise.csv")
## 查看数据的变化趋势
df.plot(kind = "line",figsize = (10,6))
plt.grid()
plt.title("时序数据")
plt.show()运行结果如下:
图6-1 序列的波动情况
如果一个序列是白噪声(即独立同分布的随机数据),那么就无须再对其建立时间序列模型来预测,因为预测随机数是无意义的。因此在建立时间序列分析之前,需要先对其进行白噪声检验。
常用的白噪声检验方法是Ljung-Box检验(简称LB检验),其原假设和备择假设分别为HO:延迟期数小于或等于m期的序列之间相互独立(序列是白噪声); H1:延迟期数小于或等于m期的序列之间有相关性(序列不是白噪声)。 Ljung-Box 检验可以使用 sm.stats.diagnostic.acorr_ljungbox()函数,对两个序列进行白噪声检验,程序如下:
## 白噪声检验Ljung-Box检验
## 该检验用来检查序列是否为随机序列,如果是随机序列,那它们的值之间没有任何关系
## 使用LB检验来检验序列是否为白噪声,原假设为在延迟期数内序列之间相互独立。
lags = [4,8,16,32]
LB = sm.stats.diagnostic.acorr_ljungbox(df["X1"],lags = lags,return_df = True)
print("序列X1的检验结果:\n",LB)
LB = sm.stats.diagnostic.acorr_ljungbox(df["X2"],lags = lags,return_df = True)
print("序列X2的检验结果:\n",LB)
## 如果P值小于0.05,说明序列之间不独立,不是白噪声运行结果如下:
序列X1的检验结果:
lb_stat lb_pvalue
4 427.738684 2.817731e-91
8 709.484498 6.496271e-148
16 1289.037076 1.137910e-264
32 1792.523003 0.000000e+00
序列X2的检验结果:
lb_stat lb_pvalue
4 1.822771 0.768314
8 8.452830 0.390531
16 15.508599 0.487750
32 28.717743 0.633459从上面的结果中可以看出,在延迟阶数为[4,8,16,32]的情况下,序列X1的LB检验P值均小于0.05,说明可以拒绝序列为白噪声的原假设,认为该数据不是随机数据,即该数据不是随机的,是有规律可循的,有分析价值。而序列X2的LB检验P值均大于0.05,说明该序列为白噪声,没有分析价值。
1.2 平稳性检验
时间序列是否是平稳的,对选择预测的数学模型非常关键。如果一组时间序列数据是平稳的, 就可以直接使用自回归移动平均模型(ARMA)进行预测,如果数据是不平稳的,就需要尝试建立差分移动自回归平均模型(ARIMA)等进行预测。
判断序列是否平稳有两种检验方法:一种是根据时序图和自相关图显示的特征做出判断;另一种是构造检验统计量进行假设检验,如单位根检验。第一种判断方法比较主观,第二种方法则是客观的判断方法。
常用的单位根检验方法是ADF检验,它能够检验时间序列中单位根的存在性,其检验的原假设和备择假设分别为HO:序列是非平稳的(序列有单位根); H1:序列是平稳的(序列没有单位根)。
Python中sm.tsa模块的adfuller()函数可以进行单位根检验,针对序列X1和X2可以使用下面的程序进行单位根检验。
## 序列的单位根检验,即检验序列的平稳性
dftest = adfuller(df["X2"],autolag='BIC')
dfoutput = pd.Series(dftest[0:4], index=['adf','p-value','usedlag','Number of Observations Used'])
print("X2单位根检验结果:\n",dfoutput)
dftest = adfuller(df["X1"],autolag='BIC')
dfoutput = pd.Series(dftest[0:4], index=['adf','p-value','usedlag','Number of Observations Used'])
print("X1单位根检验结果:\n",dfoutput)
## 对X1进行一阶差分后的序列进行检验
X1diff = df["X1"].diff().dropna()
dftest = adfuller(X1diff,autolag='BIC')
dfoutput = pd.Series(dftest[0:4], index=['adf','p-value','usedlag','Number of Observations Used'])
print("X1一阶差分单位根检验结果:\n",dfoutput)
## 一阶差分后 P值大于0.05, 小于0.1,可以认为其是平稳的运行结果如下:
X2单位根检验结果:
adf -1.124298e+01
p-value 1.788000e-20
usedlag 0.000000e+00
Number of Observations Used 1.430000e+02
dtype: float64
X1单位根检验结果:
adf 0.815369
p-value 0.991880
usedlag 13.000000
Number of Observations Used 130.000000
dtype: float64
X1一阶差分单位根检验结果:
adf -2.829267
p-value 0.054213
usedlag 12.000000
Number of Observations Used 130.000000
dtype: float64从上面的单位根检验的输出结果中可以发现,序列X2的检验P值小于0.05,说明X2是一个平稳时间序列(注意该序列属于白噪声,白噪声序列是平稳序列)。针对序列X1的单位根检验, 可发现其P值远大于0.05,说明其实不平稳,而针对其一阶差分后的结果可以发现,一阶差分后P值大于0.05,但是小于0.1,可以认为其是平稳序列。
针对数据的平稳性检验,还可以使用KPSS检验,其原假设为检测的序列是平稳的。该检验可以使用kpss()函数来完成,使用该函数对序列进行检验的程序如下:
## KPSS检验的原假设为:序列x是平稳的。
## 对序列X2使用KPSS检验平稳性
dfkpss = kpss(df["X2"])
dfoutput = pd.Series(dfkpss[0:3], index=["kpss_stat"," p-value"," usedlag"])
print("X2 KPSS检验结果:\n",dfoutput)
## 接受序列平稳的原假设
## 对序列X1使用KPSS检验平稳性
dfkpss = kpss(df["X1"])
dfoutput = pd.Series(dfkpss[0:3], index=["kpss_stat"," p-value"," usedlag"])
print("X1 KPSS检验结果:\n",dfoutput)
## 拒绝序列平稳的原假设
## 对序列X1使用KPSS检验平稳性
dfkpss = kpss(X1diff)
dfoutput = pd.Series(dfkpss[0:3], index=["kpss_stat"," p-value"," usedlag"])
print("X1一阶差分KPSS检验结果:\n",dfoutput)
## 接受序列平稳的原假设运行结果如下:
X2 KPSS检验结果:
kpss_stat 0.087559
p-value 0.100000
usedlag 14.000000
dtype: float64
X1 KPSS检验结果:
kpss_stat 1.052175
p-value 0.010000
usedlag 14.000000
dtype: float64
X1一阶差分KPSS检验结果:
kpss_stat 0.05301
p-value 0.10000
usedlag 14.00000
dtype: float64从输出的检验结果中可以知道,序列X2是平稳序列,序列X1是不平稳序列,X1一阶差分后的序列是平稳序列。
针对时间序列ARIMA(p,d,g)模型,参数d可以通过差分次数来确定,也可以利用pm.arima模块的ndiffs()函数进行相应的检验来确定。如果对序列建立ARIMA模型可以使用下面的程序确定参数d的取值:
## 检验ARIMA模型的参数d
X1d = pm.arima.ndiffs(df["X1"], alpha=0.05, test="kpss", max_d=3)
print("使用KPSS方法对序列X1的参数d取值进行预测,d = ",X1d)
X1diffd = pm.arima.ndiffs(X1diff, alpha=0.05, test="kpss", max_d=3)
print("使用KPSS方法对序列X1一阶差分后的参数d取值进行预测,d = ",X1diffd)
X2d = pm.arima.ndiffs(df["X2"], alpha=0.05, test="kpss", max_d=3)
print("使用KPSS方法对序列X2的参数d取值进行预测,d = ",X2d)运行结果如下:
使用KPSS方法对序列X1的参数d取值进行预测,d = 1
使用KPSS方法对序列X1一阶差分后的参数d取值进行预测,d = 0
使用KPSS方法对序列X1的参数d取值进行预测,d = 0从输出的结果中可以发现,针对平稳序列获得的参数d取值为0,而针对不平稳的时间序列X1其参数d的预测结果为1。
针对时间序列SARIMA模型,还有一个季节周期平稳性参数D需要确定,同时也可以利用pm.arima模块中的nsdiffs()函数进行相应的检验来确定,使用该函数的程序示例如下:
## 检验SARIMA模型的参数季节阶数D
X1d = pm.arima.nsdiffs(df["X1"], 12, max_D=2)
print("对序列X1的季节阶数D取值进行预测,D = ",X1d)
X1diffd = pm.arima.nsdiffs(X1diff, 12, max_D=2)
print("序列X1一阶差分后的季节阶数D取值进行预测,D = ",X1diffd)运行结果如下:
对序列X1的季节阶数D取值进行预测,D = 1
序列X1一阶差分后的季节阶数D取值进行预测,D = 1从程序的输出结果中可以发现,序列X1和序列X1一阶差分后的序列,检验结果都为D=1。
1.3 自相关分析和偏自相关分析
自相关分析和偏自相关分析,是用来确定ARMA(p,q)模型中两个参数p和g的一种方法,在 确定序列为平稳的非白噪声序列后,可以通过序列的自相关系数和偏自相关系数取值的大小来分析 序列的截尾情况。
对于一个时间序列![]() ,如果样本的自相关系数ACF不等于0,直到滞后期s=q,而滞后期 s>q时ACF几乎为0,那么可以认为真实的数据生成过程是MA(q)。如果样本的偏自相关系数 PACF 不等于0,直到滞后期s=p,而滞后期s>p时PACF几乎为0,那么可以认为真实的数据生 成过程是AR(p)。更一般的情况是,根据样本的ACF 和PACF 的表现,可拟合出一个较合适的ARMA(p,g)模型。表6-1展示了如何确定模型中的参数p和q。
,如果样本的自相关系数ACF不等于0,直到滞后期s=q,而滞后期 s>q时ACF几乎为0,那么可以认为真实的数据生成过程是MA(q)。如果样本的偏自相关系数 PACF 不等于0,直到滞后期s=p,而滞后期s>p时PACF几乎为0,那么可以认为真实的数据生 成过程是AR(p)。更一般的情况是,根据样本的ACF 和PACF 的表现,可拟合出一个较合适的ARMA(p,g)模型。表6-1展示了如何确定模型中的参数p和q。
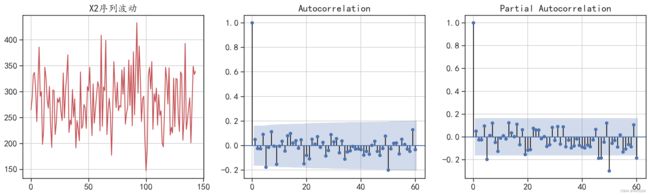
针对时间序列的自相关系数和偏自相关系数的情况,可以使用 plot_acf()函数和 plot_pacf()函 数进行可视化,运行下面的程序可获得时间序列X2的自相关系数和偏自相关系数的情况,得到的 结果如图6-2所示。
## 对随机序列X2进行自相关和偏相关分析可视化
fig = plt.figure(figsize=(16,5))
plt.subplot(1,3,1)
plt.plot(df["X2"],"r-")
plt.grid()
plt.title("X2序列波动")
ax = fig.add_subplot(1,3,2)
plot_acf(df["X2"], lags=60,ax = ax)
plt.grid()
ax = fig.add_subplot(1,3,3)
plot_pacf(df["X2"], lags=60,ax = ax)
plt.grid()
plt.tight_layout()
plt.show()
#在图像中滞后0表示自己和自己的相关性,恒等于1。不用于确定p和q。运行结果如下:
图6-2 X2的自相关系数和偏自相关系数
从图6-2中可以发现,针对白噪声的平稳序列,参数p和g的取值均可以为0。
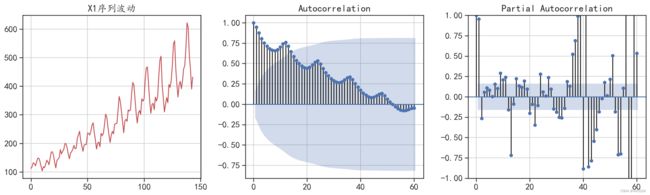
使用下面的程序可以将序列X1进行自相关分析可视化,结果如图6-3所示。
## 对非随机序列X1进行自相关和偏相关分析可视化
fig = plt.figure(figsize=(16,5))
plt.subplot(1,3,1)
plt.plot(df["X1"],"r-")
plt.grid()
plt.title("X1序列波动")
ax = fig.add_subplot(1,3,2)
plot_acf(df["X1"], lags=60,ax = ax)
plt.grid()
ax = fig.add_subplot(1,3,3)
plot_pacf(df["X1"], lags=60,ax = ax)
plt.ylim([-1,1])
plt.grid()
plt.tight_layout()
plt.show()运行结果如下:
图6-3 X1的自相关系数和偏自相关系数
从图6-3中可以发现,序列X1具有一定的周期性。
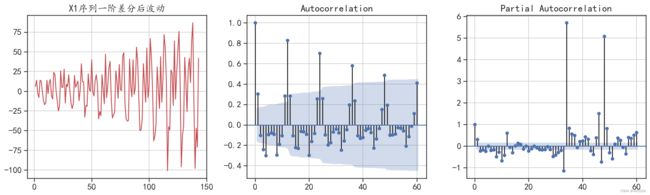
针对序列X1一阶差分后的序列,其自相关和偏自相关分析可视化可以使用下面的程序,运行后的结果如图6-4所示。
## 对非随机序列X1一阶差分后的序列进行自相关和偏相关分析可视化
fig = plt.figure(figsize=(16,5))
plt.subplot(1,3,1)
plt.plot(X1diff,"r-")
plt.grid()
plt.title("X1序列一阶差分后波动")
ax = fig.add_subplot(1,3,2)
plot_acf(X1diff, lags=60,ax = ax)
plt.grid()
ax = fig.add_subplot(1,3,3)
plot_pacf(X1diff, lags=60,ax = ax)
plt.grid()
plt.tight_layout()
plt.show()
#ARMA(p,q)中,自相关系数的滞后,对应着参数q;偏相关系数的滞后对应着参数p。运行结果如下:
图6-4 X1一阶差分后的自相关系数和偏自相关系数
从图6-4中可以发现,序列X1一阶差分后同样具有一定的周期性。
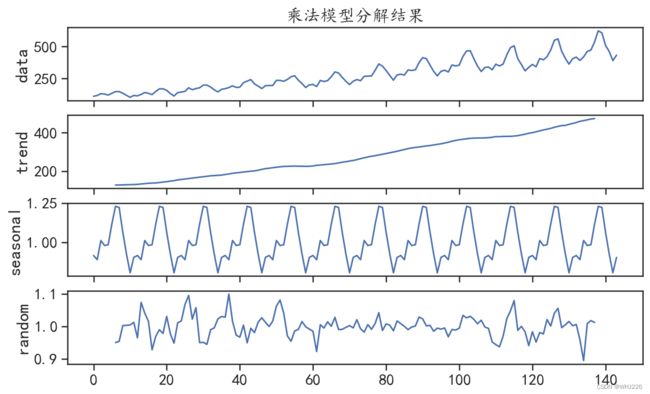
pm.arima模块的decompose()函数可以对时间序列数据进行分解,使用参数multiplicative可以获得乘法模型的分解结果,使用参数additive 可以获得加法模型的分解结果。运行下面的程序 可获得对序列X1乘法模型分解的结果,可视化结果如图6-5所示。
## 时间序列的分解
## 通过观察序列X1,可以发现其既有上升的趋势,也有周期性的趋势,所以可以将该序列进行分解
## 使用乘法模型分解结果(通常适用于有增长趋势的序列)
X1decomp = pm.arima.decompose(df["X1"].values,"multiplicative", m=12)
## 可视化出分解的结果
ax = pm.utils.decomposed_plot(X1decomp,figure_kwargs = {"figsize": (10, 6)},
show=False)
ax[0].set_title("乘法模型分解结果")
plt.show()
运行结果如下:
图6-5 序列X1的分解结果
通过观察序列X1的分解结果,可以发现其既有上升趋势,也有周期性的变化趋势
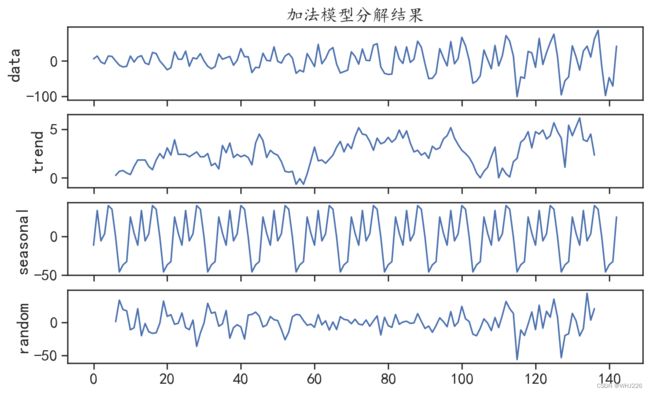
使用下面的程序可以对序列X1一阶差分后的序列使用加法模型进行分解,程序运行后的结果如图6-6所示。
## 使用加法模型分解结果(通常适用于平稳趋势的序列)
X1decomp = pm.arima.decompose(X1diff.values,"additive", m=12)
## 可视化出分解的结果
ax = pm.utils.decomposed_plot(X1decomp,figure_kwargs = {"figsize": (10, 6)},
show=False)
ax[0].set_title("加法模型分解结果")
plt.show()运行结果如下:
图6-6 序列X1一阶差分后的分解结果
2 移动平均算法
移动平均算法是一种简单有效的时间序列的预测方法,它的基本思想是:根据时间序列逐项推 移,依次计算包含一定项数的序时平均值,以反映长期趋势。该预测方法中最简单的是简单移动平 均法和简单指数平滑法,较复杂的有霍尔特线性趋势法和Holt-Winters季节性预测模型方法。
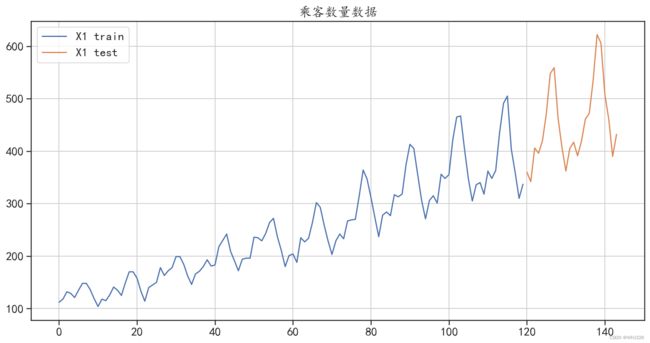
本节将使用前面导入的时间序列X1,结合多种移动平均算法对其进行建模与预测,建模时会将 数据后面的24个样本作为测试集,将前面的样本作为训练集,数据切分程序如下,程序运行后的结 果如图6-7所示。训练集中包含120个样本,测试集中包含24个样本。
## 数据准备
## 对序列X1进行切分,后面的24个数据用于测试集
train = pd.DataFrame(df["X1"][0:120])
test = pd.DataFrame(df["X1"][120:])
## 可视化切分后的数据
train["X1"].plot(figsize=(14,7), title= "乘客数量数据",label = "X1 train")
test["X1"].plot(label = "X1 test")
plt.legend()
plt.grid()
plt.show()
print(train.shape)
print(test.shape)
df["X1"].shape运行结果如下:
(120, 1)
(24, 1)
(144,)图6-7 训练集和测试集的划分
2.1 简单移动平均法
简单移动平均法中各元素的权重都相等。Python中可以使用时间序列的rolling()和mean()方法进行计算和预测,对切分后的序列进行预测的程序如下,程序中同时将训练集、测试集和预测数 据进行了可视化对比分析, rolling(24).mean()表示计算最近的24个数据的均值,作为待预测数据 的结果,程序运行后的结果如图6-8所示。
## 简单移动平均进行预测
y_hat_avg = test.copy(deep = False)
y_hat_avg["moving_avg_forecast"] = train["X1"].rolling(24).mean().iloc[-1]
## 可视化出预测结果
plt.figure(figsize=(14,7))
train["X1"].plot(figsize=(14,7),label = "X1 train")
test["X1"].plot(label = "X1 test")
y_hat_avg["moving_avg_forecast"].plot(style="g--o", lw=2,
label="移动平均预测")
plt.legend()
plt.grid()
plt.title("简单移动平均预测")
plt.show()运行结果如下:
图6-8 简单移动平均法预测的结果
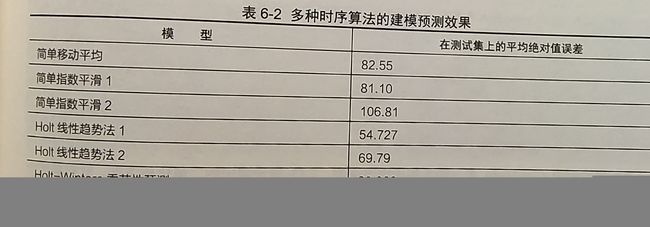
从图6-8中可以发现,使用简单移动平均法对数据进行预测的效果并不好,使用下面的程序可以计算在测试集上的平均绝对值误差,可知平均绝对值误差为82.55。
## 计算预测结果和真实值的误差
print("预测绝对值误差:",mean_absolute_error(test["X1"],y_hat_avg["moving_avg_forecast"]))运行结果如下:
预测绝对值误差: 82.552083333333362.2 简单指数平滑法
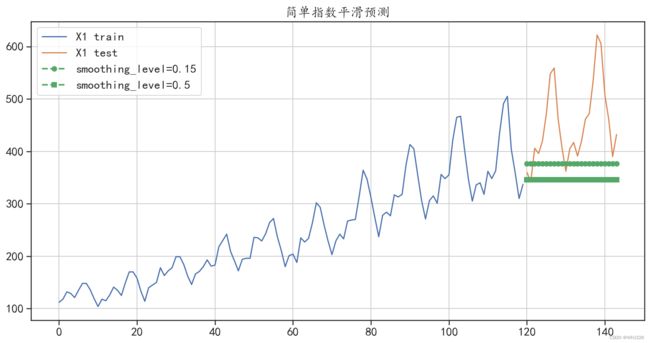
简单指数平滑又称指数移动平均值,是以指数式递减加权的移动平均。各数据的权重随时间呈 指数式递减,越近期的数据权重越大,但较旧的数据也给予一定的权重。在Python中可以使用 SimpleExpSmoothing()函数对时间序列数据进行简单指数平滑法的建模和预测,对切分后的序列 进行预测的程序如下。在下面的程序中,通过训练获得了两个指数平滑模型,分别对应着参数 smoothing_level=0.15 和 smoothing_level=0.5。同时将训练集、测试集和预测数据进行了对比 可视化,程序运行后的结果如图6-9所示。
## 数据准备
y_hat_avg = test.copy(deep = False)
## 模型构建
model1 = SimpleExpSmoothing(train["X1"].values).fit(smoothing_level=0.15)
y_hat_avg["exp_smooth_forecast1"] = model1.forecast(len(test))
model2 = SimpleExpSmoothing(train["X1"].values).fit(smoothing_level=0.5)
y_hat_avg["exp_smooth_forecast2"] = model2.forecast(len(test))
## 可视化出预测结果
plt.figure(figsize=(14,7))
train["X1"].plot(figsize=(14,7),label = "X1 train")
test["X1"].plot(label = "X1 test")
y_hat_avg["exp_smooth_forecast1"].plot(style="g--o", lw=2,
label="smoothing_level=0.15")
y_hat_avg["exp_smooth_forecast2"].plot(style="g--s", lw=2,
label="smoothing_level=0.5")
plt.legend()
plt.grid()
plt.title("简单指数平滑预测")
plt.show()
## 计算预测结果和真实值的误差
print("smoothing_level=0.15,预测绝对值误差:",
mean_absolute_error(test["X1"],y_hat_avg["exp_smooth_forecast1"]))
print("smoothing_level=0.5,预测绝对值误差:",
mean_absolute_error(test["X1"],y_hat_avg["exp_smooth_forecast2"]))运行结果如下:
smoothing_level=0.15,预测绝对值误差: 81.10115706423566
smoothing_level=0.5,预测绝对值误差: 106.813228720506图6-9 简单指数平滑法预测结果
从输出结果和图6-9中可以发现,参数smoothing_level=0.15获得的模型预测效果,比参数 smoothing_level=0.5 获得的模型预测效果更好。但是使用指数平滑法获得的模型,预测效果仍然 较差。
2.3 霍尔特线性趋势法
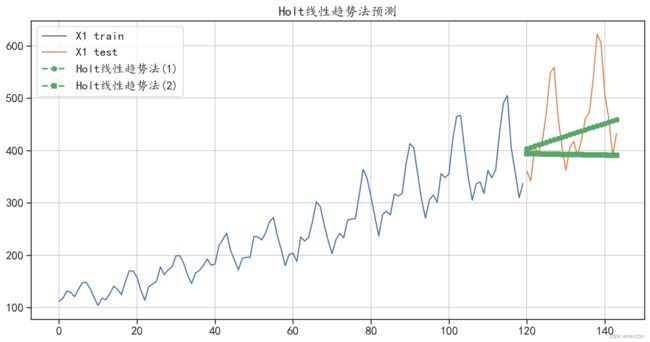
霍尔特(Holt)线性趋势法是扩展了的简单指数平滑法,其允许有趋势变化的数据预测,所以 对于有趋势变化的序列可能会获得更好的预测结果。Python中可以使用Holt()函数对时间序列进行霍尔特(Holt)线性趋势法的建模和预测,并且可以使用 smoothing_level 和 smoothing_slope 两个参数控制模型的拟合情况。对切分后的序列进行预测的程序如下,程序中分别训练获得了两个 霍尔特(Holt)线性趋势法模型,对应的参数有 smoothing_level=0.15, smoothing_slope=0.05 和smoothing_level=0.15、 smoothing_slope=0.25。程序中还将训练集、测试集和预测数据进 行了可视化,程序运行后的结果如图6-10所示。
## 数据准备
y_hat_avg = test.copy(deep = False)
## 模型构建
model1 = Holt(train["X1"].values).fit(smoothing_level=0.1,
smoothing_slope = 0.05)
y_hat_avg["holt_forecast1"] = model1.forecast(len(test))
model2 = Holt(train["X1"].values).fit(smoothing_level=0.1,
smoothing_slope = 0.25)
y_hat_avg["holt_forecast2"] = model2.forecast(len(test))
## 可视化出预测结果
plt.figure(figsize=(14,7))
train["X1"].plot(figsize=(14,7),label = "X1 train")
test["X1"].plot(label = "X1 test")
y_hat_avg["holt_forecast1"].plot(style="g--o", lw=2,
label="Holt线性趋势法(1)")
y_hat_avg["holt_forecast2"].plot(style="g--s", lw=2,
label="Holt线性趋势法(2)")
plt.legend()
plt.grid()
plt.title("Holt线性趋势法预测")
plt.show()
## 计算预测结果和真实值的误差
print("smoothing_slope = 0.05,预测绝对值误差:",
mean_absolute_error(test["X1"],y_hat_avg["holt_forecast1"]))
print("smoothing_slope = 0.25,预测绝对值误差:",
mean_absolute_error(test["X1"],y_hat_avg["holt_forecast2"]))运行结果如下:
smoothing_slope = 0.05,预测绝对值误差: 54.727467142360275
smoothing_slope = 0.25,预测绝对值误差: 69.79052992788556图6-10 霍尔特线性趋势法预测结果
从输出结果和图6-10 中可以发现,使用参数smoothing_level=0.15, smoothing_ slope=0.05获得的模型预测效果更好,而且两个霍尔特线性趋势法模型的预测效果均比移动平均法 的效果更好。
2.4 Holt-Winters 季节性预测模型
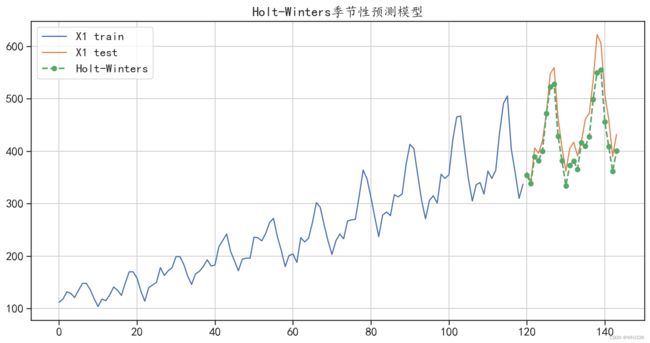
Holt-Winters 季节性预测模型又称为三次指数平滑法,其可以对带有季节周期性和线性趋势的 数据进行更好的预测和建模,是对霍尔特(Holt)线性趋势法的进一步扩展。Python中可以使用 ExponentialSmoothing()函数对时间序列进行建模和预测,并且可以使用 seasonal_periods 参数 指定数据的季节周期性,从而控制模型的拟合情况。对切分后的序列进行预测的程序如下,程序中 训练获得了Holt-Winters季节性预测模型,同时在程序中将训练集、测试集和预测数据进行了对比可视化,程序运行后的结果如图6-11所示。
## 数据准备
y_hat_avg = test.copy(deep = False)
## 模型构建
model1 = ExponentialSmoothing(train["X1"].values,
seasonal_periods=12, # 周期性为12
trend="add", seasonal="add").fit()
y_hat_avg["holt_winter_forecast1"] = model1.forecast(len(test))
## 可视化出预测结果
plt.figure(figsize=(14,7))
train["X1"].plot(figsize=(14,7),label = "X1 train")
test["X1"].plot(label = "X1 test")
y_hat_avg["holt_winter_forecast1"].plot(style="g--o", lw=2,
label="Holt-Winters")
plt.legend()
plt.grid()
plt.title("Holt-Winters季节性预测模型")
plt.show()
## 计算预测结果和真实值的误差
print("Holt-Winters季节性预测模型,预测绝对值误差:",
mean_absolute_error(test["X1"],y_hat_avg["holt_winter_forecast1"]))运行结果如下:
Holt-Winters季节性预测模型,预测绝对值误差: 30.06821059070873图6-11 Holt-Winters季节性预测模型预测结果
从输出结果和图6-11中可以发现,Holt-Winters季节性预测模型的预测效果很好地预测了序 列的周期性趋势和线性增长趋势,在测试集上的平均绝对值误差为30.068,是介绍的几个模型中预 测效果最好的模型。
3 ARIMA 模型
差分自回归移动平均模型(Auto-Regressive Integrated Moving Average, ARIMA )是差 分运算与ARMA模型的组合,即任何非平稳序列如果能够通过适当阶数的差分实现平稳,就可以对 差分后的序列拟合ARMA模型。ARMA模型主要针对的是平稳的一元时间序列。本节将分别介绍 使用AR 模型、ARMA 模型和ARIMA 模型对前面的时间序列X1进行拟合时的情况,对比分析不 同模型所获得的拟合效果。
3.1 AR 模型
使用 AR 模型对时间序列X1进行预测时,经过前面序列的偏自相关系数的可视化结果,使用 AR(2)模型可对序列进行建模,使用ARMA()函数进行建模的程序如下。注意在该函数中参数 order=(2,0),表示使用 AR(2)模型对数据进行训练。
## 注意针对乘客数据X1,使用AR模型或者ARMA模型进行预测,并不是非常的合适,
## 这里是使用AR和ARMA模型进行预测的目的主要是为了和更好的模型预测结果进行对比
## 使用AR模型对乘客数据进行预测
## 经过前面序列的偏相关系数的可视化结果,使用AR(2)模型可对序列进行建模
## 数据准备
y_hat = test.copy(deep = False)
## 模型构建
ar_model = ARMA(train["X1"].values,order = (2,0)).fit()
## 输出拟合模型的结果
print(ar_model.summary())
## AIC=1141.989;BIC= 1153.138;两个系数是显著的运行结果如下:
ARMA Model Results
==============================================================================
Dep. Variable: y No. Observations: 120
Model: ARMA(2, 0) Log Likelihood -566.994
Method: css-mle S.D. of innovations 26.976
Date: Thu, 23 Jul 2020 AIC 1141.989
Time: 16:05:02 BIC 1153.138
Sample: 0 HQIC 1146.517
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 243.4434 39.119 6.223 0.000 166.771 320.116
ar.L1.y 1.2573 0.086 14.568 0.000 1.088 1.426
ar.L2.y -0.3152 0.087 -3.623 0.000 -0.486 -0.145
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.0973 +0.0000j 1.0973 0.0000
AR.2 2.8911 +0.0000j 2.8911 0.0000
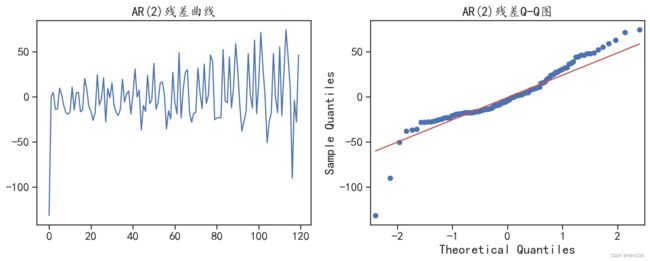
-----------------------------------------------------------------------------从模型的输出结果中可以发现,AR(2)模型的AIC=1141.989、BIC=1153.138,并且两个系 数均是显著的。针对AR(2)模型使用训练集的训练结果,可以对其拟合残差的情况进行可视化分析。
下面的程序可视化出了拟合残差的变化情况和残差正态性检验 Q-Q图,程序运行后的结果如图 6-12所示。
## 查看模型的拟合残差分布
fig = plt.figure(figsize=(12,5))
ax = fig.add_subplot(1,2,1)
plt.plot(ar_model.resid)
plt.title("AR(2)残差曲线")
## 检查残差是否符合正太分布
ax = fig.add_subplot(1,2,2)
sm.qqplot(ar_model.resid, line='q', ax=ax)
plt.title("AR(2)残差Q-Q图")
plt.tight_layout()
plt.show()运行结果如下:
图 6-12 残差的分布情况
从图6-12中可以发现,拟合残差的分布不是正态分布,说明并没有将数据中的有效信息充分 发掘。针对该AR(2)模型对测试集的预测情况,可以使用下面程序进行可视化,程序运行后的结果如图6-13所示。
## 预测未来24个数据,并输出95%置信区间
pre, se, conf = ar_model.forecast(24, alpha=0.05)
## 整理数据
y_hat["ar2_pre"] = pre
y_hat["ar2_pre_lower"] = conf[:,0]
y_hat["ar2_pre_upper"] = conf[:,1]
## 可视化出预测结果
plt.figure(figsize=(14,7))
train["X1"].plot(figsize=(14,7),label = "X1 train")
test["X1"].plot(label = "X1 test")
y_hat["ar2_pre"].plot(style="g--o", lw=2,label="AR(2)")
## 可视化出置信区间
plt.fill_between(y_hat.index, y_hat["ar2_pre_lower"],
y_hat["ar2_pre_upper"],color='k',alpha=.15,
label = "95%置信区间")
plt.legend()
plt.grid()
plt.title("AR(2)模型")
plt.show()
# 计算预测结果和真实值的误差
print("AR(2)模型预测的绝对值误差:",
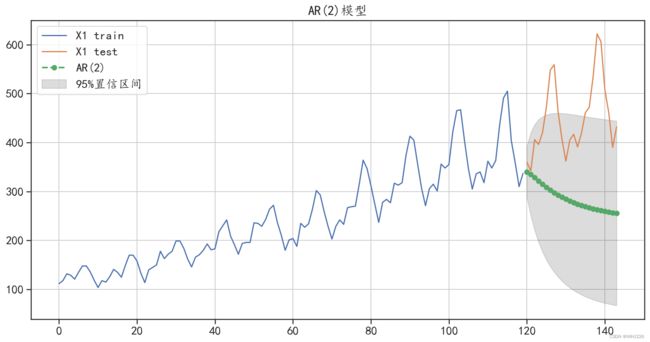
mean_absolute_error(test["X1"],y_hat["ar2_pre"]))运行结果如下:
AR(2)模型预测的绝对值误差: 165.79608244918572图6-13 AR(2)预测结果可视化
从图6-13 中可以发现,AR(2)模型对测试集的预测,完全没有获取数据的趋势,受到了数据 中部分数据值下降的影响,同时从预测误差中,也可以发现模型对数据的预测效果不好。
3.2 ARMA 模型
前面使用的AR(2)模型并没有很好地拟合数据的变化趋势,因此这里尝试使用ARMA模型对其 进行建模预测,根据前面的自相关系数和偏自相关系数分析,为了降低模型的复杂度,可以建立 ARMA(2,1)模型。使用训练集拟合模型的程序如下:
## 尝试使用ARMA模型进行预测
## 根据前面的自相关系数和偏相关系数,为了降低模型的复杂读,可以使用ARMA(2,1)
## 数据准备
y_hat = test.copy(deep = False)
## 模型构建
arma_model = ARMA(train["X1"].values,order = (2,1)).fit()
## 输出拟合模型的结果
print(arma_model.summary())
## AIC=1141.989;BIC= 1153.138;两个系数是显著的运行结果如下:
ARMA Model Results
==============================================================================
Dep. Variable: y No. Observations: 120
Model: ARMA(2, 1) Log Likelihood -564.185
Method: css-mle S.D. of innovations 26.294
Date: Thu, 23 Jul 2020 AIC 1138.371
Time: 16:05:03 BIC 1152.308
Sample: 0 HQIC 1144.031
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 243.7449 46.844 5.203 0.000 151.933 335.557
ar.L1.y 0.4617 0.156 2.966 0.003 0.157 0.767
ar.L2.y 0.4539 0.155 2.933 0.003 0.151 0.757
ma.L1.y 0.8607 0.112 7.714 0.000 0.642 1.079
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.0604 +0.0000j 1.0604 0.0000
AR.2 -2.0777 +0.0000j 2.0777 0.5000
MA.1 -1.1618 +0.0000j 1.1618 0.5000
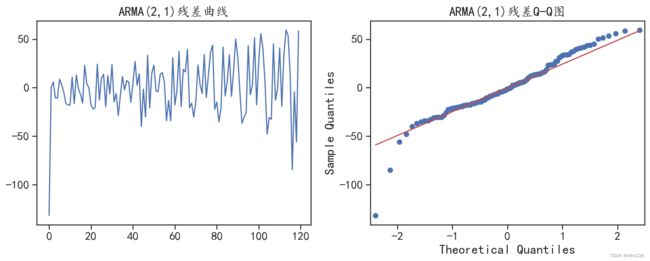
-----------------------------------------------------------------------------从模型的输出结果中可以发现,ARMA(2,1)模型的AIC=1138.371、BIC=1152.308,和AR(2) 相比拟合效果有所提升,并且3个系数均是显著的。针对ARMA(2,1)模型使用训练集训练出的结果 可以对其拟合残差的情况进行可视化分析。在下面的程序中,可视化出了拟合残差的变化情况,以 及残差正态性检验Q-Q图,程序运行后的结果如图6-14所示,
## 查看模型的拟合残差分布
fig = plt.figure(figsize=(12,5))
ax = fig.add_subplot(1,2,1)
plt.plot(arma_model.resid)
plt.title("ARMA(2,1)残差曲线")
## 检查残差是否符合正太分布
ax = fig.add_subplot(1,2,2)
sm.qqplot(arma_model.resid, line='q', ax=ax)
plt.title("ARMA(2,1)残差Q-Q图")
plt.tight_layout()
plt.show()运行结果如下:
图6-14 ARM模型的残差分布情况
从图6-14中可以发现,拟合残差的分布不是正态分布,说明使用ARMA(2,1)并没有很好地进 行数据拟合。针对该ARMA(2,1)模型对测试集的预测情况,可以使用下面的程序进行可视化,程序 运行后的结果如图6-15所示。
## 预测未来24个数据,并输出95%置信区间
pre, se, conf = arma_model.forecast(24, alpha=0.05)
## 整理数据
y_hat["arma_pre"] = pre
y_hat["arma_pre_lower"] = conf[:,0]
y_hat["arma_pre_upper"] = conf[:,1]
## 可视化出预测结果
plt.figure(figsize=(14,7))
train["X1"].plot(figsize=(14,7),label = "X1 train")
test["X1"].plot(label = "X1 test")
y_hat["arma_pre"].plot(style="g--o", lw=2,label="ARMA(2,1)")
## 可视化出置信区间
plt.fill_between(y_hat.index, y_hat["arma_pre_lower"],
y_hat["arma_pre_upper"],color='k',alpha=.15,
label = "95%置信区间")
plt.legend()
plt.grid()
plt.title("ARMA(2,1)模型")
plt.show()
# 计算预测结果和真实值的误差
print("ARMA模型预测的绝对值误差:",
mean_absolute_error(test["X1"],y_hat["arma_pre"]))运行结果如下:
ARMA模型预测的绝对值误差: 147.26531763335154图6-15 ARMA(2,1)预测结果可视化
从图6-15中可以发现,ARMA(2,1)对测试集的预测结果同样完全没有获取数据的变化趋势, 受到了数据中部分数据值下降的影响,同时从预测误差中也可以发现模型对数据的预测效果不好。
不能获得较好预测效果的原因有多个,比如:①原始数据为有周期性变化的不平稳数据,不适 合ARMA模型(注意:这里使用ARIMA系列模型对数据进行建模和预测,主要是为了和后面使用 较合适模型的预测结果做对比,在实际处理问题时可以没有这样的过程);②模型可能没有选择合 适的参数进行拟合。
这里介绍如何使用Python 中的pm.auto_arima()函数自动搜索合适的模型参数,针对ARMA 模型进行参数自动搜索的程序如下,程序运行后可以发现获得的最优模型为ARMA(3,2)。
## 自动搜索合适的参数
model = pm.auto_arima(train["X1"].values,
start_p=1, start_q=1, # p,q的开始值
max_p=12, max_q=12, # 最大的p和q
d = 0, # 寻找ARMA模型参数
m=1, # 序列的周期
seasonal=False, # 没有季节性趋势
trace=True,error_action='ignore',
suppress_warnings=True, stepwise=True)
print(model.summary())运行结果如下:
Performing stepwise search to minimize aic
Fit ARIMA(1,0,1)x(0,0,0,0) [intercept=True]; AIC=1138.852, BIC=1150.002, Time=0.083 seconds
Fit ARIMA(0,0,0)x(0,0,0,0) [intercept=True]; AIC=1436.325, BIC=1441.900, Time=0.008 seconds
Fit ARIMA(1,0,0)x(0,0,0,0) [intercept=True]; AIC=1152.396, BIC=1160.759, Time=0.039 seconds
Fit ARIMA(0,0,1)x(0,0,0,0) [intercept=True]; AIC=1295.994, BIC=1304.357, Time=0.043 seconds
Near non-invertible roots for order (0, 0, 1)(0, 0, 0, 0); setting score to inf (at least one inverse root too close to the border of the unit circle: 0.999)
Fit ARIMA(0,0,0)x(0,0,0,0) [intercept=False]; AIC=1680.279, BIC=1683.067, Time=0.006 seconds
Fit ARIMA(2,0,1)x(0,0,0,0) [intercept=True]; AIC=1138.371, BIC=1152.308, Time=0.141 seconds
Fit ARIMA(2,0,0)x(0,0,0,0) [intercept=True]; AIC=1141.989, BIC=1153.138, Time=0.070 seconds
Fit ARIMA(3,0,1)x(0,0,0,0) [intercept=True]; AIC=1138.731, BIC=1155.456, Time=0.191 seconds
Fit ARIMA(2,0,2)x(0,0,0,0) [intercept=True]; AIC=1138.677, BIC=1155.402, Time=0.206 seconds
Fit ARIMA(1,0,2)x(0,0,0,0) [intercept=True]; AIC=1140.240, BIC=1154.178, Time=0.106 seconds
Fit ARIMA(3,0,0)x(0,0,0,0) [intercept=True]; AIC=1139.932, BIC=1153.870, Time=0.117 seconds
Fit ARIMA(3,0,2)x(0,0,0,0) [intercept=True]; AIC=1137.467, BIC=1156.979, Time=0.269 seconds
Near non-invertible roots for order (3, 0, 2)(0, 0, 0, 0); setting score to inf (at least one inverse root too close to the border of the unit circle: 1.000)
Total fit time: 1.282 seconds
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 120
Model: SARIMAX(3, 0, 2) Log Likelihood -561.733
Date: Thu, 23 Jul 2020 AIC 1137.467
Time: 16:05:05 BIC 1156.979
Sample: 0 HQIC 1145.391
- 120
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 32.9054 20.908 1.574 0.116 -8.073 73.884
ar.L1 -0.0413 0.074 -0.561 0.575 -0.186 0.103
ar.L2 0.2036 0.072 2.819 0.005 0.062 0.345
ar.L3 0.7013 0.079 8.889 0.000 0.547 0.856
ma.L1 1.3215 227.530 0.006 0.995 -444.629 447.272
ma.L2 1.0000 344.340 0.003 0.998 -673.893 675.893
sigma2 637.8502 2.2e+05 0.003 0.998 -4.3e+05 4.31e+05
===================================================================================
Ljung-Box (Q): 241.15 Jarque-Bera (JB): 3.53
Prob(Q): 0.00 Prob(JB): 0.17
Heteroskedasticity (H): 6.36 Skew: -0.14
Prob(H) (two-sided): 0.00 Kurtosis: 3.79
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).针对获取的ARMA(3,2)模型,可以使用下面的程序对测试集进行预测,并对结果进行可视化分 析,程序运行后的结果如图6-16所示。
## 使用ARMA(3,2)对测试集进行预测
pre, conf = model.predict(n_periods=24, alpha=0.05,
return_conf_int=True)
## 可视化ARMA(3,2)的预测结果,整理数据
y_hat["arma_pre"] = pre
y_hat["arma_pre_lower"] = conf[:,0]
y_hat["arma_pre_upper"] = conf[:,1]
## 可视化出预测结果
plt.figure(figsize=(14,7))
train["X1"].plot(figsize=(14,7),label = "X1 train")
test["X1"].plot(label = "X1 test")
y_hat["arma_pre"].plot(style="g--o", lw=2,label="ARMA(3,2)")
## 可视化出置信区间
plt.fill_between(y_hat.index, y_hat["arma_pre_lower"],
y_hat["arma_pre_upper"],color='k',alpha=.15,
label = "95%置信区间")
plt.legend()
plt.grid()
plt.title("ARMA(3,2)模型")
plt.show()
# 计算预测结果和真实值的误差
print("ARMA模型预测的绝对值误差:",
mean_absolute_error(test["X1"],y_hat["arma_pre"]))
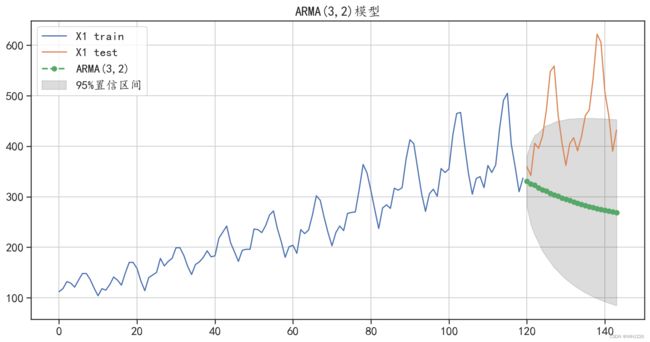
### 可以发现使用自动ARMA(3,2)模型的效果并没有ARMA(2,1)的预测效果好运行结果如下:
ARMA模型预测的绝对值误差: 158.11464180972925图6-16 ARMA(3,2)预测结果可视化
从图6-16中可以发现,ARMA(3,2)模型对测试集的预测结果同样完全没有获取数据的变化趋 势,预测效果相对于ARMA(2,1)模型并没有改善。最终发现真实原因为数据本身就不适合使用 ARMA模型进行建模和预测。
3.3 ARIMA 模型
从前面的分析中已经知道带预测的序列是不平稳的,前面使用的AR模型、ARMA模型都没有 很好地拟合数据的变化趋势,因此这里尝试使用ARIMA 模型对其进行建模预测,来应对模型的不 平稳变化趋势,根据前面的自相关系数、偏自相关系数及单位根检验结果,为了降低模型的复杂度, 可以建立ARIMA(2,1,1)模型。使用训练集拟合模型的程序如下:
## 建立ARIMA(2,1,1)模型
## 数据准备
y_hat = test.copy(deep = False)
## 模型构建
arima_model = ARIMA(train["X1"].values,order = (2,1,1)).fit()
## 输出拟合模型的结果
print(arima_model.summary())
## AIC=1099.005;BIC= 1112.900;两个系数是显著的运行结果如下:
ARIMA Model Results
==============================================================================
Dep. Variable: D.y No. Observations: 119
Model: ARIMA(2, 1, 1) Log Likelihood -544.502
Method: css-mle S.D. of innovations 23.067
Date: Thu, 23 Jul 2020 AIC 1099.005
Time: 16:05:06 BIC 1112.900
Sample: 1 HQIC 1104.647
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 2.5039 0.144 17.339 0.000 2.221 2.787
ar.L1.D.y 1.0825 0.079 13.758 0.000 0.928 1.237
ar.L2.D.y -0.5024 0.080 -6.281 0.000 -0.659 -0.346
ma.L1.D.y -0.9999 0.031 -32.736 0.000 -1.060 -0.940
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.0772 -0.9110j 1.4108 -0.1117
AR.2 1.0772 +0.9110j 1.4108 0.1117
MA.1 1.0001 +0.0000j 1.0001 0.0000
-----------------------------------------------------------------------------从ARIMA 模型的输出结果中可以发现,AIC=1099.005、BIC=1112.900,相对于前面的 ARMA 模型下降了很多,而且模型中的系数是显著的。
3.3.1 训练ARIMA模型
使用训练集训练出的ARIMA模型,可以对其拟合残差的情况进行可视化分析。在下面的程序 中,可视化出了拟合残差的变化情况,和残差正态性检验 Q-Q图,程序运行后的结果如图6-17 所示。
## 查看模型的拟合残差分布
fig = plt.figure(figsize=(12,5))
ax = fig.add_subplot(1,2,1)
plt.plot(arima_model.resid)
plt.title("ARIMA(2,1,1)残差曲线")
## 检查残差是否符合正太分布
ax = fig.add_subplot(1,2,2)
sm.qqplot(arima_model.resid, line='q', ax=ax)
plt.title("ARIMA(2,1,1)残差Q-Q图")
plt.tight_layout()
plt.show()
## 可以发现此时的残差更符合正态分布运行结果如下:
图6-17 ARIMA模型的拟合残差分布情况
从图6-17的可视化结果中可以发现,此时的残差更符合正态分布,说明模型从训练数据中获 取了更多的有用信息。
ARIMA(2,1,1)模型对测试集的预测情况,可以使用下面的程序对其进行可视化,程序运行后的 结果如图6-18所示。
## 可视化模型对测试集的预测结果
## 预测未来24个数据,并输出95%置信区间
pre, se, conf = arima_model.forecast(24, alpha=0.05)
## 整理数据
y_hat["arima_pre"] = pre
y_hat["arima_pre_lower"] = conf[:,0]
y_hat["arima_pre_upper"] = conf[:,1]
## 可视化出预测结果
plt.figure(figsize=(14,7))
train["X1"].plot(figsize=(14,7),label = "X1 train")
test["X1"].plot(label = "X1 test")
y_hat["arima_pre"].plot(style="g--o", lw=2,label="ARIMA(2,1,1)")
## 可视化出置信区间
plt.fill_between(y_hat.index, y_hat["arima_pre_lower"],
y_hat["arima_pre_upper"],color='k',alpha=.15,
label = "95%置信区间")
plt.legend()
plt.grid()
plt.title("ARIMA(2,1,1)模型")
plt.show()
# 计算预测结果和真实值的误差
print("ARIMA模型预测的绝对值误差:",
mean_absolute_error(test["X1"],y_hat["arima_pre"]))
## 可以发现ARIMA(2,1,1)很好的拟合了数据的增长趋势
运行结果如下:
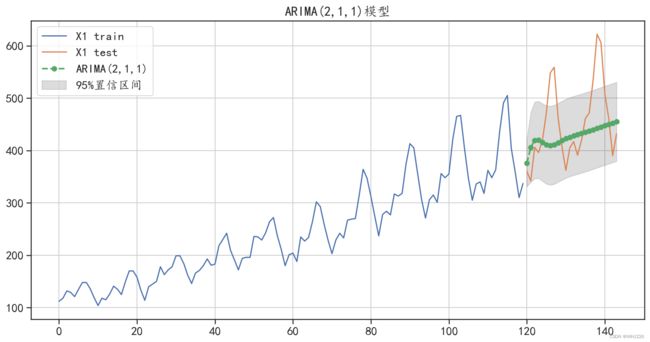
ARIMA模型预测的绝对值误差: 55.38767065734245图6-18 ARIMA(2,1,1)预测结果可视化
从图6-18中可以发现, ARIMA(2,1,1)对测试集的预测结果,很好地拟合了数据的增长趋势,但是并没有获取到数据中的周期性变化趋势。同时从预测误差中,也可以发现该模型对数据的预测 效果相对于AR 模型、ARMA模型已经有了很大的提升。
3.3.2自动搜索ARIMA模型的参数
为了获得更好的数据预测效果,同样可以使用自动参数搜索方法,使用训练数据寻找合适的模 型参数,程序如下:
## 自动搜索合适的参数的ARIMA模型
model = pm.auto_arima(train["X1"].values,
start_p=1, start_q=1, # p,q的开始值
max_p=12, max_q=12, # 最大的p和q
test="kpss", # 使用kpss检验确定d
m=1, # 序列的周期
seasonal=False, # 没有季节性趋势
trace=True,error_action='ignore',
suppress_warnings=True, stepwise=True)
print(model.summary())运行结果如下:
Performing stepwise search to minimize aic
Fit ARIMA(1,1,1)x(0,0,0,0) [intercept=True]; AIC=1126.948, BIC=1138.064, Time=0.095 seconds
Fit ARIMA(0,1,0)x(0,0,0,0) [intercept=True]; AIC=1140.292, BIC=1145.850, Time=0.012 seconds
Fit ARIMA(1,1,0)x(0,0,0,0) [intercept=True]; AIC=1132.336, BIC=1140.673, Time=0.036 seconds
Fit ARIMA(0,1,1)x(0,0,0,0) [intercept=True]; AIC=1128.668, BIC=1137.006, Time=0.071 seconds
Fit ARIMA(0,1,0)x(0,0,0,0) [intercept=False]; AIC=1138.809, BIC=1141.588, Time=0.009 seconds
Fit ARIMA(2,1,1)x(0,0,0,0) [intercept=True]; AIC=1099.003, BIC=1112.898, Time=0.207 seconds
Near non-invertible roots for order (2, 1, 1)(0, 0, 0, 0); setting score to inf (at least one inverse root too close to the border of the unit circle: 1.000)
Fit ARIMA(1,1,2)x(0,0,0,0) [intercept=True]; AIC=1106.793, BIC=1120.689, Time=0.104 seconds
Near non-invertible roots for order (1, 1, 2)(0, 0, 0, 0); setting score to inf (at least one inverse root too close to the border of the unit circle: 0.997)
Fit ARIMA(0,1,2)x(0,0,0,0) [intercept=True]; AIC=1128.350, BIC=1139.467, Time=0.070 seconds
Fit ARIMA(2,1,0)x(0,0,0,0) [intercept=True]; AIC=1128.337, BIC=1139.454, Time=0.056 seconds
Fit ARIMA(2,1,2)x(0,0,0,0) [intercept=True]; AIC=1087.029, BIC=1103.704, Time=0.247 seconds
Fit ARIMA(3,1,2)x(0,0,0,0) [intercept=True]; AIC=1098.623, BIC=1118.077, Time=0.305 seconds
Near non-invertible roots for order (3, 1, 2)(0, 0, 0, 0); setting score to inf (at least one inverse root too close to the border of the unit circle: 0.998)
Fit ARIMA(2,1,3)x(0,0,0,0) [intercept=True]; AIC=1107.859, BIC=1127.313, Time=0.311 seconds
Near non-invertible roots for order (2, 1, 3)(0, 0, 0, 0); setting score to inf (at least one inverse root too close to the border of the unit circle: 0.999)
Fit ARIMA(1,1,3)x(0,0,0,0) [intercept=True]; AIC=1108.396, BIC=1125.071, Time=0.153 seconds
Near non-invertible roots for order (1, 1, 3)(0, 0, 0, 0); setting score to inf (at least one inverse root too close to the border of the unit circle: 0.999)
Fit ARIMA(3,1,1)x(0,0,0,0) [intercept=True]; AIC=1099.799, BIC=1116.474, Time=0.261 seconds
Near non-invertible roots for order (3, 1, 1)(0, 0, 0, 0); setting score to inf (at least one inverse root too close to the border of the unit circle: 1.000)
Fit ARIMA(3,1,3)x(0,0,0,0) [intercept=True]; AIC=1084.327, BIC=1106.560, Time=0.393 seconds
Near non-invertible roots for order (3, 1, 3)(0, 0, 0, 0); setting score to inf (at least one inverse root too close to the border of the unit circle: 1.000)
Total fit time: 2.340 seconds
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 120
Model: SARIMAX(3, 1, 3) Log Likelihood -534.164
Date: Thu, 23 Jul 2020 AIC 1084.327
Time: 16:05:09 BIC 1106.560
Sample: 0 HQIC 1093.355
- 120
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 1.0449 0.389 2.687 0.007 0.283 1.807
ar.L1 0.8257 0.097 8.512 0.000 0.636 1.016
ar.L2 0.4215 0.141 2.999 0.003 0.146 0.697
ar.L3 -0.7177 0.085 -8.452 0.000 -0.884 -0.551
ma.L1 -0.8924 50.140 -0.018 0.986 -99.166 97.381
ma.L2 -0.9055 94.875 -0.010 0.992 -186.858 185.047
ma.L3 0.9869 49.471 0.020 0.984 -95.974 97.948
sigma2 428.8015 2.15e+04 0.020 0.984 -4.17e+04 4.25e+04
===================================================================================
Ljung-Box (Q): 225.53 Jarque-Bera (JB): 0.07
Prob(Q): 0.00 Prob(JB): 0.97
Heteroskedasticity (H): 6.00 Skew: 0.06
Prob(H) (two-sided): 0.00 Kurtosis: 2.96
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).最好的模型为ARIMA(3,1,3)x(0,0,0,0),即ARIMA(3,1,3)
运行程序后可以发现,找到的最好的ARIMA模型为ARIMA(3,1,3),该模型对测试集的预测情况可以使用下面的程序进行可视化,程序运行后的结果如图6-19所示。
## 可视化自动搜索参数获得的ARIMA(3,1,3)对测试集进行预测
pre, conf = model.predict(n_periods=24, alpha=0.05,
return_conf_int=True)
## 可视化ARIMA(3,1,3)的预测结果,整理数据
y_hat = test.copy(deep = False)
y_hat["arma_pre"] = pre
y_hat["arma_pre_lower"] = conf[:,0]
y_hat["arma_pre_upper"] = conf[:,1]
## 可视化出预测结果
plt.figure(figsize=(14,7))
train["X1"].plot(figsize=(14,7),label = "X1 train")
test["X1"].plot(label = "X1 test")
y_hat["arma_pre"].plot(style="g--o", lw=2,label="ARIMA(3,1,3)")
## 可视化出置信区间
plt.fill_between(y_hat.index, y_hat["arma_pre_lower"],
y_hat["arma_pre_upper"],color='k',alpha=.15,
label = "95%置信区间")
plt.legend()
plt.grid()
plt.title("ARIMA(3,1,3)模型")
plt.show()
# 计算预测结果和真实值的误差
print("ARMA模型预测的绝对值误差:",
mean_absolute_error(test["X1"],y_hat["arma_pre"]))
## 可以发现模型的预测效果比人工确定参数的ARIMA模型效果更好一些运行结果如下:
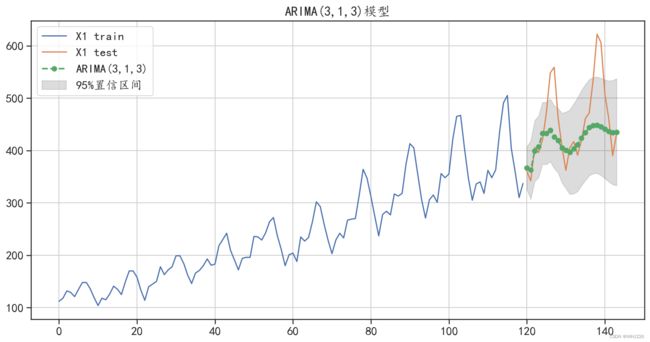
ARMA模型预测的绝对值误差: 45.31232180929982
图6-19 ARIMA(3,1,3)预测结果可视化
从图6-19中可以发现,与ARIMA(2,1,1)的测试结果相比,ARIMA(3,1,3)更好地对测试集进 行了预测,不仅获取了数据中的增长趋势,还获取了一些数据中的周期性变化信息,同时从预测误 差中也可以发现,该模型对数据的预测效果相对于AR模型、ARMA模型有了更大的提升。
但是从上面的分析中还可以发现,ARIMA模型还是不能很好地对序列X1进行建模和预测,需 要使用SARIMA模型对其进行预测分析。
4 SARIMA 模型
SARIMA 模型也称为季节ARIMA模型,本质是把一个时间序列模型通过ARIMA(p,d,g)中的 3个参数来决定,其中p代表自相关(AR)的阶数,d代表差分的阶数, g代表滑动平均(MA) 的阶数,然后加上季节性的调整。根据季节效应的相关特性,SARIMA模型可以分为简单SARIMA 模型和乘积 SARIMA模型。本节将借助SARIMA模型对时间序列X1进行建模和预测。
下面的程序可以自动搜索合适的参数,使用训练集拟合SARIMA模型。运行程序后可以发现, 获得的最优拟合模型为SARIMA(2,0,0)x(0,1,0,12),其中12表示模型的周期性。
## 使用可以拟合周期性的SARIMA模型进行建模
## 针对模型自动寻找合适的参数
model = pm.auto_arima(train["X1"].values,
start_p=1, start_q=1, # p,q的开始值
max_p=12, max_q=12, # 最大的p和q
test="kpss", # 使用kpss检验确定d
d = None, # 自动选择合适的d
m=12, # 序列的周期
seasonal=True, # 有季节性趋势
start_P = 0,start_Q = 0, # P,Q的开始值
max_P=5, max_Q=5, # 最大的P和Q
D = None, # 自动选择合适的D
trace=True,error_action='ignore',
suppress_warnings=True, stepwise=True)
print(model.summary())
## 找到的最合适的模型为 SARIMA(3,0,1)x(0,1,0,12)运行结果如下:
Performing stepwise search to minimize aic
Fit ARIMA(1,0,1)x(0,1,0,12) [intercept=True]; AIC=809.448, BIC=820.177, Time=0.106 seconds
Fit ARIMA(0,0,0)x(0,1,0,12) [intercept=True]; AIC=910.236, BIC=915.601, Time=0.018 seconds
Fit ARIMA(1,0,0)x(1,1,0,12) [intercept=True]; AIC=810.646, BIC=821.375, Time=0.309 seconds
Fit ARIMA(0,0,1)x(0,1,1,12) [intercept=True]; AIC=860.575, BIC=871.304, Time=0.205 seconds
Fit ARIMA(0,0,0)x(0,1,0,12) [intercept=False]; AIC=1060.479, BIC=1063.161, Time=0.016 seconds
Fit ARIMA(1,0,1)x(1,1,0,12) [intercept=True]; AIC=810.998, BIC=824.409, Time=0.364 seconds
Fit ARIMA(1,0,1)x(0,1,1,12) [intercept=True]; AIC=811.075, BIC=824.485, Time=0.261 seconds
Fit ARIMA(1,0,1)x(1,1,1,12) [intercept=True]; AIC=812.285, BIC=828.378, Time=0.706 seconds
Fit ARIMA(0,0,1)x(0,1,0,12) [intercept=True]; AIC=859.115, BIC=867.161, Time=0.058 seconds
Fit ARIMA(1,0,0)x(0,1,0,12) [intercept=True]; AIC=809.411, BIC=817.458, Time=0.064 seconds
Fit ARIMA(1,0,0)x(0,1,1,12) [intercept=True]; AIC=810.721, BIC=821.449, Time=0.189 seconds
Fit ARIMA(1,0,0)x(1,1,1,12) [intercept=True]; AIC=812.509, BIC=825.920, Time=0.575 seconds
Fit ARIMA(2,0,0)x(0,1,0,12) [intercept=True]; AIC=808.863, BIC=819.592, Time=0.074 seconds
Fit ARIMA(2,0,0)x(1,1,0,12) [intercept=True]; AIC=810.482, BIC=823.892, Time=0.339 seconds
Fit ARIMA(2,0,0)x(0,1,1,12) [intercept=True]; AIC=810.553, BIC=823.964, Time=0.218 seconds
Fit ARIMA(2,0,0)x(1,1,1,12) [intercept=True]; AIC=811.605, BIC=827.697, Time=0.635 seconds
Near non-invertible roots for order (2, 0, 0)(1, 1, 1, 12); setting score to inf (at least one inverse root too close to the border of the unit circle: 0.991)
Fit ARIMA(3,0,0)x(0,1,0,12) [intercept=True]; AIC=809.375, BIC=822.785, Time=0.124 seconds
Fit ARIMA(2,0,1)x(0,1,0,12) [intercept=True]; AIC=809.672, BIC=823.082, Time=0.132 seconds
Fit ARIMA(3,0,1)x(0,1,0,12) [intercept=True]; AIC=811.251, BIC=827.344, Time=0.222 seconds
Total fit time: 4.639 seconds
SARIMAX Results
==========================================================================================
Dep. Variable: y No. Observations: 120
Model: SARIMAX(2, 0, 0)x(0, 1, 0, 12) Log Likelihood -400.431
Date: Thu, 23 Jul 2020 AIC 808.863
Time: 16:05:14 BIC 819.592
Sample: 0 HQIC 813.213
- 120
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 4.2859 2.035 2.106 0.035 0.297 8.275
ar.L1 0.6783 0.100 6.816 0.000 0.483 0.873
ar.L2 0.1550 0.096 1.609 0.108 -0.034 0.344
sigma2 96.2826 11.855 8.121 0.000 73.046 119.519
===================================================================================
Ljung-Box (Q): 41.99 Jarque-Bera (JB): 1.64
Prob(Q): 0.38 Prob(JB): 0.44
Heteroskedasticity (H): 1.41 Skew: 0.02
Prob(H) (two-sided): 0.31 Kurtosis: 3.60
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).使用训练数据获得的最优模型SARIMA(3,0,1)x(0,1,0,12),对测试集进行预测,预测情况可 以使用下面的程序进行可视化,程序运行后的结果如图6-20所示。
## 可视化自动搜索参数获得的SARIMA(2, 0, 0)x(0, 1, 0, 12)对测试集进行预测
pre, conf = model.predict(n_periods=24, alpha=0.05,
return_conf_int=True)
## 可视化SARIMAX(2, 0, 0)x(0, 1, 0, 12)的预测结果,整理数据
y_hat = test.copy(deep = False)
y_hat["sarima_pre"] = pre
y_hat["sarima_pre_lower"] = conf[:,0]
y_hat["sarima_pre_upper"] = conf[:,1]
## 可视化出预测结果
plt.figure(figsize=(14,7))
train["X1"].plot(figsize=(14,7),label = "X1 train")
test["X1"].plot(label = "X1 test")
y_hat["sarima_pre"].plot(style="g--o", lw=2,label="SARIMA")
## 可视化出置信区间
plt.fill_between(y_hat.index, y_hat["sarima_pre_lower"],
y_hat["sarima_pre_upper"],color='k',alpha=.15,
label = "95%置信区间")
plt.legend()
plt.grid()
plt.title("SARIMA(2,0,0)x(0,1,0,12)模型")
plt.show()
# 计算预测结果和真实值的误差
print("SARIMA模型预测的绝对值误差:",
mean_absolute_error(test["X1"],y_hat["sarima_pre"]))
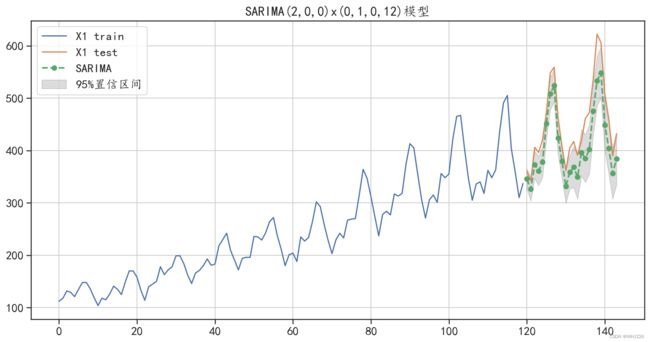
## 可以发现SARIMA模型很好的预测了算法的变化趋势,但是预测值比真实值较小,预测效果也很不错运行结果如下:
SARIMA模型预测的绝对值误差: 43.464894357672186图6-20 SARIMA(3,0,1)x(0,1,0,12)预测结果可视化
从图6-20中可以发现, SARIMA(3,0,1)x(0,1,0,12)的预测结果与ARIMA模型的预测结果相 比,预测精度有了很大的提开。SARIMA模型不仅获取了数据中的增长趋势,还准确地获取了数据 中的周期性变化信息,同时从预测的平均绝对值误差中也可以发现,该模型对数据的预测效果相对 于AR模型、ARMA模型、ARIMA模型有了更大的提升。其预测平均绝对值误差为43.46,预测 效果很好。
5 Prophet 模型预测时间序列
Prophet 模型是Facebook 发布的一款开源时序预测工具,它提供了基于Python调用的 prophet 库,该包提供的基本模型为:
y = g(t) + s(t) + h(t) +![]()
该公式将时间序列分为4个部分: g(t)为增长函数,用来表示线性或非线性的增长趋势; s(t)表 示周期性变化,变化的周期可以是年、季度、月、每天等;h(t)表示时间序列中那些潜在的具样 固定周期的节假日对预测值造成的影响;最后的![]() 为噪声项,表示随机的无法预测的波动。在Prophet 模型中,预测流程分为4个部分:模型建立、模型评估、呈现问题、可视化分析预测效果。
为噪声项,表示随机的无法预测的波动。在Prophet 模型中,预测流程分为4个部分:模型建立、模型评估、呈现问题、可视化分析预测效果。
下面将会使用一个时间序列数据介绍如何使用Prophet模型对时间序列进行建模和预测。
5.1 数据准备
Prophet 模型对时间序列进行预测时,需要的数据格式为数据表,并且包含时间变量ds和数值 变量y。下面使用Prophet模型进行时间序列的预测,使用的数据为飞机场乘客数量数据,该序列 和前面使用的序列X1相同。数据准备程序如下:
## prophet对时间序列进行预测时,需要的数据为数据表格式,并且包含时间变量ds和数值变量y
## 使用prophet模型进行时间序列的预测
## 读取数据
df = pd.read_csv("E:/PYTHON/AirPassengers.csv")
df.columns = ["ds","y"]
## 定义时间数据的数据类型
df["ds"] = pd.to_datetime(df["ds"])
print(df.head())运行结果如下:
ds y
0 1949-01-01 112
1 1949-02-01 118
2 1949-03-01 132
3 1949-04-01 129
4 1949-05-01 1215.2 模型建立与数据预测
在数据准备好后,使用前面的120个样本作为训练集,使用后面的24个样本作为测试集。可 以使用下面的程序,利用Prophet()函数建立时序数据的拟合模型 model。在建模时,参数 growth="linear"指定序列的增长趋势为线性趋势;参数 yearly.seasonality=TRUE 表示序列包含 以年为周期的季节趋势;参数weekly.seasonality=FALSE 和 daily.seasonality=FALSE 表示序 列不包含以周和天为周期的季节趋势;参数seasonality.mode="multiplicative"表示时序季节趋势 的模式为乘法模式,如果该参数取值为additive,则表示为加法模式。
## 数据切分为训练集和测试集
train = df[0:120]
test = df[120:]
## 构建模型
model = Prophet(growth = "linear", # 线性增长趋势
yearly_seasonality = True, # 年周期的趋势
weekly_seasonality = False,# 以周为周期的趋势
daily_seasonality = False, # 以天为周期的趋势
seasonality_mode = "multiplicative", # 季节周期性模式
seasonality_prior_scale = 12, # 季节周期性长度
)
model.fit(train)
## 使用模型对测试集进行预测
forecast = model.predict(test)
## 输出部分预测结果
print(forecast[['ds', 'yhat', 'yhat_lower', 'yhat_upper']].head())
print("在测试集上绝对值预测误差为:",mean_absolute_error(test.y,forecast.yhat))运行结果如下:
INFO:numexpr.utils:NumExpr defaulting to 8 threads.
ds yhat yhat_lower yhat_upper
0 1959-01-01 368.542752 356.998558 379.747326
1 1959-02-01 358.317627 346.544210 370.858007
2 1959-03-01 406.314560 394.439755 418.404881
3 1959-04-01 395.163652 383.408878 406.728424
4 1959-05-01 404.083929 392.257283 416.820298
在测试集上绝对值预测误差为: 25.382391862162734从上面程序的输出结果中可以发现,模型在测试集上的绝对值预测误差为25.3556,是所有介绍过的模型中针对该数据预测效果最好的模型。
针对该模型的预测结果,可以使用下面的程序将其可视化,对比分析预测数据和原始数据之间的差异,程序运行后的结果如图6-21所示。
## 可视化原始数据和预测数据进行对比
fig, ax = plt.subplots()
train.plot(x = "ds",y = "y",figsize=(14,7),label="训练数据",ax = ax)
test.plot(x = "ds",y = "y",figsize=(14,7),label="测试数据",ax = ax)
forecast.plot(x = "ds",y = "yhat",style = "g--o",label="预测数据",ax = ax)
## 可视化出置信区间
ax.fill_between(test["ds"].values, forecast["yhat_lower"],
forecast["yhat_upper"],color='k',alpha=.2,
label = "95%置信区间")
plt.grid()
plt.xlabel("时间")
plt.ylabel("数值")
plt.title("Prophet模型")
plt.legend(loc=2)
plt.show()
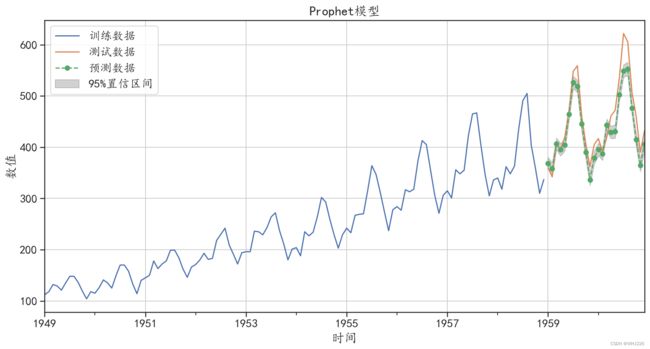
## 从可视化结果中可发现模型的预测效果很好运行结果如下:
图6-21 Prophet模型预测效果
从可视化结果中可以发现,模型的预测效果很好,把序列的增长趋势、周期趋势和小的波动都 预测出来了。
Prophet()函数获得的模型也可以使用 model.plot()方式可视化预测结果与真实值之间的差异, 运行下面的程序,结果如图6-22所示。
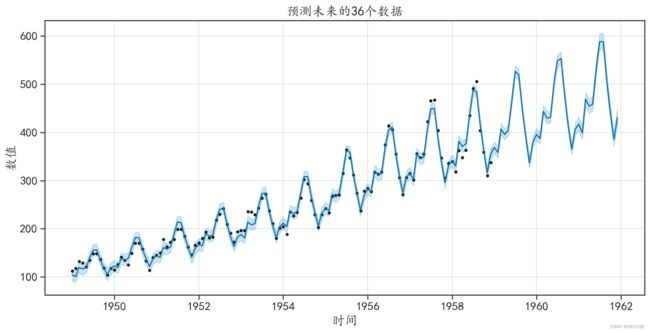
## 也可以通过model.make_future_dataframe获取对训练数据和未来数据进行预测的时间
future = model.make_future_dataframe(periods=36,freq = "MS")
forecast = model.predict(future)
## 可视化预测结果
model.plot(forecast,figsize=(12,6),xlabel = "时间",
ylabel = "数值")
plt.title("预测未来的36个数据")
plt.show()
## 在图像中散点是训练数据中的真实数据,曲线是模型的拟合数据和预测数据,
## 阴影则表示预测值的置信区间运行结果如下:
图6-22 预测结果可视化
图6-22中的散点是训练数据中的真实数据,曲线是模型的拟合数据和预测数据,阴影则表示 预测值的置信区间。
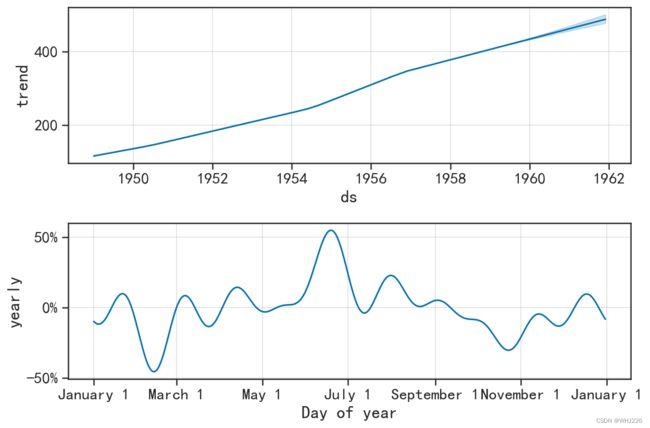
prophet 库中,还包含一个 prophet_plot_components()函数,该函数可以可视化模型的组成 部分,运行下面的程序,结果如图6-23所示。
## 使用model.plot_components可视化出模型中的主要成分
model.plot_components(forecast)
plt.show()
## 第一幅图表示模型中的线性变化趋势
## 第二幅图表示在一年的时间内数量的增长或见效快的变化情况运行结果如下:
图6-23 模型的主要部分可视化
图6-23(1)表示模型中的线性变化趋势,图(6-23(2))表示在一年的时间内乘客数量的 增加或减少的变化情况,即周期趋势。线性趋势表明乘客的数量是逐年增加的,周期趋势表明一年 中每个时间段数量的波动情况,发现3月份左右有一个最低点,7月份前后会出现高点。
经过前面3节对序列X1使用的多种预测算法的建模分析,下面将多种时序模型的预测效果和 误差进行总结,如表6-2所示。
6 多元时间序列ARIMAX模型
前面讨论的是一元时间序列,但在实际情况中,很多序列的变化规律会受到其他序列的影响, 往往需要建立多元时间序列ARIMAX 模型。ARIMAX 模型是指带回归项的ARIMA 模型,又称扩 展的ARIMA模型,回归项的引入有利于提高模型的预测效果。引入的回归项一般是与预测对象(即 被解释变量)相关程度较高的变量。比如,分析居民的消费支出序列时,消费会受到收入的影响, 如果将收入也纳入研究范围,就能得到更精确的消费预测。
本节将以一个简单的二维时间序列为例,介绍如何使用Python完成ARIMAX模型的建立和使
用。
6.1 数据准备与可视化
在建立ARIMAX 模型时,本节会使用燃气炉数据集(gas furnace data.xlsx),该数据中包 含天然气的输入速率和CO2的输出浓度随时间变化的情况,读取数据的程序如下:
## 读取数据
datadf = pd.read_csv("E:/PYTHON/gas furnace data.txt",sep="\s+")
datadf.columns = ["GasRate","C02"]
## GasRate:输入天然气速率,C02:输出二氧化碳浓度
print(datadf.head())运行结果如下:
GasRate C02
0 -0.109 53.8
1 0.000 53.6
2 0.178 53.5
3 0.339 53.5
4 0.373 53.4读取的数据中 GasRate表示输入的天然气速率, CO2表示输出的二氧化碳浓度。针对数据中 两个变量的波动情况,可使用下面的程序进行可视化,程序运行后的结果如图6-24所示。
## 可视化出两个序列的变换情况
plt.figure(figsize=(14,6))
plt.subplot(1,2,1)
datadf.GasRate.plot(c="r")
plt.grid()
plt.xlabel("Observation")
plt.ylabel("Gas Rate")
plt.subplot(1,2,2)
datadf.C02.plot(c="r")
plt.grid()
plt.xlabel("Observation")
plt.ylabel("C02")
plt.show()运行结果如下:
图6-24 两个序列的波动情况
对数据建立ARIMAX模型之前,先将数据切分为训练集和测试集,将前面75%的样本作为训 练集,将剩下的作为测试集,程序如下,从输出结果中可见,训练集包含222个样本组,测试集包 含74个样本组。
## 前面百分之75做训练集,后面百分之25做测试集
trainnum = np.int(datadf.shape[0]*0.75)
traidata = datadf.iloc[0:trainnum,:]
testdata = datadf.iloc[trainnum:datadf.shape[0],:]
print(traidata.shape)
print(testdata.shape)运行结果如下:
(222, 2)
(74, 2)建模之前可以使用单位根检验,分析两个序列是否为平稳序列,程序如下,从输出结果中可以 发现,两个序列的p-value均小于0.05,说明在置信度为95%的水平下,两序列均为平稳序列, 可以利用ARIMAX模型进行预测。
## 1:单位根检验检验序列的平稳性,ADF 检验
dftest = adfuller(datadf.GasRate,autolag='BIC')
dfoutput = pd.Series(dftest[0:4],
index=['adf','p-value','usedlag','Number of Observations Used'])
print("GasRate 检验结果:\n",dfoutput)
dftest = adfuller(datadf.C02,autolag='BIC')
dfoutput = pd.Series(dftest[0:4],
index=['adf','p-value','usedlag','Number of Observations Used'])
print("C02 检验结果:\n",dfoutput)
## p-value均小于0.05,说明在置信度为95%水平下,两个序列均是平稳序列。运行结果如下:
GasRate 检验结果:
adf -4.878952
p-value 0.000038
usedlag 2.000000
Number of Observations Used 293.000000
dtype: float64
C02 检验结果:
adf -2.947057
p-value 0.040143
usedlag 3.000000
Number of Observations Used 292.000000
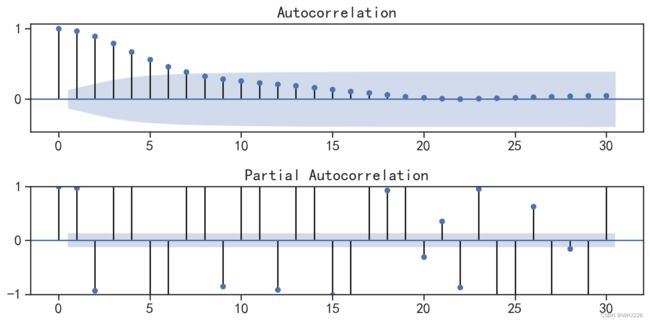
dtype: float64针对待预测序列的因变量,可以使用自相关图和偏自相关图对序列进行分析,运行下面的程序, 结果如图6-25所示。
## 可视化序列的自相关和偏相关图
fig = plt.figure(figsize=(10,5))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(traidata.C02, lags=30, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(traidata.C02, lags=30, ax=ax2)
plt.ylim([-1,1])
plt.tight_layout()
plt.show()运行结果如下:
图6-25 CO2序列的自相关图和偏自相关图
6.2 ARIMAX模型建立与预测
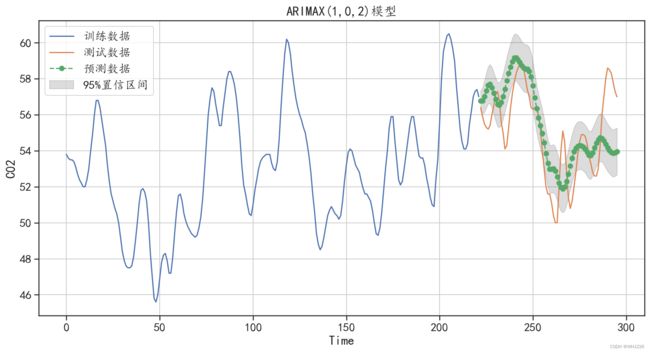
通过前面的分析,首先使用 pf.ARIMAX()函数对数据建立ARIMAX(1,0,2)模型,程序如下:
## 建立ARIMAX(1,0,2)模型
model = pf.ARIMAX(data=traidata,formula="C02~GasRate",ar=1,ma=2,integ=0)
model_1 = model.fit("MLE")
model_1.summary()运行结果如下:
Normal ARIMAX(1,0,2)
======================================================= ==================================================
Dependent Variable: C02 Method: MLE
Start Date: 2 Log Likelihood: -71.9362
End Date: 221 AIC: 155.8725
Number of observations: 220 BIC: 176.2343
==========================================================================================================
Latent Variable Estimate Std Error z P>|z| 95% C.I.
======================================== ========== ========== ======== ======== =========================
AR(1) 0.9086 0.0191 47.5425 0.0 (0.8712 | 0.9461)
MA(1) 1.0231 0.0552 18.5272 0.0 (0.9149 | 1.1314)
MA(2) 0.6231 0.0442 14.1127 0.0 (0.5365 | 0.7096)
Beta 1 4.8793 1.0166 4.7996 0.0 (2.8868 | 6.8719)
Beta GasRate -0.4057 0.0533 -7.613 0.0 (-0.5102 | -0.3013)
Normal Scale 0.3356
==========================================================================================================从上面的输出结果中可以发现模型的AIC=155.8725,并且每个系数的显著性检验结果表明自 已是显著的。针对拟合的模型可以使用 plot_fit()方法可视化数据在训练集上的拟合情况,运行下面 的程序后,拟合结果如图6-26所示。
## 可视化模型在训练集上的拟合情况
model.plot_fit(figsize=(10,5))运行结果如下:
图6-26 在训练集上的拟合结果
从图6-26中可以发现,在训练集上的拟合效果很好。通过拟合模型的plot_predict()方法,可 以可视化模型在测试集上的预测效果,运行下面的程序后,结果如图6-27所示。
## 可视化模型的在测试集上的预测结果
model.plot_predict(h=testdata.shape[0], ## 往后预测的数目
oos_data=testdata, ## 测试数据集
past_values=traidata.shape[0], ## 图像显示训练集的多少数据
figsize=(14,7))
plt.show()运行结果如下:
图6-27 对测试集的预测结果
在图6-27中并没有同时可视化出测试集与测试集的预测值,因此使用下面的程序对预测结果 进行可视化对比,程序运行后的结果如图6-28所示。
## 预测新的数据
C02pre = model.predict(h=testdata.shape[0], ## 往后预测多少步
oos_data=testdata, ## 测试数据集
intervals=True, ## 同时预测置信区间
)
print("在测试集上绝对值预测误差为:",mean_absolute_error(testdata.C02,C02pre.C02))
print(C02pre.head())运行结果如下:
在测试集上绝对值预测误差为: 1.5731456243696424
C02 1% Prediction Interval 5% Prediction Interval \
222 56.770585 55.988034 56.225457
223 56.772237 55.720472 56.039130
224 57.009510 55.771620 56.138492
225 57.339511 55.978476 56.376392
226 57.635704 56.191302 56.611199
95% Prediction Interval 99% Prediction Interval
222 57.331513 57.563458
223 57.504168 57.818328
224 57.877225 58.232795
225 58.300240 58.702436
226 58.661854 59.081403 ## 可视化原始数据和预测数据进行对比
traidata.C02.plot(figsize=(14,7),label="训练数据")
testdata.C02.plot(figsize=(14,7),label="测试数据")
C02pre.C02.plot(style = "g--o",label="预测数据")
## 可视化出置信区间
plt.fill_between(C02pre.index, C02pre["5% Prediction Interval"],
C02pre["95% Prediction Interval"],color='k',alpha=.15,
label = "95%置信区间")
plt.grid()
plt.xlabel("Time")
plt.ylabel("C02")
plt.title("ARIMAX(1,0,2)模型")
plt.legend(loc=2)
plt.show()运行结果如下:
图6-28 ARIMAX 模型对测试集的预测结果
从输出的结果中可以发现,预测值在开始部分很好地拟合了真实数据的变化趋势,但是后面的 预测结果就变得不准确了。这说明时间序列预测的相关算法在短期内还是非常有效的,所以在实际 应用中,尽可能在短期预测中应用。
针对ARIMAX 模型,可以使用循环建模的方式,对参数p和q进行搜索,获得拟合效果更好 的模型,可以使用下面的程序计算每种p和q的组合下拟合模型的BIC值和在测试集上的预测绝对 值误差。
## 参数搜索寻找合适的p,q
p = np.arange(6)
q = np.arange(6)
pp,qq = np.meshgrid(p,q)
resultdf = pd.DataFrame(data = {"arp":pp.flatten(),"mrq":qq.flatten()})
resultdf["bic"] = np.double(pp.flatten())
resultdf["mae"] = np.double(qq.flatten())
## 迭代循环建立多个模型
for ii in resultdf.index:
model_i = pf.ARIMAX(data=traidata,formula="C02~GasRate",ar=resultdf.arp[ii],ma=resultdf.mrq[ii],integ=0)
try:
modeli_fit = model_i.fit("MLE")
bic = modeli_fit.bic
C02_pre = model.predict(h=testdata.shape[0],oos_data=testdata)
mae = mean_absolute_error(testdata.C02,C02_pre.C02)
except:
bic = np.nan
resultdf.bic[ii] = bic
resultdf.mae[ii] = mae
print("模型迭代结束")在模型选代结束后,可以根据BIC取值的大小进行排序,输出预测效果较好的模型,运行下面 的程序可以发现,在参数p=3、g=2时,获得的模型效果较好,在测试集上的绝对值误差较小。
## 按照BIC寻找合适的模型
print(resultdf.sort_values(by="bic").head())运行结果如下:
arp mrq bic mae
15 3 2 0.820429 1.573146
17 5 2 21.192451 1.573146
11 5 1 29.406913 1.573146
28 4 4 31.267202 1.573146
27 3 4 44.280754 1.573146使用获得的最好参数可以重新利用数据拟合新的ARIMAX(3,2)模型,程序如下,程序中还对测 试集进行了预测,并将预测的结果进行可视化,还和原始的测试值进行对比分析,程序运行后的结 果如图6-29所示。
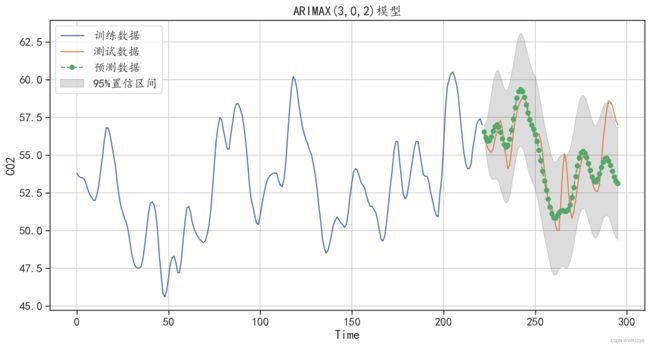
## 重新建立效果较好的模型
model = pf.ARIMAX(data=traidata,formula="C02~GasRate",ar=3,ma=2,integ=0)
model_1 = model.fit("MLE")
model_1.summary()运行结果如下:
Normal ARIMAX(3,0,2)
======================================================= ==================================================
Dependent Variable: C02 Method: MLE
Start Date: 3 Log Likelihood: 20.4678
End Date: 221 AIC: -24.9356
Number of observations: 219 BIC: 2.177
==========================================================================================================
Latent Variable Estimate Std Error z P>|z| 95% C.I.
======================================== ========== ========== ======== ======== =========================
AR(1) 2.3482 0.0372 63.075 0.0 (2.2753 | 2.4212)
AR(2) -1.9578 0.0658 -29.7577 0.0 (-2.0867 | -1.8288)
AR(3) 0.5787 0.0306 18.8919 0.0 (0.5187 | 0.6387)
MA(1) -0.928 0.0745 -12.456 0.0 (-1.074 | -0.782)
MA(2) 0.0028 0.0738 0.0383 0.9695 (-0.1418 | 0.1474)
Beta 1 1.642 0.1027 15.9821 0.0 (1.4406 | 1.8433)
Beta GasRate -0.1093 0.0067 -16.2376 0.0 (-0.1225 | -0.0961)
Normal Scale 0.2223
==========================================================================================================## 预测新的数据
C02pre = model.predict(h=testdata.shape[0], ## 往后预测多少步
oos_data=testdata, ## 测试数据集
intervals=True)
print("在测试集上绝对值预测误差为:",mean_absolute_error(testdata.C02,C02pre.C02))
## 可视化原始数据和预测数据进行对比
traidata.C02.plot(figsize=(14,7),label="训练数据")
testdata.C02.plot(figsize=(14,7),label="测试数据")
C02pre.C02.plot(style = "g--o",label="预测数据")
## 可视化出置信区间
plt.fill_between(C02pre.index, C02pre["5% Prediction Interval"],
C02pre["95% Prediction Interval"],color='k',alpha=.15,
label = "95%置信区间")
plt.grid()
plt.xlabel("Time")
plt.ylabel("C02")
plt.title("ARIMAX(3,0,2)模型")
plt.legend(loc=2)
plt.show()运行结果如下:
在测试集上绝对值预测误差为: 1.1115309949695789图6-29 ARIMAX(3,2)模型的预测结果
可以发现,使用ARIMAX(3,2)模型对测试集的预测误差更小,对测试集的预测效果更好。
7 时序数据的异常值检测
分析时间序列的波动情况时,可以将突然增大或者突然减小的数据无规律看作异常值。判断一个数据是否为异常值,可以使用Facebook发布的Prophet模型进行检测。最直接的方式是将数据 波动情况拟合值的置信区间,作为判断是否为异常值的上下界。下面使用一个时间序列数据,检测 其是否存在异常值。
7.1 数据准备与可视化
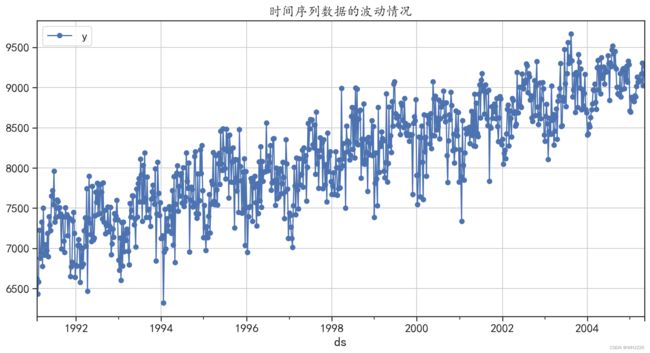
使用的时间序列数据(简称时序数据)为从1991年2月到2005年5月,每周提供美国成品 汽车汽油产品的时间序列(每天数干桶)。使用下面的程序可以对数据进行读取并可视化,结果如 图6-30所示。
## 使用prophet检测时间序列是否有异常值
## 从1991年2月到2005年5月,每周提供美国成品汽车汽油产品的时间序列(每天数千桶)
## 数据准备
data = pm.datasets.load_gasoline()
datadf = pd.DataFrame({"y":data})
datadf["ds"] = pd.date_range(start="1991-2",periods=len(data),freq="W")
## 可视化时间序列的变化情况
datadf.plot(x = "ds",y = "y",style = "b-o",figsize=(14,7))
plt.grid()
plt.title("时间序列数据的波动情况")
plt.show()运行结果如下:
图6-30 时间序列数据的波动情况
7.2 时序数据异常值检测
针对前面的时序数据,可以使用下面的程序建立时序数据拟合模型,对数据变化趋势和波动情 况进行拟合,并且在模型的预测结果中包含预测值的上界和下界(默认为置信度95%的上下界)。
## 对该数据建立一个时间序列模型
np.random.seed(1234) ## 设置随机数种子
model = Prophet(growth="linear",daily_seasonality = False,
weekly_seasonality=False,
seasonality_mode = 'multiplicative',
interval_width = 0.95, ## 获取95%的置信区间
)
model = model.fit(datadf) # 使用数据拟合模型
forecast = model.predict(datadf) # 使用模型对数据进行预测
forecast["y"] = datadf["y"].reset_index(drop = True)
forecast[["ds","y","yhat","yhat_lower","yhat_upper"]].head()运行结果如下:
ds y yhat yhat_lower yhat_upper
0 1991-02-03 6621.0 6767.051491 6294.125979 7303.352309
1 1991-02-10 6433.0 6794.736479 6299.430616 7305.414252
2 1991-02-17 6582.0 6855.096282 6352.579489 7379.717614
3 1991-02-24 7224.0 6936.976642 6415.157617 7445.523000
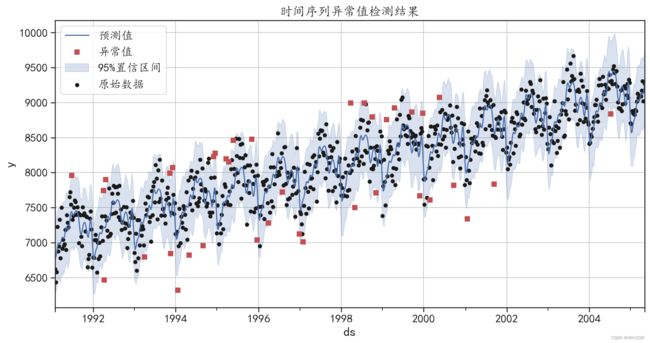
4 1991-03-03 6875.0 6990.511503 6489.781400 7488.240435下面定义一个函数 outlier_detection(),该函数会使用模型预测值的置信区间的上下界,来判 断样本是否为异常值。判断序列是否为异常值的程序如下,从输出结果中可以发现,序列中一共发 现了38个异常值。
## 根据模型预测值的置信区间"yhat_lower"和"yhat_upper"判断样本是否为异常值
def outlier_detection(forecast):
index = np.where((forecast["y"] <= forecast["yhat_lower"])|
(forecast["y"] >= forecast["yhat_upper"]),True,False)
return index
outlier_index = outlier_detection(forecast)
outlier_df = datadf[outlier_index]
print("异常值的数量为:",np.sum(outlier_index))运行结果如下:
异常值的数量为: 38使用下面的程序可以将异常值的位置等数据信息可视化,程序运行后的结果如图6-31所示。
## 可视化异常值的结果
fig, ax = plt.subplots()
## 可视化预测值
forecast.plot(x = "ds",y = "yhat",style = "b-",figsize=(14,7),
label = "预测值",ax=ax)
## 可视化出置信区间
ax.fill_between(forecast["ds"].values, forecast["yhat_lower"],
forecast["yhat_upper"],color='b',alpha=.2,
label = "95%置信区间")
forecast.plot(kind = "scatter",x = "ds",y = "y",c = "k",
s = 20,label = "原始数据",ax = ax)
## 可视化出异常值的点
outlier_df.plot(x = "ds",y = "y",style = "rs",ax = ax,
label = "异常值")
plt.legend(loc = 2)
plt.grid()
plt.title("时间序列异常值检测结果")
plt.show()运行结果如下:
图6-31 时间序列异常值检验结果
从图6-31中可以发现,异常值大部分在置信区间之外,有些异常值是因为取值较大,有部分 异常值是因为取值较小。
笔记摘自——《Python机器学习算法与实战》