决策树(ID3,C4.5,CART,基于 sklearn 和 Numpy 实现)
本文中使用的数据集以及源码machine-learning/decision-tree at Stellaris.github.io · Stellaris123/machine-learning
决策树是基于特征对数据实例按照条件不断的划分,最终达成分类或回归的目的。决策树模型预测的过程可以看作是多个 if-then 条件的集合,也可以视作定义在特征空间于类空间中的条件概率分布。
决策树的核心包括:①特征选择,②决策树构建,③决策树剪枝。
从条件概率分布的角度理解决策树模型:
假设将特征空间划分为互不相交的区域,每个区域定义的类的概率分布就构成了一个条件概率分布。决策树所表示的条件概率分布是由各个区域给定类的条件概率分布组成的。假设 X X X 为特征的随机变量, Y Y Y 为类的随机变量,相应的条件概率分布可以表示为 P ( Y ∣ X ) P(Y|X) P(Y∣X)。当叶子节点上的条件概率分布偏向每一类时,那么属于该类的概率就比较大。从这个角度看,决策树也是一种概率模型。
基本思想
(1)使用属性选择度量 ( A S M ) (ASM) (ASM) 选择最佳属性来分割数据。
(2)将该属性作为决策节点,并将数据集分解为更小的子集。
(3)通过对每个子节点递归地重复这个过程,直到下列其中一个条件满足:
①所有样本数据都属于同一个类别。
②没有剩余的属性。
③没有剩余的样本数据。
引入问题
| 天气 | 温度 | 湿度 | 是否有风 | 是否打高尔夫 |
|---|---|---|---|---|
| 晴 | 热 | 高 | 否 | 否 |
| 晴 | 热 | 高 | 是 | 否 |
| 阴 | 热 | 高 | 否 | 是 |
| 雨 | 适宜 | 高 | 否 | 是 |
| 雨 | 冷 | 正常 | 否 | 是 |
| 雨 | 冷 | 正常 | 是 | 否 |
| 阴 | 冷 | 正常 | 是 | 是 |
| 晴 | 适宜 | 高 | 否 | 否 |
| 晴 | 冷 | 正常 | 否 | 是 |
| 雨 | 适宜 | 正常 | 否 | 是 |
| 晴 | 适宜 | 正常 | 是 | 是 |
| 阴 | 适宜 | 高 | 是 | 是 |
| 阴 | 热 | 正常 | 否 | 是 |
| 雨 | 适宜 | 高 | 是 | 否 |
特征选择
特征选择 & 属性选择度量
决策树的每一次分支都要选取一个特征,如果一个特征能够使得分类后的分支节点尽可能属于同一类别(纯度高),那么就说这个特征有对数据集有较强的分类能力,决策树的特征选择就是从数据集中选择具备较强分类能力的特征类对数据集进行划分。
属性选择度量是一种启发式的选择分割准则,将数据划分为尽可能最佳的方式。它也被称为分割规则,因为它帮助我们确定给定节点上的分割点。ASM通过解释给定的数据集为每个特征(或属性)提供一个排名。最佳得分属性将被选择为分割属性(源)。在连续值属性的情况下,还需要定义分支的分割点。
常见的决策树特征选择方法:信息增益、信息增益比和基尼指数,对应三种决策树算法: I D 3 ID3 ID3, C 4.5 C4.5 C4.5, C A R T CART CART。
信息增益
熵和条件熵
熵是一种描述随机变量不确定性(样本集合纯度)的度量方式。熵越低,样本的不确定性越小,纯度越高。
假设当前样本数据集 D D D 中第 i i i 个类所占比例(概率)为 p i ( i = 1 , 2 , … , k ) p_i(i=1,2,\dots,k) pi(i=1,2,…,k),那么该样本数据集的熵可定义为:
E ( D ) = − ∑ i = 1 k p i l o g p i (1) E(D)=-\sum_{i=1}^{k}p_ilog^{p_i} \tag{1} E(D)=−i=1∑kpilogpi(1)
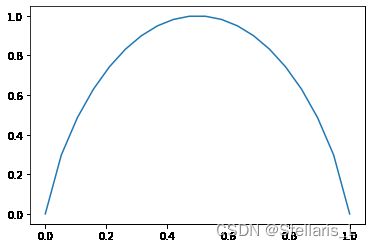
p0 = np.linspace(0, 1, 20)
p1 = 1 - p0
entropy = -p0 * np.log2(p0 + 1e-9) - p1 * np.log2(p1 + 1e-9)
plt.plot(p0, entropy)
从上图中可以发现,对于只有两个类别的数据,当两个类别数据各占一半时,熵最大,而只有一种类别时,熵为0。所以当熵越小,分类的纯度越高。
假设离散随机变量 ( X , Y ) (X,Y) (X,Y) 的联合概率分布为:
P ( X = x i , Y = y j ) = p i j (2) P(X=x_i,Y=y_j)=p_{ij} \tag{2} P(X=xi,Y=yj)=pij(2)
条件熵 E ( Y ∣ X ) E(Y|X) E(Y∣X) 表示在已知随机变量 X X X 的前提下 Y Y Y 的不确定性的度量, E ( Y ∣ X ) E(Y|X) E(Y∣X) 可定义为在给定 X X X 的条件下 Y Y Y 的条件概率分布的熵对 X X X 的数学期望。可表示为:
E ( Y ∣ X ) = ∑ i = 1 k P ( X = x i ) E ( Y ∣ X = x i ) (3) \\ E(Y|X)=\sum_{i=1}^{k}P(X=x_i)E(Y|X=x_i) \tag{3} E(Y∣X)=i=1∑kP(X=xi)E(Y∣X=xi)(3)
在实际计算时,熵和条件熵中的概率计算是基于极大似然估计得到的,对应的熵和条件熵也被称为经验熵和经验条件熵。
信息增益
信息增益定义为:由于得到特征 X X X 的信息而使得类 Y Y Y 的信息不确定性减少的程度,即信息增益是一种描述目标类别确定性增加的量,特征的信息增益越大,代表对应的特征分类能力越强。选择信息增益最大的特征作为决策树划分节点。
假设训练集 D D D 的经验熵为 E ( D ) E(D) E(D),特征 A A A 的条件下 D D D 的经验条件熵为 E ( D ∣ A ) E(D|A) E(D∣A),那么信息增益可定义为:
g ( D , A ) = E ( D ) − E ( D ∣ A ) (4) g(D,A)=E(D)-E(D|A) \tag{4} g(D,A)=E(D)−E(D∣A)(4)
样例计算:
以上表高尔夫数据集为例,计算天气特征对于数据集的信息增益。
(1)计算该数据集的经验熵 E ( D ) E(D) E(D)。
经验熵 E ( D ) E(D) E(D) 依赖于目标变量,即是否打高尔夫的概率分布。
| 是 | 否 |
|---|---|
| 9 | 5 |
E ( 是 否 打 高 尔 夫 ) = E ( 5 , 9 ) = E ( 0.36 , 0.64 ) = − 0.36 × l o g 2 ( 0.36 ) − 0.64 × l o g 2 ( 0.64 ) ≈ 0.94 (5) \begin{aligned} E(是否打高尔夫)& =E(5,9)=E(0.36,0.64) \\& =-0.36\times log_2(0.36)-0.64\times log_2(0.64)\approx0.94 \end{aligned} \tag{5} E(是否打高尔夫)=E(5,9)=E(0.36,0.64)=−0.36×log2(0.36)−0.64×log2(0.64)≈0.94(5)
(2)计算天气特征的经验条件熵 E ( D ∣ A ) E(D|A) E(D∣A)。
在不同天气条件条件下是否打高尔夫进行统计。
| 特征 | 种类 | 是 | 否 | 总 |
|---|---|---|---|---|
| 晴 | 2 | 3 | 5 | |
| 天气 | 阴 | 4 | 0 | 4 |
| 雨 | 3 | 2 | 5 | |
| 14 |
E ( 是 否 打 高 尔 夫 ∣ 天 气 ) = p ( 晴 ) × E ( 2 , 3 ) + p ( 阴 ) × E ( 4 , 0 ) + p ( 雨 ) × E ( 3 , 2 ) = ( 5 14 ) × 0.97 + ( 4 14 ) × 0 + ( 5 14 ) × 0.97 ≈ 0.69 (6) \begin{aligned} E(是否打高尔夫|天气)& =p(晴)\times E(2,3)+p(阴)\times E(4,0)+p(雨)\times E(3,2) \\& =(\frac{5}{14})\times 0.97+(\frac{4}{14})\times 0+(\frac{5}{14})\times 0.97\approx 0.69 \end{aligned} \tag{6} E(是否打高尔夫∣天气)=p(晴)×E(2,3)+p(阴)×E(4,0)+p(雨)×E(3,2)=(145)×0.97+(144)×0+(145)×0.97≈0.69(6)
(3)计算天气特征的信息增益 g ( D , A ) g(D,A) g(D,A)。
将经验熵和经验条件熵做差,即可得到天气特征的信息增益。
g ( 是 否 打 高 尔 夫 , 天 气 ) = E ( 是 否 打 高 尔 夫 ) − E ( 是 否 打 高 尔 夫 ∣ 天 气 ) = 0.94 − 0.69 = 0.25 (7) \begin{aligned} g(是否打高尔夫,天气)& =E(是否打高尔夫)-E(是否打高尔夫|天气) \\& =0.94-0.69=0.25 \end{aligned} \tag{7} g(是否打高尔夫,天气)=E(是否打高尔夫)−E(是否打高尔夫∣天气)=0.94−0.69=0.25(7)
最后计算出天气的信息增益约为 0.25 0.25 0.25。
使用 Numpy 计算
(1)定义熵计算
import numpy as np
from math import log
def entropy(ele):
"""
输入:
->ele:包含类别取值的列表
输出:
->entropy:信息熵值
"""
# 计算列表中取值的概率分布
probs = [ele.count(i)/len(ele) for i in set(ele)]
# 计算信息熵
entropy = -sum(prob*log(prob,2) for prob in probs)
return entropy
(2)信息增益计算
import pandas as pd
# 以数据集框架读取高尔夫数据集
df = pd.read_csv("./golf_data.csv")
# 计算数据集的经验熵
# "play"为目标变量,即是否打高尔夫
entropy_D = entropy(df["play"].tolist())
# 计算天气特征的经验条件熵
# 其中 subset1,subset2,subset3 为根据天气特征三个取值划分之后的子集
subset1 = df[df["outlook"]=="sunny"]
subset2 = df[df["outlook"]=="overcast"]
subset3 = df[df["outlook"]=="rainy"]
entropy_DA = len(subset1)/len(df)*entropy(subset1["play"].tolist()) + \
len(subset2)/len(df)*entropy(subset2["play"].tolist()) + \
len(subset3)/len(df)*entropy(subset3["play"].tolist())
# 计算天气特征的信息增益
info_gain = entropy_D - entropy_DA
print(info_gain)
print:0.2467498197744391
信息增益存在的问题
当某个特征分类取值较多的时,该特征的信息增益计算结果就会较大。 可能存在一个特征,每个数据的类别都不同,这样该特征就会产生很多的分支,其中每个分支的纯度都很高,最后的信息增益也很高,但是这样的分类在实际情况上是无法使用的。所以,基于信息增益选择特征时,会偏向取值较大的特征。这就是信息增益比。
信息增益比
使用信息增益比可以对信息增益存在的问题进行校正。特征 A A A 对数据集 D D D 的信息增益比可以定义为其信息增益 g ( D , A ) g(D,A) g(D,A) 与数据集 D D D 关于特征 A A A 取值的熵 E A ( D ) E_A(D) EA(D) 的比值,信息增益比越大的特征作为划分效果越好。(n 表示某一特征 A A A 的取值个数)
g R ( D , A ) = g ( D , A ) E A ( D ) E A ( D ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ l o g 2 ∣ D i ∣ ∣ D ∣ (8) g_R(D,A)=\frac{g(D,A)}{E_A(D)} \\ E_A(D)=-\sum_{i=1}^{n}\frac{|D_i|}{|D|}log_2^{\frac{|D_i|}{|D|}} \tag{8} gR(D,A)=EA(D)g(D,A)EA(D)=−i=1∑n∣D∣∣Di∣log2∣D∣∣Di∣(8)
具体计算
以上表高尔夫数据集为例,计算天气特征对于数据集的信息增益比。
(1)计算天气特征信息增益 g ( D , A ) g(D,A) g(D,A)。
根据式 ( 7 ) (7) (7),天气特征的信息增益 g ( 是 否 打 高 尔 夫 , 天 气 ) ≈ 0.25 g(是否打高尔夫,天气)\approx0.25 g(是否打高尔夫,天气)≈0.25。
(2)计算高尔夫数据集关于天气特征取值的熵 E A ( D ) E_A(D) EA(D)。
| 特征 | 种类 | 是 | 否 | 总 |
|---|---|---|---|---|
| 晴 | 2 | 3 | 5 | |
| 天气 | 阴 | 4 | 0 | 4 |
| 雨 | 3 | 2 | 5 | |
| 14 |
E 天 气 ( 是 否 打 高 尔 夫 ) = − ( ( 5 14 ) × l o g 2 ( 5 14 ) + ( 4 14 ) × l o g 2 ( 4 14 ) + ( 5 14 ) × l o g 2 ( 5 14 ) ) ≈ 1.58 (9) \begin{aligned} E_{天气}(是否打高尔夫)& =-((\frac{5}{14})\times log_2(\frac{5}{14})+(\frac{4}{14})\times log_2(\frac{4}{14})+(\frac{5}{14})\times log_2(\frac{5}{14})) \\& \approx 1.58 \end{aligned} \tag{9} E天气(是否打高尔夫)=−((145)×log2(145)+(144)×log2(144)+(145)×log2(145))≈1.58(9)
(3)计算天气特征的信息增益比 g R ( D , A ) g_R(D,A) gR(D,A)。
g R ( 是 否 打 高 尔 夫 , 天 气 ) = g ( 是 否 打 高 尔 夫 , 天 气 ) E 天 气 ( 是 否 打 高 尔 夫 ) = 0.25 1.58 ≈ 0.16 (10) g_R(是否打高尔夫,天气)=\frac{g(是否打高尔夫,天气)}{E_{天气}(是否打高尔夫)}=\frac{0.25}{1.58}\approx 0.16 \tag{10} gR(是否打高尔夫,天气)=E天气(是否打高尔夫)g(是否打高尔夫,天气)=1.580.25≈0.16(10)
Numpy计算
(1)定义熵计算
import numpy as np
from math import log
def entropy(ele):
"""
输入:
->ele:包含类别取值的列表
输出:
->entropy:信息熵值
"""
# 计算列表中取值的概率分布
probs = [ele.count(i)/len(ele) for i in set(ele)]
# 计算信息熵
entropy = -sum(prob*log(prob,2) for prob in probs)
return entropy
(2)信息增益比计算
import pandas as pd
# 以数据集框架读取高尔夫数据集
df = pd.read_csv("./golf_data.csv")
# 计算数据集的经验熵
# "play"为目标变量,即是否打高尔夫
entropy_D = entropy(df["play"].tolist())
# 计算天气特征的经验条件熵
# 其中 subset1,subset2,subset3 为根据天气特征三个取值划分之后的子集
subset1 = df[df["outlook"]=="sunny"]
subset2 = df[df["outlook"]=="overcast"]
subset3 = df[df["outlook"]=="rainy"]
entropy_DA = len(subset1)/len(df)*entropy(subset1["play"].tolist()) + \
len(subset2)/len(df)*entropy(subset2["play"].tolist()) + \
len(subset3)/len(df)*entropy(subset3["play"].tolist())
# 计算天气特征的信息增益
info_gain = entropy_D - entropy_DA
# 计算天气特征的信息增益比
entropy_A = entropy(df["outlook"].tolist())
info_gain_rate = info_gain/entropy_A
print(info_gain)
print(info_gain_rate)
基尼指数
基尼指数是针对概率分布而言的(关于基尼指数和基尼系数的区别可以看尾注)。假设样本有 k k k 个类,样本属于第 i i i 类的概率为 p i p_i pi,则该样本类别概率分布的基尼指数可定义为:
g i n i ( p ) = ∑ i = 1 k p i ( 1 − p i ) = 1 − ∑ i = 1 k p i 2 (11) gini(p)=\sum_{i=1}^{k}p_i(1-p_i)=1-\sum_{i=1}^{k}p_i^2 \tag{11} gini(p)=i=1∑kpi(1−pi)=1−i=1∑kpi2(11)
对于给定训练集 D D D, C i C_i Ci 是属于第 i i i 类样本的集合,则该训练集的基尼指数可定义为:
g i n i ( D ) = 1 − ∑ i = 1 k ( ∣ C i ∣ ∣ D ∣ ) 2 (12) gini(D)=1-\sum_{i=1}^{k}(\frac{|C_i|}{|D|})^2 \tag{12} gini(D)=1−i=1∑k(∣D∣∣Ci∣)2(12)
如果训练集 D D D 根据特征 A A A 某一取值 a a a 划分为 D 1 , D 2 D_1,D_2 D1,D2 两个部分,那么在特征 A A A 的条件下,训练集 D D D 的基尼指数可以表示为:
g i n i ( D , A ) = D 1 D g i n i ( D 1 ) + D 2 D g i n i ( D 2 ) (13) gini(D,A)=\frac{D_1}{D}gini(D_1)+\frac{D_2}{D}gini(D_2) \tag{13} gini(D,A)=DD1gini(D1)+DD2gini(D2)(13)
训练集 D D D 的基尼指数 g i n i ( D ) gini(D) gini(D) 表示该集合的不确定性, g i n i ( D , A ) gini(D,A) gini(D,A) 表示训练集 D D D 经过 A = a A=a A=a 划分后的不确定性。基尼指数越小,对应的特征对训练样本的分类能力越强。
具体计算
以上表高尔夫数据集为例,计算天气特征对于数据集的基尼指数。
(1)求天气特征的基尼指数 G i n i ( D , A ) Gini(D,A) Gini(D,A)。
| 特征 | 种类 | 是 | 否 | 总 |
|---|---|---|---|---|
| 晴 | 2 | 3 | 5 | |
| 天气 | 阴 | 4 | 0 | 4 |
| 雨 | 3 | 2 | 5 | |
| 14 |
G i n i ( D , 天 气 = 晴 ) = 5 14 ( 2 × 2 5 × ( 1 − 2 5 ) + 9 14 ( 2 × 2 9 × ( 1 − 2 9 ) ) ) ≈ 0.39 G i n i ( D , 天 气 = 阴 ) ≈ 0.36 G i n i ( D , 天 气 = 雨 ) ≈ 0.46 (14) \begin{aligned} & Gini(D,天气=晴)=\frac{5}{14}(2\times \frac{2}{5}\times(1-\frac{2}{5})+\frac{9}{14}(2\times \frac{2}{9}\times(1-\frac{2}{9})))\approx 0.39 \\ & Gini(D,天气=阴)\approx 0.36 \\ & Gini(D,天气=雨)\approx 0.46 \end{aligned} \tag{14} Gini(D,天气=晴)=145(2×52×(1−52)+149(2×92×(1−92)))≈0.39Gini(D,天气=阴)≈0.36Gini(D,天气=雨)≈0.46(14)
可以看出 G i n i ( D , 天 气 = 阴 ) Gini(D,天气=阴) Gini(D,天气=阴) 最小,所以天气取值为阴可以选做天气特征的最优划分点。
(2)计算最优特征
高尔夫数据集一共有四种特征:
| 天气 | 温度 | 湿度 | 是否有风 |
|---|---|---|---|
| G i n i ( D , 天 气 = 晴 ) ≈ 0.39 Gini(D,天气=晴)\approx 0.39 Gini(D,天气=晴)≈0.39 | G i n i ( D , 温 度 = 热 ) ≈ 0.29 Gini(D,温度=热)\approx 0.29 Gini(D,温度=热)≈0.29 | G i n i ( D , 湿 度 = 高 ) ≈ 0.37 Gini(D,湿度=高)\approx 0.37 Gini(D,湿度=高)≈0.37 | G i n i ( D , 是 否 有 风 = 是 ) ≈ 0.43 Gini(D,是否有风=是)\approx 0.43 Gini(D,是否有风=是)≈0.43 |
| G i n i ( D , 天 气 = 阴 ) ≈ 0.36 Gini(D,天气=阴)\approx 0.36 Gini(D,天气=阴)≈0.36 | G i n i ( D , 温 度 = 适 宜 ) ≈ 0.23 Gini(D,温度=适宜)\approx 0.23 Gini(D,温度=适宜)≈0.23 | ||
| G i n i ( D , 天 气 = 雨 ) ≈ 0.46 Gini(D,天气=雨)\approx 0.46 Gini(D,天气=雨)≈0.46 | G i n i ( D , 温 度 = 冷 ) ≈ 0.45 Gini(D,温度=冷)\approx 0.45 Gini(D,温度=冷)≈0.45 |
在全部的特征中, G i n i ( D , 温 度 = 适 宜 ) ≈ 0.23 Gini(D,温度=适宜)\approx 0.23 Gini(D,温度=适宜)≈0.23 最小,所以当前已温度特征为最优特征,温度适宜为最优划分点。
使用 Numpy 计算。
(1)基尼指数计算函数
import numpy as np
def gini(nums):
"""
输入:
->nums:包含类别取值的列表
输出:
->gini:基尼指数
"""
# 获取列表类别的概率分布
probs = [nums.count(i)/len(nums) for i in set(nums)]
# 计算基尼指数
gini = sum([p*(1-p) for p in probs])
return gini
(2)天气条件下的基尼指数计算
import pandas as pd
df = pd.read_csv("./golf_data.csv")
# 其中 subset1,subset2 为根据天气特征晴和非晴划分之后的子集
subset1 = df[df["outlook"] == "sunny"]
subset2 = df[df["outlook"] != "sunny"]
# 计算基尼指数
gini_DA = len(subset1)/len(df)*gini(subset1["play"].tolist()) + \
len(subset2)/len(df)*gini(subset2["play"].tolist())
print(gini_DA)
ptint:0.3936507936507937
决策树构建
ID3
I D 3 ID3 ID3(Iterative Dichotomiser 3)3代迭代二叉树。其核心是基于信息增益递归地选择最优的特征构造决策树。
具体方法
首先预设一个决策树根节点,然后对于所有特征计算信息增益,选择一个信息增益最大的特征作为最优特征,根据该特征的不同取值建立子节点,接着对每个子节点递归地调用上述方法,直到信息增益很小或者没有特征可选为止,即可构建 I D 3 ID3 ID3 决策树。
给定训练集 D D D、特征集合 A A A 以及信息增益阈值 ε \varepsilon ε, I D 3 ID3 ID3 的算法算法流程:
(1)如果 D D D 中所有实例属于同一类别 C k C_k Ck,那么所构建的决策树 T T T 为单结点树,并且类 C k C_k Ck 即为该结点的类的标记。
(2)如果 T T T 不是单结点树,则计算特征集合 A A A 中各特征对 D D D 的信息增益,选择信息最大增益最大的特征 A g A_g Ag。
(3)如果 A g A_g Ag 的信息增益小于阈值 ε \varepsilon ε,则将 T T T 视为单结点树,并将 D D D 中所属数量最多的类 C k C_k Ck 作为该结点的类的标记并返回 T T T。
(4)否则,可对 A g A_g Ag 的每一个特征取值 a i a_i ai,按照 A g = a i A_g=a_i Ag=ai 将 D D D 划分为若干非空子集 D i D_i Di,已 D i D_i Di 中所属数量最多的类作为标记并构建子结点,由结点和子结点构成树 T T T 并返回。
(5)对第 i i i 个子节点,以 D i D_i Di 为训练集,以 A − A g A-A_g A−Ag 为特征集,递归的调用 ( 1 ) ∼ ( 4 ) (1)\sim(4) (1)∼(4) 步,即可得到决策树子树 T i T_i Ti 并返回。
基于 Numpy 实现
(1)信息熵计算函数
# 导入 numpy 库
import numpy as np
# 导入对数计算模块
from math import log
def entropy(ele):
"""
输入:包含类别取值的列表
输出:信息熵值
"""
# 计算列表中取值的概率分布
probs = [ele.count(i)/len(ele) for i in set(ele)]
# 计算信息熵
entropy = -sum(prob*log(prob,2) for prob in probs)
return entropy
(2)数据集划分函数
def df_split(df, col):
"""
输入:
df: 待划分的训练数据
col: 划分数据的依据特征
输出:
res_dict: 根据特征取值划分后的不同数据集字典
"""
# 获取依据特征的不同取值
unique_col_val = df[col].unique()
# 创建划分结果的数据框字典
res_dict = {elem:pd.DataFrame for elem in unique_col_val}
# 根据特征取值进行划分
for key in res_dict.keys():
res_dict[key] = df[:][df[col] == key]
return res_dict
(3)选择最优特征
# 根据训练集和标签选择信息增益最大的特征作为最优特征
def choose_best_feature(df, label):
"""
输入:
df: 待划分的训练数据
label: 训练标签
输出:
mas_value: 最大信息增益值
best_feature: 最优特征
max_splited: 根据最优特征划分后的数据字典
"""
# 计算训练标签的信息熵
entropy_D = entropy(df[label].tolist())
# 特征集
cols = [col for col in df.colums if col not in [label]]
# 初始化最大信息增益值、最优特征和划分后的数据集
max_value, best_feature = -999, None
max_splited = None
# 遍历特征并根据特征划分后的数据集
for col in cols:
# 根据当前特征取值划分后的数据集
splited_set = df_split(df, col)
# 初始化经验条件熵
entropy_DA = 0
# 对划分后的数据集遍历计算
for subset_col, subset in splited_set.items():
# 计算划分后的数据子集的标签信息熵
entropy_Di = entropy(subset[label].tolist())
# 计算当前特征的经验条件熵
entropy_DA += len(subset)/len(df) * entropy_Di
# 计算当前特征的信息增益
info_gain = entropu_D - entropy_DA
# 获取最大信息增益,并保存对应的特征和划分结果
if info_gain > max_value:
max_value, best_feature = info_gain, col
max_splited = splited_set
return max_value, best_feature, max_splited
(4)构建 I D 3 ID3 ID3 决策树
class ID3tree:
# 定义决策树结点类
class TreeNode:
# 定义树节点
def __init__(self, name):
self.name = name
self.connections = {}
# 定义树连接
def connect(self, label, node):
self.connections[label] = node
# 定义全局变量,包括数据集、特征集、标签和根节点
def __init__(self, df, label):
self.columns = df.columns
self.df = df
self.label = label
self.root = self.TreeNode("Root")
# 构建树的调用
def construct_tree(self):
self.construct(self.root, "", self.df, self.columns)
# 决策树构建方法
def construct(self, parent_node, parent_label, sub_df, columns):
# 选择最优特征
max_value, best_feature, max_splited = choose_best_feature(sub_df[columns], self.label)
# 如果选不到最优特征的,则构建单结点树
if not best_feature:
node = self.TreeNode(sub_df[self.label].iloc[0])
parent_node.connect(parent_label, node)
return
# 根据最优特征以及子结点构建树
node = self.TreeNode(best_feature)
parent_node.connect(parent_label, node)
# 以 A-Ag 为新的特征集
new_columns = [col for col in columns if col != best_feature]
# 递归地构建决策树
for splited_value, splited_data in max_splited.items():
self.construct(node, splited_value, splited_data, new_columns)
# 打印决策树
def print_tree(self, node, tabs):
print(tabs + node.name)
for connection, child_node in node.connections.items():
print(str(tabs) + "\t" + "(" + str(connection) + ")")
self.print_tree(child_node, tabs + "\t\t")
(5)ID3 决策树
import pandas as pd
# 载入数据
df = pd.read_csv("./golf_data.csv")
# 创建 ID3 实例模型
id3_tree = ID3tree(df, "play")
# 构建 ID3 决策树
id3_tree.construct_tree()
# 打印决策树
id3_tree.print_tree(id3_tree.root, "")
基于 sklearn 实现
- 希望没写错吧,应该是数据量太小了,所以准确率只有 0.4 0.4 0.4,甚至比直接猜还低。
import numpy as np
import pandas as pd
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
from sklearn import tree
# 载入数据
df = pd.read_csv('golf_data.csv')
# 对属性进行编码
encoder = preprocessing.LabelEncoder()
for i in range(0,df.shape[1]):
df[df.columns[i]] = encoder.fit_transform(df[df.columns[i]])
X = np.array(df[["humility","outlook","temp","windy"]])
y = df["play"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)
# 定义 ID3 模型(模型参数为:"entropy")
id3_tree = tree.DecisionTreeClassifier(criterion = "entropy", random_state = 30)
id3_tree.fit(X_train, y_train)
pre = id3_tree.predict(X_test)
print(y_test.values)
print(pre)
# 评分
score = id3_tree.score(X_test, y_test)
print(score)
# 画树
import graphviz
feature_name = ["湿度","天气","温度","是否有风"]
dot_data = tree.export_graphviz(id3_tree
,feature_names = feature_name
,class_names = ["去", "不去"]
,filled = True
,rounded = True
)
graph = graphviz.Source(dot_data)
graph
C4.5
C 4.5 C4.5 C4.5 与 I D 3 ID3 ID3 类似,不同之处在于 C 4.5 C4.5 C4.5 使用的是信息增益比的特征选择方法。
具体方法
给定训练集 D D D、特征集合 A A A 以及信息增益阈值 ε \varepsilon ε, I D 3 ID3 ID3 的算法算法流程:
(1)如果 D D D 中所有实例属于同一类别 C k C_k Ck,那么所构建的决策树 T T T 为单结点树,并且类 C k C_k Ck 即为该结点的类的标记。
(2)如果 T T T 不是单结点树,则计算特征集合 A A A 中各特征对 D D D 的信息增益比,选择信息最大增益比最大的特征 A g A_g Ag。
(3)如果 A g A_g Ag 的信息增益比小于阈值 ε \varepsilon ε,则将 T T T 视为单结点树,并将 D D D 中所属数量最多的类 C k C_k Ck 作为该结点的类的标记并返回 T T T。
(4)否则,可对 A g A_g Ag 的每一个特征取值 a i a_i ai,按照 A g = a i A_g=a_i Ag=ai 将 D D D 划分为若干非空子集 D i D_i Di,已 D i D_i Di 中所属数量最多的类作为标记并构建子结点,由结点和子结点构成树 T T T 并返回。
(5)对第 i i i 个子节点,以 D i D_i Di 为训练集,以 A − A g A-A_g A−Ag 为特征集,递归的调用 ( 1 ) ∼ ( 4 ) (1)\sim(4) (1)∼(4) 步,即可得到决策树子树 T i T_i Ti 并返回。
基于 Numpy 实现
将 I D 3 ID3 ID3 的选择最优特征使用这个替换就行了。
# 根据训练集和标签选择信息增益最大的特征作为最优特征
def choose_best_feature(df, label):
"""
输入:
df->待划分的训练数据
label->训练标签
输出:
mas_value->最大信息增益值
best_feature->最优特征
max_splited->根据最优特征划分后的数据字典
"""
# 计算训练标签的信息熵
entropy_D = entropy(df[label].tolist())
# 特征集
cols = [col for col in df.columns if col not in [label]]
# 初始化最大信息增益值、最优特征和划分后的数据集
max_value, best_feature = -999, None
max_splited = None
# 遍历特征并根据特征划分后的数据集
for col in cols:
# 根据当前特征取值划分后的数据集
splited_set = df_split(df, col)
# 初始化经验条件熵
entropy_DA = 0
# 对划分后的数据集遍历计算
for subset_col, subset in splited_set.items():
# 计算划分后的数据子集的标签信息熵
entropy_Di = entropy(subset[label].tolist())
# 计算当前特征的经验条件熵
entropy_DA += len(subset)/len(df) * entropy_Di
# 计算当前特征的信息增益
info_gain = entropy_D - entropy_DA
# 信息增益率
entropy_A = entropy(df[label].tolist())
if(entropy_A != 0):
info_gain_rate = info_gain/entropy_A
else :
info_gain_rate = 0;
# 获取最大信息增益,并保存对应的特征和划分结果
#if info_gain > max_value:
# max_value, best_feature = info_gain, col
# max_splited = splited_set
# 获取最大信息增益比,并保存对应的特征和划分结果
if info_gain_rate >max_value:
max_value, best_feature = info_gain_rate, col
max_splited = splited_set
return max_value, best_feature, max_splited
CART
CART 算法的全称为分类与回归树(classification and regression tree),CART 即可以用于分类,也可以用于回归,这是与前两种方法的主要区别之一。除此之外,CART 算法的特征选择方法不再基于信息增益或信息增益率,而是基于基尼指数。最后 CART 算法不仅包括决策树的生成算法,还包括决策树剪枝算法。
CART 算法可以理解为在给定随机变量 X X X 的基础下输出随机变量 Y Y Y 的条件概率分布的学习算法。CART 生成的决策树都是严格的二叉树,其内部结点取值为 “是” 和 “否”,这种结点划分方法等价于递归的二分每个特征,将特征空间划分为有限个单元,并在这些单元上确定预测的概率分布,即前述预测条件概率分布。
CART分类树
CART 分类树生成算法是基于最小基尼指数递归地选择最优特征,并确定最优特征的最优二值划分点。
给定训练集 D D D、特征集合 A A A 以及信息增益阈值 ε \varepsilon ε, C A R T CART CART 分类树算法流程:
(1)对于每个特征 a a a 及其所有取值 a i a_i ai,根据 a = a i a=a_i a=ai 将数据集划分为 D 1 D1 D1 和 D 2 D_2 D2 两个部分,并计算 a = a i a=a_i a=ai 时的基尼指数。
(2)取基尼指数最小的特征以及对应的划分点作为最优特征和最优划分点。
(3)对两个子节点递归地调用 ( 1 ) (1) (1) 和 ( 2 ) (2) (2)。
CART回归树
假设训练输入 X X X 和输出 Y Y Y,给定训练集 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x k , y k ) D={(x_1,y_1),(x_2,y_2),\cdots,(x_k,y_k)} D=(x1,y1),(x2,y2),⋯,(xk,yk),且每个划分单元都有一个输出权重 c i c_i ci,那么回归树模型可以表示为:
f ( x ) = ∑ i = 1 k c i I ( x ∈ R k ) (14) f(x)=\sum_{i=1}^{k}c_iI(x\in R_k) \tag{14} f(x)=i=1∑kciI(x∈Rk)(14)
和线性回归一样,回归树模型训练的目的同样是最小化均方损失,求最优输出权重 c ^ i \hat{c}_i c^i。最优输出权重 c ^ i \hat{c}_i c^i 可以通过每个单元上所有输入实例 x i x_i xi 对应的输出值 y i y_i yi 的均值来确定。
c ^ i = a v e r a g e ( y i ∣ x i ∈ R i ) (15) \hat{c}_i=average(y_i|x_i\in R_i) \tag{15} c^i=average(yi∣xi∈Ri)(15)
假设随机选取第 j j j 个特征 x ( j ) x^{(j)} x(j) 及其对应的某个取值 s s s,将其作为划分特征和划分点,同时定义两个区域:
R 1 ( j , s ) = { x ∣ x ( j ) ≤ s } ; R 2 ( j , s ) = { x ∣ x ( j ) > s } (16) R_1(j,s)=\{x|x^{(j)}\le s\};R_2(j,s)=\{x|x^{(j)}> s\} \tag{16} R1(j,s)={x∣x(j)≤s};R2(j,s)={x∣x(j)>s}(16)
然后求解:
m i n j s [ m i n c 1 ∑ x i ∈ R 1 ( j , s ) ( y i − c i ) 2 + m i n c 2 ∑ x i ∈ R 2 ( j , s ) ( y i − c i ) 2 ] (17) min_{js}\Bigg[min_{c_1}\sum_{x_i\in R_1(j,s)}(y_i-c_i)^2+min_{c_2}\sum_{x_i\in R_2(j,s)}(y_i-c_i)^2\Bigg] \tag{17} minjs[minc1xi∈R1(j,s)∑(yi−ci)2+minc2xi∈R2(j,s)∑(yi−ci)2](17)
求解上式即可得到输入特征 j j j 和最优划分点 s s s。按照上述平方误差最小准则可以求的全局最优特征和取值,并据此将特征空间划分为两个子区域,对每个子区域重复前面的划分过程,即可构建回归树。
CART回归树生成算法。
(1)根据上式子求解最优特征 j j j 和最优划分点 s s s,遍历训练集所有特征,对固定划分特征扫表划分点 s s s,可求得 式子 最小值。
(2)通过式 ( 15 ) (15) (15) 和式 ( 16 ) (16) (16) 确定的最优 ( j , s ) (j,s) (j,s) 来划分特征空间区域并决定相应的输出权重。
(3)对划分的两个子树递归调用 ( 1 ) (1) (1) 和 ( 2 ) (2) (2)。
(4)将特征空间划分为 k k k 个单元 R 1 , R 2 , ⋯ , R k R_1,R_2,\cdots,R_k R1,R2,⋯,Rk,生成回归树。
基于 Numpy 实现
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, mean_squared_error
(1)定义树节点
class TreeNode():
def __init__(self
, feature_idx = None
, threshold = None
, leaf_value = None
, left_branch = None
, right_branch = None
):
# 特征索引
self.feature_idx = feature_idx
# 特征划分阈值
self.threshold = threshold
# 叶子节点取值
self.leaf_value = leaf_value
# 左子树
self.left_branch = left_branch
# 右子树
self.right_branch = right_branch
(2)划分函数、基尼指数计算函数
# 定义二叉特征划分函数
def feature_split(X, feature_idx, threshold):
split_func = None
if isinstance(threshold, int) or isinstance(threshold, float):
split_func = lambda sample: sample[feature_idx] >= threshold
else:
split_func = lambda sample: sample[feature_idx] == threshold
X_left = np.array([sample for sample in X if split_func(sample)])
X_right = np.array([sample for sample in X if not split_func(sample)])
return np.array([X_left, X_right])
# 计算基尼指数
def calculate_gini(y):
# 将数组转化为列表
y = y.tolist()
probs = [y.count(i)/len(y) for i in np.unique(y)]
gini = sum([p*(1-p) for p in probs])
return gini
(3)定义二叉决策树
class BinaryDecisionTree(object):
# 决策树初始化
def __init__(self
, min_samples_split = 2
, min_gini_impurity = 999
, max_depth = float("inf")
, loss = None
):
# 根结点
self.root = None
# 节点最小分裂样本数
self.min_samples_split = min_samples_split
# 节点初始化基尼不纯度
self.mini_gini_impurity = min_gini_impurity
# 树最大深度
self.max_depth = max_depth
# 基尼不纯度计算函数
self.gini_impurity_calculation = None
# 叶子节点值预测函数
self._leaf_value_calculation = None
# 损失函数
self.loss = loss
# 决策树训练
def fit(self, X, y, loss=None):
# 递归构建决策树
self.root = self._build_tree(X, y)
self.loss = None
# 决策树构建函数
def _build_tree(self, X, y, current_depth = 0):
# 初始化最小基尼不纯度
init_gini_impurity = 999
# 初始化最佳特征索引和阈值
best_criteria = None
# 初始化数据子集
best_sets = None
# 合并输入和标签
Xy = np.concatenate((X, y), axis=1)
# 获取样本数和特征数
n_samples, n_features = X.shape
# 设定决策树构建条件
# 训练样本数量大于节点最小分裂样本数且当前树深度小于最大深度
if n_samples >= self.min_samples_split and current_depth <= self.max_depth:
# 遍历计算每个特征的基尼不纯度
for feature_idx in range(n_features):
# 获取第i特征的所有取值
feature_values = np.expand_dims(X[:, feature_idx], axis=1)
# 获取第i个特征的唯一取值
unique_values = np.unique(feature_values)
# 遍历取值并寻找最佳特征分裂阈值
for threshold in unique_values:
# 特征节点二叉分裂
Xy1, Xy2 = feature_split(Xy, feature_idx, threshold)
# 如果分裂后的子集大小都不为0
if len(Xy1) > 0 and len(Xy2) > 0:
# 获取两个子集的标签值
y1 = Xy1[:, n_features:]
y2 = Xy2[:, n_features:]
# 计算基尼不纯度
impurity = self.impurity_calculation(y, y1, y2)
# 获取最小基尼不纯度
# 最佳特征索引和分裂阈值
if impurity < init_gini_impurity:
init_gini_impurity = impurity
best_criteria = {"feature_idx": feature_idx, "threshold": threshold}
best_sets = {
"leftX": Xy1[:, :n_features],
"lefty": Xy1[:, n_features:],
"rightX": Xy2[:, :n_features],
"righty": Xy2[:, n_features:]
}
# 如果计算的最小不纯度小于设定的最小不纯度
if init_gini_impurity < self.mini_gini_impurity:
# 分别构建左右子树
left_branch = self._build_tree(best_sets["leftX"], best_sets["lefty"], current_depth + 1)
right_branch = self._build_tree(best_sets["rightX"], best_sets["righty"], current_depth + 1)
return TreeNode(feature_idx = best_criteria["feature_idx"]
, threshold = best_criteria["threshold"]
, left_branch = left_branch
, right_branch = right_branch
)
# 计算叶子计算取值
leaf_value = self._leaf_value_calculation(y)
return TreeNode(leaf_value=leaf_value)
# 定义二叉树值预测函数
def predict_value(self, x, tree=None):
if tree is None:
tree = self.root
# 如果叶子节点已有值,则直接返回已有值
if tree.leaf_value is not None:
return tree.leaf_value
# 选择特征并获取特征值
feature_value = x[tree.feature_idx]
# 判断落入左子树还是右子树
branch = tree.right_branch
if isinstance(feature_value, int) or isinstance(feature_value, float):
if feature_value >= tree.threshold:
branch = tree.left_branch
elif feature_value == tree.threshold:
branch = tree.left_branch
# 测试子集
return self.predict_value(x, branch)
# 数据集预测函数
def predict(self, X):
y_pred = [self.predict_value(sample) for sample in X]
return y_pred
分类树
(1)分类树定义
class ClassificationTree(BinaryDecisionTree):
# 定义基尼不纯度计算过程
def _calculate_gini_impurity(self, y, y1, y2):
p = len(y1) / len(y)
gini = calculate_gini(y)
gini_impurity = p * calculate_gini(y1) + (1-p) * calculate_gini(y2)
return gini_impurity
# 多数投票
def _majority_vote(self, y):
most_common = None
max_count = 0
for label in np.unique(y):
# 统计多数
count = len(y[y == label])
if count > max_count:
most_common = label
max_count = count
return most_common
# 分类树拟合
def fit(self, X, y):
self.impurity_calculation = self._calculate_gini_impurity
self._leaf_value_calculation = self._majority_vote
super(ClassificationTree, self).fit(X, y)
(2)分类树测试
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
data = datasets.load_iris()
X, y = data.data, data.target
y = y.reshape((-1, 1))
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3)
# 创建分类树模型实例
clf = ClassificationTree()
# 分类树训练
clf.fit(X_train, y_train)
# 分类树预测
y_pred = clf.predict(X_test)
print(y_test.T)
print(y_pred)
回归树
(1)回归树定义
class RegressionTree(BinaryDecisionTree):
def _calculate_variance_reduction(self, y, y1, y2):
var_tot = np.var(y, axis=0)
var_y1 = np.var(y1, axis=0)
var_y2 = np.var(y2, axis=0)
frac_1 = len(y1) / len(y)
frac_2 = len(y2) / len(y)
# 计算方差减少量
variance_reduction = var_tot - (frac_1 * var_y1 + frac_2 * var_y2)
return sum(variance_reduction)
# 节点值取平均
def _mean_of_y(self, y):
value = np.mean(y, axis=0)
return value if len(value) > 1 else value[0]
def fit(self, X, y):
self.impurity_calculation = self._calculate_variance_reduction
self._leaf_value_calculation = self._mean_of_y
super(RegressionTree, self).fit(X, y)
(2)回归树测试
# 波士顿房价
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 获取输入和标签
X, y = load_boston(return_X_y = True)
y = y.reshape((-1, 1))
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3)
# 定义回归模型
reg = RegressionTree()
# 模型训练
reg.fit(X_train, y_train)
# 模型预测
y_pred = reg.predict(X_test)
# 均方误差
mse = mean_squared_error(y_test, y_pred)
print("MES of CRAT regression tree based on Numpy: ", mse)
基于 sklearn 实现
- 分类树
import numpy as np
import pandas as pd
import graphviz
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import tree
from sklearn.metrics import accuracy_score
# 按 7:3 划分训练集,测试集
data = datasets.load_iris()
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size = 0.3)
# 定义模型
clf = tree.DecisionTreeClassifier()
# 模型训练
clf.fit(X_train, y_train)
# 模型预测
y_pred = clf.predict(X_test)
# accuracy
print(accuracy_score(y_test, y_pred))
# 画图
dot_data = tree.export_graphviz(clf
, feature_names = data.feature_names
, class_names = data.target_names
, filled = True
, rounded = True
)
graph = graphviz.Source(dot_data)
graph
- 回归树
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
# 按 7:3 划分训练集,测试集
data = load_boston()
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size = 0.3)
# 定义模型
reg = DecisionTreeRegressor()
# 模型训练
reg.fit(X_train, y_train)
# 模型预测
y_pred = reg.predict(X_test)
# mse
mse = mean_squared_error(y_test, y_pred)
print("Mean Squared Error:", mse)
# 画图
plt.plot(y_test, label = 'target')
plt.plot(y_pred, label = 'pred')
plt.legend()
plt.show()
决策树剪枝
决策树生成算法递归的产生决策树,往往生成的树是十分巨大,这很容易导致过拟合。
决策树剪枝一般包含两种方法:①预剪枝,②后剪枝。
(1)预剪枝
在决策树生成过程中提前停止树的生长。在决策树结点分裂之前,计算当前结点划分能否提升模型泛华能力,如果不能则该结点停止生长。预剪枝方法简单高效,适用于大规模问题求解。
预剪枝思想主要运用于集成学习模型中。但是提前停止生长也可能导致决策树欠拟合的发生。
(2)后剪枝
极小化决策树整体损失函数。其中
学习的目标是找到一颗能够最大可能正确分类的决策树,但是为了保证泛化性,不出现过拟合。决策树模型在正则化参数的同时最小化经验误差。假设一颗决策树 T T T 的叶子结点个数为 ∣ T ∣ |T| ∣T∣, t t t 为树 T T T 的叶子结点,每个叶子结点有 N t N_t Nt 个样本,假设 k k k 类的样本有 N t k N_{tk} Ntk 个,其中 k = 1 , 2 , ⋯ , K k=1,2,\cdots,K k=1,2,⋯,K, H t ( T ) H_t(T) Ht(T) 为叶子结点上的经验熵, a ≥ 0 a\ge0 a≥0 为正则化参数,那么觉得是学习的损失函数可表示为:
L ( ) L() L()
尾注
参考
[1]鲁伟.机器学习-公式推导与代码实现[M].北京:人民邮电出版社,2022.
[2]周志华.机器学习[M].北京:清华大学出版社,2016.
[3]谢文睿,秦川.机器学习公式详解[M].北京:人民邮电出版社,2022.
[4]李航.统计学习方法[M].北京:清华大学出版社,2019.
关于基尼系数和基尼指数(基尼不纯度)
本篇文章都是使用基尼指,关于基尼系数和基尼指数可以看下面这几篇文章。
【AI基础】基尼系数与基尼不纯度 - 知乎 (zhihu.com)
基尼不纯度 - 面试天下网 (mstx.cn)