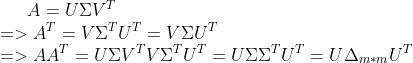SVD分解

0.背景

在线性代数领域，SVD分解常用的场景是对长方形矩阵的分解；而在机器学习领域，SVD可用于降维处理；但是这么说实在是太抽象了，我们从一个例子出发来重新看一下SVD到底是一个啥玩意儿叭

1.特征值与特征向量

其中是一个n*n的矩阵，是的一个特征值，是一个属于特征值的n*1的特征向量。

2.特征值分解

根据上式，可以推出：

可知，我们可以用特征值+特征向量来替代原矩阵。

3.奇异值与奇异值分解(SVD)

上面所述的特征值分解仅仅适用于方阵，那么对于长方阵要怎么处理？我们有没有办法将长方阵转换到方阵上呢？做了再说。我们就先定义一种分解，假设有

为了运算方便(下面就可以看到)，同时规定除对角线以外的元素都是0，对角线元素称为奇异值(类似特征值)，。

为了仿照特征值的求解方法，我们需要构造一个方阵，可以想到，那么使用这个新矩阵R来求解特征值会发生什么呢？即有

仿照上面特征值分解的方式将特征向量组合，可以得到矩阵V，称这些特征向量为右奇异向量。同理，构造，再解一批特征向量

组合这些新特征向量可得左奇异矩阵U。

根据条件我们来处理一下：

 

同理有

由此一来，可以证明奇异值满足。

值得注意的是，和的非零值相同，即需证明与：

3.1.首先证明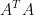与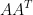拥有相同的秩

设线性方程组，左乘则有，即的解也是的解。

对于，左乘则，又因为是一个向量，相当于是向量自己和自己内积，即模平方为0，因此可以推出向量是0向量，因此。

所以可以证明与有相同的解空间，也就可得，又有，因此可知。 

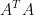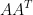3.2.然后证明与的非零特征值相同

假设是的属于特征值的特征向量，所以有，两边同乘，有，故有。故可得 与的非零特征值相同。

4.SVD在机器学习领域中的应用

在机器学习领域，我们常常遇到的问题是，数据以 样本 * 特征 的形式存储为一个2维矩阵，而这其中，往往存在稀疏性，即样本量很大，特征维度也很多，但是对于不同的人而言，他们的特征表达可能都是非常稀疏的。

用特征向量的形式表示来说，可能样本A、B各自的特征向量如下：

0这种量化值，实际上并不包含信息，至于为什么，我的个人理解是：

我们在机器学习领域使用特征的构建表达时使用的基本公式为Wx+b，试想x=0的时候，相当于只有偏置，特征本身并没有信息可以代入。

因此矩阵虽然很大，但是包含的信息量相比矩阵规模来说显得非常少，因此能不能通过提取重要信息的方式尝试对矩阵做一个降维呢？答案当然是可以的哇。

为了讲述上面所说的矩阵降维，我们回顾一下特征值分解，在方阵的情况下，若可以分解，则有

其中由A的特征向量和特征值可以构成和。

那么搬到长方阵中，我们使用SVD，可以找到一组等式使得

这样还不够，因为我们发现这样做，得到的三个矩阵，累积的维度比原来的还大，这怎么降维呢？别急，我们回到特征值分解，在特征值分解中，需要求出原矩阵的特征值，但是实际上原矩阵的特征值有些可能非常小，这里就不得不提一下特征值与特征向量的含义：

特征值：用于表示变化幅度

特征向量：用于表示变化方向

这一点可以看公式，特征值特征向量的定义可以由下式表示：

特征值的大小表示了信息量，因此我们可以只提取原始矩阵中的部分信息即特征值较大的那些对应的信息，假设我们只提取k个最大的特征值对应的信息，那么上述公式就变为：

一般来说信息会集中在前面比较大的特征值上，而在SVD中，奇异值的大小降低得非常快，因此我们可以就取部分的奇异值及其对应的奇异向量来近似替代原矩阵做一个降维，这就是整个SVD做降维的思路。