使用keras里面的lstm进行时间序列预测_【重温序列模型】再回首DeepLearning遇见了LSTM和GRU...
昵称 | Miracle8070
研究 | 时空序列预测与数据挖掘
出品 | AI蜗牛车
1. 写在前面
学习时空序列, 会需要很多序列模型的相关知识,所以借着这次机会想重新学习一下深度学习里面的序列模型模块,并做一个知识的梳理,主要会包括RNN, LSTM和GRU, seq2seq, embedding和Attention。由于之前学习的时候, 没有深入到具体细节的研究, 所以导致现在复现一些网络或者学习深度学习进阶知识的时候会出现一些问题,于是想再重温一下, 并做一个总结, 相信每一次学习都会有新的收获。这次的整理主要是知识的串联和查缺补漏(可能不会涉及到太基础的内容), 所以既会恍如初见也会似曾相识,这样才更有意思,哈哈。我们一起来重温基础吧。
这一部分每篇可能会比较长,因为想还是尽量通俗易懂且全面,所以开篇之前会给出简介,方便大家根据自己已掌握的知识进行查缺补漏。
再回首DeepLearning遇见了LSTM和GRU,这篇文章基于前面的重温循环神经网络(RNN), 通过前面的分析, 我们已经知道了RNN中的梯度消失和爆炸现在究竟是怎么回事并且也知道了引起梯度消失和爆炸的原因, 而又由于梯度消失, 导致了RNN并不擅长捕捉序列的长期关联, 所以基于这两个问题, 导致现在RNN使用的并不是太多, 而是使用它的一些变体, 比如LSTM, GRU这些,所以这篇文章就主要围绕着这两个变体进行展开。
首先, 我们先从LSTM开始, 先看一下LSTM和RNN的不同, 然后整理LSTM的工作原理和计算细节, 然后基于这个原理分析一下LSTM是如何解决RNN存在的两个问题的,为了更方便理解LSTM底层,依然是基于numpy实现一下LSTM的前向传播过程,明白了底层逻辑,那么LSTM到底如何在实际中使用?这里会简单介绍一下keras里面LSTM层的细节, 最后再整理GRU这块, 这可以说是LSTM的一种简化版, 那么到底是如何简化的, 与LSTM又会有哪些不同? 这篇文章会一一进行剖析。
大纲如下:
- RNN梯度消失怎么破? LSTM来了
- LSTM的工作原理和计算细节
- LSTM是如何解决RNN存在的梯度消失问题的
- LSTM前向传播的numpy实现及keras中LSTM层简单介绍
- LSTM的变体之GRU一些细节
- 总结
2. RNN梯度消失怎么破? LSTM来了
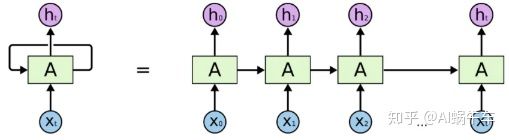
上面文章提到过, 循环神经网络(Recurrent Neural Network,RNN)是一种用于处理序列数据的神经网络。相比一般的神经网络来说,他能够处理序列变化的数据。比如某个单词的意思会因为上文提到的内容不同而有不同的含义,RNN就能够很好地解决这类问题。下面再来个RNN的图回顾一下(会发现和之前的图又是不一样, 好多种画法, 但是万变不离其宗, 原理不会变,哈哈):
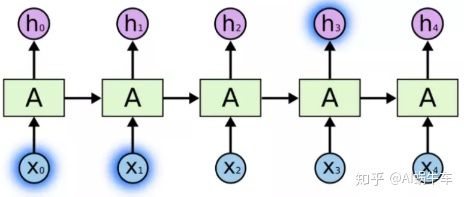
上一篇文章已经详细分析了这种网络的工作原理和计算方面的细节, 这里就不再过多赘述, 这里看一点新的东西, 就是序列依赖的问题, 上一篇文章中只是提到了循环网络一个很重要的作用就是能够捕捉序列之间的依赖关系, 而原理就是RNN在前向传播的时候时间步之间有隐藏状态信息的传递, 这样反向传播修改参数的时候, 前面时刻的一些序列信息会起到一定的作用,从而使得后面某个时刻的状态会捕捉到前面时刻的一些信息。 这在语言模型中非常常见。
比如我有个语言模型, 该模型根据前面的词语来预测下一个单词要预测一句话中的一部分, 如果我们试图预测“the clouds are in the sky”的最后一个单词, 这时候模型会预测出sky, 因为RNN会利用过去的历史信息clouds
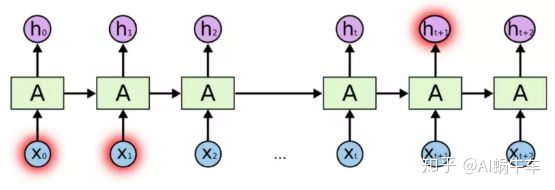
这是一种局部的依赖, 即在相关信息和需要该信息的距离较近的时候,RNN往往工作的效果还可以, 但如果是吴恩达老师举得那个例子:The cat, which already ate......., was full. 如果是要预测后面的这个was, 我们的语言模型这时候得考虑更多的上下文信息, 就不能是单单局部的信息了, 得需要从最开始获取cat的信息, 这种情况就属于相关信息和需要该信息的地方距离非常远。就是下面这种情况:
这时候, 我们的RNN表现的就不是那么出色了, 至于原因, 上一篇文章中我们分析了一点, 很重要的一点就是梯度的消失, 也就是时间步一旦很长, 就会出现连乘现象, 在反向传播的时候,这种连乘很容易会导致梯度消失, 一旦梯度消失, 后面的参数更新就无法再获取到前面时刻的关键信息,所以“长依赖”这个问题, 在RNN中是没法很好处理的。
那么, LSTM就来了, 这个东西其实不是最新的了,1997年的时候就引入了, 并且在各种各样的工作中工作效果不错,也广泛被使用, 虽然现在可能是Attention的天下了,甚至超越了LSTM, 但是LSTM依然可以解决很多的问题,是一个非常有力的工具,并且学习好LSTM, 对于理解Attention可能也会起到帮助, 总之,我觉得LSTM是肯定需要掌握的,哈哈。
LSTM的全称是Long short-term memory(长短期记忆), 是一种特殊的RNN网络, 该网络的设计是为了解决RNN不能解决的长依赖问题, 所以首先知道它是干啥用的? 那么它是如何做到的呢? 那么我们就需要对比一下LSTM和RNN的结构, 看看它到底改了什么东西才变得这么强大的呢?
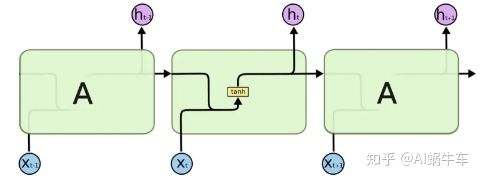
循环神经网络都具有神经网络的重复模块链的形式, 标准的RNN中,该重复模块将具有非常简单的结构,例如单个tanh层。标准的RNN网络如下图所示
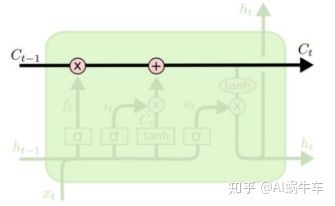
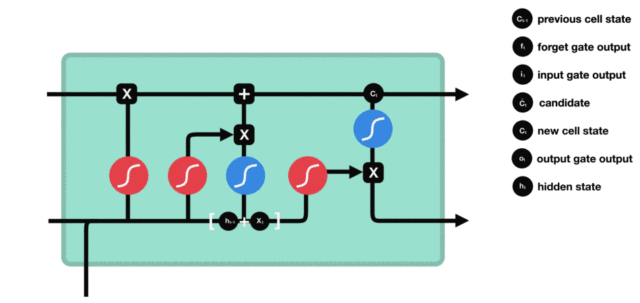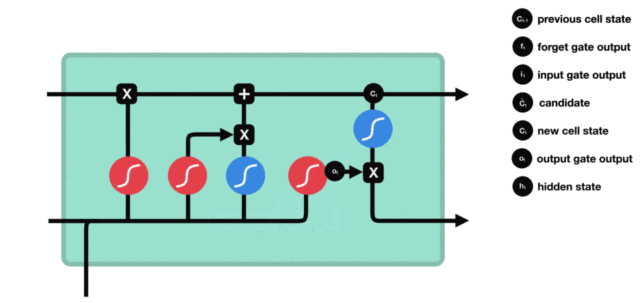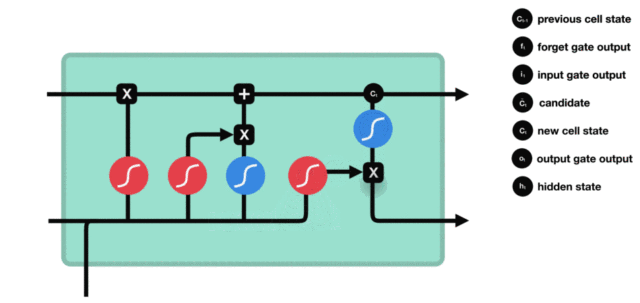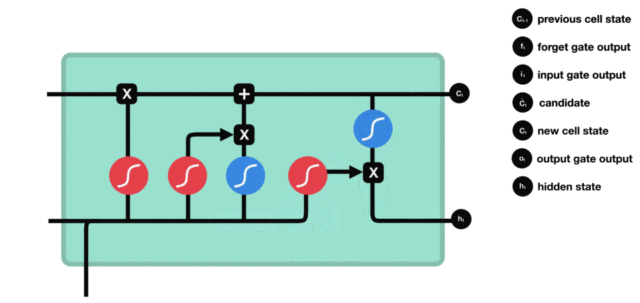
而LSTM既然是RNN网络, 那么也是采用的这种链式结构, 而与RNN不同的是每一个单元内部的运算逻辑, 下面先宏观上看一个LSTM的结构图, 在后面的运算细节那更能够看出这种运算逻辑:
很明显可以看到, LSTM与RNN相比,其实整体链式结构是没有改变的, 改变的是每个单元的内部的计算逻辑, LSTM这里变得复杂了起来, 而正式因为这种复杂, 才使得LSTM解决了RNN解决不了的问题, 比如梯度消失, 比如长期依赖。
下面就看看LSTM的原理和计算细节。
3. LSTM的工作原理和计算细节
所谓LSTM的工作原理,LSTM其实是在做一个这样的事情, 先尝试白话的描述一下, 然后再分析它是怎么实现。
我们前面说过,LSTM要解决的问题就是一种长期依赖问题, 也就是如果序列长度很长, 后面的序列就无法回忆起前面时刻序列的信息, 这样就很容易导致后面序列的预测出现错误,就跟人大脑一样, 如果时间很长, 就会出现遗忘一样, 记不清之前的一些事情,不利于后面的决策了。而出现这种情况的原因,就是我们在记忆的过程中, 干扰信息太多,记住了一些对后面决策没有用的东西, 时间一长, 反而把对后面决策有用的东西也忘掉了。
RNN其实也是一样, 普通的RNN后面更新的时候, 要回忆前面所有时刻的序列信息,往往就导致回忆不起来(梯度消失), 而我们知道, 对于未来做某个决策的时候, 我们并不需要回忆前面发生过的所有的事情,同理,对于RNN来说, 我要预测的这个单词需要考虑的上下文也并不是前面所有序列都对我当前的预测有用, 就比如上面的那个例子, 我要预测was, 我只需要最前面的cat即可, 中间那一串which巴拉巴拉的, 对我的预测没有用, 所以我预测was根本没有必要记住which的这些信息, 只需要记住cat即可, 这个在普通的RNN里面是没法做到的(不懂得可以看看它的前向传播过程), 它根本没有机会做出选择记忆, 而LSTM的核心,就是它比RNN, 多了一个可选择性的记忆cell, 在LSTM的每个时间步里面,都有一个记忆cell,这个东西就仿佛给与了LSTM记忆功能, 使得LSTM有能力自由选择每个时间步里面记忆的内容, 如果感觉当前状态信息很重要, 那么我就记住它, 如果感觉当前信息不重要, 那么我就不记, 继续保留前一时刻传递过来的状态, 比如cat的那个, 在cat的时刻,我把这个状态的信息保留下来, 而像which那些, 我不保留,这样was的时候就很容易看到cat这个状态的信息,并基于这个信息更新, 这样就能够进行长期依赖的学习了。
上面就是LSTM一个宏观工作原理的体现, 当然还有一些细节,比如这个记忆是怎么进行选择的, 这个记忆是怎么在时间步中传递的, 又是怎么保持的等, 下面从数学的角度详细的说说:
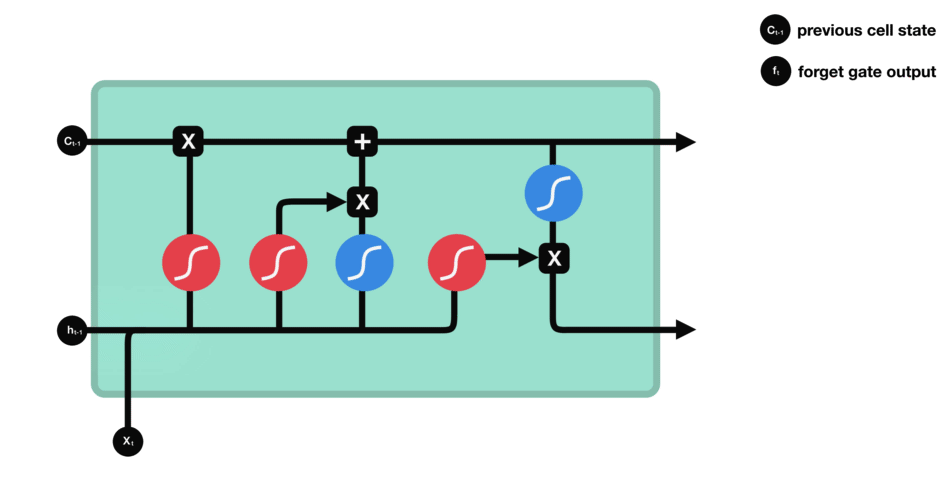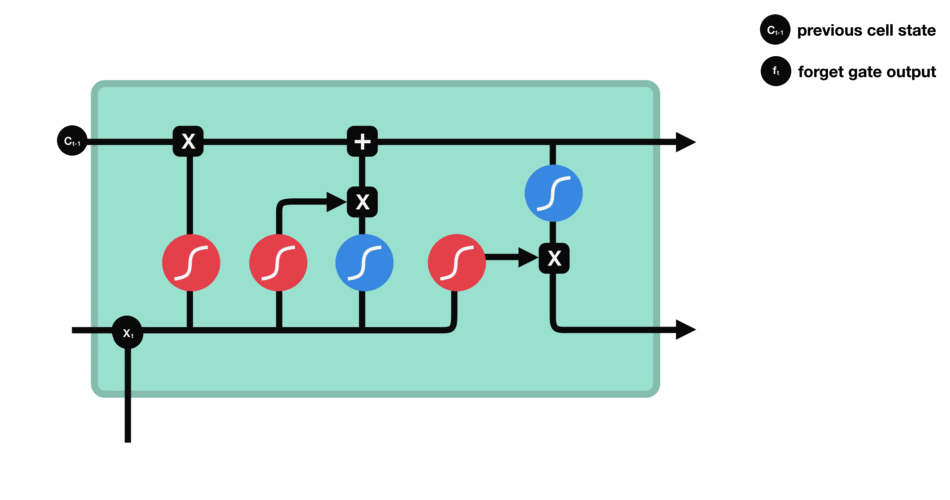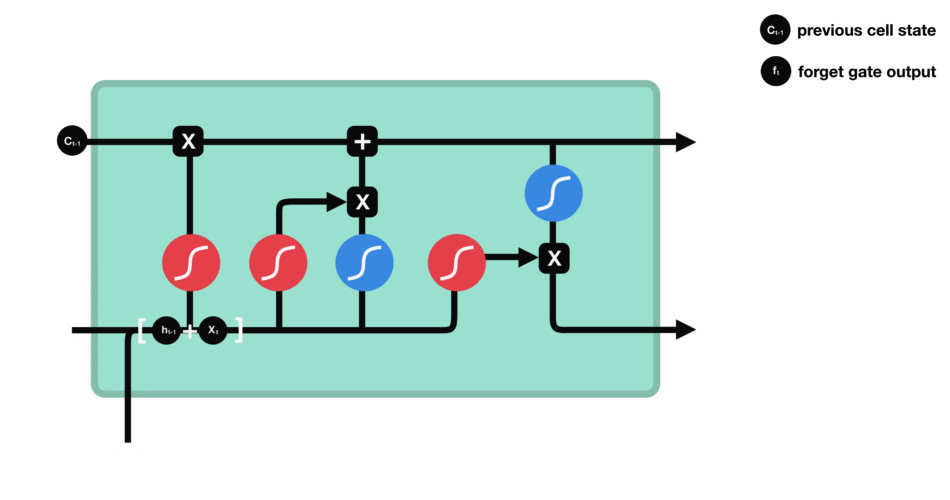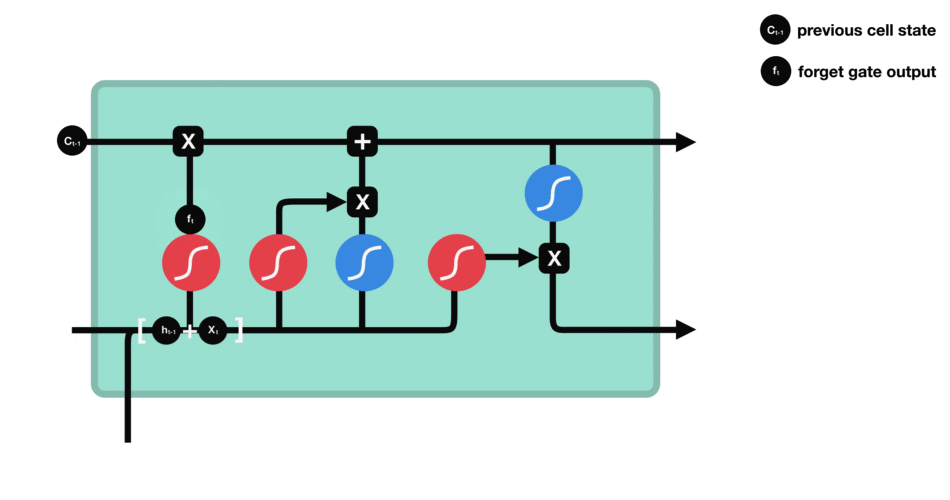
首先, 是那条记忆线到底在单元里面长什么样子:
LSTM的关键就是每个时间步之间除了隐藏状态
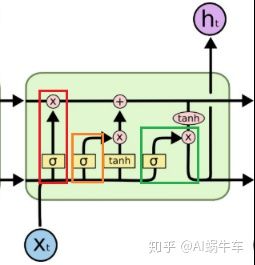
那么, LSTM是怎么做到自由选择记忆的东西的呢?这个就是LSTM里面那几个门发生的作用了, LSTM的cell状态存储是由被称为门的结构精细控制, 门是一种让信息可选地通过的方法。它们由一个sigmoid神经网络层和一个点乘操作组成。
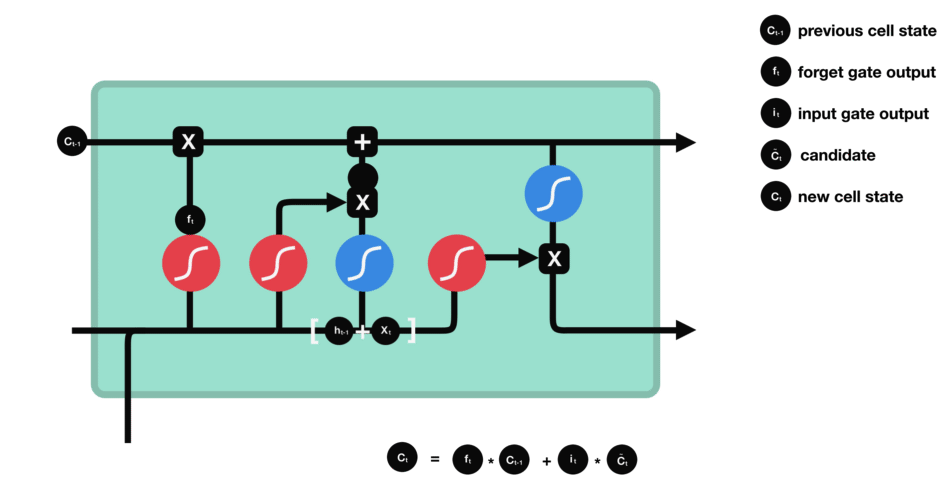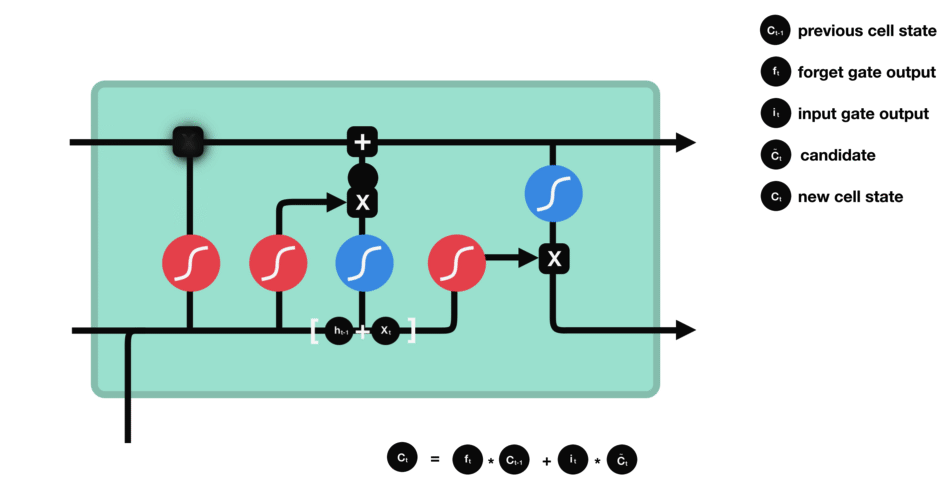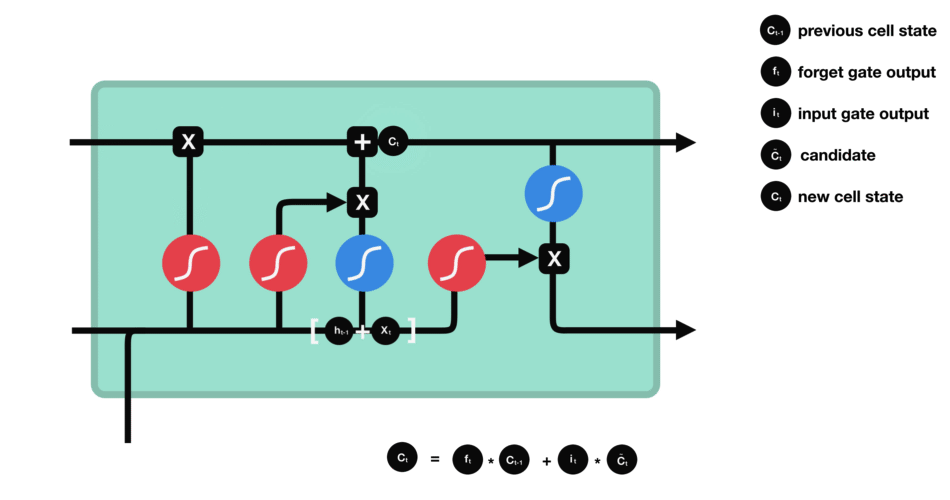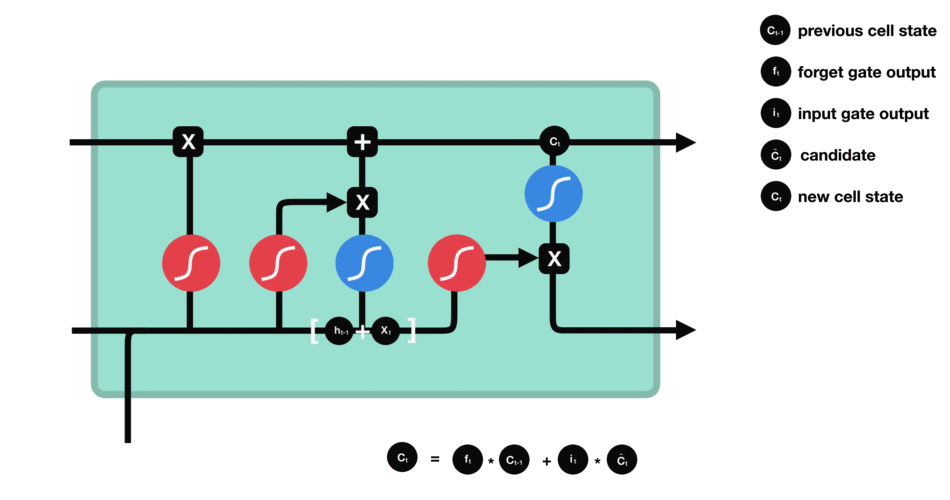
这里我标出来了, 看到这三个门了吗?那么就看看这三个门是如何起作用的, 首先, 我们解决另一个问题,就是cell里面到底存储的是什么东西, 看个图:
看上面这个图, 右边是
那么上面既然提到了
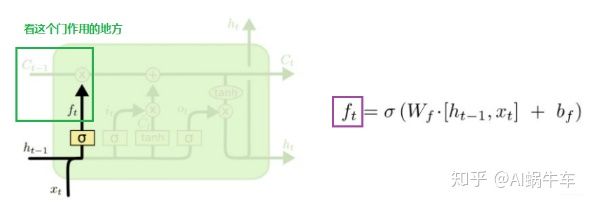
最左边这个叫做遗忘门(forget gate), 这个门决定着我们还需不需要记住前面状态的信息,即当前时刻的记忆状态有多少是来自于前面的记忆,比如对于一个基于上文预测最后一个词的语言模型。cell的状态可能包含当前主题的信息,来预测下一个准确的词。而当我们得到一个新的语言主题的时候,我们会想要遗忘旧的主题的记忆,应用新的语言主题的信息来预测准确的词。 右边是它的计算公式, 输入是
右边的一个门, 如下图:
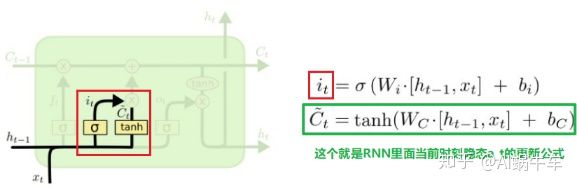
这个门叫做输入门或者更新门, 名字不重要, 干什么才是重要的, 这个门就是控制当前时刻的记忆有多少会来自于当前时刻的输入本身, 因为这个
只不过LSTM这里是将前面的那个加法改成了向量乘积的形式, 所以之类就很容易理解这个
所以LSTM这个名字可能看起来很吓人, 但可能是一个纸老虎。 依然是看一下运算过程:
通过上面的两个门,我们就可以把cell更新到一个我们想要的状态了,
但是光更新这个东西是没有意义的啊, 因为我们分析了was这个时候, 要记住cat的状态, 但记住的目的是要进行预测, 所以说我们的cell是为当前时刻的输出服务的。
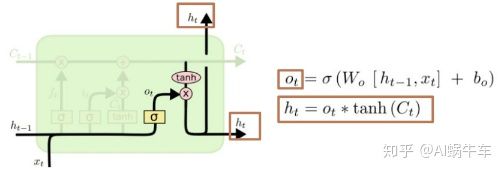
下面就看看输出部分到底是个啥?
这才是LSTM自由选择记忆之后的目的, 就是为了能有一个更好的输出。 这里首先是一个输出门, 依然是一个sigmoid, 取值0-1, 这个是控制我们的输出有多少是来自于我们的记忆,并不一定是全部的记忆哦。 使得LSTM更灵活了,连输出都可以进行选择了。这个意思差不多就是虽然我权衡了一下前面的状态信息和当前的状态信息, 更新了我的记忆, 但是这个记忆我不一定要全用上, 用一部分就可以搞定当前的预测。 并且如果我发现我更新的记忆对当前的预测并没有用, 反而会效果更差,这时候我还可以选择不用这个记忆, 所以非常的灵活。
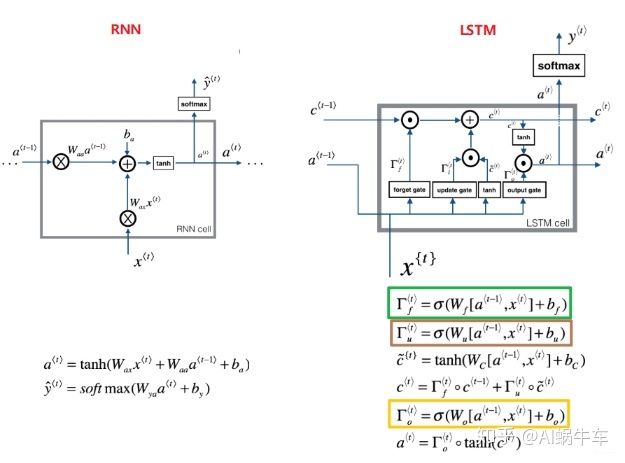
这就是LSTM的原理和计算细节了, 通过LSTM和RNN对比的方式再来总结一下LSTM:
看这个对比就能发现, LSTM比RNN更加复杂, RNN这个在前向传播的时候, 是记住了每个时刻的状态信息, 然后往后传,这种网络带来的结果就是易发生梯度消失,无法捕捉长期依赖, 因为传递的过程中有一些干扰信息, 导致后面时刻参数更新没法借鉴距离远的前面时刻的值。
而LSTM在记忆这方面更加的灵活, 长短期记忆嘛, 功能如其名,就是既可以长期记忆也可以短期记忆,它在RNN的基础上增加了自由的选择记忆功能, 也就是会有一个记忆cell, 这里面会只存储和当前时刻相关的一些重要信息, 毕竟每个时刻关注的上下文点可能不一样, 这个交给网络自己选择, 光有cell也不能起到好作用, 还得有两个门协助它完成选择和过滤的功能, 所以遗忘门帮助它衡量需要记住多少前面时刻的状态信息, 更新门帮助它衡量需要记住当前时刻的多少状态信息, 这俩一组合就是比较理想的记忆了。 但是即使是这样, LSTM依然不放心把这个记忆作为输出, 又加入了一个输出门, 来自由的选择我用多少记忆的信息作为最后的输出, 所以LSTM有了这三个门, 有了记忆cell, 使它变得更加的灵活, 既可以捕捉短期依赖, 也可以捕捉长期依赖, 并且也缓解了梯度消失(后面会分析)。
下面我们就来看看LSTM是怎么解决梯度消失的问题的。
4. LSTM是如何解决RNN存在的梯度消失问题的
在上一篇文章中, 我们详细分析了RNN为什么会存在梯度消失现象, 本质上就是因为反向传播的时候, 有
我们先来看看这个LSTM里面那个参数相当于RNN里面的这个
由LSTM的结构可知, 在每个迭代周期,
而如果根据反向传播把LSTM的梯度结构展开, 也会包含连乘项, 正是这里的
回忆一下上面LSTM中的
把上面的导数化简出来:
而加上连乘符号, 也就是个这样
下面就看看这两个的区别, RNN上一篇文章已经分析了, 这里的
如果换成LSTM的话, t=20的时候参数更新的公式中,后面那些就不一定都是0了, RNN的时候是0, 是因为越往前, 连乘越厉害, 导致了梯度消失, 前面时刻的信息对于t=20的时候不起作用。 而LSTM的话, 由于LSTM会自动控制
这里也更加看到了门函数的强大功能, 门函数赋予了网络决定梯度消失程度的能力, 以及能够在每一个时间步设置不同的值, 它们的值是当前的输入和隐藏状态的习得函数。 当然这里还有起作用的一个东西就是那一长串里面的加法运算, 这种加法运算不想乘法那么果断(一个0就整体0), 加性的单元更新状态使得导数表现得更加“良性”。
当然这里还有个细节就是LSTM的反向传播并不是只有C这一条路,其实在其他路上依然会有梯度消失或者梯度爆炸的现象发生, 但LSTM只要改善了一条路径上的梯度, 就拯救了总体的远距离的依赖捕捉。至于详细的反向传播算法推导, 下面的链接给出了一篇, 当然下面的numpy实现LSTM的前向传播和反向传播的过程也稍微涉及一点。
5. LSTM前向传播的numpy实现及keras中LSTM层简单介绍
这里分两块, 第一块是用numpy简单的实现一下LSTM的前向传播和反向传播, 这样可以更好的弄清楚上面公式中各个变量的维度变化和LSTM的底层计算原理。 第二块是keras的LSTM层, 会介绍实际中如何使用LSTM。
5.1 LSTM的前向传播的numpy实现
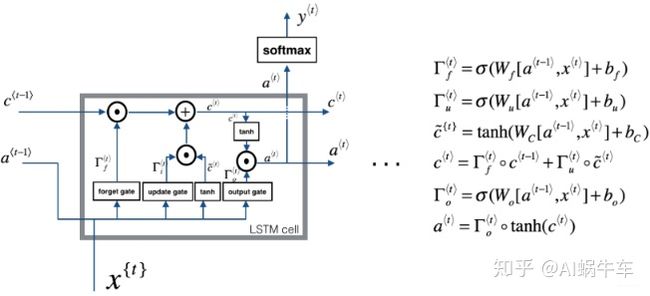
关于LSTM的前向传播,同样我们需要先从单个的单元进行分析
右边是前向传播的公式, 看左边的示意图我们发现, 该单元的输入是xt, a_prev, c_prev, 输出是ct, at, yt_pred。 依然假设每个时间步我们输入10个样本, input_dim是3, units是5, 那我们的输入(3, 10), a_prev是(5, 10), c_prev(5, 10)(这俩其实就和DNN那的输出一样, 输入是(3,10), units是5, 那么输入和第一层之间的W就是(5, 3), 那么WX之后的a就是(5,10)), 下面主要看看每个门中参数的维度:
- 输入门参数: Wf(units, units+input_dim), 这是因为上面先把a_prev和xt罗列了一下, (5, 10)和(3,10)第一维度拼接, 就是(8,10), 所以这里的Wf是(5, 8), 这样两者一乘才是(5,10)。 这里的bf是(5,1), 通过广播之后,得到的输出依然是(5,10)
- 更新门参数: 分析和上面同理, 所以Wi(5, 8), bi(5, 1)
- 输出门参数: Wo(5, 8), bo(5,1)
- C~t: Wc(5,8), bc(5,1)
- 而输出Wy, 这个的维度就是(n_y, units), by(n_y, 1), 因为这个和最终的输出有关了。
- 输出a_t: (5, 10), c_t(5, 10)
所以我们会发现这个Ct的维度是(5, 10), 也就是每个样本在每个神经元都有自己的记忆, 并且互不影响。 基于上面的分析, 就可以实现一步cell的前向传播了:
def lstm_cell_forward(xt, a_prev, c_prev, parametes):
# 得到参数
Wf = parameters["Wf"]
bf = parameters["bf"]
Wi = parameters["Wi"]
bi = parameters["bi"]
Wc = parameters["Wc"]
bc = parameters["bc"]
Wo = parameters["Wo"]
bo = parameters["bo"]
Wy = parameters["Wy"]
by = parameters["by"]
# 得到输入和输出维度
input_dim, m = xt.shape
n_y, units = Wy.shape
# 拼接a和x
concat = np.zeros([units+input_dim, m)
concat[:units, :] = a_prev
concat[units:, :] = xt
# 根据公式前向传播
ft = sigmoid(np.dot(Wf, concat) + bf)
it = sigmoid(np.dot(Wi, concat) + bi)
cct = np.tanh(np.dot(Wc, concat) + bc)
c_t = ft * c_prev + it * cct
ot = sigmoid(np.dot(Wo, concat) + bo)
a_t = ot * np.tanh(ct)
yt_pred = softmax(np.dot(Wy, a_t) + by)
# 存一下结果
cache = (a_t, c_t, a_prev, c_prev, ft, it, cct, ot, xt, parameters)
return a_t, c_t, yt_pred, cache
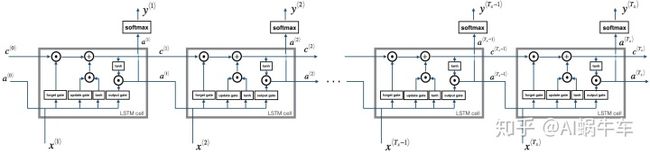
使用的时候, 按照维度初始化这些参数, 然后传入即可得到一个时间步的输出信息。 有了一个时间步的输出信息, 多个时间步无非就是一个循环:
这里参数的维度没有变化, 但是输入需要加上时间步的信息, 也就变成了3维, (input_dims, m, T_x)。 同理的这里的a, y, c也都变成了3维(units, m, T_x), (n_y, m, T_x), 因为每个时间步都会有a, y, c的输出
def lstm_forward(x, a0, parameters):
caches = []
# 获取输入和输出维度
input_dim, m, T_x = x.shape
n_y, units = parameters['Wy'].shape
# 初始化输入和输出
a = np.zeros((units, m, T_x))
c = np.zeros((units, m, T_x))
y = np.zeros((n_y, m, T_x))
# 初始化开始的a c
a_next = a0
c_next = np.zeros([units, m]) # 初始记忆为0
# 前向传播
for i in range(T_x):
a_next, c_next, yt, cache = lstm_cell_forward(x[:, :, t], a_next, c_next, parameters)
a[:, :, t] = a_next
c[:, :, t] = c_next
y[:, :, t] = yt
caches.append(cache)
caches = (caches, x)
return a, y, c, caches
至于LSTM的反向传播底层, 这里也不多说了,这个比较复杂, 大部分时间都是在求导, 而实际使用的时候, 比如keras,Pytorch, tf等其实都把反向传播给实现了, 我们并不需要自己去写。 所以我们重点需要知道的是在实际中LSTM到底应该怎么用。
下面就拿最简单实用的keras的LSTM举例。
5.2 Keras的LSTM
keras里面搭建一个LSTM网络非常简单, LSTM层的表示如下:
keras.layers.recurrent.LSTM(units, activation='tanh', recurrent_activation='hard_sigmoid', use_bias=True, kernel_initializer='glorot_uniform', recurrent_initializer='orthogonal', bias_initializer='zeros', unit_forget_bias=True, kernel_regularizer=None, recurrent_regularizer=None, bias_regularizer=None, activity_regularizer=None, kernel_constraint=None, recurrent_constraint=None, bias_constraint=None, dropout=0.0, recurrent_dropout=0.0)
这里面有几个核心的参数需要说一下, 其实RNN那个地方也作了铺垫:
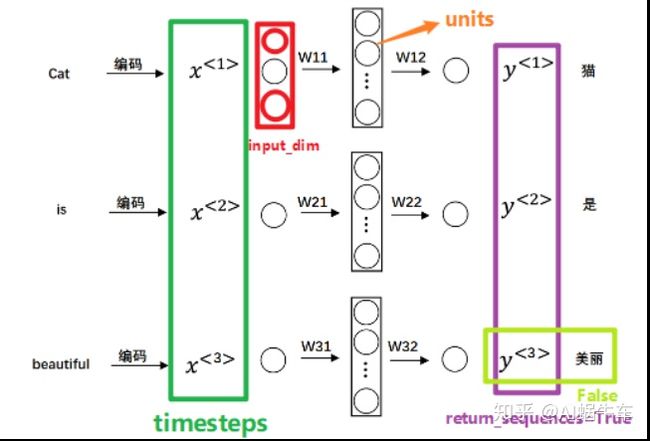
- units: 这个指的就是隐藏层神经元的个数, 也是该层的输出维度
- input_dim: 这个是输入数据的特征数量, 当该层作为模型首层时, 就需要指定这个
- return_sequences:布尔值,默认False,控制返回类型。若为True则返回整个序列,否则仅返回输出序列的最后一个输出, 这个也就是说如果是True, 就返回每个时间步的输出, 而False,只返回最后一个时间步的输出。 这个参数来自于LSTM的父类, 这里的输出指的是hidden state里面的值, 也就是上面符号里面的h或者a。
- return_state: 默认为False, 表示是否返回输出之外的最后一个状态, 这个和return_sequences不一样, 最后一个状态, 其实是包含两个值的, 一个是hidden state的值, 一个是cell state的值,也就是h和c。
- return_sequences的True表示返回所有时间步中的h, False表示返回最后一个时间步的h
- return_state的True表示返回最后一个时间步的h和c, False表示不返回。 详细的看下面的keras中的LSTM内部机制代码理解的链接
- timesteps: 这个就是时间序列的长度或者说时间步有多少个。 比如I love China。 时间序列的长度为3, 所以这里的timesteps就是3.
- input_length: 这个其实对应timesteps, 表示输入序列的长度。 当需要在该层后连接Flatten层,然后又要连接Dense层时,需要指定该参数,否则全连接的输出无法计算出来。
LSTM层接收的输入, 是(samples, timesteps, input_dim)的3D张量, 输出的维度, 如果return_sequences=True, 那么就返回(samples, timesteps, units)的3D张量, 否则就是(samples, units)的2D张量。 这个还是举个例子吧: 比如我们输入100个句子, 每个句子有5个单词, 而每个参数是64维词向量embedding了。 那么samples=100, timesteps=5, input_dim=64。
所以, 只要根据规定的输入去构造自己的数据, 然后就可以进行神经网络的搭建, 下面也给出一个小demo:
X = Input(shape=[trainx.shape[1], trainx.shape[2], ])
h = LSTM(
units=10,
activation='relu',
kernel_initializer='random_uniform',
bias_initializer='zeros'
)(X)
Y = Dense(1)(h)
model = Model(X, Y)
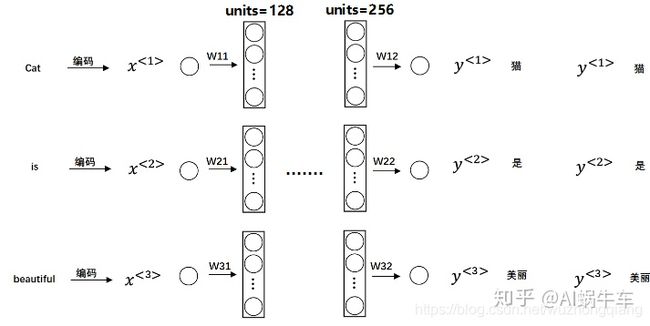
上面这个是最简单的一层LSTM网络, 当然也可以搭多层, 多层的话一般前面的层return_sequences为True, 最后一层return_sequences为false。
model = Sequential()
model.add(LSTM(128, input_dim=64, input_length=5, return_sequences=True))
model.add(LSTM(256, return_sequences=False))
就是一个这样的感觉,
6. LSTM的变体GRU
GRU是LSTM网络的一种效果很好的变体,2014年提出, 它较LSTM网络的结构更加简单,而且效果也很好,因此也是当前非常流形的一种网络。GRU既然是LSTM的变体,因此也是可以解决RNN网络中的长依赖问题。
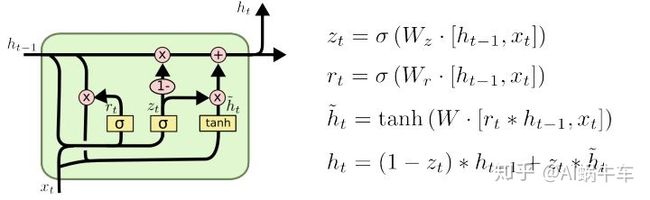
首先是看一下GRU内部的一个计算逻辑:
与上面的LSTM相比, 我们会发现这里成了两个门, 一个是
另一个改变是这里的hidden state和cell state进行了合并, 两者保持了一致, 成了一个输出, 而LSTM那里这俩是不一样的。下面就看看这些公式到底在干啥:
前两个公式是两个门的计算公式, sigmoid函数, 把这两个门的输出控制到了0-1, 看上面
关于GRU的太多细节, 这里就不多说了,很多都是和LSTM类似,毕竟是基于LSTM改变的一个变体, 与LSTM相比,GRU的优势就是内部少了一个”门控“,参数比LSTM少,因而训练稍快或需要更少的数据来泛化, 达到的效果往往能和LSTM差不多, 但是GRU不如LSTM灵活, 如果有足够的数据, LSTM的强大表达能力可能会产生更好的效果。 至于使用, keras里面也有GRU层可以帮助我们搭建GRU网络。 核心参数和LSTM的基本一样, 可以参考LSTM那里。
7. 总结
这篇文章, 把RNN的两个常用变体LSTM和GRU整理了一遍, 重点放在了LSTM上, 因为GRU可以看成一个LSTM的简化版本,是在LSTM上的改进,有很多思想借鉴了LSTM, 所以LSTM的原理和细节作为了重点整理。 下面简单梳理:
首先, 从RNN的梯度消失和不能捕捉长期依赖开始引出了LSTM, 这个结构就是为了解决RNN的这两个不足, 然后介绍了RNN的内部细节及计算逻辑, LSTM的关键就是引入了可选择性的记忆单元和三个门控, 使得它变得更加灵活,可以自由的管理自己的记忆, 每一步的隐态更新都会衡量过去的信息与当前信息, 通过门控机制更合理的去更新记忆,然后去更新隐藏状态。 有了门控, 有了加性机制,也帮助了LSTM减缓梯度消失, 使得反向传播过程中的连乘现象变得自己可控, 当前时刻的某些参数更新取决于过去哪些时刻让LSTM自己来选择。 最后通过numpy实现了一下LSTM的前向传播过程更好的帮助我们去了解细节,比如各个变量的维度信息。
最后简单介绍了LSTM的一个变体叫做GRU, GRU在LSTM的基础上把遗忘门和输入门进行了合并, 改成了一个更新门, 依赖这一个门就可以自由的选择当前时刻的信息取决于多少过去,多少当前。 然后还加入了一个重置门, 来控制当前时刻的信息更新有多少依赖于前一时刻的隐态, 增加了一定的灵活性, 并且还把cell 和hidden合并成了一个输出。 这个结构使得网络更加容易训练, 参数较少, 但是表达能力不如LSTM强。
参考:
- 深入理解lstm及其变种gru
- 人人都能看懂的LSTM
- 理解LSTM(通俗易懂版)
- 为什么LSTM可以阻止梯度消失:从反向传播视角来考虑(博客翻译)
- Why LSTMs Stop Your Gradients From Vanishing: A View from the Backwards Pass
- LSTM如何解决梯度消失问题
- LSTM如何解决梯度消失问题
- 图解LSTM与GRU单元的各个公式和区别
- 人人都能看懂的LSTM介绍及反向传播算法推导(非常详细)
- keras:4)LSTM函数详解
- keras中的LSTM内部机制代码理解
- 难以置信!LSTM和GRU的解析从未如此清晰(动图+视频)
- 从动图中理解 RNN,LSTM 和 GRU
- 人人都能看懂的GRU