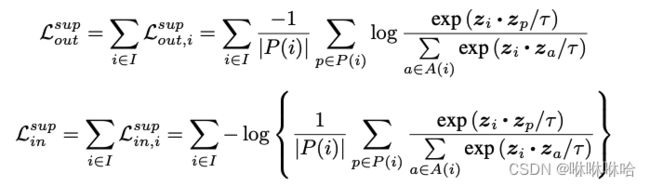对比学习系列论文

Supervised Contrastive Learning论文梳理

最近在看分类的相关论文，有很多不错的算法，其中一个分支是基于对比学习的。上次小组周会，小师妹分享了Supervised Contrastive Learning这篇论文，是Google Research 2021年发表在MachineLearning上，将对比学习思想推广到完全监督学习的范式中，更加充分地利用标签信息。目前这篇论文的引用量是800+。小师妹讲的非常完整，由浅入深，结合小师妹讲的，我做了进一步整理，顺便也理了理对比学习的一些发展。
欢迎阅读小师妹的早期作品，介个是她的个人主页https://blog.csdn.net/qq_42311648

1、什么是对比学习，它为什么work呢？

说起分类，大家自然而然就会想，分类是基于某些相似的特征进行分类的，比如猫狗分类，狗和猫的耳朵，尾巴等形态特征存在着一些差异，神经网络在区分两者的时候，要找到狗狗们共有的且区别于猫咪的特征，

我们知道，神经网络作为特征提取器会学习到每张图片对应的特征表示，通常最终得到的是一个多维向量，比如512x1维的一个向量(即最后送入分类器的特征)来表示这张图片。这一过程就是将原数据映射到了抽象语义级别的高维特征空间，学习原始数据在抽象语义空间的特征表示。

近几年对比式学习用在无监督领域大火，如下图(b)所示，在CPC，MoCo等基于对比学习的无监督工作中，在Stage 1，同一张图像通过随机数据扩充得到的两张图像构成一对样本，模型学习的目标是拉近成对样本的距离，拉大非成对样本的距离，以此获得每张图片的特征表示，然后在stage 2通过分类器对这些特征进行分类。

那这种情况下自然也就存在一个弊端，对于不是来自于同一张图像的同类样本，距离也可能被拉远。

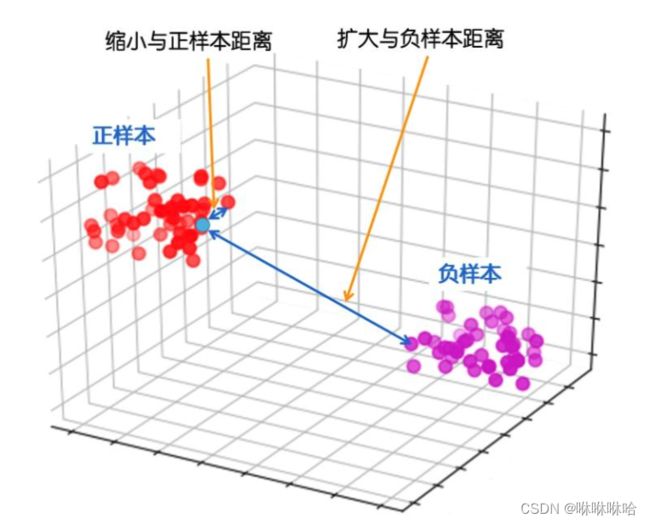
而将对比学习引入监督学习后，则可以解决这一问题。如上图©所示，和无监督对比学习相同的是仍旧分为两个stages进行学习，不同的是成对样本的构建方式——只要图像拥有同类标签，就是成对样本。模型学习的目标变成了拉进同类样本的距离，拉远不同类样本的距离，这使得模型学习到的特征更具有类别可区分性。可以把这个过程想象成聚类，将同一类的特征表示拉近成一簇，不同类的距离尽可能远。

(关于在监督学习和自监督学习中的区别，第4节会展开来将)

从编码器的角度来说，对比学习的目标是学习一个编码器，此编码器对同类数据进行相似的编码，并使不同类的数据的编码结果尽可能的不同。

2、Triplet Loss–对比单个正样本和单个负样本

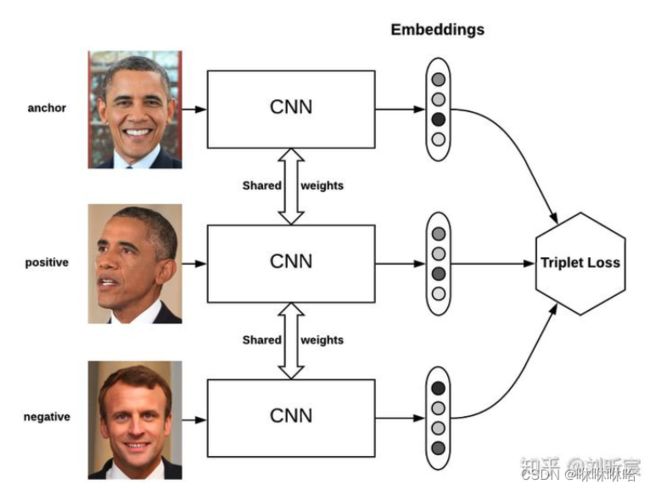
2015年Google发表在CVPR上的这篇论文——《FaceNet: A Unified Embedding for Face Recognition and Clustering》提出了triplet loss：
$$L=\max \{d(x,x^{+})-d(x,x^{-})+margin,0\}$$
通过triplet loss来对比由$(anchor:x,positive:x^{+},negative:x^{-})$组成的triplet，从而拉近正样本$x^{+}$和anchor的距离，拉远负样本$x^{-}$和anchor的距离。

使得模型最终学到的特征对于任何样本$x$基本都能达到如下所示的状态：
$$d(x,x^{-})>d(x,x^{+})+margin$$
margin在这里发挥的作用：

1、避免模型走捷径，margin会迫使模型让anchor和负样本之间的距离更大，让anchor和负样本之间的距离更小，使得模型学习到的正负样本表征之间的差异更大。

如果margin=0，triplet loss就变成了$L=\max \{d(x,x^{+})-d(x,x^{-}),0\}$，那么当正样本和负样本到anchor的距离相等时，也会出现损失为0的情况，这样模型便很难区分正负样本了。

2、对于相似样本(semi-hard triplets, hard triplets)有更好的推开作用。

（这里是直接用的引用博客里的图片，如果不合适，请读者指出正确的引用图片方式哈，感谢了）

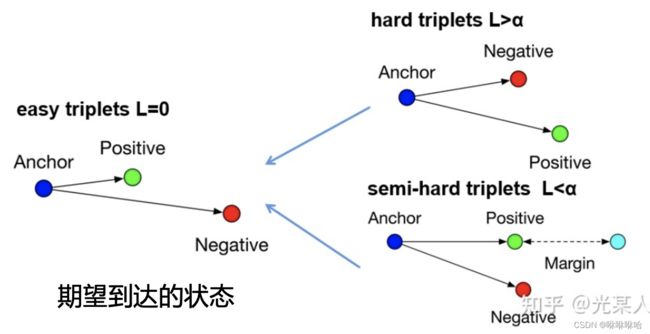
• easy triplets: 此时loss为 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-c6GmuS7p-1654435367008)(https://www.zhihu.com/equation?tex=0)] ，这种情况是我们最希望看到的，可以理解成是容易分辨的triplets。即 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-l4uNEIs7-1654435367009)(https://www.zhihu.com/equation?tex=d%28a%2Cp%29%2Bmargin+%3C+d%28a%2Cn%29)]
• hard triplets: 此时negative比positive更接近anchor，这种情况是我们最不希望看到的，可以理解成是处在模糊区域的triplets。即 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cCwF3cAD-1654435367009)(https://www.zhihu.com/equation?tex=d%28a%2Cn%29+%3C+d%28a%2Cp%29)]
• semi-hard triplets: 此时negative比positive距离anchor更远，但是距离差没有达到一个margin，可以理解成是一定会被误识别的triplets。

比如下图的semi-hard triplets，由于margin的存在，损失会引导模型进一步拉近正样本和anchor的距离，拉远负样本和anchor的距离，也就是放大相似样本的差异，最终达到期望的状态。

当然triplet loss也存在一些不足，由于每个triplet只包含一个负样本，在计算loss时，只拿一个负样本和当前的正样本比较距离，没有考虑其他负样本的情况，这就导致了在随机产生的数据对中，每一个数据对并不能有效的保证当前优化的方向能够拉远所有负类样本的距离，这就导致了往往训练过程中的收敛不稳定或者陷入局部最优。

3、N-pair Loss–对比单个正样本和所有负样本

N-pair loss 的提出就是解决这个问题的，出发点就是同时优化使用的所有负类。

$f_i,f_j$表示两个向量之间的相似性（余弦相似性）。

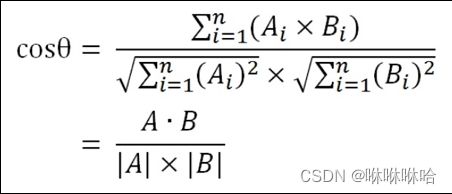
这里用余弦相似性来度量两个向量的相似性，在triplet loss里面使用欧式距离度量向量之间的相似性，下文大家还会看到用向量的内积(inner product)来度量样本相似性，大家可以根据不同的场景选择合适的相似的度量方式。

4、从自监督对比学习到监督对比学习

在自监督学习中，对比学习的损失函数可以概括为以下形式：

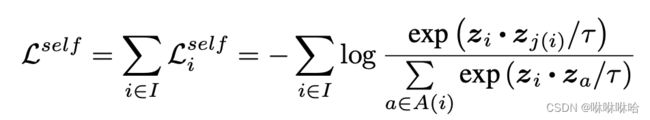
在自监督学习中，数据是没有标签的，所以通常需要对样本$i$构建一个样本对$[i,i^{+}]$，$i,i^{+}$都来自同一张图片，互为正样本。

对于一个batch(batch_size=N)，通过数据扩增得到两个batch的数据，从两个batch中任意选取一个样本 $i$ 作为anchor, $i\in I=\{1....2N\}$，$i^{+}$ 是 $i$ 对应的正样本，剩下$2N-2$个样本对$i$来说是负样本，集合$A(i)$包含除了样本$i$之外的所有样本。$z_i$表示样本$i$通过卷积神经网络的到的表征向量，$\tau$是温度系数，这里用内积表示 $z_i,z_k(k\ne i,k\in A(i))$ 之间的相似性。在下面的分析中，我们用 $s_{i,k}$ 来表示$z_i,z_k$的相似性。

直观来说，该损失函数要求第i个样本和正样本j(i)之间的相似度 尽可能大，而与其他2N-2的负样本之间的相似度尽可能小。

接下来我们从梯度层面分析一下这个函数的优点：

对样本$x_i$来说，$L(x_i)$对正样本梯度和负样本梯度分别为：
$$\frac{\partial L(x_i)}{\partial s_{i,i^{+}}}=-\frac{1}{\tau }\sum _{k\ne i^{+}}{P}_{i,k}$$
对负样本梯度分别为：
$$\frac{\partial L(x_i)}{\partial s_{i,j}}=\frac{1}{\tau }{P}_{i,j},(j\ne i^{+},j\in A(i))$$

其中：
$$P_{i,j}=\frac{exp(s_{i,j}/\tau )}{{\sum }_{k\ne i^{+}}exp(s_{i,k}/\tau )+exp(s_{i,i^{+}}/\tau )}$$

公式推导：

$$\begin{array}{rl}\frac{\partial L(x_i)}{\partial s_{i,i^{+}}}& =\frac{\partial [-\log \frac{f(x)}{A+f(x)}]}{\partial x},其中x=s_{i,i^{+}},A=\sum _{k\ne i^{+}}exp(s_{i,k}/\tau )，f(x)=exp(s_{i,i^{+}}/\tau )\\ & =\frac{\partial \{-\log f(x)+log(A+f(x))\}}{\partial x}\\ & =-\frac{f^{\prime }(x)}{f(x)}+\frac{f^{\prime }(x)}{A+f(x)}\\ & =-\frac{1}{\tau }+\frac{1}{\tau }\frac{exp(s_{i,i^{+}}/\tau )}{{\sum }_{k\ne i^{+}}exp(s_{i,k}/\tau )+exp(s_{i,i^{+}}/\tau )}\\ & =-\frac{1}{\tau }\frac{{\sum }_{k\ne i^{+}}exp(s_{i,k}/\tau )}{{\sum }_{k\ne i^{+}}exp(s_{i,k}/\tau )+exp(s_{i,i^{+}}/\tau )}\end{array}$$

$$\begin{gathered} 令P_{i,j}=\frac{exp(s_{i,j}/\tau )}{{\sum }_{k\ne i^{+}}exp(s_{i,k}/\tau )+exp(s_{i,i^{+}}/\tau )},则有\frac{\partial L(x_i)}{\partial s_{i,i^{+}}}=-\frac{1}{\tau }\sum _{k\ne i^{+}}{P}_{i,k} \\ 类似的有\frac{\partial L(x_i)}{\partial s_{i,j}}=\frac{1}{\tau }{P}_{i,j}(j\in A(i),j\ne i^{+}) \end{gathered}$$

到这里公式推导就结束了。下面我们来看一下基于以上推导的正负样本的梯度，分析一下infoNCE有什么特性。

对于所有的负样本比较来说，$P_{i,j}$ 的分母项都是相同的。那么$s_{i,j}$越大，则$P_{i,j}$的分子项越大，梯度也越大。也就是说对比损失给予了更相似（困难）的负样本更大的远离该样本的梯度。其中 $\tau$ 是温度系数，可以控制对困难样本的关注程度。

对比正负样本的梯度，我们可以发现，损失对正样本的梯度绝对值等于所有对负样本的梯度值绝对值的和，即：
$$\frac{|{\sum }_{k\ne i^{+}}\frac{\partial L(x_i)}{\partial s_{i,k}}|}{|\frac{\partial L(x_i)}{\partial s_{i,i^{+}}}|}=1$$
所以，对于每个负样本 $j$ 的惩罚权重为：
$$r_i(s_{i,j})=|\frac{\partial L(x_i)}{\partial s_{i,j}}|/|\frac{\partial L(x_i)}{\partial s_{i,j(i)}}|=\frac{exp(s_{i,j}/\tau )}{{\sum }_{k\ne i^{+}}exp(s_{i,k}/\tau )+exp(s_{i,i^{+}}/\tau )}$$
至此，我们会看到这不就是softmax函数嘛！顺便复习一下softmax函数中温度系数的影响。当温度系数很小时，例如下图蓝色曲线$\tau =0.07$，$s_{i,j}$的增大会使得惩罚梯度剧烈的增大，也就是会给予相似度大的负样本更多的关注。而当温度系数逐渐增大，相对梯度的熵逐渐也增大，概率分布逐渐接近均匀分布，例如图中的绿色线，那么对相似度大的负样本的关注度逐渐减小。

看懂了自监督对比损失，《Supervised Contrastive Learning》这篇论文里提出的监督对比损失就好理解很多了。

论文的引言部分放出了下图，非常形象地解释了有监督对比损失和自监督对比损失的区别。

对于自监督对比损失，即便同一个batch中包含和anchor同类的样本，也会被认定为anchor的负样本，从而被拉远。但在监督对比学习中，只要和anchor相同的类，也就是在同一个batch中，并且具有相同的类别标签，就会拉近。

论文里给出了两种监督对比损失：

$P(i)$在这里指的就是同一个batch中和样本$i$ 具有相同类别标签的所有样本的集合。

这两个Loss都有三个特性：

•接受任意数量的正样本数；

•负样本越多，对比能力越强：保留了负样本的累加；

•艰难样本挖掘。

但是这两个式子并不等价。对于$L_{out}$，$1/|P(i)|$ 用于消除多视图batch中多个正阳本导致的偏置。简单来说对多个正样本的损失求平均，一定程度上消除了某些偏置较大的正样本带来的影响。

然而，尽管$L_{in}$也包含相同的因子，但它位于log中，相当于$log\sum -log(p(i))$(简写一下，请意会)。因此，它只对总损失贡献一个附加常数，而不影响梯度，没有任何归一化效应。

论文中也基于ImageNet的分类任务给出了实验结果证明了$L_{out}$要更优于$L_{in}$，还配了详细的理论推导分析，这里就不再展开说了。

最后说一下温度系数 $\tau$ 的影响：

• 光滑性: $|\nabla L|\propto \frac{1}{\tau }$，梯度和$\tau$ 成反比。取较大的$\tau$，会得到较小的梯度，同时也允许较大的学习速率，从而使优化问题更简单。在单个正负样本的情况下，$\tau$相当于triplet loss中的margin，较大的温度会使类更容易被分开。

• 艰难样本挖掘: 与infoNCE结构类似，具有困难样本挖掘的能力，对于一个batch的样本和一个特定的anchor，较低的$\tau$ ，对于大内积的样本，$P_{i,j}$ 增大，梯度增大；对于具有小内积的样本，$P_{i,j}$ 减小，梯度减小。

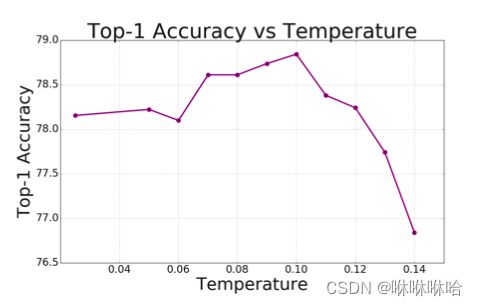
  论文里给出了基于ImageNet分类任务，使用 ResNet-50作为编码器的试验结果，$\tau =0.1$ 时效果最好

  

  作者也说道： 较小的温度比较高的温度更有利于区分难例，但由于数值不稳定，极低的温度更难训练，对学习率等参数的设置也更敏感。所以针对具体的数据集和问题，还需要我们根据实验结果去合适的 $\tau$ 。

我在实验过程中，也在思考batch size的影响，是不是batch size越大越好呢？

作者在论文中也放出了实验结果。可以看到随着batch size的增大，Top-1 Accuracy也在增加，但增速越来越缓慢。

Top-1 Accuracy的增长是由于在每次对比学习时，标准的正样本增加了，负样本也增加了，每次对比学习学到的东西也更加有区分性。

此外，作者在论文4.5Training Details中还提到了对于固定的批大小，使用SupCon进行训练，使用比交叉熵损失所需的更大的学习率，可以获得类似的性能。

参考链接

本文的一些图片和理解主要源于下面的博文

对比学习综述：https://zhuanlan.zhihu.com/p/346686467

triplet loss：https://zhuanlan.zhihu.com/p/295512971