PyTorch学习笔记1——基本概念、模块简介、张量操作、自动微分
文章目录
-
- 一、基础介绍
-
- 1.1PyTorch 简介:
- 1.2 静态图和动态图
- 1.3 pytorch主要模块
- 二、 张量
-
- 2.1.张量的创建方式
- 2.2 张量类型和维度
- 2.3 张量的存储设备
- 2. 4 索引和切片
- 2.5 函数运算、排序sort、范数
-
- 2.5.1 函数运算
- 2.5.2 范数
- 2.6 向量点积、乘积和张量的缩并einsum
-
- 2.6.1 向量点积(DotProduct、点乘、内积、数量积)
- 2.6.2 矩阵-向量积
- 2.6.3 矩阵-矩阵乘法
- 2.6.4 向量的普通乘积
- 2.6.5 矩阵的Hadamard积
- 2.6.4 向量的外积
- 2.7 张量的拼接和分割split
- 2.8 张量扩增(unsqueeze)、压缩(squeeze)和广播
- 2.9 原地操作
- 三. PyTorch 自动微分
-
- 3.1 autograd 自动求导和冻结参数
- 3.2 雅克比向量积
- 3.3 计算图
推荐文章《PyTorch 学习笔记汇总(完结撒花)》
一、基础介绍
1.1PyTorch 简介:
- Torch是一个有大量机器学习算法支持的科学计算框架,是一个与Numpy类似的张量(Tensor) 操作库,其特点是特别灵活,但因其采用了小众的编程语言是Lua,所以流行度不高。
- PyTorch是一个基于Torch的Python开源机器学习库,提供了两个高级功能:
- 具有强大的GPU加速的张量计算(如Numpy)
- 包含自动求导系统的深度神经网络
- PyTorch,通过反向求导技术,可以让你零延迟地任意改变神经网络的行为,而且其实现速度快
- 底层代码易于理解 +命令式体验 +自定义扩展
- 缺点,PyTorch也不例外,对比TensorFlow,其全面性处于劣势。例如目前PyTorch还不支持快速傅里 叶、沿维翻转张量和检查无穷与非数值张量等
1.2 静态图和动态图
为了能够计算权重梯度和数据梯度,神经网络需记录运算的过程,并构建出计算图。
- 静态图:tensorflow和caffe。先构建模型对应的静态图,再输入张量。执行引擎会根据输入的张量进行计算,最后输出深度学习模型的计算结果。
- 静态图的前向和反向传播路径在计算前已经被构建,所以是已知的。计算图在实际发生计算之前已经存在
- 执行引擎可以在计算之前对计算图进行优化,比如删除冗余的运算合并两个运算操作等
- 执行效率较高:不用每次计算都重新构建计算图,减少了计算图构建的时间消耗
- 不够灵活:因为静态计算图在构建完成之后不能修改,使用条件控制(比如循环和判断语句)会不大方便
- 代码调试较慢:构建时只能检查静态参数,如输入输出形状。执行时的问题无法在构件图时预先排查
- 计算图中直接集成了优化器,求出权重张量梯度,直接执行优化器的计算图,更新权重的张量值
- 动态图:在计算过程中逐步构建计算图。牺牲执行效率但是更灵活
- 反向传播路径只有在构建完计算图时才能获得
- 条件控制语句很简单
- 调试方便:可以实时输出模型的中间张量
- 优化器绑定在权重张量上:反向传播后,优化器根据绑定的梯度长量更新权重张量。
- 强大的可扩展性。例如自由定制张量计算、CPU/GPU异构计算、并行计算环境、设置不同模型层的学习率等。
1.3 pytorch主要模块
下面介绍主要模块。具体都可以参考官方文档。
- torch模块:包含激活函数和主要的张量操作
- torch.Tensor模块:定义了张量的数据类型(整型、浮点型等)另外张量的某个类方法会返回新的张量,如果方法后缀带下划线,就会修改张量本身。比如Tensor.add是当前张量和别的张量做加法,返回新的张量。如果是ensor.add_就是将加和的张量结果赋值给当前张量。
- torch.cuda:定义了CUDA运算相关的函数。如检查CUDA是否可用及序号,清除其缓存、设置GPU计算流stream等
- torch.nn:神经网络模块化的核心,包括卷积神经网络nn.ConvNd和全连接层(线性层)nn.Linear等,以及一系列的损失函数。
- torch,nn.functional:定义神经网络相关的函数,例如卷积函数、池化函数、log_softmax函数等部分激活函数。torch.nn模块一般会调用torch.nn.functional的函数。
- torch.nn.init:权重初始化模块。包括均匀初始化torch.nn.init.uniform_和正态分布归一化torch.nn.init.normal_。(_表示直接修改原张量的数值并返回)
- torch.optim:定义一系列优化器,如optim.SGD、optim.Adam、optim.AdamW等。以及学习率调度器torch.optim.lr_scheduler。并可以实现多种学习率衰减方法等。具体参考官方教程。
- torch.autograd:自动微分算法模块。定义一系列自动微分函数,例如torch.autograd.backward反向传播函数和torch.autograd.grad求导函数(一个标量张量对另一个张量求导)。以及设置不求导部分。
- torch.distributed:分布式计算模块。设定并行运算环境
- torch.distributions:强化学习等需要的策略梯度法(概率采样计算图) 无法直接对离散采样结果求导,这个模块可以解决这个问题
- torch.hub:提供一系列预训练模型给用户使用。torch.hub.list获取模型的checkpoint,torch.hub.load来加载对应模型。
- torch.random:保存和设置随机数生成器。manual_seed设置随机数种子,initial_seed设置程序初始化种子。set_rng_state设置当前随机数生成器状态,get_rng_state获取前随机数生成器状态。设置统一的随机数种子,可以测试不同神经网络的表现,方便进行调试。
- torch.jit:动态图转静态图,保存后被其他前端支持(C++等)。关联的还有torch.onnx(深度学习模型描述文件,用于和其它深度学习框架进行模型交换)
除此之外还有一些辅助模块:
- torch.utils.benchmark:记录深度学习模型中各模块运行时间,通过优化运行时间,来优化模型性能
- torch.utils.checkpoint:以计算时间换空间,优化模型性能。因为反向传播时,需要保存中间数据,大大增加内存消耗。此模块可以记录中间数据计算过程,然后丢弃中间数据,用的时候再重新计算。这样可以提高batch_size,使模型性能和优化更稳定。
- torch.utils.data:主要是Dataset和DataLoader。
- torch.utils.tensorboard:pytorch对tensorboard的数据可视化支持工具。显示模型训练过程中的
损失函数和张量权重的直方图,以及中间输出的文本、视频等。方便调试程序。
二、 张量
pytorch提供专门的torch.Tensor类,根据张量的数据格式和存储设备(CPU/GPU)来存储张量。
Tensors 类似于 NumPy 的 ndarrays ,同时 Tensors 可以使用 GPU 进行计算。
详细的张量操作参考:torch.Tensor、张量创建和运算: torch
2.1.张量的创建方式
- python列表、ndarray数组转为张量
torch.tensor([[1., -1.], [1., -1.]])#python列表转为张量,子列表长度必须一致
torch.tensor(np.array([[1, 2, 3], [4, 5, 6]]))#ndarray数组转为张量
x_np = torch.from_numpy(np_array)
张量转为numpy数组,大小为1的张量可以转为python标量:
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
A = X.numpy()
B = torch.tensor(A)
a = torch.tensor([3.5])
a, a.item(), float(a), int(a)
- 利用函数创建张量
shape = (2,3,)
rand_tensor = torch.rand(shape)
ones_tensor = torch.ones(shape)
zeros_tensor = torch.zeros(shape)
- 常见的构造Tensor的函数:
| 函数 | 功能 |
|---|---|
| ensor(sizes) | 基础构造函数 |
| tensor(data) | 类似于np.array |
| ones(sizes) | 全1 |
| zeros(sizes) | 全0 |
| eye(sizes) | 对角为1,其余为0 |
| arange(s,e,step) | 从s到e,步长为step |
| linspace(s,e,steps) | 从s到e,均匀分成step份 |
| randn(sizes) | 标准正态分布 |
| rand(size) | [0,1)j均匀分布 |
| normal(mean,std) | 正态分布 |
| uniform(from,to) | 均匀分布 |
| randint(a,b,(sizes)) | 从a到b形状为size的整数张量 |
| randperm(m) | 随机排列 |
- 创建类似形状的张量:
t=torch.randn(3,3)
torch.zeros_like(t)#zeros还可以换成其它构造函数ones、randdeng
#如果t是整型,构造函数生成浮点型会报错
2.2 张量类型和维度
- 访问dtype属性可以查看张量的类型。shape属性可以查看张量的形状
a=torch.tensor([[1., -1.], [1., -1.]])
print(a.dtype,a.type(),a.shape)
torch.float32 torch.FloatTensor torch.Size([2, 2])
- pytorch不同数据类型之间可以用to转换,或者.int()方法
#浮点型转整型
torch.randn(3,3).to(torch.int)
torch.randn(3,3).int()
- 张量的维度
t=torch.randn(3,4).to(torch.int)
t.nelement()#获取元素总数
t.ndimension()#获取张量维度
t.shape#张量形状
- 改变张量的维度可以用view方法,指定n-1维,最后一维写-1
t.view(4,3)
t.view(-1,3)
t.view(12)#tensor([0, 0, 0, 0, -1, 1, 0, 2, 0, 2, 0, 0], dtype=torch.int32)
另外还有reshape和contiguous方法。reshape和view区别在于被操作的那个tensor是否是连续的:
- 当连续时两者一致,当不连续时reshape会返回新的tensor,该tensor与原来的再无关联
- view只能作用在连续的张量上(张量中元素的内存地址是连续的)。而reshape连续or非连续都可以。调用x.reshape的时候,如果x在内存中是连续的,那么x.reshape会返回一个view(原地修改,此时内存地址不变),否则就会返回一个新的张量(这时候内存地址变了)。
- 推荐的做法是,想要原地修改就直接view,否则就先clone()再改。
2.3 张量的存储设备
两个张量只有在同一设备上才可以运算(CPU或者同一个GPU)
nvidia-smi#可以查看GPU的信息
!nvidia-smi#colab上命令是这个
torch.randn(3,3,device='cuda:0').device#在0号cuda上创建张量,查看张量存储设备
device(type='cuda', index=0)
torch.randn(3,3,device='cuda:0').cpu().device#cuda 0上的张量复制到CPU上
device(type='cpu')
torch.randn(3,3,device='cuda:0').cuda(1)
torch.randn(3,3,device='cuda:0').to('cuda:1')
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 495.44 Driver Version: 460.32.03 CUDA Version: 11.2 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|===============================+======================+======================|
| 0 Tesla P100-PCIE... Off | 00000000:00:04.0 Off | 0 |
| N/A 47C P0 28W / 250W | 0MiB / 16280MiB | 0% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: |
| GPU GI CI PID Type Process name GPU Memory |
| ID ID Usage |
|=============================================================================|
| No running processes found |
+-----------------------------------------------------------------------------+
2. 4 索引和切片
等同numpy的操作。如:
t=torch.randn(3,4,5)
t[:,1:-1,1:3])
t>0#得到一个掩码矩阵
t[t>0]
筛选出t中大于0的元素,最终得到一个一维向量
如果不想改变原张量的数值,可以先用clone得到张量的副本,再进行索引和切片的赋值操作。
2.5 函数运算、排序sort、范数
2.5.1 函数运算
所有运算符、操作符见文档:《Creation Ops》
t.mean()#对所有维度求均值
t.mean(0)#对第0维元素求均值
t.mean([0,1])#对0,1两维元素求均值
- argmax和argmin可以根据传入的维度,求的该维度极大极小值对应的序号。
- max和min会得到一个元组,包括极值位置和极值。
- sort默认从小到大排序。从大到小需要设置descending=True。需要传入排序的维度,返回排序后的张量和各元素在原始张量的位置
- sum可以按指定轴求和(求和后降低维度),keepdims=True可以保持非降维求和,以便后续广播计算。
- cumsum函数:计算沿指定轴的累加和
t=torch.randint(1,100,(3,4))
tensor([[20, 95, 9, 94],
[97, 61, 80, 67],
[76, 66, 64, 65]])
t.max(0),t.argmax(0),t.sort(-1,descending=True)
torch.return_types.max(values=tensor([97, 95, 80, 94]),indices=tensor([1, 0, 1, 0]))
tensor([1, 0, 1, 0])
torch.return_types.sort(values=tensor([[95, 94, 20, 9],
[97, 80, 67, 61],
[76, 66, 65, 64]]),
indices=tensor([[1, 3, 0, 2],
[0, 2, 3, 1],
[0, 1, 3, 2]]))
s=t.sum(0,keepdims=True)#结果还是一个二维矩阵
a=t/s
print(s,a)
(tensor([[193., 222., 153., 226.]])
tensor([[0.1036, 0.4279, 0.0588, 0.4159],
[0.5026, 0.2748, 0.5229, 0.2965],
[0.3938, 0.2973, 0.4183, 0.2876]]))
a=torch.arange(20).reshape(4,5)
a,a.cumsum(0)#沿每一列做累加和
tensor([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
tensor([[ 0, 1, 2, 3, 4],
[ 5, 7, 9, 11, 13],
[15, 18, 21, 24, 27],
[30, 34, 38, 42, 46]])
函数后面加下划线是原地操作,改变被调用的张量的值
2.5.2 范数
在线性代数中,向量范数是将向量映射到标量的函数f。⾮正式地说,⼀个向量的范数告诉我们⼀个向量有多⼤。这⾥考虑的⼤⼩(size)概念不涉及维度,⽽是分量的⼤⼩。
- L1范数是向量元素的绝对值之和:(
∥ x ∥ 1 = ∑ i = 1 n ∣ x i ∣ \left \| x \right \|_{1}=\sum_{i=1}^{n}\left | x_{i} \right | ∥x∥1=i=1∑n∣xi∣ - L2 范数也叫欧几里得距离,是向量元素平⽅和的平⽅根: ∥ x ∥ 2 = ∑ i = 1 n x i 2 , x ∈ R n \left \| x \right \|_{2}=\sqrt{\sum_{i=1}^{n} x_{i}^{2}},x\in \mathbb{R}^{n} ∥x∥2=i=1∑nxi2,x∈Rn
在L2 范数中常常省略下标2,也就是说 ∥ x ∥ \left \| x \right \| ∥x∥等同于 ∥ x ∥ 2 \left \| x \right \|_{2} ∥x∥2 - 类似于向量的L2 范数,矩阵 X ∈ R m × n X\in \mathbb{R}^{m\times n} X∈Rm×n 的Frobenius norm(弗罗贝尼乌斯范数)是矩阵元素平⽅和的平⽅根:
∥ X ∥ F = ∑ i = 1 m ∑ j = 1 n x i j 2 , X ∈ R m × n \left \| X \right \|_{F}=\sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n} x_{ij}^{2}},X\in \mathbb{R}^{m\times n} ∥X∥F=i=1∑mj=1∑nxij2,X∈Rm×n
代码演示:
u = torch.tensor([3.0, -4.0])
torch.abs(u).sum()#L1范数
torch.norm(u)#L2范数
tensor(5.)
tensor(7.)
torch.norm(torch.ones((4, 9)))#矩阵L2范数
tensor(6.)
2.6 向量点积、乘积和张量的缩并einsum
2.6.1 向量点积(DotProduct、点乘、内积、数量积)
向量点积其实就是类似加权求和,结果是一个标量。
- 给定两个向量 x , y ∈ R d x,y\in \mathbb{R}^{d} x,y∈Rd,它们的点积(dot product) x T y x^{T}y xTy 或⟨x,y⟩是相同位置的按元素乘积的和: x ⋅ y = x T y = ∑ i = 1 d x i y i x\cdot y=x^{T}y=\sum_{i=1}^{d}x_{i}y_{i} x⋅y=xTy=∑i=1dxiyi,所以结果是一个标量。
- 当 x x x表示一组向量, y y y为权重时, x x x的加权和可以表⽰为点积 x ⋅ y x\cdot y x⋅y。当权重为⾮负数且和时,点积表⽰加权平均(weighted average)。
x = torch.arange(4, dtype=torch.float32)
y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)
(tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))
- 点乘的几何意义
点乘的几何意义是可以用来表征或计算两个向量之间的夹角,以及在b向量在a向量方向上的投影,有公式: x ⋅ y = ∣ x ∣ ∣ y ∣ c o s θ x\cdot y=\left | x \right |\left | y \right |cos\theta x⋅y=∣x∣∣y∣cosθ
根据这个公式就可以计算向量a和向量b之间的夹角。从而就可以进一步判断这两个向量是否是同一方向,是否正交(也就是垂直)等方向关系,具体对应关系为:
- a·b>0 方向基本相同,夹角在0°到90°之间
- a·b=0 正交,相互垂直
- a·b<0 方向基本相反,夹角在90°到180°之间
2.6.2 矩阵-向量积
类似矩阵每一行进行加权求和,结果是一个向量(长度等于矩阵行数)。
对于矩阵 A ∈ R m × n A\in \mathbb{R}^{m\times n} A∈Rm×n和向量 x ∈ R n x\in \mathbb{R}^{n} x∈Rn,使用行向量表示矩阵 A A A:
A = [ a 1 T a 2 T . . . a m T ] A=\begin{bmatrix} a_{1}^{T}\\ a_{2}^{T}\\ ...\\ a_{m}^{T}\end{bmatrix} A=⎣⎢⎢⎡a1Ta2T...amT⎦⎥⎥⎤
每个 a i T a_{i}^{T} aiT都是⾏向量,表示矩阵的第i⾏。矩阵向量积 A x Ax Ax是⼀个⻓度为m的列向量,其第i个元素是点积 a i T x a_{i}^{T}x aiTx:
A x = [ a 1 T a 2 T . . . a m T ] x = [ a 1 T x a 2 T x . . . a m T x ] Ax=\begin{bmatrix} a_{1}^{T}\\ a_{2}^{T}\\ ...\\ a_{m}^{T}\end{bmatrix}x=\begin{bmatrix} a_{1}^{T}x\\ a_{2}^{T}x\\ ...\\ a_{m}^{T}x\end{bmatrix} Ax=⎣⎢⎢⎡a1Ta2T...amT⎦⎥⎥⎤x=⎣⎢⎢⎡a1Txa2Tx...amTx⎦⎥⎥⎤
调⽤torch.mv(A, x)时,会执⾏矩阵-向量积。A的列维数必须与x的维数相同。
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
x = torch.arange(4, dtype=torch.float32)
print(A)
print(x)
torch.mv(A, x)
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
tensor([0., 1., 2., 3.])
tensor([ 14., 38., 62., 86., 110.])
2.6.3 矩阵-矩阵乘法
矩阵-矩阵乘法是一个矩阵的行和另一个矩阵的列的点乘,结果是一个矩阵。
假设我们有两个矩阵 A ∈ R n × k A\in \mathbb{R}^{n\times k} A∈Rn×k 和 B ∈ R k × m B\in \mathbb{R}^{k\times m} B∈Rk×m,矩阵乘积是A的⾏向量和B的列向量做点积,结果 C ∈ R n × m C\in \mathbb{R}^{n\times m} C∈Rn×m:

矩阵-矩阵乘法AB看作是简单地执⾏m次矩阵-向量积,并将结果拼接在⼀起,形成⼀个n × m矩阵,在pytorch中,矩阵乘法可以用a.mm(b)或者torch.mm(a,b)或者a@b或者torch.matmul(t,q)三种形式,a@b最好用。
t=torch.randint(1,100,(3,4))
q=torch.randint(1,100,(4,3))
print(t)
print(q)
#三种写法都是得到3×3的矩阵
t.mm(q)#或者torch.mm(t,q)或者t@q
tensor([[90, 86, 93, 73],
[90, 84, 5, 64],
[25, 34, 17, 20]])
tensor([[50, 6, 74],
[46, 33, 93],
[76, 45, 61],
[58, 86, 99]])
tensor([[19758, 13841, 27558],
[12456, 9041, 21113],
[ 5266, 3757, 8029]])
- 一个batch矩阵的乘法,需要用bmm函数。即两个批次的矩阵乘法,是沿着批次方向分别对两个矩阵做乘法,最后将矩阵组合在一起。
- 比如一个b×m×k的矩阵和一个b×k×n的矩阵,做张量相乘,得到b×m×n的张量。
a = torch.randn(2,3,4) # 随机产生张量
c = torch.randn(2,4,3)
a.bmm(c) # 批次矩阵乘法的结果
torch.bmm(a,c)
a@b
如果是3维以上张量的乘积,称为缩并。需要用到爱因斯坦求和约定。对应函数为torch.einsum。
2.6.4 向量的普通乘积
普通乘积:对应元素相乘,结果还是向量
x ∗ y = ( x 1 y 1 , x 2 y 2 , x 3 y 3 ) x*y=(x_{1}y_{1},x_{2}y_{2},x_{3}y_{3}) x∗y=(x1y1,x2y2,x3y3)
2.6.5 矩阵的Hadamard积
- Hadamard积是两个矩阵对应位置相乘,结果还是一个矩阵,形状不变。
- 两个矩阵的按元素乘法称为Hadamard积(Hadamardproduc,数学符号⊙)。对于矩阵 A , B ∈ R m × n A,B\in \mathbb{R}^{m\times n} A,B∈Rm×n,其Hadamard积为:
A ⊙ B = [ a 11 b 11 a 12 b 12 . . . a 1 n b 1 n a 21 b 21 a 22 b 22 . . . a 2 n b 2 n . . . . . . . . . . . . a m 1 b m 1 a m 2 b m 2 . . . a m n b m n ] A\odot B=\begin{bmatrix} a_{11}b_{11}& a_{12}b_{12} & ... & a_{1n}b_{1n} \\ a_{21}b_{21}& a_{22}b_{22} & ... & a_{2n}b_{2n} \\ ...& ... &... &... \\ a_{m1}b_{m1}& a_{m2}b_{m2} & ... & a_{mn}b_{mn} \end{bmatrix} A⊙B=⎣⎢⎢⎡a11b11a21b21...am1bm1a12b12a22b22...am2bm2............a1nb1na2nb2n...amnbmn⎦⎥⎥⎤
A=torch.randint(1,10,(3,4))
B=torch.randint(1,10,(3,4))
print(A)
print(B)
A*B
tensor([[8, 3, 2, 3],
[7, 5, 8, 6],
[9, 7, 7, 6]])
tensor([[4, 4, 5, 1],
[6, 2, 5, 7],
[6, 2, 6, 6]])
tensor([[32, 12, 10, 3],
[42, 10, 40, 42],
[54, 14, 42, 36]])
2.6.4 向量的外积
两个向量的叉乘,又叫向量积、外积、叉积(Cross product),叉乘的运算结果是一个矩阵而不是一个标量。其方向与这两个向量组成的坐标平面垂直。其定义为:
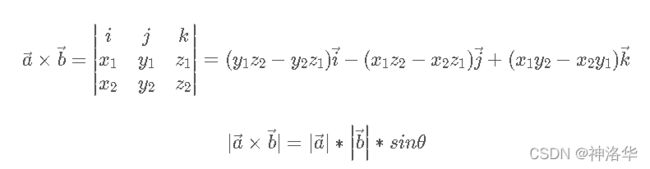
叉乘的几何定义:
方向为垂直两个向量组成的平面的方向(法向量的方向)。大小为:
→ a × → b = ∣ → a ∣ ∣ → b ∣ s i n θ \underset{a}{\rightarrow}\times \underset{b}{\rightarrow}=\left | \underset{a}{\rightarrow} \right |\left |\underset{ b}{\rightarrow} \right |sin\theta a→×b→=∣∣∣a→∣∣∣∣∣∣∣b→∣∣∣∣sinθ
| 类型 | 维度 | pythorch代码 | 说明 |
|---|---|---|---|
| 向量点积 x ⋅ y x\cdot y x⋅y | x , y ∈ R d x,y\in \mathbb{R}^{d} x,y∈Rd | torch.dot(x, y),x.dot(y) ,x.inner(y),x.matmul(x) | 类似向量加权求和,结果是标量 |
| 矩阵向量点积 y = A ⋅ x y=A\cdot x y=A⋅x | A ∈ R m × n A\in \mathbb{R}^{m\times n} A∈Rm×n, x ∈ R n x\in \mathbb{R}^{n} x∈Rn, y ∈ R m y\in \mathbb{R}^{m} y∈Rm | torch.mv(A, x),A.mv(x),A.inner(x),A.matmul(x) | 矩阵每一行对x的加权求和,结果是一个向量。 |
| 矩阵-矩阵乘法 C = A B C=AB C=AB | A ∈ R n × k A\in \mathbb{R}^{n\times k} A∈Rn×k , B ∈ R k × m B\in \mathbb{R}^{k\times m} B∈Rk×m, C ∈ R n × m C\in \mathbb{R}^{n\times m} C∈Rn×m | A@B,A.mm(B),torch.mm(A,B),torch.matmul(A,B) | 矩阵的行乘以另一个矩阵的列 |
| 向量普通乘积z=x*y | x , y , z ∈ R d x,y,z\in \mathbb{R}^{d} x,y,z∈Rd | x*y或者x.multiply(y) | 向量按位相乘,结果是一个形状不变的向量 |
| 矩阵向量普通乘积 C = A ∗ x C=A*x C=A∗x | A , C ∈ R m × n , x ∈ R n A,C\in \mathbb{R}^{m\times n},x\in \mathbb{R}^{n} A,C∈Rm×n,x∈Rn | A*x或者A.multiply(x) | 向量乘以矩阵的每一行,矩阵形状不变 |
| 矩阵乘法或矩阵Hadamard积 C = A ⊙ B C=A\odot B C=A⊙B | A , B , C ∈ R m × n A,B,C\in \mathbb{R}^{m\times n} A,B,C∈Rm×n | A*B或torch.multiply(A,A) | 两个矩阵对应位置相乘,结果还是一个矩阵,形状不变 |
| 向量的外积 x × y x\times y x×y | x , y ∈ R d x,y\in \mathbb{R}^{d} x,y∈Rd | x.outer(y) | 列向量乘以行向量,结果是一个矩阵 |
| 代码 | 说明 |
|---|---|
| torch.dot(x,y) | 计算两个一维张量的点积 |
| torch.mv(A,x) | 只能计算一个向量和一个矩阵的点积 |
| torch.matmul(A,B) | 1.2.多维张量的矩阵乘积,具体看文档 |
| torch.inner(A,B) | 计算1.2.多维张量内积 |
| torch.outer(x,y) | 只能计算两个向量的外积 |
| torch.multiply或者* | 1.2.多维张量间的普通乘积,按位相乘,形状不变 |
2.7 张量的拼接和分割split
torch.stack:传入张量列表和维度,将张量沿此维度进行堆叠(新建一个维度来堆叠)
torch.cat:传入张量列表和维度,将张量沿此维度进行堆叠
两个都是拼接张量,torch.stack会新建一个维度来拼接,后者维度预先存在,沿着此维度堆叠就行。
t1 = torch.randn(3,4) # 随机产生三个张量
t2 = torch.randn(3,4)
t3 = torch.randn(3,4)
torch.stack([t1,t2,t3], -1).shape# 沿着最后一个维度做堆叠,返回大小为3×4×3的张量
torch.Size([3, 4, 3])
-----------------------------------------------------------------------------
torch.cat([t1,t2,t3], -1).shape # 沿着最后一个维度做拼接,返回大小为3×14的张量
torch.Size([3, 12])
torch.split(tensor, split_size_or_sections, dim=0)
torch.split函数,有三个参数。将张量沿着指定维度进行分割。
第二个参数可以是整数n或者列表list。前者表示这个维度等分成n份(最后一份可以是剩余的)。或者表示分成列表元素值来分割。
torch.chunk函数和slpit函数类似
t = torch.randint(1, 10,(3,6)) # 随机产生一个3×6的张量
tensor([[8, 9, 5, 3, 6, 7],
[1, 4, 2, 2, 7, 1],
[5, 2, 5, 7, 2, 7]])
------------------------------------------------------------------------------
t.split([1,2,3], -1) # 把张量沿着最后一个维度分割为三个张量
(tensor([[8],
[1],
[5]]),
tensor([[9, 5],
[4, 2],
[2, 5]]),
tensor([[3, 6, 7],
[2, 7, 1],
[7, 2, 7]]))
------------------------------------------------------------------------------
t.split(3, -1) # 把张量沿着最后一个维度分割,分割大小为3,输出的张量大小均为3×3
(tensor([[8, 9, 5],
[1, 4, 2],
[5, 2, 5]]),
tensor([[3, 6, 7],
[2, 7, 1],
[7, 2, 7]]))
t.chunk(3, -1) # 把张量沿着最后一个维度分割为三个张量,大小均为3×2
(tensor([[8, 9],
[1, 4],
[5, 2]]),
tensor([[5, 3],
[2, 2],
[5, 7]]),
tensor([[6, 7],
[7, 1],
[2, 7]]))
2.8 张量扩增(unsqueeze)、压缩(squeeze)和广播
- 张量可以任意扩增一个维度大小为1 的维度,数据不变。反过来这些维度大小为1的维度也可以压缩掉。
t = torch.rand(3, 4) # 随机生成一个张量
t.unsqueeze(-1).shape # 扩增最后一个维度
torch.Size([3, 4, 1])
t.unsqueeze(-1).unsqueeze(1).shape # 继续扩增一个维度
torch.Size([3, 1, 4, 1])
t = torch.rand(1,3,4,1) # 随机生成一个张量,有两个维度大小为1
t.squeeze().shape # 压缩所有大小为1的维度
torch.Size([3, 4])
- 两个不同维度的张量做四则运算,需要先把维度数目少的张量扩增到和另一个一致(unsqueeze方法),再进行运算。运算时,将扩增的维度进行复制,到最后维度一致再运算。
t1 = torch.randn(3,4,5)
t2 = torch.randn(3,5)
t2 = t2.unsqueeze(1) # 张量2的形状变为3×1×5
print(t2)
tensor([[[ 0.7188, -1.1053, -0.1161, -2.2889, -0.8046]],
[[ 0.1434, -2.8369, -1.5712, 1.1490, 0.7161]],
[[-0.8259, 1.8744, -0.7918, -0.4208, 1.6935]]])
t3 = t1 + t2 #将t2沿着第二个维度复制4次,最后形状为(3,4,5)
print(t3)
tensor([[[ 1.6212, -1.0232, 1.9735, -2.3579, -2.8416],
[ 1.3389, -0.7377, -0.8453, -2.2385, -1.4370],
[ 1.4433, -1.8982, -0.0669, -2.8503, -1.0240],
[-0.0498, -2.2708, 0.4583, -0.3370, -2.7074]],
[[ 1.7768, -2.4552, 0.3409, -0.7948, 1.9718],
[ 0.1147, -3.2569, -1.4112, 1.3465, 0.2129],
[ 0.8951, -3.5355, -0.3349, 1.4523, 0.2659],
[ 0.6704, -2.3110, -1.1827, 0.8700, 2.9844]],
[[-0.3561, 0.7850, -0.9848, -0.8666, 0.0758],
[-0.1744, 1.3592, -1.7955, -0.0697, 3.8696],
[-2.5559, 2.6479, -0.1718, -0.2446, 1.7351],
[ 0.5748, 1.2866, -1.3801, 0.0290, 1.0740]]])
在大多数情况下,我们将沿着数组中长度为1的轴进行广播,如下例子:
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
print(a)
print(b)
a+b
(tensor([[0],
[1],
[2]]),
tensor([[0, 1]]))
tensor([[0, 1],
[1, 2],
[2, 3]])
所以有时候我们没想做广播,只是把张量相加,结果成了一个矩阵。这时候应该考虑是不是做了广播。
2.9 原地操作
运行一些操作可能会导致为新结果分配内存。 例如,如果我们用Y = X + Y,将会为Y分配新的内存。
before = id(Y)
Y = Y + X
id(Y) == before
False
这可能是不可取的,原因有两个:
- 首先,我们不想总是不必要地分配内存。 在机器学习中,我们可能有数百兆的参数,并且在一秒内多次更新所有参数。 通常情况下,我们希望原地执行这些更新。
- 其次,如果我们不原地更新,其他引用仍然会指向旧的内存位置, 这样我们的某些代码可能会无意中引用旧的参数
- 原地操作:可以使用切片表示法将操作的结果分配给先前分配的数组。例如X[:] = X + Y或X += Y来减少操作的内存开销。
- 原地修改可能会修改原先的数据,例如:
a=torch.arange(12)
b=a.reshape(3,4)
b[:]=1
a
tensor([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
三. PyTorch 自动微分
3.1 autograd 自动求导和冻结参数
- autograd 软件包为 Tensors 上的所有操作提供自动微分,是 PyTorch 中所有神经网络的核心。
- 设置torch.Tensor 类的属性 .requires_grad = True,则表示该张量会加入到计算图中,作为叶子节点参与计算,自动跟踪针对 tensor的所有操作。计算的中间结果都是requires_grad = True。
- 每个张量都有一个 grad_fn方法,保存创建该张量的运算的导数信息、计算图信息。
- 调用 Tensor.backward() 传入最后一层的神经网络梯度。grad_fn方法的 next.functions属性,包含连接该张量的其它张量的grad_fn。不断反向传播回溯中间张量计算节点,可以得到所有张量的梯度。该张量的梯度将累积到 .grad 属性 中。如果Tensor 是标量,则backward()不需要指定任何参数。否则,需要指定一个gradient 参数来指定张量的形状。
- with torch.no_grad() : 包装的代码块部分,停止跟踪历史记录(和使用内存)。
- 张量绑定的梯度在不清空的情况下会不断累积。可用来一次性求很多batch的累积梯度。
Tensor 和 Function 互相连接并构建一个非循环图,它保存整个完整的计算过程的历史信息。每个张量都有一个 .grad_fn 属性保存着创建了张量的 Function 的引用,(如果用户自己创建张量,则g rad_fn 是 None )。
x = torch.ones(2, 2, requires_grad=True)
y = x + 2
z = y * y * 3
out = z.mean()
print(z, out)
tensor([[27., 27.],
[27., 27.]], grad_fn=<MulBackward0>)
tensor(27., grad_fn=<MeanBackward0>)
out.backward()
print(x.grad)
tensor([[4.5000, 4.5000],
[4.5000, 4.5000]])
- 冻结参数
在 torch.nn 中,不计算梯度的参数通常称为冻结参数。 如果事先知道您不需要这些参数的梯度,则“冻结”模型的一部分很有用(通过减少自动梯度计算,这会带来一些表现优势)。
例如加载一个预训练的 resnet18 模型,并冻结所有参数,仅修改分类器层以对新标签进行预测。
from torch import nn, optim
model = torchvision.models.resnet18(pretrained=True)
# 冻结网络的所有参数
for param in model.parameters():
param.requires_grad = False
假设我们要在具有 10 个标签的新数据集中微调模型。 在 resnet 中,分类器是最后一个线性层model.fc。 我们可以简单地将其替换为充当我们的分类器的新线性层(默认情况下未冻结)。
model.fc = nn.Linear(512, 10)
# Optimize only the classifier
optimizer = optim.SGD(model.fc.parameters(), lr=1e-2, momentum=0.9)
现在,除了model.fc的参数外,模型中的所有参数都将冻结。 计算梯度的唯一参数是model.fc的权重和偏差。(torch.no_grad()中的上下文管理器可以使用相同的排除功能。)
3.2 雅克比向量积
3.3 计算图
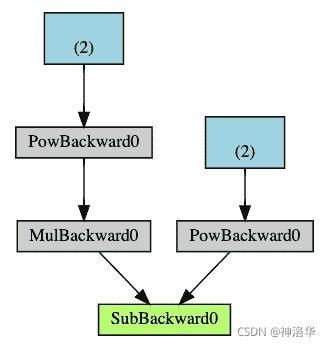
Autograd 在由函数对象组成的有向无环图(DAG)中记录张量、所有已执行的操作(以及由此产生的新张量)。 在此 DAG 中,叶子是输入张量,根是输出张量。 通过从根到叶跟踪此图,可以使用链式规则自动计算梯度。
-
在正向传播中,Autograd 同时执行两项操作:
- 根据张量和function计算结果张量
- 在 DAG 中维护操作的梯度函数。
-
当在 DAG 根目录上调用.backward()时,开始回传梯度,然后:
- 从每个.grad_fn计算梯度,将它们累积在各自的张量的.grad属性中
- 使用链式规则,一直传播到叶子张量。
下面是我们示例中 DAG 的直观表示。 在图中,箭头指向前进的方向。 节点代表正向传播中每个操作的反向函数。 蓝色的叶节点代表我们的叶张量a和b: