pytorch转置卷积（ConvTranspose）详解
目录
说明
用矩阵乘法实现卷积
第一步
第二步
第三步
第四步
转置卷积
参数padding
参数stride和output_padding（情况一）
参数stride和output_padding（情况二）
参数dilation
卷积+转置卷积做因果网络
说明
开始接触卷积网络是通过滑窗的方式了解计算过程，所以在接触转置卷积时很蒙圈。
实际上抛开滑窗的计算方式，用矩阵乘法实现卷积操作，然后理解转置卷积就极其简单了。
并没有查看pytorch源码，有任何问题欢迎指正。
前置知识：明白卷积的滑窗计算过程。
用矩阵乘法实现卷积
这里用二维卷积来举例，为方便观察，把batch size和输入输出通道数都设为1。
首先从最简单的情况开始，stride=[1, 1]，dilation=[1, 1]，padding=[0, 0]。
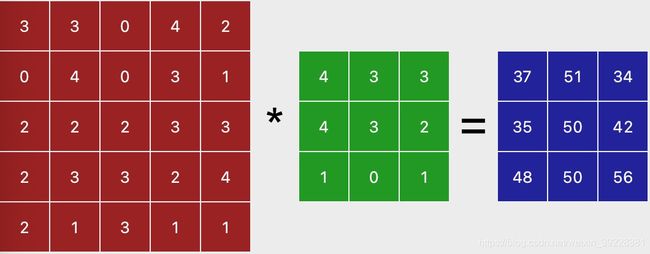
此时，如果我们输入5*5的图片，卷积核是3*3，则显然输出尺寸是3*3，如下图所示，红色是输入，绿色是卷积核，蓝色是输出。
接下来把上述过程用矩阵乘法来实现。
第一步
由于padding是[0, 0]，所以最终的输入尺寸是5*5，把卷积核放在5*5的格子里按照stride=[1, 1]滑动（注意这里仅仅是在5*5的格子里滑动，不是在输入矩阵上滑动），每次滑动都在卷积核四周补零，得到5*5的矩阵，如下图，分别是第一次，第二次和最后一次滑动时的补零情况，其中浅绿色部分是补充的0。有多少次滑动，就有多少次补零，于是最终得到9个补零后的矩阵。
第二步
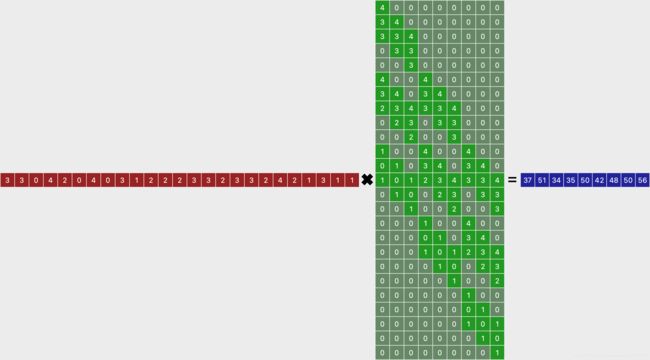
把每个补零后的矩阵都flatten成列向量，维度是25*1；然后把9个向量按序拼成一个矩阵，维度是25*9，如下图。
第三步
把输入矩阵flatten成一个行向量，维度是1*25，然后和第二步的矩阵（维度是25*9）做矩阵乘法，即完成卷积操作，如下图。
注意这里的尺寸细节：卷机核是在5*5的格子里滑动，每次补零成5*5的矩阵，最终flatten成25*1的列向量，多次滑动，flatten后，得到N个25*1列向量，合成25*N矩阵；之所以在5*5的格子里滑动，是因为输入是5*5的，所以最终才能做矩阵乘法。
第四步
把蓝色的输出reshape成正确的size即可。计算公式是：![{\color{Blue} H_{out}=\frac{H_{in}-kernel\_size[0]}{stride[0]}+1, W_{out}=\frac{W_{in}-kernel\_size[1]]}{stride[1]}+1}](http://img.e-com-net.com/image/info8/6e9c2bf6bf714d438a26041726c19d86.gif){kind=small}
。注意：这里的
和
都是padding之后的（本例的padding=[0, 0]），这个公式很容易懂，举几个具体的例子即可。
转置卷积
有了上边的基础，理解转置卷积就非常容易了。
转置卷积通常是跟在卷积之后（不一定直接相连，但是是一一对应的，如CRN网络），转置卷积的输入输出尺寸，应该和对应的卷积的输入输出尺寸是相反的（这应该就是为什么转置卷积还叫做反卷机或者逆卷积的原因吧），即如果卷积输入5*5，输出3*3时，转置卷机是输入3*3，输出5*5。即上述蓝色公式的反函数：![{\color{Purple} H_{in}=(H_{out}-1)*stride[0] + kernel\_size[0], W_{in}=(W_{out}-1)*stride[1] + kernel\_size[1]}](http://img.e-com-net.com/image/info8/00ee274d2f9e456fa3ab6c38459c7cef.gif){kind=small}
。为了方便，把参数名字改一下：![{\color{Red} H_{out}=(H_{in}-1)*stride[0] + kernel\_size[0], W_{out}=(W_{in}-1)*stride[1] + kernel\_size[1]}](http://img.e-com-net.com/image/info8/9aade102c1724a8dbab92e5d94221494.gif){kind=small}
。注意：这里红色的
和
是转置卷积的输入尺寸，也是对应的卷积的输出尺寸；我们计算得到的红色的
和
是没有经过转置卷积的padding和output_padding的，这里先不考虑padding和output_padding，所以这里和等于5*5，然后卷积核在5*5的格子里滑动，补零，flatten，然后合成25*9的矩阵。
接下来就是灵魂操作，把25*9的矩阵转置一下，得到9*25，然后输入矩阵是3*3，flatten成1*9的行向量，做矩阵乘法，得到1*25的输出，再reshape成
，即5*5。
至此转置卷机就完成了。和卷积最大的不同有两点：第一，转换卷积核时，在H*W的格子里滑动，这个H和W的计算来源不同，但是却是相等的；第二，转置卷积把卷积核转换成矩阵后，需要进行转置。
参数padding
现在来看下两种卷积中的padding参数，stride依旧是[1, 1]，转置卷积中的output_padding依旧是[0, 0]。
在卷积时，为了保证输入输出尺寸不变，需要padding，比如3*3的卷积核，需要padding=[1, 1]，才能保证输出和输入一样。
在转置卷机中，如果padding=[0, 0]，则输入5*5则会输出7*7（见上述讲解）。所以在转置卷积中padding实际上的作用是减小输出尺寸。来看下是怎么做到的：首先不考虑padding，然后得到7*7的结果，由于padding=[1, 1]（和对应的卷积中的padding保持一致），即把结果的两个维度的两边都砍掉1，就变成了5*5。
注意：这里的解释和pytorch的官方文档不一致，但是通过自己实现的转置卷积代码（https://github.com/zcsxll/test_pytorch/blob/main/test_ConvTranspose2d.py）验证，结果和torch.nn.ConvTranspose2d一致。
参数stride和output_padding（情况一）
如果stride大于1，这里用stride=[2, 2]举例，卷积输入5*5，则输出2*2。
转置卷积输入2*2，根据上述红色公式，![H_{out}=(H_{in}-1)*stride[0] + kernel\_size[0]=(2-1)*2+3=5](http://img.e-com-net.com/image/info8/40fe7399ad2440a195d57fb3d67cd8ce.gif){kind=small}
，然后在5*5的格子里按stride=[2, 2]滑动卷积核，补零，flatten，然后合成25*4的矩阵，再转置一下得到4*25的矩阵，最后把输入2*2flatten成1*4，然后做矩阵乘法，得到1*25，最后reshape成5*5。
此时和stride=[1, 1]没有区别。
参数stride和output_padding（情况二）
如果stride大于1，这里用stride=[2, 2]举例，卷积输入6*6，则输出还是2*2。
转置卷积输入2*2，根据上述红色公式，，然后在5*5的格子里按stride=[2, 2]滑动卷积核，补零，flatten，然后合成25*4的矩阵，在把输入2*2flatten成1*4，然后做矩阵乘法，得到1*25，最后reshape成5*5。
此时出现问题，我们应该通过转置卷积把2*2变成6*6的结果才对，所以需要使用output_padding，这个参数需要我们自己计算出来，注意output_padding不是在每个维度的两边都加1，而是只在后面加1，所以显然这里是output_padding=[1, 1]，则从 5*5变成了6*6，然后在6*6的格子里按stride=[2, 2]滑动卷积核，补零，flatten（这时flatten后，得到列向量是36*1的），然后合成36*4的矩阵，再转置一下得到4*36的矩阵，最后把输入2*2flatten成1*4，然后做矩阵乘法，得到1*36，最后reshape成6*6。
所以output_padding是转置卷积独有的参数，卷积没有这个参数，只有padding。
参数dilation
这个参数是为了不增加参数量和计算量的情况下，增大感受野。通过向卷积核中见插入0的方式把卷积核变大了，进而感受野就大了，这个参数对于理解转置卷积没有什么影响。
卷积+转置卷积做因果网络
对图片的卷积可以使用自带的padding和output_padding，但是对于时间T上的卷积，则不使用自带的padding和output_padding。需要在输入到卷积之前，手动padding，然后在转置卷积输出之后，进行手动切除。
为了方便，用一维卷积举例，卷积核=3，stride=1。输入前边需要补充3-1=2个零，如下图左下角的pad；然后进行卷积+转置卷积，最后把输出的后两个
cut掉，即输出是
。此时输出的
只依赖中间部分的第1个隐藏特征（下图中间一共有3个隐藏特征），而第1个隐藏特征只依赖pad的两个0以及
，并不依赖
；同理输出的
依赖前两个隐藏特征，而这两个隐藏特征来自于pad的两个0以及
，并不依赖
；这样的网络即为因果网络，因为每一个输出都不需要使用未来信息。
如果我们不使用，而是使用
作为输出，即每一个输出都使用了未来信息，那么我们让去拟合真实label，则很大程度上能改善网络效果，但是做不到实时处理了，需要延迟一帧输出。