逻辑斯蒂回归原理及梯度下降法python实现
逻辑斯蒂回归
回归与分类的转换
- 回归:学习得到一个函数将输入变量映射到连续输出空间,即值域是连续空间
- 分类:学习得到一个函数将输入变量映射到离散输出空间,即值域是离散空间
回顾感知机
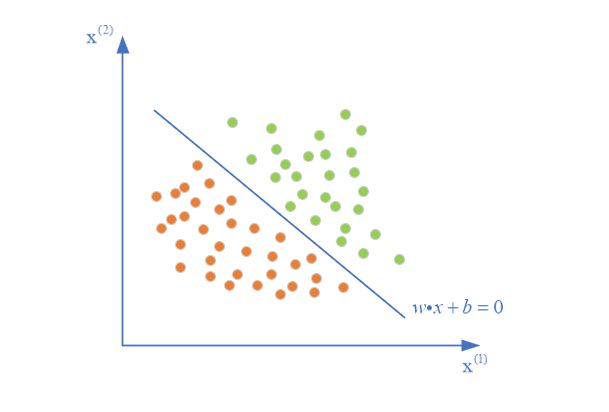
感知机模型用一个超平面 w ⋅ x + b = 0 w \cdot x+b=0 w⋅x+b=0将实例点二分成两个类别 + 1 +1 +1和 − 1 -1 −1
其最终分类的函数为
f ( x ) = s i g n ( w ⋅ x + b ) f(x)=sign(w·x+b) f(x)=sign(w⋅x+b)
其中
s i g n ( x ) = { + 1 , x > = 0 − 1 , x < 0 (2) sign(x) = \left\{ \begin{aligned} +1,\ & x>=0\\ -1,\ & x<0\\ \end{aligned} \right.\tag{2} sign(x)={+1, −1, x>=0x<0(2)
则输入经过 w ⋅ x + b w\cdot x+b w⋅x+b得到连续输出的过程是回归过程,将回归结果使用 s i g n sign sign函数转换成离散值实现了分类
所以感知机其实是一种由回归到分类得模型,而逻辑斯蒂回归与感知机一样,都是由回归到分类的转换
感知机的问题
通过感知机模型可以发现,感知机最后输出的结果只有 1 1 1和 − 1 -1 −1,也就是两个类别,这是比较绝对的
即使在超平面两边非常相近地两个点,感知机也觉他们就是完全不同类的
如果最后能输出分到某个类别的置信程度,再根据置信程度大小将其分到该类别,则能解决绝对的问题
这当然不是直接输出 w ⋅ x + b w\cdot x+b w⋅x+b的值,该回归值的范围太大了,为 ( − ∞ , + ∞ ) (-\infin,+\infin) (−∞,+∞),可以考虑将其映射到一个更小的范围
感知机的缺陷
观察感知机模型 f ( x ) = s i g n ( w ⋅ x + b ) f(x)=sign(w·x+b) f(x)=sign(w⋅x+b)可知,最终得到的预测函数 f ( x ) f(x) f(x)是间断的,非连续的,在 w ⋅ x + b = 0 w\cdot x+b=0 w⋅x+b=0处是不可微的,所以在感知机利用损失函数求参数 w w w时,需要脱去 s i g n sign sign考虑 w ⋅ x + b w\cdot x+b w⋅x+b
能否找到一个更好的连续可微模型代替感知机呢?逻辑斯蒂回归就较好地弥补了感知机的缺陷
s i g m o i d sigmoid sigmoid函数
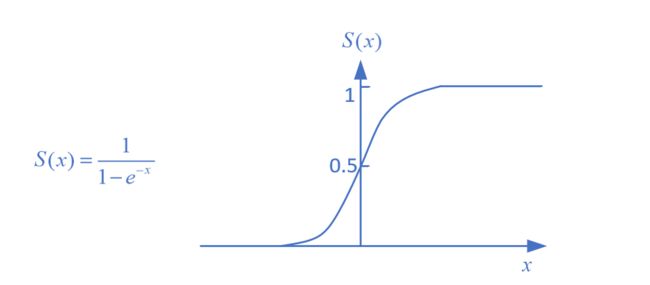
s i g m o i d sigmoid sigmoid函数以及其图像如下
由 s i g m o i d sigmoid sigmoid函数我们可以观察到
-
其定义域 ( − ∞ , + ∞ ) (-\infin,+\infin) (−∞,+∞),值域为(0,1),连续可微
-
当输入 x → − ∞ x\rightarrow{-\infin} x→−∞时, S ( x ) → 0 S(x)\rightarrow0 S(x)→0
-
当 x → + ∞ x\rightarrow{+\infin} x→+∞, S ( x ) → 1 S(x)\rightarrow1 S(x)→1
若将感知机中回归结果 w ⋅ x + b w\cdot x+b w⋅x+b带入 s i g m o i d sigmoid sigmoid函数如下
S ( w ⋅ x + b ) = e w ⋅ x + b 1 + e w ⋅ x + b S(w\cdot x+b)=\frac{e^{w\cdot x+b}}{1+e^{w\cdot x+b}} S(w⋅x+b)=1+ew⋅x+bew⋅x+b
其有如下特点
- w ⋅ x + b ∈ ( − ∞ , + ∞ ) w\cdot x+b \in (-\infin,+\infin) w⋅x+b∈(−∞,+∞)
- 当 w ⋅ x + b > 0 w\cdot x+b>0 w⋅x+b>0时, S ( w ⋅ x + b ) > 0.5 S(w\cdot x+b)>0.5 S(w⋅x+b)>0.5
- 当 w ⋅ x + b = 0 w\cdot x+b=0 w⋅x+b=0时, S ( w ⋅ x + b ) = 0.5 S(w\cdot x+b)=0.5 S(w⋅x+b)=0.5
- 当 w ⋅ x + b < 0 w\cdot x+b<0 w⋅x+b<0时, S ( w ⋅ x + b ) < 0.5 S(w\cdot x+b)<0.5 S(w⋅x+b)<0.5
在感知机中,当 w ⋅ x + b > 0 w\cdot x+b>0 w⋅x+b>0时, s i g n sign sign的输出直接为其分类 + 1 +1 +1;而在 s i g m o i d sigmoid sigmoid函数中,输出为一个值 S ( w ⋅ x + b ) > 0.5 S(w\cdot x+b)>0.5 S(w⋅x+b)>0.5
在感知机中,当 w ⋅ x + b < 0 w\cdot x+b<0 w⋅x+b<0时, s i g n sign sign的输出直接为其分类 − 1 -1 −1;而在 s i g m o i d sigmoid sigmoid函数中,输出为一个值 S ( w ⋅ x + b ) < 0.5 S(w\cdot x+b)<0.5 S(w⋅x+b)<0.5
则考虑能否将 S ( w ⋅ x + b ) S(w\cdot x+b) S(w⋅x+b)表示为给定输入 x x x被分类为 + 1 +1 +1的概率 P ( Y = + 1 ∣ x ) P(Y=+1|x) P(Y=+1∣x),当概率大于0.5时,将 x x x分类为 + 1 +1 +1;当概率小于0.5时候,将 x x x分类为 − 1 -1 −1
根据这个想法便可以利用连续的 s i g m o d sigmod sigmod函数代替间断的 s i g n sign sign函数;最终输出的是分类到某个类的概率,避免了绝对的输出;并且也得到了我们想要的置信度
w ⋅ x + b w\cdot x+b w⋅x+b越接近 + ∞ +\infin +∞, P ( Y = + 1 ∣ x ) P(Y=+1|x) P(Y=+1∣x)越接近 1 1 1,则将 x x x分类到 + 1 +1 +1的可信程度越大,应将其分到+1类
从超平面划分理解, w ⋅ x + b w\cdot x+b w⋅x+b距离 0 0 0越大,该实例越远离超平面,其越应被分类到某个类
逻辑斯蒂回归就是这样做的,但是其思想过程并不是上面所述,上述只是个人理解
二项逻辑斯蒂回归模型
二项即二分类
定义
二项逻辑斯蒂分布输入 x ∈ R n x\in R^n x∈Rn,输出 Y ∈ { 0 , 1 } Y \in \{0,1\} Y∈{0,1};
类别名称无所谓,可以把这里的1看作感知机中的正类,把 0 0 0看作感知机中的负类
与感知机类似, w ∈ R n w\in R^n w∈Rn和 b ∈ R n b\in R^n b∈Rn为参数,前者为权值向量,后者为偏置
其为如下的条件概率分布:
P ( Y = 1 ∣ x ) = e x p ( w ⋅ x + b ) 1 + e x p ( w ⋅ x + b ) P ( Y = 0 ∣ x ) = 1 1 + e x p ( w ⋅ x + b ) \begin{aligned} P(Y=1|x) &= \frac{exp(w\cdot x+b)}{1+exp(w\cdot x+b)}\\ P(Y=0|x)&= \frac{1}{1+exp(w\cdot x+b)} \end{aligned} P(Y=1∣x)P(Y=0∣x)=1+exp(w⋅x+b)exp(w⋅x+b)=1+exp(w⋅x+b)1
对于给定输入 x x x,根据上述式子可以求得 x x x为某类的概率,将实例分到结果较大(二分类时为结果大于 0.5 0.5 0.5)的类
特点
-
在逻辑斯蒂回归模型中,输出 Y = 1 Y=1 Y=1的对数几率是输入 x x x的线性函数
一个事件的几率是指该事件发生的额概率与该事件不发生的概率的比值
如果事件发生的概率是 p p p,那么该事件的几率是 p 1 − p \frac{p}{1-p} 1−pp
则该事件的对数几率( l o g i logi logit函数)是
l o g i t ( p ) = l o g p 1 − p logit(p)=log\frac{p}{1-p} logit(p)=log1−pp对于逻辑斯蒂回归
l o g P ( Y = 1 ∣ X ) 1 − P ( Y = 1 ∣ x ) = w ⋅ x + b log\frac{P(Y=1|X)}{1-P(Y=1|x)}=w\cdot x+b log1−P(Y=1∣x)P(Y=1∣X)=w⋅x+b
所以说,输出 Y = 1 Y=1 Y=1的对数几率是输入 x x x的线性函数 -
将线性函数转换成概率,即逻辑斯蒂回归模型
观察逻辑斯蒂回归模型,可以看到其将 w ⋅ x + b w \cdot x+b w⋅x+b转换成了概率 P ( Y = 1 ∣ x ) P(Y=1|x) P(Y=1∣x)
P ( Y = 1 ∣ x ) = e x p ( w ⋅ x + b ) 1 + e x p ( w ⋅ x + b ) P(Y=1|x) = \frac{exp(w\cdot x+b)}{1+exp(w\cdot x+b)} P(Y=1∣x)=1+exp(w⋅x+b)exp(w⋅x+b)这时,线性函数的值越接近正无穷,概率值越接近1,其越应该被分到该类;反之,线性函数的值越接近负无穷,概率值就越接近 0 0 0,其越不应该分到该类
跟介绍 s i g m o i d sigmoid sigmoid函数时我理解的类似
模型的参数估计
逻辑斯蒂回归模型学习时,对于给定的训练数据集 T = { ( x 1 , y 1 ) , ( x 1 , y 1 ) , . . . ( x N , y N ) } T=\{(x_1,y_1),(x_1,y_1),...(x_N,y_N)\} T={(x1,y1),(x1,y1),...(xN,yN)},其中 x i ∈ R n x_i \in R^{n} xi∈Rn, y i ∈ { 0 , 1 } y_i \in \{0,1\} yi∈{0,1},此时需要推出模型中的参数 w , b w,b w,b
对于概率模型,可以使用极大似然估计法估计参数
极大似然估计思想不难,B站学一下就好,博主也是现学的 q a q qaq qaq
参数估计
记
P ( Y = 1 ∣ x ) = π ( x ) P ( Y = 0 ∣ x ) = 1 − π ( x ) \begin{aligned} P(Y=1|x)&=\pi(x)\\ P(Y=0|x)&=1-\pi(x) \end{aligned} P(Y=1∣x)P(Y=0∣x)=π(x)=1−π(x)
将概率公式合并为
P ( x ) = [ π ( x ) ] y [ 1 − π ( x ) ] 1 − y P(x) =[\pi(x)]^{y}[1-\pi(x)]^{1-y} P(x)=[π(x)]y[1−π(x)]1−y
对数据集求似然函数有
∏ i = 1 N [ π ( x i ) ] y i [ 1 − π ( x i ) ] 1 − y i \prod_{i=1}^N[\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i} i=1∏N[π(xi)]yi[1−π(xi)]1−yi
对数似然函数为
L ( w , b ) = l o g { ∏ i = 1 N [ π ( x i ) ] y i [ 1 − π ( x i ) ] 1 − y i } = ∑ i = 1 N [ y i l o g π ( x i ) + ( 1 − y ) l o g ( 1 − π ( x i ) ) ] = ∑ i = 1 N [ y i l o g π ( x i ) 1 − π ( x i ) + l o g ( 1 − π ( x i ) ) ] = ∑ i = 1 N [ y i ( w ⋅ x i + b ) − l o g ( 1 + e x p ( w ⋅ x i + b ) ) ] \begin{aligned} L(w,b) &= log\{\prod_{i=1}^N[\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i}\}\\ &= \sum_{i=1}^{N}[y_ilog\pi(x_i)+(1-y)log(1-\pi(x_i))]\\ &=\sum_{i=1}^{N}[y_ilog\frac{\pi(x_i)}{1-\pi(x_i)}+log(1-\pi(x_i))]\\ &=\sum_{i=1}^{N}[y_i(w\cdot x_i+b)-log(1+exp(w\cdot x_i+b))] \end{aligned} L(w,b)=log{i=1∏N[π(xi)]yi[1−π(xi)]1−yi}=i=1∑N[yilogπ(xi)+(1−y)log(1−π(xi))]=i=1∑N[yilog1−π(xi)π(xi)+log(1−π(xi))]=i=1∑N[yi(w⋅xi+b)−log(1+exp(w⋅xi+b))]
求 L ( w , b ) L(w,b) L(w,b)的极大值即可得到 w , b w,b w,b的估计值
则最终问题变成了求以对数似然函数为目标函数的最优化问题
逻辑斯蒂回归通常采用梯度下降法及牛顿法
感知机是以损失函数为目标函数,而逻辑斯蒂回归是以似然函数为目标函数
但最终对目标函数最优的求法都可以用梯度下降
最终模型
假设 w , b w,b w,b的极大似然估计值是 w ^ , b ^ \hat w,\hat b w^,b^,那么最终学习到的逻辑斯蒂回归模型为
P ( Y = 1 ∣ x ) = e x p ( w ^ ⋅ x + b ^ ) 1 + e x p ( w ^ ⋅ x + b ^ ) P ( Y = 0 ∣ x ) = 1 1 + e x p ( w ^ ⋅ x + b ^ ) \begin{aligned} P(Y=1|x) &= \frac{exp(\hat w\cdot x+\hat b)}{1+exp(\hat w\cdot x+\hat b)}\\ P(Y=0|x) &= \frac{1}{1+exp(\hat w\cdot x+\hat b)} \end{aligned} P(Y=1∣x)P(Y=0∣x)=1+exp(w^⋅x+b^)exp(w^⋅x+b^)=1+exp(w^⋅x+b^)1
梯度下降法求解极大似然估计值
求解极大似然估计值即求解在 L ( w , b ) L(w,b) L(w,b)极大的情况下,参数 w , b w,b w,b的值,这里使用梯度下降法求解
并且由于梯度下降法是求极小值,这里将原函数取反
L ( w , b ) = − ∑ i = 1 N [ y i ( w ⋅ x i + b ) − l o g ( 1 + e x p ( w ⋅ x i + b ) ) ] L(w,b)=-\sum_{i=1}^{N}[y_i(w\cdot x_i+b)-log(1+exp(w\cdot x_i+b))] L(w,b)=−i=1∑N[yi(w⋅xi+b)−log(1+exp(w⋅xi+b))]
L ( w , b ) L(w,b) L(w,b)对 w w w求偏导有
∂ L ( w , b ) ∂ w = − ∑ i = 1 N [ y i x i − x i [ e x p ( w ⋅ x + b ) ] 1 + e x p ( w ⋅ x i + b ) ] = − ∑ i = 1 N [ y i x i − x i 1 + e x p [ − ( w ⋅ x i + b ) ] ] = ∑ i = 1 N [ S ( w ⋅ x i + b ) − y i ] x i \begin{aligned} \frac{\partial L(w,b)}{\partial w}&=-\sum_{i=1}^{N}[y_ix_i-\frac{x_i[exp(w\cdot x+b)]}{1+exp(w\cdot x_i+b)}]\\ &=-\sum_{i=1}^{N}[y_ix_i-\frac{x_i}{1+exp[-(w\cdot x_i+b)]}]\\ &=\sum_{i=1}^N[S(w\cdot x_i+b)-y_i]x_i \end{aligned} ∂w∂L(w,b)=−i=1∑N[yixi−1+exp(w⋅xi+b)xi[exp(w⋅x+b)]]=−i=1∑N[yixi−1+exp[−(w⋅xi+b)]xi]=i=1∑N[S(w⋅xi+b)−yi]xi
S为 s g m o i d sgmoid sgmoid函数
L ( w , b ) L(w,b) L(w,b)对 b b b求偏导有
∂ L ( w , b ) ∂ b = − ∑ i = 1 N [ y i x i − e x p ( w ⋅ x + b ) 1 + e x p ( w ⋅ x i + b ) ] = − ∑ i = 1 N [ y i − 1 1 + e x p [ − ( w ⋅ x i + b ) ] ] = ∑ i = 1 N [ S ( w ⋅ x i + b ) − y i ] \begin{aligned} \frac{\partial L(w,b)}{\partial b} &=-\sum_{i=1}^{N}[y_ix_i-\frac{exp(w\cdot x+b)}{1+exp(w\cdot x_i+b)}]\\ &=-\sum_{i=1}^{N}[y_i-\frac{1}{1+exp[-(w\cdot x_i+b)]}]\\ &=\sum_{i=1}^N[S(w\cdot x_i+b)-y_i] \end{aligned} ∂b∂L(w,b)=−i=1∑N[yixi−1+exp(w⋅xi+b)exp(w⋅x+b)]=−i=1∑N[yi−1+exp[−(w⋅xi+b)]1]=i=1∑N[S(w⋅xi+b)−yi]
则在梯度下降迭代的过程中,先初始化 w w w和 b b b,在迭代过程中通过上述两个梯度不断更新 w w w和 b b b,设每次更新的步长为 η \eta η,共迭代 T T T次,每次迭代过程如下
w t + 1 = w t − η ⋅ ∑ i = 1 N [ S ( w ⋅ x i + b ) − y i ] x i b t + 1 = b t − η ⋅ ∑ i = 1 N [ S ( w ⋅ x i + b ) − y i ] \begin{aligned} w^{t+1}&=w^t-\eta\cdot\sum_{i=1}^N[S(w\cdot x_i+b)-y_i]x_i\\ b^{t+1}&=b^t-\eta\cdot\sum_{i=1}^N[S(w\cdot x_i+b)-y_i] \end{aligned} wt+1bt+1=wt−η⋅i=1∑N[S(w⋅xi+b)−yi]xi=bt−η⋅i=1∑N[S(w⋅xi+b)−yi]
随得到了梯度下降的方法,但是上面还有几个不清楚的地方
-
w w w和 b b b如何初始值?
许多情况下是随机初始化 w w w和 b b b,当然如果根据经验比较清楚 w w w和 b b b可能的最优解,也可以将 w w w和 b b b初始在可能的最优解附近
-
步长 η \eta η如何选取?
如果选取的值比较大,那么可能短时间内能达到最优解,但是过大的 η \eta η可能让函数达不到最优解(每次刚好从最优解附近跨过去了),甚至会脱离最优解的范畴。
所以一般先取个比较大的 η \eta η,随着迭代, η \eta η满满变小,所以上述迭代可换为
w t + 1 = w t − η t ⋅ ∑ i = 1 N [ S ( w ⋅ x i + b ) − y i ] x i b t + 1 = b t − η t ⋅ ∑ i = 1 N [ S ( w ⋅ x i + b ) − y i ] \begin{aligned} w^{t+1}&=w^t-\eta_t\cdot\sum_{i=1}^N[S(w\cdot x_i+b)-y_i]x_i\\ b^{t+1}&=b^t-\eta_t\cdot\sum_{i=1}^N[S(w\cdot x_i+b)-y_i] \end{aligned} wt+1bt+1=wt−ηt⋅i=1∑N[S(w⋅xi+b)−yi]xi=bt−ηt⋅i=1∑N[S(w⋅xi+b)−yi] -
什么时候迭代停止?
停止的方式很多
-
两次迭代的目标函数差别过小停止
∣ L t ( w , b ) − L t + 1 ( w , b ) ∣ < ε |L^{t}(w,b)-L^{t+1}(w,b)|<\varepsilon ∣Lt(w,b)−Lt+1(w,b)∣<ε -
两次迭代参数的变化过小
∣ w t − w t + 1 ∣ < ε ∣ b t − b t + 1 ∣ < ε \begin{aligned} |w^{t}-w^{t+1}|&<\varepsilon\\ |b^{t}-b^{t+1}|&<\varepsilon\\ \end{aligned} ∣wt−wt+1∣∣bt−bt+1∣<ε<ε -
验证数据集
每次迭代得到的模型用验证数据集验证准确性,准确性不再上升即可停止
-
收敛法
如果算法收敛,那么迭代一定次数后会收敛到极大值
-
随机梯度下降法-梯度下降改进
观察梯度下降法的下降过程
w t + 1 = w t − η t ⋅ ∑ i = 1 N [ S ( w ⋅ x i + b ) − y i ] x i b t + 1 = b t − η t ⋅ ∑ i = 1 N [ S ( w ⋅ x i + b ) − y i ] \begin{aligned} w^{t+1}&=w^t-\eta_t\cdot\sum_{i=1}^N[S(w\cdot x_i+b)-y_i]x_i\\ b^{t+1}&=b^t-\eta_t\cdot\sum_{i=1}^N[S(w\cdot x_i+b)-y_i] \end{aligned} wt+1bt+1=wt−ηt⋅i=1∑N[S(w⋅xi+b)−yi]xi=bt−ηt⋅i=1∑N[S(w⋅xi+b)−yi]
可以发现,在 T T T次迭代中,每次迭代需要计算 N N N个样本的值才进行一次梯度更新,当 N N N比较大的时候算法比较低效
所以可以将上述迭代再进行拆分,在每次迭代 t t t中,进行 N N N次遍历,用每个样本点对参数进行梯度进行更新,这样每次迭代梯度更新 N N N次,提高了效率
w n e w = w o l d − η t ⋅ [ S ( w ⋅ x i + b ) − y i ] x i b n e w = b o l d − η t ⋅ [ S ( w ⋅ x i + b ) − y i ] \begin{aligned} w^{new}&=w^{old}-\eta_t\cdot[S(w\cdot x_i+b)-y_i]x_i\\ b^{new}&=b^{old}-\eta_t\cdot[S(w\cdot x_i+b)-y_i] \end{aligned} wnewbnew=wold−ηt⋅[S(w⋅xi+b)−yi]xi=bold−ηt⋅[S(w⋅xi+b)−yi]
但由于是使用每个样本点更新,噪声对迭代的影响会被增大,此时 η \eta η可适当减小
随机梯度下降算法求解极大似然估计值算法描述
-
**输入:**数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),..,(x_N,y_N)\} T={(x1,y1),(x2,y2),..,(xN,yN)}
-
输出: w , b w,b w,b
-
过程:
-
选取参数初始值 w 0 , b 0 w_0,b_0 w0,b0,初始步长 η 0 \eta_0 η0,最大大迭代次数 T T T
-
每次迭代,随机遍历 N N N个样本(对长度为 N N N的下标数组随机排序)
-
每次遍历使用第 i i i个样本点更新参数
w n e w = w o l d − η t ⋅ [ S ( w ⋅ x i + b ) − y i ] x i b n e w = b o l d − η t ⋅ [ S ( w ⋅ x i + b ) − y i ] \begin{aligned} w^{new}&=w^{old}-\eta_t\cdot[S(w\cdot x_i+b)-y_i]x_i\\ b^{new}&=b^{old}-\eta_t\cdot[S(w\cdot x_i+b)-y_i]\\ \end{aligned} wnewbnew=wold−ηt⋅[S(w⋅xi+b)−yi]xi=bold−ηt⋅[S(w⋅xi+b)−yi] -
回到
2.
利用收敛性停止
-
python实现
Github
import math
import random
from math import exp
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
class LR:
def __init__(self, values, labels):
values = list(values)
labels = list(labels)
# 借助一下sklearn分割数据
self.x_train, self.test_x, self.y_train, self.test_y = train_test_split(values, labels, test_size=0.3)
self.w = np.zeros(len(values[0]))
self.b = 0
self.T = 200 # 最大迭代次数
self.eta = 0.01
self.correct_rate = 0
self.train()
'''训练模型,求出参数w,b'''
def train(self):
index = list(range(len(self.x_train))) # 遍历下标
stop = False
for t in range(self.T):
if stop:
break
# 遍历下标每次打乱
random.shuffle(index)
for i in index:
self.w = self.w - np.dot(
self.eta * (self.sigmoid(np.dot(self.w, self.x_train[i]) + self.b) - self.y_train[i]),
self.x_train[i])
self.b = self.b - self.eta * (self.sigmoid(np.dot(self.w, self.x_train[i]) + self.b) - self.y_train[i])
self.correct_rate = self.cal_correct_rate()
print('模型训练结果为w={0},b={1}\n验证数据集准确率:{2}'.format(self.w, self.b, self.cal_correct_rate()))
'''
计算验证数据集的准确率
:return 验证数据集预测准确性
'''
def cal_correct_rate(self):
res_y = self.predict(self.test_x)
right_len = 0
test_len = len(self.test_x)
for i in range(test_len):
if res_y[i] == self.test_y[i]:
right_len += 1
return right_len * 1.0 / test_len
'''
预测实例类别
:param values: 实例点集合
:return: 1|0 实例点的分类
'''
def predict(self, values):
values = list(values)
res = []
for i in range(len(values)):
val = self.sigmoid((np.dot(self.w, values[i]) + self.b))
if val > 0.5:
res.append(1)
else:
res.append(0)
return res
'''sigmoid函数'''
def sigmoid(self, x):
return 1.0 / (1.0 + exp(-x))
if __name__ == '__main__':
df = pd.DataFrame(pd.read_csv('data/LR_data', encoding='utf-8'))
features = df.columns[:-1].values
data = df.values
values = data[:, :-1]
labels = data[:, -1]
lr = LR(values, labels)
数据集有点那啥所以拟合得比较好
模型训练结果为w=[-0.61107666 -2.15003769 3.3198986 1.45485017],b=-0.40464274755118707
验证数据集准确率:1.0
Process finished with exit code 0