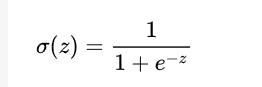Python实现逻辑斯谛回归

一 逻辑斯谛分布

我们常用的sigmoid函数其实就是逻辑斯谛分布函数 u=0,y=1 的形式

它的分布函数和密度函数的曲线如下:
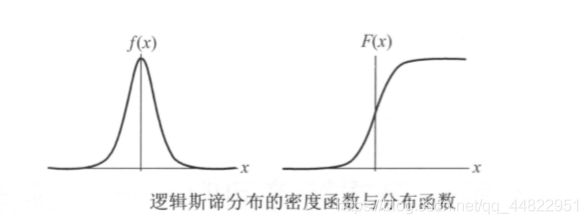根据逻辑斯谛分布函数的图像可以看出当x趋向于无穷大时,F(x) 趋向于1 当x趋向于无穷小时,F(x) 趋向于 0

二 二项逻辑斯谛回归模型

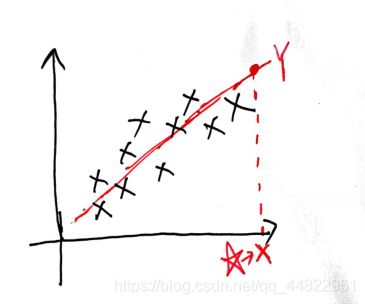
学过线性回归的朋友知道，线性回归是根据样本来学习到一条直线y=wx+b， 之后当我们输入代预测的样本X 模型就会输出一个预测的连续值Y(如下图所示)。但是如果我们想要用线性回归实现分类，似乎有点困难。分类要求输出是一个离散的类别，而不是一个连续值。
为此我们引入了一个sigmoid函数对线性回归的 y (y=wx+b) 做一个映射。

sigmoid 函数如下
它的取值在0~1之间

二项逻辑斯谛回归模型是一个二分类模型。它由条件概率分布 P(YIX) 表示,X是输入的特征向量，Y是输出的类别。

逻辑斯谛回归模型是如下的条件概率分布 令

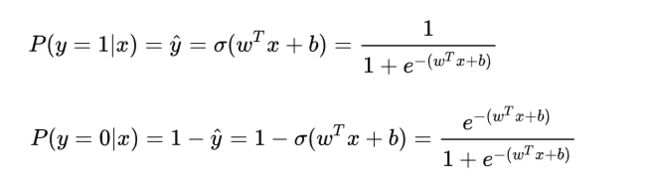
对于给定的X 比较P(Y=1|X) 与P(Y=0| X)的大小,将X分到概率值较大的那一类

三 模型损失函数

在前面我们已经得到了逻辑斯谛回归模型，但是注意到模型中还有未知的参数w,b 怎么求出w,b呢？

我们约定
所以可以得到:
则
在预测的时候 w,b 影响着 P(y|x) 的大小，我们希望P(y|x)大一点因为这样预测值就和真实值更加接近

其对数形式如下

求P(y|x)的最大值 等价于求logP(y|x)的最大值

对于单个样本将损失函数定义如下:

对整个训练集将代价函数定义为

四 梯度下降法

五 代码实现

数据来源于和鲸社区
因为数据中大多数特征值是离散的 并且是以自然语言的形式呈现的 比如
OnlineSecurity有三种取值No,Yes,No internet service,可以用LabelEncoder来编码 结果是以数字0，1，2分别代表这三种类型 对所有值是离散类型的特征都采用这种方法来处理

def datapreprocessing(data):#数据预处理
    le = LabelEncoder()
    data['gender'] = le.fit_transform(data['gender'].values)
    data['Partner'] = le.fit_transform(data['Partner'].values)
    data['Dependents'] = le.fit_transform(data['Dependents'].values)
    data['PhoneService'] = le.fit_transform(data['PhoneService'].values)
    data['MultipleLines'] = le.fit_transform(data['MultipleLines'].values)
    data['InternetService'] = le.fit_transform(data['InternetService'].values)
    data['OnlineSecurity'] = le.fit_transform(data['OnlineSecurity'].values)
    data['OnlineBackup'] = le.fit_transform(data['OnlineBackup'].values)
    data['DeviceProtection'] = le.fit_transform(data['DeviceProtection'].values)
    data['TechSupport'] = le.fit_transform(data['TechSupport'].values)
    data['StreamingTV'] = le.fit_transform(data['StreamingTV'].values)
    data['StreamingMovies'] = le.fit_transform(data['StreamingMovies'].values)
    data['Contract'] = le.fit_transform(data['Contract'].values)
    data['PaperlessBilling'] = le.fit_transform(data['PaperlessBilling'].values)
    data['PaymentMethod'] = le.fit_transform(data['PaymentMethod'].values)
    data['Churn'] = le.fit_transform(data['Churn'].values)
    print(data)
    data.to_csv('Customer-Churn.csv')#

逻辑回归模型

class LR:#逻辑回归
    def __init__(self,X_Train,Y_train,a,r):
        self.X_Train=X_Train
        self.Y_train=Y_train
        self.a=a
        self.w=self.initialization_parameters() #参数 由(w1,w2,w3 ...，b)组成
        self.r=r #迭代多少次
    def sigmoid(self,x):
        return 1 / (1 + np.exp(-x))
    def initialization_parameters(self): #初始化 w为一个n+1 维的向量 n是有n维特征
        n=self.X_Train.shape[1]
        w=np.ones((n,1))
        return w
    def cost_function(self): #损失函数
        lost=np.sum(self.Y_train*np.log2(self.sigmoid(np.dot(self.X_Train,self.w)))+(1-self.Y_train)*np.log2(1-self.sigmoid(np.dot(self.X_Train,self.w))))/self.X_Train.shape[0]
        return -lost
    def cal_dw(self): #求w的偏导数
        dw=np.dot((self.sigmoid(np.dot(self.X_Train,self.w))-self.Y_train).T,self.X_Train)/self.X_Train.shape[0]
        return dw.T
    def fit(self):
         for i in range(self.r): #循环self.r 次
             print("损失值为:")
             print(self.cost_function())
             self.w=self.w-self.a*self.cal_dw()
    def predict(self,X_Test,Y_Test):
        right = 0
        for i in range(X_Test.shape[0]):
            p=self.sigmoid(np.dot(X_Test[i],self.w))
            q=1-p
            if p>q:
                if Y_Test[i][0]==1:
                    right+=1
            else:
                if Y_Test[i][0]==0:
                    right+=1
        print("准确率为")
        print(right/X_Test.shape[0])

def read_data(filename):#将文件中的数据读出
    df = read_csv(filename)
    return df
def prepare_data(df):  # 数据预处理
    ndarray_data = df.values
    X = df.iloc[:, 2:21]  # 数据切片
    Y = df.iloc[:, 21]
    print(X)
   # 特征值标准化\n"
    minmax_scale = preprocessing.MinMaxScaler(feature_range=(0, 1))
    X = minmax_scale.fit_transform(X)
   # Y = Y.replace(0, -1)
    return X, Y

模型调用过程

df=read_data("Customer-Churn.csv")#读数据
df['TotalCharges'] = df['TotalCharges'].replace(" ", "0")#TotalCharges中有空格
df['TotalCharges'] = pd.to_numeric(df['TotalCharges'])
TotalCharges = []
for i in range(df.shape[0]):
    TotalCharges.append(float(df.loc[i, 'TotalCharges']))  # 将字符串数据转化为浮点型加入到数组之中
avg=np.var(TotalCharges)
df['TotalCharges'] = df['TotalCharges'].replace(0, avg)#用均值填充缺失值
print(df.shape)#(7043, 21)
#print(df.dtypes)#查看各列数据的数据类型
X,Y=prepare_data(df)
train_size = int(len(X) * 0.8)#划分训练集与测试集
X_train = np.array(X[:train_size])
print(X_train.shape)
Y_train=np.array(Y[:train_size])
Y_train.resize([Y_train.shape[0],1])
X_test = np.array(X[train_size:])
Y_test =np.array( Y[train_size:])
Y_test.resize([Y_test.shape[0],1])
a = np.ones(X_train.shape[0])
b = np.ones(X_test.shape[0])
X_train=np.insert(X_train, 19, values=a, axis=1)
X_test=np.insert(X_test, 19, values=b, axis=1)
model=LR(X_train,Y_train,0.05,20000)
model.fit()
model.predict(X_test,Y_test)