对RNN、LSTM、GRU的理解
GRU结构
GRU是LSTM的简化结构,而LSTM是RNN的优化结构。所以要理解GRU的结构,首先要先理解它的两个祖先:RNN和LSTM。
- RNN:
RNN的结构十分简单,就是将网络的输出保存在一个记忆单元中,这个记忆单元的输出经过权重参数调整后和下一次的输入一起进入神经网络中。区别于传统DPN和CNN,由于RNN除了第一轮输入输出以外,每轮输入输出都保有上一轮的信息(上一轮输出经过参数调整后又变为本轮的输入),使其输出结果与输入信息顺序有关。因此可以处理序列信息数据,如由不同字母组成的单词,短语等
公式:图1 RNN结构
Ot=g(V*St)
St=f(U*Xt+W*St-1)
其中:
Ot为t时刻输出数值
St为t时刻记忆体数值
Xt为t时刻输入数值
U为输入权重
V为输出权重
W为上一轮输出(St-1)重新作为输入的权重
g()为输出激活函数,一般为tanh函数。
f()为输入激活函数,一般为tan函数。
LSTM:通过观察sigmoid图像就会发现,整个图像在x负无穷到-2.5这段区间,以及正2.5到正无穷这段区间你内函数的梯度都接近于0,而在负2.5到正2.5这段区间函数图像都接近线性(接近但仍小于等于1),所以tanh图像整体都恒小于1.这就引来一个很严重的问题:梯度消失。
RNN结构中St由St-1与Xt都要经过激活函数tanh(St=f(U*Xt+W*St-1),其中f就是激活函数tanh)。而随着时间步逐渐增大,较早的记忆体数值S1、S2...等数据会经过许多轮tanh函数处理,然而因为tanh函数梯度无论如何取值都小于等于1,任何一个数收到小于1的数连乘都会逐渐变小乃至接近0.(如100*0.9*0.9*0.9....*0.9=0)。因此较早的记忆体数值S1、S2...等数据会在经过多轮tanh后逐渐减弱到消失,造成RNN网络“长期记忆丢失”,“只记得短期记忆”,是长期记忆失去对后面的输出的影响。
解决这件事的办法并不是将tanh函数更换成梯度大于1的激活函数那么简单,因为激活函数梯度小于1固然可以通过增大梯度解决,但把激活函数梯度调整到大于1又会引发另外的一个问题:梯度爆炸。
因为任何一个数在连乘大于1的数后会都会逐渐变大,随着时间步增加,早期记忆体内的数值会逐渐增大到天文数字,会导致越长期记忆对后续输出的影响越大,而短期记忆反而没那么大影响。与梯度消失的效果相反。
无论是梯度消失和梯度爆炸都是长短期作用失衡造成的,那能不能设计一段既有梯度大于1区间又有梯度小于1区间的激活函数呢?这个想法固然可以。但这样的激活函数却无法判断那段长期记忆是重要的还是不重要的,那段短期记忆是重要的还是不重要的。可能会把重要的记忆在梯度小于1的区域连乘失去,不重要的冗余数据保存起来等等问题。
为解决RNN长期记忆丢失的问题,LSTM出现了。LSTM(Long Short Term Mermory network)是一种特殊的RNNs,可以很好地解决长时依赖问题。那么它与常规神经网络有什么不同?
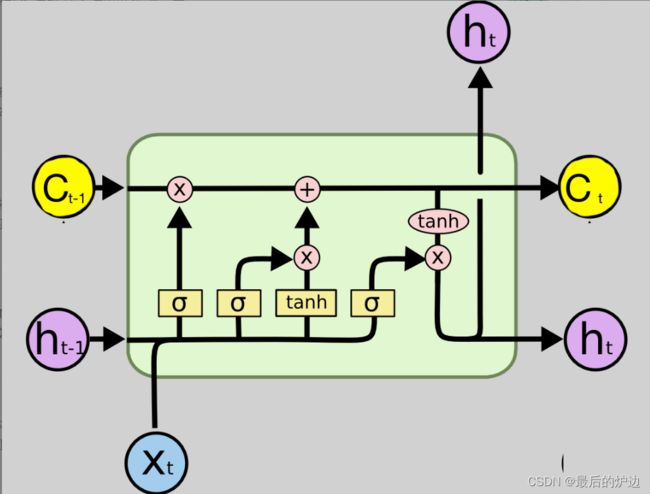
LSTM主要由遗忘门、输入门、输出门与记忆单元组成。如下图所示
图2 LSTM结构
首先先指明图中信息
Xt为t时刻外部输入信息
St为t时刻输出结果信息
St-1为t-1时刻输出结果信息
Ct为t时刻LSTM细胞态信息
Ct-1为t-1时刻LSTM细胞态信息
ft为t时刻遗忘门状态
It为t时刻输入门状态
~Ct为t时刻候选细胞态信息(相当于神经细胞固有属性,用于存储长期记忆)
1.LSTM的第一步由遗忘门控制t-1时刻的细胞态信息Ct-1能保留多少进入t时刻的细胞态信息Ct,它会通过上一轮输出ht-1和当前输入xt经过权重遗忘门权重参数Wf后加上偏置项Bf(偏置项的作用是加快反向传播时的拟合速度)sigmoid函数(图像由图3.2.5所示)产生零到一的数值ft.(用来模拟电路中的门:0代表完全关闭,1代表完全打开)。
公式为
ft=sigmoid(Wf*[St-1,xt]+bf)
这里遗忘门的作用是将没有用的t-1时刻细胞态信息过滤掉,将剩余信息保留到t时刻。
LSTM的第二步用生成t时刻候选细胞态~Ct和输入门状态it,~Ct是由t时刻外部输入信息Xt与t-1时刻输出结果信息St-1通过候选细胞态权重Wc相乘并与候选细胞态偏置值bc相加后的中间值再经过tanh函数得到的候选细胞态值。而it是由t时刻外部输入信息Xt与t-1时刻输出结果信息St-1通过候选细胞态权重Wc相乘并与候选细胞态偏置值bc相加后的中间值再经过sigmoid函数得到的输入门状态。
公式为
~Ct=tanh(Wc*[St-1,xt]+bc)
it=sigmoid(Wi*[St-1,xt]+bi)
这里~Ct候选是根据当前信息(St-1和Xt)生产用来预备进入细胞态(长期记忆)的信息。而输入门状态it取值也为0~1,用于根据当前信息(St-1和Xt)的重要程度来决定由当前信息(St-1和Xt)生产的选定候选细胞态~Ct能有多少能进入真正的细胞态Ct,以把重要的信息作为长期记忆来影响未来结果。
LSTM的第三步先对“老的”细胞态(t-1时刻)Ct-1经过遗忘门“忘掉”(过滤掉)过时的,无关紧要的信息。再将未来可能会有用的候选信息细胞态信息~Ct经过输入门it相乘后得到真正有用的信息并入到已有的细胞态当中,最终得到新的(t时刻)的细胞态信息Ct。
公式为
Ct=ft*Ct-1+it*~Ct
Ct信息可以类比为英语词汇量,是日积月累的结果,会随着时间推移逐渐遗忘掉不常用的词汇并随着学习和运用保留新的词汇。本有的词汇量的大小Ct和现在看到的本段英语句子的各个组成单词Xt和上一句英语句子翻译结果St-1决定着在本段英语句子的结果St。
LSTM的第四步输出t时刻结果信息St,首先先由St-1和Xt经过输出权重Wo后加上输出偏置值bo后,生成输出门状态Ot。再由Ct经过tanh函数压缩信息后经过输出门状态Ot得到t时刻输出结果St。
公式为
Ot=sigmoid(Wo[St-1,Xt]+bo)
St=Ot*tanh(Ct)
联系第三部末尾的举例,这里输出门Ot可以理解为由前句翻译结果St-1和本句的各个单词Xt组成的语境(sigmoid(Wo[St-1,Xt]+bo)),根据语境Ot把自己已掌握的单词Ct通过简练地(tanh函数)表达(过程为Ot*tanh(Ct))成本句的翻译结果St。
图3 LSTM结构
图4 Sigmoid函数图像(与tanh函数类似)
回顾一下LSTM的模型,它实现了三个门计算,即遗忘门、输入门和输出门,但是由于LSTM的重复网络模块的结构很复杂,中间参数杂多,在实际训练数据时比较耗时。为了解决这一问题,GRU模型诞生了。
GRU则是LSTM的一个变体,相比LSTM,使用GRU能够达到相当的效果,并且相比之下更容易进行训练,能够很大程度上提高训练效率,因此很多时候会更倾向于使用GRU。
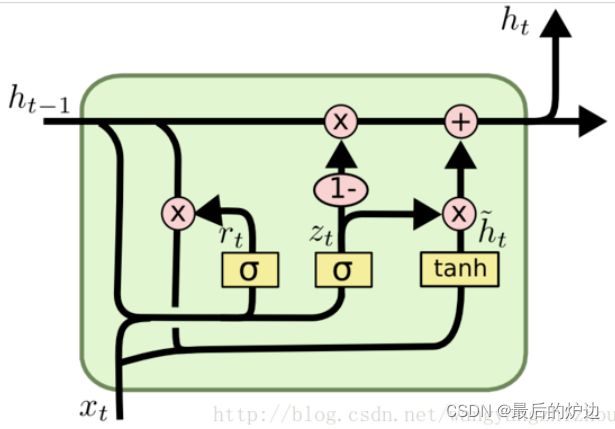
GRU模型如图3.2.6所示,它只有两个门了,分别为更新门和重置门,即图中的zt和rt。
首先先指明图中信息
ht为t时刻隐藏状态变量
ht-1为t-1时刻隐藏状态变量
~ht为t时刻候选隐藏状态变量
xt为t时刻的外部输入信息
rt为t时刻重置门状态
zt为t时刻更新门状态
1.GRU的第一步是将上一轮的隐藏状态变量ht-1和本轮的输入xt信息,通过乘以重置门权重wr并通过sigmoid函数来获取重置门状态rt。通过乘以更新门权重获得更新门权重并通过sigmoid函数来获得更新门状态zt。
公式为
rt=sigmoid(wr*[xt,ht-1])
zt=sigmoid(wz*[xt,ht-1])
其中rt可以比喻为线索状态,用于往后将已掌握的信息推理成更新的信息~ht-1。而zt是根据现有xt和ht-1的重要程度,决定获得的后面信息遗忘和和记忆。
2.GRU的第二步是在得到重置门状态后,将ht-1经过重置门状态rt相乘得到中间变量~ht-1,再将中间变量~ht-1和外部输入变量xt拼接后经过tanh函数得到本次候选隐藏状态变量~ht。
公式为
~ht-1=ht-1*rt
~ht=tanh(wh*[xt,~ht-1])
其中~ht-1=ht-1*rt可以比喻为从原有的信息ht-1根据线索程度rt推到出新的信息~ht-1(根据线索推导的信息即包括有用信息又包括无用信息)。~ht是根据以推到的信息~ht-1与现有信息xt整合并简练化(tanh函数)得到的本次候选隐藏状态变量。
3.GRU的第三步,也是最关键的一步,“更新记忆”,在这一步要同时经历遗忘和记忆两个步骤。
公式为
ht=(1-zt)*ht-1+zt*~ht
其中zt和(1-zt)作为记忆状态和遗忘状态,(1-zt)*ht-1表示对原有的信息选择性遗忘,遗忘掉不重要的信息。Zt*~ht表示对候选信息选择性记忆,记忆有用的信息。更新门状态越接近1,记忆的信息就会越多,更新门越接近0,遗忘的东西就会越多。
图5 GRU结构
综上所述,可以很明显看出,GRU比LSTM复杂程度降低了不少,而且不仅去掉了了每一步公式的偏置值b,也将LSTM的细胞态(长期记忆)Ct和上轮输出St-1两个变量整合成h,还将LSTM的遗忘和输入门两个门整合成了更新门单独一个门。大大简化了LSTM的计算量,而且大体保留了LSTM的功能。使其既能不大影响LSTM准确度的同时,还对LSTM进行了精简。这就是GRU流行起来的主要原因。
3.4预测模型
为表示GRU模型对编号为000001的股票预测的准确性,本文用编号为000001,股票从2012年2月1日开始到2022年1月24日结束的2426天作为数据集,并把数据集拆分为前2126天作为训练集训练模型,后300天作为测试集测试模型。
样本方差公式作为损失函数,如图3.3.1所示,其中蓝色曲线代表训练过程中预测的结果与标签的误差函数,橙色曲线代表样本自身的误差函数,竖坐标代表样本方差大小,横坐标代表训练轮数。可以看到,在第一轮到第二轮训练时误差函数就快速下降然后趋于平缓,第二轮到第20轮之间训练误差以微小的下降趋势逼近真实的样本误差曲线,20轮以后蓝色曲线已保持稳定的距离,并且与真实样本误差曲线距离很小。
图6 GRU对000001号股票预测的样本方差和实际样本方差
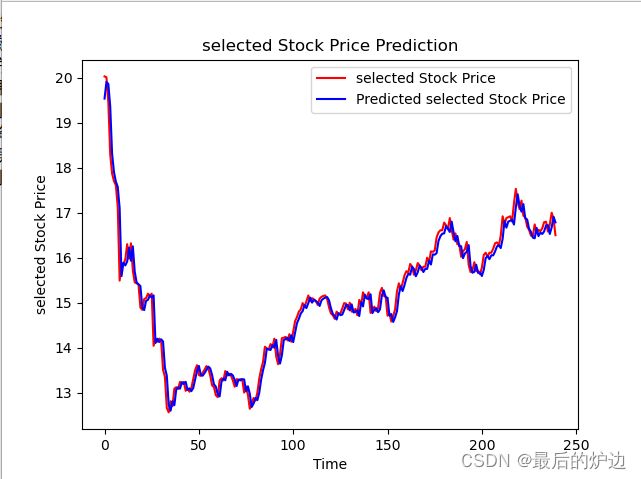
五十轮训练后GRU模型对000001号股票的股价走势的预测结果如图3.3.2所示,其中陈设为真实股票走势。紫色为预测股票走势,竖坐标表示股票股价,横坐标表示时间推移。可以很清楚看到整体预测走势和实际走势高度吻合。
图7 GRU对000001号股票预测股价走势和实际走势
要在变化莫测的实际股票市场中表出更加优异的效果,可以添加成交量,换手率等参数,并加入attention机制。本文因为篇幅有限,不予讨论。
综上可知GRU算法对股价模型拥有很好的预测能力,而且只需要较短的训练时间就可以达到实际运用的效果。