统计学习方法读书笔记15-逻辑斯蒂回归习题
文章目录
-
-
- 1.课后习题
- 2.视频课后习题
-
1.课后习题
import numpy as np
import time
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from pylab import mpl
# 图像显示中文
mpl.rcParams['font.sans-serif'] = ['Microsoft YaHei']
class LogisticRegression:
def __init__(self, learn_rate=0.1, max_iter=10000, tol=1e-2):
self.learn_rate = learn_rate # 学习率
self.max_iter = max_iter # 迭代次数
self.tol = tol # 迭代停止阈值
self.w = None # 权重
def preprocessing(self, X):
"""将原始X末尾加上一列，该列数值全部为1"""
row = X.shape[0]
y = np.ones(row).reshape(row, 1)
X_prepro = np.hstack((X, y))
return X_prepro
def sigmod(self, x):
return 1 / (1 + np.exp(-x))
def fit(self, X_train, y_train):
X = self.preprocessing(X_train)
y = y_train.T
# 初始化权重w
self.w = np.array([[0] * X.shape[1]], dtype=np.float)
k = 0
for loop in range(self.max_iter):
# 计算梯度
z = np.dot(X, self.w.T)
grad = X * (y - self.sigmod(z))
grad = grad.sum(axis=0)
# 利用梯度的绝对值作为迭代中止的条件
if (np.abs(grad) <= self.tol).all():
break
else:
# 更新权重w 梯度上升——求极大值
self.w += self.learn_rate * grad
k += 1
print("迭代次数：{}次".format(k))
print("最终梯度：{}".format(grad))
print("最终权重：{}".format(self.w[0]))
def predict(self, x):
p = self.sigmod(np.dot(self.preprocessing(x), self.w.T))
print("Y=1的概率被估计为：{:.2%}".format(p[0][0])) # 调用score时，注释掉
p[np.where(p > 0.5)] = 1
p[np.where(p < 0.5)] = 0
return p
def score(self, X, y):
y_c = self.predict(X)
error_rate = np.sum(np.abs(y_c - y.T)) / y_c.shape[0]
return 1 - error_rate
def draw(self, X, y):
# 分离正负实例点
y = y[0]
X_po = X[np.where(y == 1)]
X_ne = X[np.where(y == 0)]
# 绘制数据集散点图
ax = plt.axes(projection='3d')
x_1 = X_po[0, :]
y_1 = X_po[1, :]
z_1 = X_po[2, :]
x_2 = X_ne[0, :]
y_2 = X_ne[1, :]
z_2 = X_ne[2, :]
ax.scatter(x_1, y_1, z_1, c="r", label="正实例")
ax.scatter(x_2, y_2, z_2, c="b", label="负实例")
ax.legend(loc='best')
# 绘制p=0.5的区分平面
x = np.linspace(-3, 3, 3)
y = np.linspace(-3, 3, 3)
x_3, y_3 = np.meshgrid(x, y)
a, b, c, d = self.w[0]
z_3 = -(a * x_3 + b * y_3 + d) / c
ax.plot_surface(x_3, y_3, z_3, alpha=0.5) # 调节透明度
plt.show()
# 训练数据集
X_train = np.array([[3, 3, 3], [4, 3, 2], [2, 1, 2], [1, 1, 1], [-1, 0, 1], [2, -2, 1]])
y_train = np.array([[1, 1, 1, 0, 0, 0]])
# 构建实例，进行训练
clf = LogisticRegression()
clf.fit(X_train, y_train)
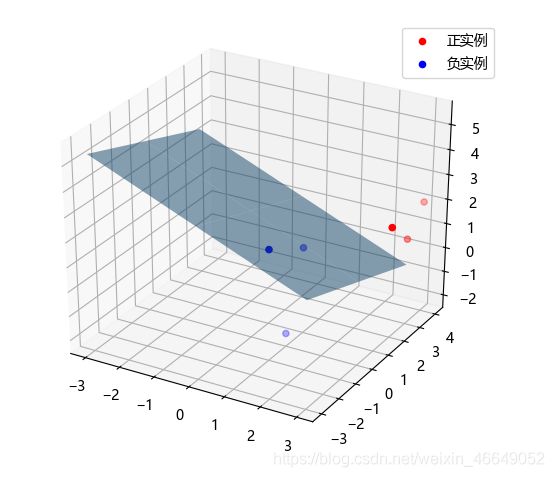
clf.draw(X_train, y_train)
迭代次数：3232次
最终梯度：[ 0.00144779 0.00046133 0.00490279 -0.00999848]
最终权重：[ 2.96908597 1.60115396 5.04477438 -13.43744079]
链接3
2.视频课后习题
"""逻辑斯蒂回归算法实现-使用梯度下降"""
# 全梯度下降法
import numpy as np
import time
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
# mpl.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
class LogisticRegression:
def __init__(self, learn_rate=0.01, max_iter=10000, tol=1e-2):
self.learn_rate = learn_rate # 学习率
self.max_iter = max_iter # 迭代次数
self.tol = tol # 迭代停止阈值
self.w = None # 权重
def preprocessing(self, X):
"""将原始X末尾加上一列，该列数值全部为1"""
row = X.shape[0]
y = np.ones(row).reshape(row, 1)
X_prepro = np.hstack((X, y))
return X_prepro
def sigmod(self, x):
return 1 / (1 + np.exp(-x))
def fit(self, X_train, y_train):
X = self.preprocessing(X_train)
y = y_train.T
# 初始化权重w
self.w = np.array([[0] * X.shape[1]], dtype=np.float)
k = 0
for loop in range(self.max_iter):
# 计算梯度
z = np.dot(X, self.w.T)
grad = X * (y - self.sigmod(z))
grad = grad.sum(axis=0)
# 利用梯度的绝对值作为迭代中止的条件
if (np.abs(grad) <= self.tol).all():
break
else:
# 更新权重w 梯度上升——求极大值
self.w += self.learn_rate * grad
k += 1
print("迭代次数：{}次".format(k))
print("最终梯度：{}".format(grad))
print("最终权重：{}".format(self.w[0]))
def predict(self, x):
p = self.sigmod(np.dot(self.preprocessing(x), self.w.T))
print("Y=1的概率被估计为：{:.2%}".format(p[0][0])) # 调用score时，注释掉
p[np.where(p > 0.5)] = 1
p[np.where(p < 0.5)] = 0
return p
def score(self, X, y):
y_c = self.predict(X)
error_rate = np.sum(np.abs(y_c - y.T)) / y_c.shape[0]
return 1 - error_rate
def draw(self, X, y):
# 分离正负实例点
y = y[0]
X_po = X[np.where(y == 1)]
X_ne = X[np.where(y == 0)]
# 绘制数据集散点图
ax = plt.axes(projection='3d')
x_1 = X_po[0, :]
y_1 = X_po[1, :]
z_1 = X_po[2, :]
x_2 = X_ne[0, :]
y_2 = X_ne[1, :]
z_2 = X_ne[2, :]
ax.scatter(x_1, y_1, z_1, c="r", label="正实例")
ax.scatter(x_2, y_2, z_2, c="b", label="负实例")
ax.legend(loc='best')
# 绘制p=0.5的区分平面
x = np.linspace(-3, 3, 3)
y = np.linspace(-3, 3, 3)
x_3, y_3 = np.meshgrid(x, y)
a, b, c, d = self.w[0]
z_3 = -(a * x_3 + b * y_3 + d) / c
ax.plot_surface(x_3, y_3, z_3, alpha=0.5) # 调节透明度
plt.show()
def main():
star = time.time()
# 训练数据集
X_train = np.array([[3, 3, 3], [4, 3, 2], [2, 1, 2], [1, 1, 1], [-1, 0, 1], [2, -2, 1]])
y_train = np.array([[1, 1, 1, 0, 0, 0]])
# 构建实例，进行训练
clf = LogisticRegression()
clf.fit(X_train, y_train)
# 预测新数据
X_new = np.array([[1, 2, -2]])
y_predict = clf.predict(X_new)
print("{}被分类为：{}".format(X_new[0], y_predict[0]))
clf.draw(X_train, y_train)
# 利用已有数据对训练模型进行评价
X_test=X_train
y_test=y_train
correct_rate=clf.score(X_test,y_test)
print("共测试{}组数据，正确率：{:.2%}".format(X_test.shape[0],correct_rate))
end = time.time()
print("用时：{:.3f}s".format(end - star))
if __name__ == "__main__":
main()
迭代次数：10000次
最终梯度：[ 0.00483138 0.00138275 0.01561255 -0.03217626]
最终权重：[ 2.40550339 1.42893511 3.19459105 -9.63604478]
Y=1的概率被估计为：0.00%
[ 1 2 -2]被分类为：[0.]
Y=1的概率被估计为：100.00%
共测试6组数据，正确率：100.00%
用时：0.324s
"""逻辑斯蒂回归算法实现-使用随机梯度下降"""
# 随机梯度下降法
import numpy as np
import time
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
class LogisticRegression:
def __init__(self, learn_rate=0.01, max_iter=10000, tol=1e-3):
self.learn_rate = learn_rate # 学习率
self.max_iter = max_iter # 迭代次数
self.tol = tol # 迭代停止阈值
self.w = None # 权重
def preprocessing(self, X):
"""将原始X末尾加上一列，该列数值全部为1"""
row = X.shape[0]
y = np.ones(row).reshape(row, 1)
X_prepro = np.hstack((X, y))
return X_prepro
def sigmod(self, x):
return 1 / (1 + np.exp(-x))
def fit(self, X_train, y_train):
X = self.preprocessing(X_train)
y = y_train.T
# 初始化权重w
self.w = np.array([[0] * X.shape[1]], dtype=np.float)
i = 0
k = 0
for loop in range(self.max_iter):
# 计算梯度
z = np.dot(X[i], self.w.T)
grad = X[i] * (y[i] - self.sigmod(z))
# 利用梯度的绝对值作为迭代中止的条件
if (np.abs(grad) <= self.tol).all():
break
else:
# 更新权重w 梯度上升——求极大值
self.w += self.learn_rate * grad
k += 1
# 由于迭代轮数可能超过数据量，所以需要取余
i = (i + 1) % X.shape[0]
print("迭代次数：{}次".format(k))
print("最终梯度：{}".format(grad))
print("最终权重：{}".format(self.w[0]))
def predict(self, x):
p = self.sigmod(np.dot(self.preprocessing(x), self.w.T))
print("Y=1的概率被估计为：{:.2%}".format(p[0][0])) # 调用score时，注释掉
p[np.where(p > 0.5)] = 1
p[np.where(p < 0.5)] = 0
print('p=', p)
return p
def score(self, X, y):
y_c = self.predict(X)
error_rate = np.sum(np.abs(y_c - y.T)) / y_c.shape[0]
return 1 - error_rate
def draw(self, X, y):
# 分离正负实例点
y = y[0]
X_po = X[np.where(y == 1)]
X_ne = X[np.where(y == 0)]
# 绘制数据集散点图
ax = plt.axes(projection='3d')
x_1 = X_po[0, :]
y_1 = X_po[1, :]
z_1 = X_po[2, :]
x_2 = X_ne[0, :]
y_2 = X_ne[1, :]
z_2 = X_ne[2, :]
ax.scatter(x_1, y_1, z_1, c="r", label="正实例")
ax.scatter(x_2, y_2, z_2, c="b", label="负实例")
ax.legend(loc='best')
# 绘制p=0.5的区分平面
x = np.linspace(-3, 3, 3)
y = np.linspace(-3, 3, 3)
x_3, y_3 = np.meshgrid(x, y)
a, b, c, d = self.w[0]
z_3 = -(a * x_3 + b * y_3 + d) / c
ax.plot_surface(x_3, y_3, z_3, alpha=0.5) # 调节透明度
plt.show()
def main():
star = time.time()
# 训练数据集
X_train = np.array([[3, 3, 3], [4, 3, 2], [2, 1, 2], [1, 1, 1], [-1, 0, 1], [2, -2, 1]])
y_train = np.array([[1, 1, 1, 0, 0, 0]])
# 构建实例，进行训练
clf = LogisticRegression()
clf.fit(X_train, y_train)
# 预测新数据
X_new = np.array([[1, 2, -2],[4, 3, 2]])
y_predict = clf.predict(X_new)
print("{}被分类为：{}".format(X_new[0], y_predict[0]))
clf.draw(X_train, y_train)
# 利用已有数据对训练模型进行评价
# X_test=X_train
# y_test=y_train
# correct_rate=clf.score(X_test,y_test)
# print("共测试{}组数据，正确率：{:.2%}".format(X_test.shape[0],correct_rate))
end = time.time()
print("用时：{:.3f}s".format(end - star))
if __name__ == "__main__":
main()
迭代次数：10000次
最终梯度：[-0.29285292 -0.29285292 -0.29285292 -0.29285292]
最终权重：[ 1.53586681 1.23393345 0.75978189 -4.42286443]
Y=1的概率被估计为：12.58%
p= [[0.]
[1.]]
[ 1 2 -2]被分类为：[0.]
用时：0.271s
"""逻辑斯蒂回归算法实现-调用sklearn模块"""
from sklearn.linear_model import LogisticRegression
import numpy as np
def main():
# 训练数据集
X_train=np.array([[3,3,3],[4,3,2],[2,1,2],[1,1,1],[-1,0,1],[2,-2,1]])
y_train=np.array([1,1,1,0,0,0])
# 选择不同solver,构建实例，进行训练、测试
methodes=["liblinear","newton-cg","lbfgs","sag","saga"]
res=[]
X_new = np.array([[1, 2, -2]])
for method in methodes:
clf=LogisticRegression(solver=method,intercept_scaling=2,max_iter=1000)
clf.fit(X_train,y_train)
# 预测新数据
y_predict=clf.predict(X_new)
#利用已有数据对训练模型进行评价
X_test=X_train
y_test=y_train
correct_rate=clf.score(X_test,y_test)
res.append((y_predict,correct_rate))
# 格式化输出
methodes=["liblinear","newton-cg","lbfgs ","sag ","saga "]
# ''.join()-‘delimiter’.join(seq)表示将序列中的元素以指定的字符连接生成一个新的字符串。
# seq表示要连接的元素序列、字符串、元组、字典
print("solver选择： {}".format(" ".join(method for method in methodes)))
print("{}被分类为： {}".format(X_new[0]," ".join(str(re[0]) for re in res)))
# round() 方法返回浮点数x的四舍五入值。
print("测试{}组数据，正确率： {}".format(X_train.shape[0]," ".join(str(round(re[1],1)) for re in res)))
if __name__=="__main__":
main()
solver选择： liblinear newton-cg lbfgs sag saga
[ 1 2 -2]被分类为： [0] [0] [0] [0] [0]
测试6组数据，正确率： 1.0 1.0 1.0 1.0 1.0