基于BP人工神经网络的数字字符识别及MATLAB实现

应用背景：在模式识别中，有一种高实用性的分类方法，就是人工神经网络，它被成功应用于智能机器人、自动控制、语音识别、预测估计、生物、医学、经济等领域，解决了许多其他分类方法难以解决的实际问题。这得益于神经网络的模型比较多，可针对不同的问题使用相应的神经网络模型，这里使用BP神经网络解决手写的数字字符识别问题。

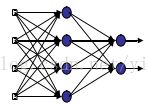
BP神经网络基本原理概述：这种网络模型利用误差反向传播训练算法模型，能够很好地解决多层网络中隐含层神经元连接权值系数的学习问题，它的特点是信号前向传播、误差反向传播，简称BP（Back  Propagation）神经网络。BP学习算法的基本原理是梯度最快下降法，即通过调整权值使网络总误差最小，在信号前向传播阶段，输入信号经输入层处理再经隐含层处理最后传向输出层处理；在误差反向传播阶段，将输出层输出的信号值与期望输出信号值比较得到误差，若误差较大则把误差信号传回隐含层直至输入层，在各层神经元中使用误差信号修改权值系数，之后进入下一轮迭代，如此循环直至误差最小，实际输出信号值接近期望输出信号值。下图为三层BP神经网络模型：

                                                                                                          

它包括输入层、1层隐含层、输出层，是一种最简单的BP神经网络模型。用这个模型解决手写的数字字符识别问题的MATLAB代码如下：

%三层BP神经网络应用于字符识别
clc;  
clear all;  
close all;  
Files= dir('C:\Program Files\MATLAB\R2013a\bin\work\CNN数字字符识别1\data');  
LengthFiles= length(Files);  
%========读取存在data文件夹下0-10个文件的全部图片========%  
for i = 3:LengthFiles;     
    if strcmp(Files(i).name,'.')||strcmp(Files(i).name,'..')  
    else  
       rootpath=strcat('C:\Program Files\MATLAB\R2013a\bin\work\CNN数字字符识别1\data','\',Files(i).name);
       filelist=dir(rootpath);  
       [filenum,temp]=size(filelist);  
       count=0;  
       imglist=cell(0);  
       for j=1:filenum      
           if strcmp(filelist(j).name,'.')|| strcmp(filelist(j).name,'..')||strcmp(filelist(j).name,'Desktop_1.ini')||strcmp(filelist(j).name,'Desktop_2.ini')         
           else  
              count=count+1;  
            imglist{count}=imread(strcat(rootpath,'/',filelist(j).name));  
           end  
       end
       number{i-2}=imglist;
    end   
end  
charvec1=zeros(35,5000);  
%========对读取的图片预处理（二值化-裁剪-特征提取）========%  
 for i=1:10  
     for j=1:500  
        I1=number{1,i}{1,j}; %第i个文件夹的第j张图 
        img_bw = im2bw(I1,graythresh(I1));  %灰度图转二值图
        bw_7050=imresize(img_bw,[70,50]);
        %提取特征统计每个小区域中图像象素所占百分比作为特征数据
        for cnt=1:7
            for cnt2=1:5
              Atemp=sum(bw_7050(((cnt*10-9):(cnt*10)),((cnt2*10-9):(cnt2*10))));%10*10box对矩阵所有元素求和，共100个像素
              lett((cnt-1)*5+cnt2)=sum(Atemp);%按行求和
            end
        end
        lett=((100-lett)/100);
        lett=lett';
        charvec1(:,(i-1)*500+j)=lett;  
     end  
 end  
 %每个样本对应的类标签向量
label=[zeros(1,500),zeros(1,500)+1,...  
   zeros(1,500)+2,zeros(1,500)+3,zeros(1,500)+4,zeros(1,500)+5,zeros(1,500)+6,zeros(1,500)+7,zeros(1,500)+8,zeros(1,500)+9];  
charvec1(36,:)=label;  
%输入输出数据  
input=charvec1(1:35,:);  
output1=charvec1(36,:); %目标输出类标签    
%把输出从1维变成10维  
for i=1:5000  
    switch output1(i)  
        case 0  
            output(:,i)=[1 0 0 0 0 0 0 0 0 0]';  
        case 1  
            output(:,i)=[0 1 0 0 0 0 0 0 0 0]';  
        case 2  
            output(:,i)=[0 0 1 0 0 0 0 0 0 0]';  
        case 3  
            output(:,i)=[0 0 0 1 0 0 0 0 0 0]';  
        case 4  
            output(:,i)=[0 0 0 0 1 0 0 0 0 0]';  
        case 5  
            output(:,i)=[0 0 0 0 0 1 0 0 0 0]';  
        case 6  
            output(:,i)=[0 0 0 0 0 0 1 0 0 0]';  
        case 7  
            output(:,i)=[0 0 0 0 0 0 0 1 0 0]';  
        case 8  
            output(:,i)=[0 0 0 0 0 0 0 0 1 0]';  
        case 9  
            output(:,i)=[0 0 0 0 0 0 0 0 0 1]';  
    end  
end    
 %=========BP神经网络创建，训练和测试========%   
%% 网络结构初始化  
innum=35;  %输入层的输入维数
midnum=80;  %中间隐含层的维数
outnum=10;  %输出层的输出维数 
%提取450个样本为训练样本
input_train=input(:,1:450); 
T=output(:,1:450); 
%权值初始化  
Wij=rands(midnum,innum);%输入到隐含层的权重向量  
b1=rands(midnum,1);  %偏值或阈值
Wki=rands(outnum,midnum);%隐含层到输出层的权重向量  
b2=rands(outnum,1); %偏值或阈值 
Ir=0.05;err_goal=0.001;  %Ir为学习速率，err_goal为期望误差最小值
max_epoch=1000;a=0.9;  %训练的最大次数，a为惯性系数  
Oi=0;Ok=0;  %初始化隐含层的输出值为0；初始化输出层的输出值为0
[M,N]=size(input_train);
Wij0=zeros(midnum,M);Wki0=zeros(outnum,midnum);
%第一阶段，模型训练期：根据加权系数Wij，Wki，对给定的样本计算输出
for epoch=1:max_epoch
    %计算隐含层各神经元节点输出
    for i=1:N
        NETi(:,i)=Wij*input_train(:,i)+b1; 
    end
    for j=1:N
        for i=1:midnum
                 Oi(i,j)=1/(1+exp(double(-NETi(i,j))));%激励函数
        end
    end 
    %计算输出层各神经元节点输出
    for i=1:N
         NETk(:,i)=Wki*Oi(:,i)+b2;
    end
    for i=1:N
        for k=1:outnum
                 Ok(k,i)=1/(1+exp(double(-NETk(k,i))));%激励函数
        end
    end
    %计算误差函数：方差    
    E=( (T-Ok)' * (T-Ok) );
    err=abs(E)>err_goal;
    if sum(sum(err))==0
       break;
    end
    %调整输出层加权系数，引入惯性项即最近一次历史权值，也就是上一次迭代的权值
    delta_k=Ok.*(1-Ok).*(T-Ok);
    W=Wki;
    Wki=Wki + Ir*delta_k*Oi' + a*(Wki-Wki0);
    Wki0=W;
    %调整隐含层加权系数，引入惯性项
    delta_i=Oi.*(1-Oi).*(delta_k' * Wki)';
    W=Wij;
    Wij=Wij+Ir*delta_i* input_train'+ a*(Wij-Wij0);
    Wij0=W;
end
epoch   %显示训练次数
%第二阶段，测试期：根据训练好的加权系数Wij，Wki，对给定的输入计算输出
input_test=input(:,451);%给定输入
X1=input_test;
output_test=output(:,451);
[M,N]=size(X1);
Oi=0;Ok=0;
%计算隐含层各神经元节点输出
for i=1:N
	 NETi1(:,i)=Wij*X1(:,i)+b1; 
end
for j=1:N
        for i=1:midnum           
            Oi(i,j)=1/(1+exp(double(-NETi1(i,j))));%激励函数
        end
end
%计算输出层各神经元节点输出
for i=1:N
    NETk1(:,i)=Wki*Oi(:,i)+b2;  
end
for i=1:N
        for k=1:outnum
            Ok(k,i)=1/(1+exp(double(-NETk1(k,i))));%激励函数
        end
end
output_test'    %显示网络输出层的期望输出
Ok'   %显示网络输出层的实际输出

程序中使用450张写了数字“0”的图片作为训练样本以及1张写了数字“0”的图片作为测试样本，运行结果如下图

从运行结果看，模型训练了2次就成功，识别率高，为0.99。