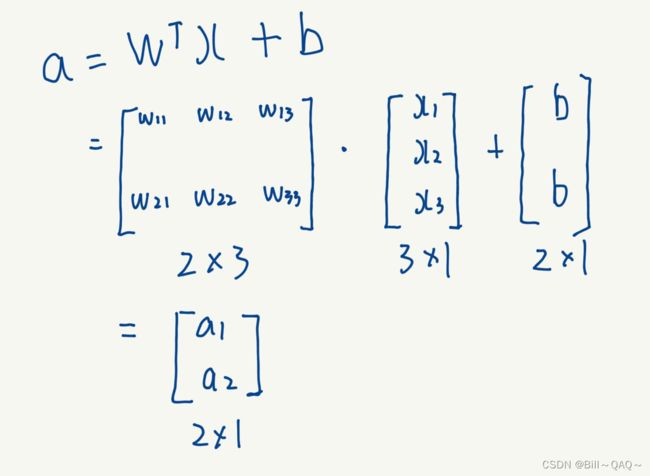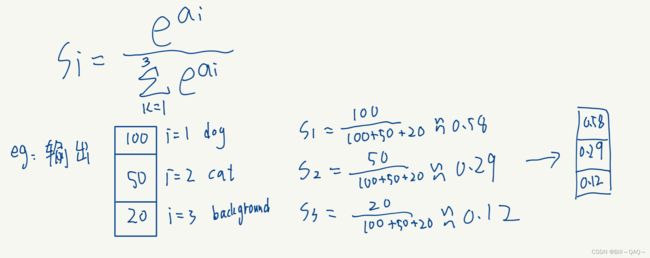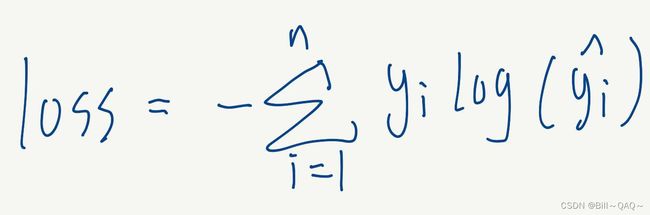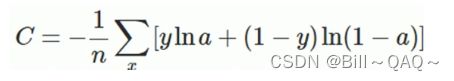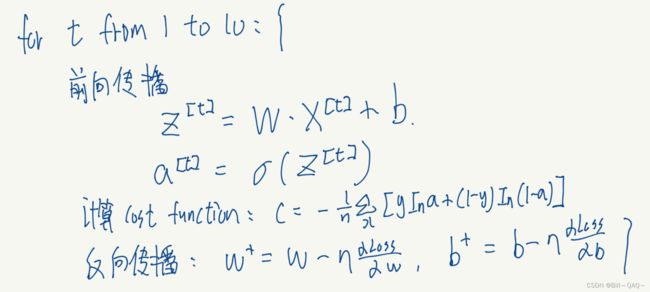手撕CNN卷积神经网络原理(一)
1.神经网络的计算
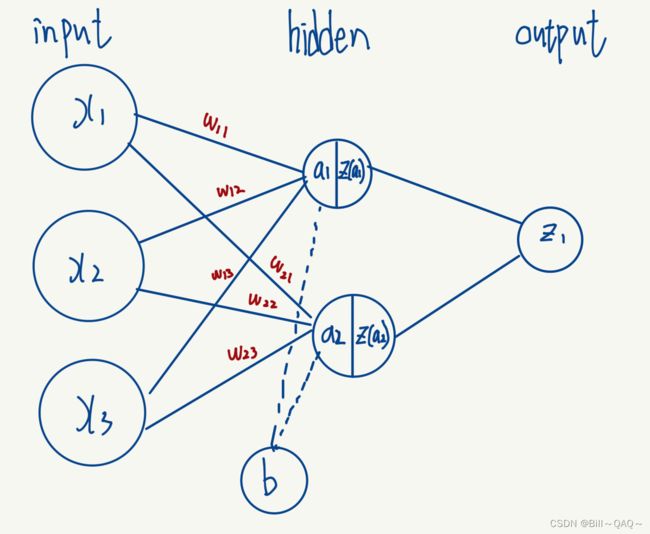
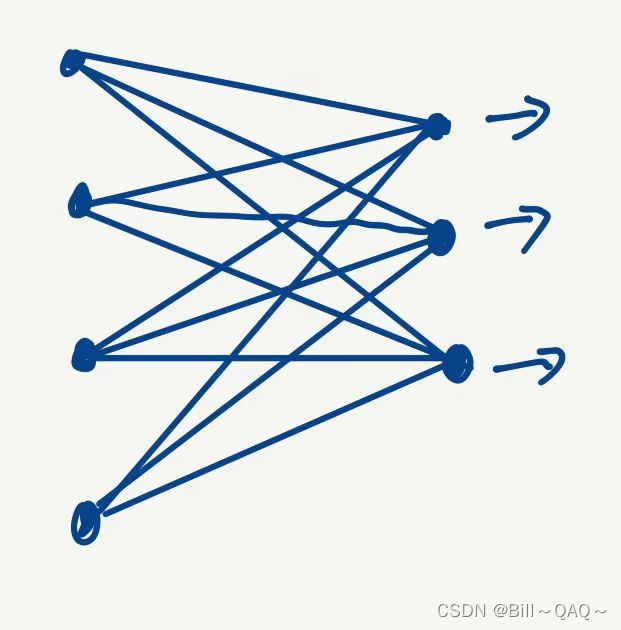
我们常见的比较简单的神经网络如下图所示
对于该神经网络,有以下感念
1.输入层(input layer),可以理解为数学中线性函数 y=kx+b 中的若干个x
2.权重w(weights):可以理解为数学中线性函数 y=kx+b 中的 k
3.偏执量b(bias):可以理解为数学中线性函数 y=kx+b 中的 b
4.a:可以理解为数学中线性函数 y=kx+b 中的y,但这个y不是该节点输出的结果
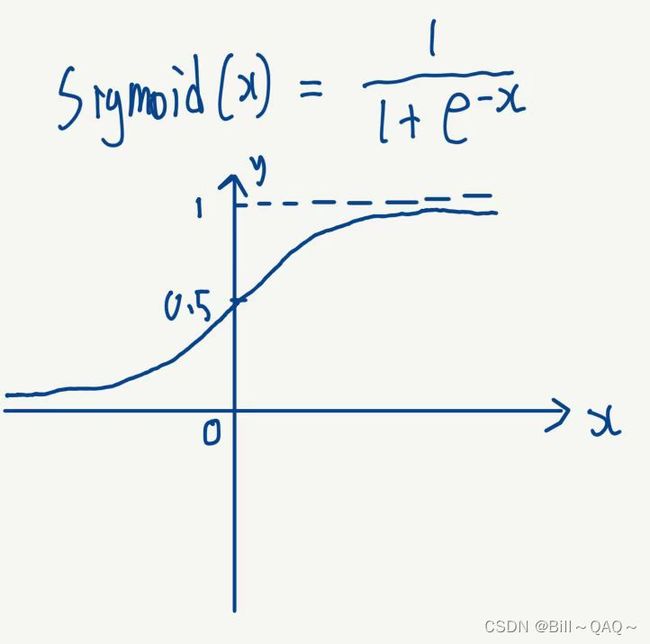
5.z()激活函数:用于将a进行非线性拟合得到更多更复杂的函数,常用的有一下两种:
sigmoid函数
Relu函数
现阶段深度学习中最常见的是Relu函数
知晓以上概念后,我们就可以写出如下的计算输出的式子
这样,我们就得到了隐藏(hidden layer)的输出,然后将这两个节点的结果再次用同样的方法进行计算(当然,其中的weight,bias可能不一样),就得到了神经网络的output输出
2.输入数据的矩阵计算
我们知道在神经网络中输入的数据是非常巨大的,动则成千上万,如果用上述函数的方法一个个进行计算会非常的耗时,因此在这里我们引入了矩阵计算
根据矩阵乘法的知识可知,在本例中![]() 是一个2*3的矩阵,x是一个3*1的矩阵,相乘后会得到一个2*1的矩阵,再将bias按照2*1的矩阵排列后相加,就得到了一个a的输出矩阵
是一个2*3的矩阵,x是一个3*1的矩阵,相乘后会得到一个2*1的矩阵,再将bias按照2*1的矩阵排列后相加,就得到了一个a的输出矩阵
至此,神经网络的基本概念和计算就讲到这里,下面我们来看一下卷积神经网络的计算,以及在应用中这两者要怎么结合到一起
3.卷积神经网络(CNN)
对输入的图像进行卷积神经网络处理,通常有以下步骤:
卷积层,激活函数,池化层,全连接层,softmax分类器
1.卷积层(conv)
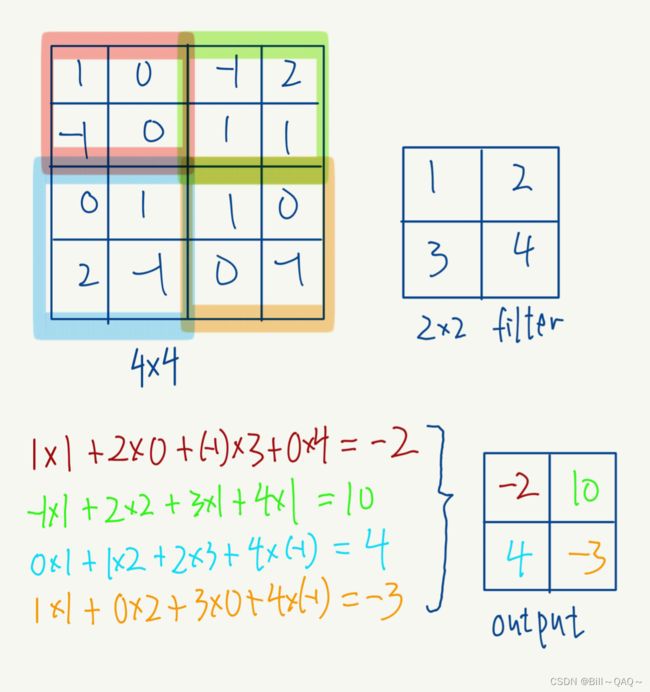
对输入的图像使用不同大小的卷积核(也叫滤波器filter)进行处理,关于卷积核是如何进行计算的如下图所示,这里先以单通道图像为例
这是一个4*4的单通道图像,图像中各点的像素如图所示,正常来说像素不会出现负数数值,我这里是为了便于计算
然后我还有一个2*2大小的卷积核,卷积核中的数值如图所示
在进行卷积核的计算之前,还需要了解如下概念
padding:在原图像外面补充多少圈0像素,本例原图padding=0
stride:卷积核在原图上每一次滑动几格,本例中我们将stride设定为2,也可以设为1
n=原图像大小,本例原图n=4
filter:卷积核大小,本例中filter=3
还有一个公式,我们可以提前计算出卷积处理后图像的大小,具体公式为
因此我们可以计算出,对原图进行一次卷积操作后,输出的图像大小应该是2*2的![]()
接下来我们进行卷积的计算,直接看图,我这里便于计算省略了bias,实际中应该在最后加上bias
好,接下来我们再推广到RGB彩色图像,也就是channel=3的图像
假设这是我的输入图像,有三个channel
这时候我们的应对也非常简单,就是把filter的channel也扩充到三个
然后每一层filter对应原图中的一个channel,对其进行卷积操作,这样我们就能得到三个结果,例如,假设经过本次卷积操作后,得到三个通道的结果如下,求和后加上bias得到最终结果
综上所述,在CNN中有以下两点
1.filter的channel数目必须与原图的channel一样
2.不管图像的channel是多少,经过一次卷积处理后生成的图像channel都是1,也就是说一个filter处理一次图像只能生成一个channel
2.激活函数层
这里使用的激活函数与前面神经网络讲到的一样,就是对每一个像素点的数值进行Relu,得到一个新的值作为该像素点的数值
3.池化层
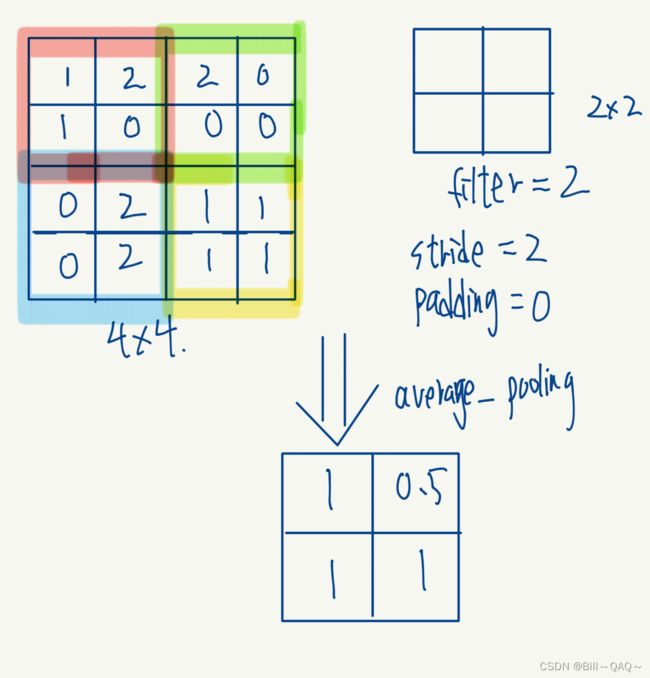
主要采用以下两种方式进行图像的池化处理
1.最大池化层,每移动一次filter,取原图filter范围内的最大值作为新的像素值
2.平均池化处理,每移动一次filter,取原图filter范围内数值的平均值作为新的像素值
同样的,对于pooling也有
4.实例
本例是单通道图像,对于多通道RGB图像,和前文一样,也是进行三层卷积计算后加和起来即可,不另作展示
1.首先将图像伸展为一个一维向量,这其中的每一个x都是神经网络中输入层的一个输入
2.再根据
可知,我们输出的hidden layer会有4个节点
3.根据卷积核计算出生成的图像像素数值,是一个2*2的图像,将其伸展为一维向量,那么这其中的每一个像素值就可以看作是每一个hidden layer的节点
4.根据卷积核中的计算关系,画出每一个输入和其输出的节点之间的weight权重(图中不同颜色所示)
5.由此可以看出,在卷积神经网络中,输入节点与hidden layer中的节点是一种稀疏连接,也就是说,不是所有的节点之间都有联系
6.这里没有展示池化,是因为输出图像已经是2*2大小,不需要池化了
如果将上图的过程按照神经网络中向量化的方式进行转换,就是
其中,没有连接的部分可以视为w=0
至于为什么![]() 长成这个样子,我的理解如下:
长成这个样子,我的理解如下:
我们将图片进行展开的时候,对其进行的是纵向展开成一维向量,对于卷积核的展开计算也是一样的,因此在计算的时候,我们要对其进行转置
5.全连接层
最后说说全连接层
在上述实例中,最终得到的输出矩阵是一个2*2的图像,展开后也就是一个4*1维的向量
如果我这个卷积网络要处理的是一个三分类的问题(猫,狗,背景),那么我使用的softmax分类器就要是一个3*1大小的向量,很显然,我们的输出结果不能直接放入softmax分类器中,所以就需要进行全连接处理,也就是“压缩”,把4*1的向量压缩成3*1的向量
如图所示,这里的全连接层其实就是开头讲到的全连接神经网络,通过将最后一次的输出作为全连接神经网络的输入层,经过神经网络计算后输出三个数值
从向量的角度来看就是:
我们的输出是一个4*1的向量,希望将他压缩成一个3*1的向量,那么根据矩阵的乘法,只需要在它前面乘上一个3*4的矩阵N即可,这个矩阵N中的每一个参数,就是全连接神经网络中的一个个权重w,道理与前面实例类似
由此这也引出了一个全连接层的一个问题,我们知道,在CNN中,使用不同大小,不同数目,不同stride,padding进行卷积操作,最终得到的图像大小是不一样的,同时,由于输入图像大小,即便进行一样的卷积操作,也会得到大小不同的输出图像。如果最后一个pooling每一次输出的图像大小都不一样,那么矩阵N的大小也要不停的变换,这样显然是做不到的
对于该方法目前已经有了解决办法,我们后续再聊
6.softmax分类器
对于前文FC层输出的结果来说,输出的3*1向量中的数值是任意的数,我们希望将其转换成概率,这就要使用一个类似激活函数的函数,softmax
softmax公式如下
其中3代表这是一个三分类问题,计算过程我直接举例说明了
在输出后,选择概率最高的那一个作为图像的输出结果,在我这个例子中,0.58概率最高,所以CNN判断这是一张dog的图片(具体结果对不对我们后面再说)
7.交叉熵
交叉熵就是用于判断我们预测的结果与实际的结果之间的差值(loss)的公式
在分类问题中,交叉熵的公式如下
yi是该图像的期望输出结果
我直接用例子解释这个公式吧,不然太抽象了
也就是说,上述公式其实可以进行化简,变成
不过此时要限定Sj必须是该图像实际分类被预测的概率,如果这张图像实际是dog,那就要带入softmax输出的dog那个概率,实际是cat就带入softmax输出的cat的概率
8.增大数据集时
以上的例子都是在单个输入的时候展现的,现在我们将其扩大
假设我有500个输入数据图片,将其按照向量的方式堆叠
对于这500个输出结果,我们对其中每一个都计算它的交叉熵loss,就可以得到500个样本的loss数值,根据cost function的有关定义,可以计算出这500个样本的总体cost function
x表示每一个样本,a表示该样本的预测值,y表示该样本的输出值,n表示样本的总数
这样我们就构建好了代价函数,随后对其进行反向传播,梯度下降即可,这种方法称为batch梯度下降,就是一次把所有数据全部读进去,以上过程成为完成了一个epoch
8.1 mini-batch梯度下降
在上面的例子中,我们将500个例子一口气全部读入神经网络,这样会耗费非常多的时间,而且在上面的例子中,我们是计算出了500个输出值,才能进行一次梯度下降。
所以,我们可以把500个训练集分成很多个batch,假设每一个batch的大小(batch-size)是50,那就是一共10个batch,如下图所示
接下来我们要做的就是,先将第一个batch放入网络,进行前向和反向传播,再放入第二个batch,进行前向和反向传播,如下图所示:
以上循环完成后,就是完成了一个epoch
可以看出,与batch梯度下降相比,同样是进行一个epoch,mini-batch进行了10次反向传播,进行了十次更新,而batch梯度下降的一个epoch只更新一次
8.2三种方式的比较
对于常见的batch-size
1.当batch-size=m的时候,也就是batch梯度下降,这时候我们的train loss曲线应该如下所示
因为我们每一个epoch都带入了所有的数据进行计算,所以每一个epoch都是在上一个epoch的最优基础上进行的,所以cost function一定会丝滑的下降
2.batch-size=1
这种情况下,梯度下降又被成为随机梯度下降,因为每次只采用一个样本,而每一个图片都有自己的特点,这就使得相邻两张图片的特征会变化很大,所拟合的w和b也会跳跃很大,所以下降的过程会非常的随机,有可能对上一张图片拟合的很好的参数不太适用于下一张图片。优点是快,如图中紫色
3.batch-size介于m和1之间
这种情况就是我们说的mini-batch,因为每一次都使用batch-size张图片,在上一个batch-size的基础上进行优化,所以cost函数会有一些小波动,但总体趋势还是向下