机器学习篇——MNIST手写数字识别

MNIST手写数字识别是调教一个完整的神经元来进行分类模型的构建应用，为什么说是一个完整神经元呢？因为它具备生物学上一个神经元的特征，除了有输入输出函数，还有一个激活函数，对应着生物学上神经元的阈值。

MNIST数据集的解读以及导入

这玩意说白了就是一个神经元处理分类问题（使用softmax分类，简单来说就是将概率转化为0-1区间的一个数字）。

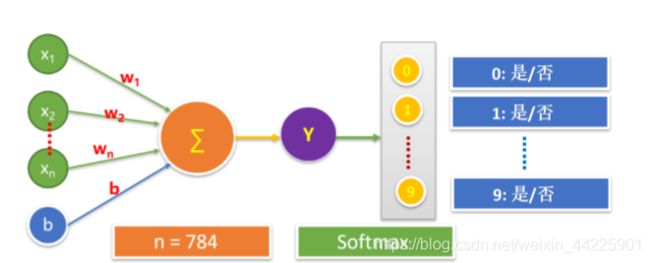
数据获取

MNIST手写数据集来自美国国家标准与技术研究所，由250个志愿者手写数字构成。
其中训练集55000，验证集5000，测试集10000。数据集可以在http://yann.lecun.com/exdb/mnist/获取。

读取数据集

# 导入相关库
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist=input_data.read_data_sets("D:/MNIST",one_hot=True)

# 数据集的形状
print("训练集 train 数量：",mnist.train.num_examples,
     ",验证集 validation 数量：",mnist.validation.num_examples,
     ",测试集 test 数量：",mnist.test.num_examples)

print("trains shape:",mnist.train.images.shape,
     ",labels shape:",mnist.train.labels.shape)


# 一副image的数据
len(mnist.train.images[0])
mnist.train.images[0].shape

# 重塑image数据
mnist.train.images[0].reshape(28,28)

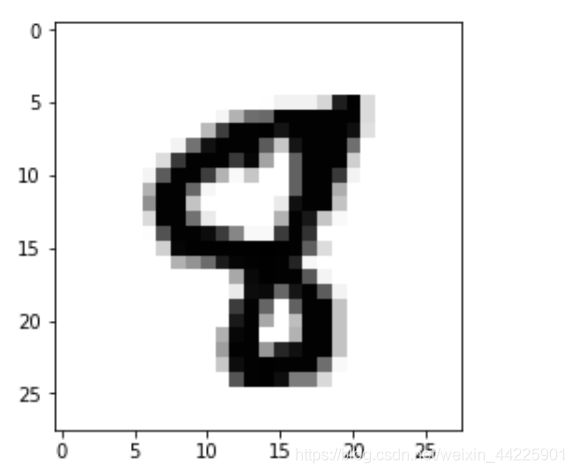
# 可视化 image
import matplotlib.pyplot as plt
def plot_image(image):
    plt.imshow(image.reshape(28,28),cmap="binary")
    plt.show()
    

# 可视化image图片
plot_image(mnist.train.images[6666])

# 理解标签
mnist.train.labels[666] # 独热编码是一种稀疏的向量，其中只有一个元素设为1，其他所有元素均设为0.
# 常用于表示用于有限个可能值的字符串后者标识符

'''

1.将离散特征的取值扩展到了欧式空间，离散特征的某个取值就对应欧式空间的某一个点
2.机器学习算法中，特征之间的距离计算或相似度的常用方法都是基于欧式空间的
3.将离散特征使用one-hot编码，会使特征值之间的距离计算会更加合理。
'''

# 独热编码取值
import numpy as np
np.argmax(mnist.train.labels[6666]) # argmax返回的是最大数的索引。

# 结果：8

# 一次批量读取多条数据
batch_images_xs,batch_labels_ys= \
    mnist.train.next_batch(batch_size=10) # next_batch()实现内部会对数据集先洗牌shuffle

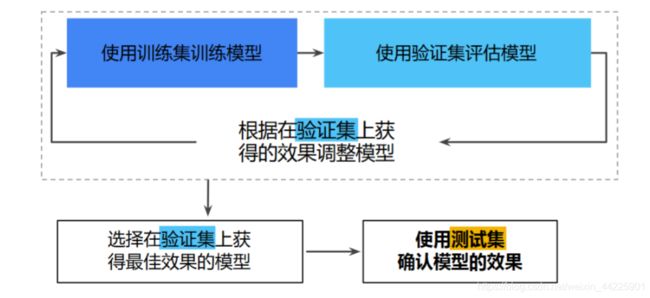
数据集的划分

模型构建

# 定义占位符
x=tf.placeholder(tf.float32,[None,784],name="X")
y=tf.placeholder(tf.float32,[None,10],name="Y")

# 定义模型变量(以正态分布的随机数初始化权重W，以常数0初始化偏置b)
W=tf.Variable(tf.random_normal([784,10]),name='W')
b=tf.Variable(tf.zeros([10]),name='b')

# 定义前向计算
forward=tf.matmul(x,W)+b

# 结果分类
pred=tf.nn.softmax(forward)
# 从预测问题到分类问题
# 从线性回归到逻辑回归

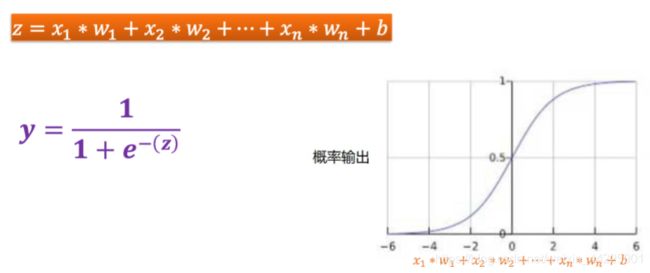
# 逻辑回归用于处理二元分类问题（二元分类问题目的是正确预测两个可能的标签中的一个），

# 需要将预测的输出值控制在[0，1]区间内
# sigmod函数生成的输出值正好具有这些特性

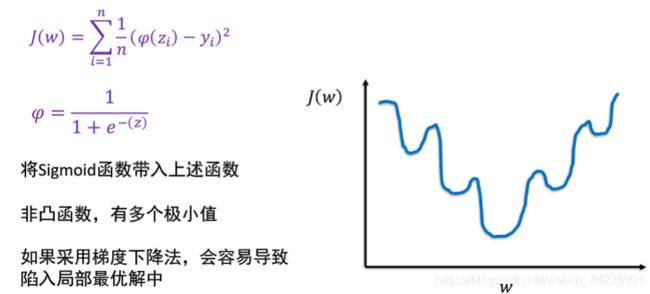
# 如果逻辑回归的损失函数还是使用平方损失，将sigmod函数代入上述函数
#则得到非凸函数，有多个极小值，还采用梯度下降算法，可能会导致现如局部优化最优解中。

# 二元逻辑回归的损失函数一般采用对数损失函数
# 交叉熵定义

# 定义交叉熵损失函数
loss_function=tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred),reduction_indices=1)) # 交叉熵

# 设置训练参数
train_epochs=60 # 训练轮数
batch_size=50 # 单次训练样本数（批次大小）
total_batch=int(mnist.train.num_examples/batch_size) # 一轮训练的批次数
display_step=1 # 显示粒度
learning_rate=0.01 # 学习率
# 分类模型构建与训练实践

# 选择优化器
optimizer=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)
# 梯度下降

# 检查预测类别tf.argmax(pred,1)与实际类别tf.argmax(y,1)的匹配情况
correct_prediction=tf.equal(tf.argmax(pred,1),tf.argmax(y,1))

# 准确率，将布尔值转化为浮点数，并计算平均值
accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32))

# 声明会话
sess=tf.Session()
# 变量初始化
init=tf.global_variables_initializer()
sess.run(init)

训练模型

# 训练模型
for epoch in range (train_epochs):
    for batch in range(total_batch):
        xs,ys=mnist.train.next_batch(batch_size) # 读取批次数据
        sess.run(optimizer,feed_dict={x:xs,y:ys})# 执行批次训练
  
    # total_batch批次训练完成之后，使用验证数据计算误差与准确率，验证集没有分批。
    loss,acc=sess.run([loss_function,accuracy],feed_dict={x:mnist.validation.images,y:mnist.validation.labels})

    # 打印训练过程中的详细信息
if (epoch+1)5 display_step=0:
    print("train_epoch:",'%02d'%(epoch+1),"loss=","{:.9f}".format(loss),\
         "accuracy=",'{:.4f}'.format(acc))
print("train finished!")

评估模型

# 在测试集上评估模型准确率
accu_test=sess.run(accuracy,feed_dict={x:mnist.test.images,y:mnist.test.labels})
print("test accuracy:",accu_test)

# 在验证集上评估模型准确率
accu_validation=sess.run(accuracy,feed_dict={x:mnist.validation.images,y:mnist.validation.labels})
print("validatin accuracy:",accu_validation)

# 在训练集上评估模型准确率
accu_train=sess.run(accuracy,feed_dict={x:mnist.train.images,y:mnist.train.labels})
print("tarin accuracy:",accu_train)

应用模型

独热码转化为十进制

# 由于pred预测结果是one-hot编码格式，所以需要转化为0~9数字
prediction_result=sess.run(tf.argmax(pred,1),feed_dict={x:mnist.test.images})

# 查看结果中的前十项
predictin_result[0:10]

结果可视化

# 定义可视化函数
import matplotlib.pyplot as plt
import numpy as np
def plot_images_lables_prediction(images, # 图像列表
                                  labels, # 标签列表 
                                  prediction, # 预测值列表
                                  index,# 从第index个开始显示
                                  num=10):# 缺省依次显示10副
    fig=plt.gcf() # 获取当前图表，get current figure
    fig.set_size_inches(10,12) # 1英寸等于2.54cm
    if num>25:
        num=25 # 最多显示25个子图
    for i in range(0,num):
        ax=plt.subplot(5,5,i+1) # 获取当前要处理的子图
        
        ax.imshow(np.reshape(images[index],(28,28)),
                  cmap='binary') # 显示第index个图像       
        title="labels="+str(np.argmax(labels[index])) # 构建该图上要显示的title信息
        if len(prediction)>0:
            title+=",predict="+str(prediciton[index])

        ax.set_title(title.frontsize=10) # 显示图上的title
        ax.set_xticks([]) # 不显示坐标轴
        ax.set_yticks([])
        index+=1
    plot.show()

# 可视化预测结果
plot_images_labels_prediction(mnist.test.images,
                             mnist.test.labels,
                             prediction_result,666,666)

到这里大体框架就结束了，当然你也可以继续完善，如加入tensorboard可视化代码，定义更好的超参数等等。
这是严格意义上第一个真正的神经元实现。个人感觉还是特别有意思的，人类的智慧真的可以无限的扩展。学科交叉能创造出无法想象的精彩，真的让人叹为观止！