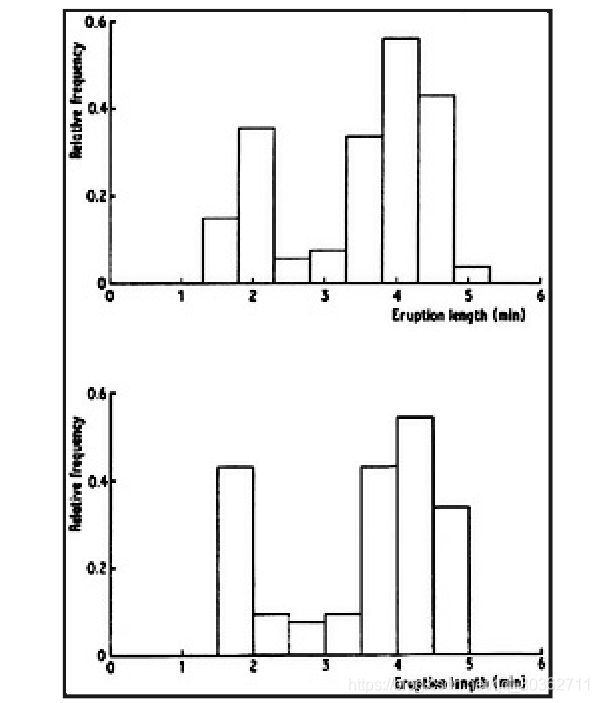
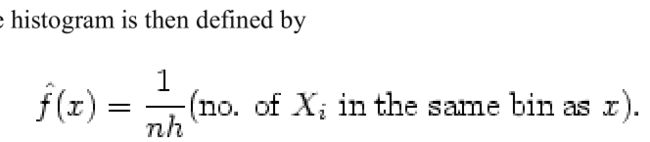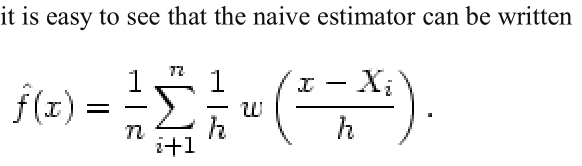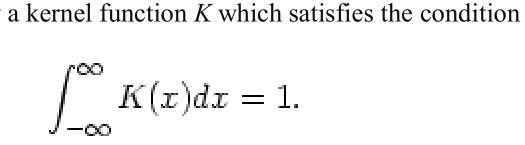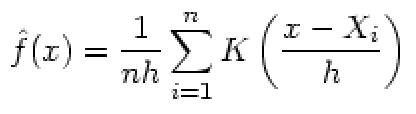- 卷积神经网络(Convolutional Neural Network, CNN)
不想秃头的程序
神经网络语音识别人工智能深度学习网络卷积神经网络
卷积神经网络(ConvolutionalNeuralNetwork,CNN)是一种专门用于处理图像、视频等网格数据的深度学习模型。它通过卷积层自动提取数据的特征,并利用空间共享权重和池化层减少参数量和计算复杂度,成为计算机视觉领域的核心技术。以下是CNN的详细介绍:一、核心思想CNN的核心目标是从图像中自动学习层次化特征,并通过空间共享权重和平移不变性减少参数量和计算成本。其关键组件包括:卷积层(
- ResNet(Residual Network)
不想秃头的程序
神经网络语音识别人工智能深度学习网络残差网络神经网络
ResNet(ResidualNetwork)是深度学习中一种经典的卷积神经网络(CNN)架构,由微软研究院的KaimingHe等人在2015年提出。它通过引入残差连接(SkipConnection)解决了深度神经网络中的梯度消失问题,使得网络可以训练极深的模型(如上百层),并在图像分类、目标检测、语义分割等任务中取得了突破性成果。以下是ResNet的详细介绍:一、核心思想ResNet的核心创新是
- P25:LSTM实现糖尿病探索与预测
?Agony
lstm人工智能rnn
本文为365天深度学习训练营中的学习记录博客原作者:K同学啊一、相关技术1.LSTM基本概念LSTM(长短期记忆网络)是RNN(循环神经网络)的一种变体,它通过引入特殊的结构来解决传统RNN中的梯度消失和梯度爆炸问题,特别适合处理序列数据。结构组成:遗忘门:决定丢弃哪些信息,通过sigmoid函数输出0-1之间的值,表示保留或遗忘的程度。输入门:决定更新哪些信息,同样通过sigmoid函数控制更新
- 【机器学习&深度学习】反向传播机制
目录一、一句话定义二、类比理解三、为什重要?四、用生活例子解释:神经网络=烹饪机器人4.1第一步:尝一口(前向传播)4.2第二步:倒着推原因(反向传播)五、换成人工智能流程说一遍六、图示类比:找山顶(最优参数)七、总结一句人话八、PyTorch代码示例:亲眼看到每一层的梯度九、梯度=损失函数对参数的偏导数十、类比总结反向传播(Backpropagation)是神经网络中训练过程的核心机制,它就像“
- 人脸识别算法赋能园区无人超市安防升级
智驱力人工智能
算法人工智能边缘计算人脸识别智慧园区智慧工地智慧煤矿
人脸识别算法赋能园区无人超市安防升级正文在园区无人超市的运营管理中,传统安防手段依赖人工巡检或基础监控设备,存在响应滞后、误报率高、环境适应性差等问题。本文从技术背景、实现路径、功能优势及应用场景四个维度,阐述如何通过人脸识别检测、人员入侵算法及疲劳检测算法的协同应用,构建高效、精准的智能安防体系。一、技术背景:视觉分析算法的核心支撑人脸识别算法基于深度学习的卷积神经网络(CNN)模型,通过提取面
- 拼多多商品详情API接口:社交电商的得力助手
lovelin+vI7809804594
图搜索算法算法人工智能爬虫API
在"人找货"向"货找人"的范式转移中,拼多多凭借社交裂变模式重塑中国电商格局。其商品详情API接口作为连接6.8亿消费者与1500万商家的数字纽带,日均调用量突破100亿次,支撑着秒杀、拼团、砍价等特色玩法。这一技术工具不仅是数据通道,更是社交电商生态的神经中枢,驱动着用户增长、流量分发和交易转化的全链路优化。一、技术解码:商品详情API的架构设计与核心能力高并发架构体系分片存储策略:采用TIDB
- 误差的回响:反向传播算法与神经网络的惊天逆转
田园Coder
人工智能科普人工智能科普
当专家系统在20世纪80年代初期大放异彩,成为人工智能实用化的耀眼明星时,另一股曾经被宣判“死刑”的力量——连接主义(神经网络)——正在寒冬的冻土下悄然涌动,孕育着一场惊天动地的复苏。马文·明斯基和西摩·帕尔特在1969年《感知机》专著中那精准而冷酷的理论批判,如同沉重的封印,将多层神经网络的研究禁锢了近二十年。他们指出的核心死结——缺乏有效算法来训练具有隐藏层的网络——仿佛一道无法逾越的天堑。单
- MATLAB实现WOA-BP鲸鱼优化算法优化BP神经网络多输入单输出回归预测(含模型描述及示例代码)
nantangyuxi
MATLAB含模型描述及示例代码算法matlab神经网络大数据人工智能深度学习机器学习
目录MATLAB实现WOA-BP鲸鱼优化算法优化BP神经网络多输入单输出回归预测(多指标,多图)1项目背景介绍...1项目目标与意义...2项目挑战...3项目特点与创新...5<
- 量子机器学习前沿:量子神经网络与混合量子-经典算法
软考和人工智能学堂
人工智能#深度学习Python开发经验量子计算
1.量子计算基础1.1量子比特与量子门importnumpyasnpfromqiskitimportQuantumCircuit,Aer,executefromqiskit.visualizationimportplot_histogram#单量子比特操作演示defsingle_qubit_demo():qc=QuantumCircuit(1)qc.h(0)#Hadamard门创建叠加态qc.rz
- Python打卡:Day39
剑桥折刀s
python
知识点回顾图像数据的格式:灰度和彩色数据模型的定义显存占用的4种地方模型参数+梯度参数优化器参数数据批量所占显存神经元输出中间状态batchisize和训练的关系@浙大疏锦行
- 【机器学习】数学基础——张量(傻瓜篇)
一叶千舟
深度学习【理论】机器学习人工智能
目录前言一、张量的定义1.标量(0维张量)2.向量(1维张量)3.矩阵(2维张量)4.高阶张量(≥3维张量)二、张量的数学表示2.1张量表示法示例三、张量的运算3.1常见张量运算四、张量在深度学习中的应用4.1PyTorch示例:张量在神经网络中的运用五、总结:张量的多维世界延伸阅读前言在机器学习、深度学习以及物理学中,张量是一个至关重要的概念。无论是在人工智能领域的神经网络中,还是在高等数学、物
- 【机器学习实战】Datawhale夏令营2:深度学习回顾
城主_全栈开发
机器学习机器学习深度学习人工智能
#DataWhale夏令营#ai夏令营文章目录1.深度学习的定义1.1深度学习&图神经网络1.2机器学习和深度学习的关系2.深度学习的训练流程2.1数学基础2.1.1梯度下降法基本原理数学表达步骤学习率α梯度下降的变体2.1.2神经网络与矩阵网络结构表示前向传播激活函数反向传播批处理卷积操作参数更新优化算法正则化初始化2.2激活函数Sigmoid函数:Tanh函数:ReLU函数(Rectified
- RNN笔记
sjtu_哈基坤
LLM随笔rnn笔记人工智能
来源见此处概述RNN(RecurrentNeuralNetwork)RNN之所以称为循环神经网络,是因为一个序列的当前的输出与前面的输出也有关.具体表现是网络会对前面的信息进行记忆并且应用于当前输出的计算中.即隐藏层之间的节点也是有连接的.并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出.理论上RNN能对任何长度的序列进行处理,但是在实践中,为了降低复杂性,往往假设当前状态只与前面几
- 从0开始学习计算机视觉--Day04--线性分类
Chef_Chen
学习计算机视觉分类
从宏观来看,卷积网络可以看做是由一个个不同的神经网络组件组合而成,就像积木一样通过不同类型的组件搭建形成,其中线性分类器是一个很重要的组件,在很多卷积网络中都有用到,所以了解清楚它的工作原理对我们后续的学习会有很大的帮助。线性分类器是参数模型中最简单,最基础的例子,下面我们用输入图片输出图片分类的模型的例子来更进一步地了解它。首先,我们输入一张图片到模型中,输入后我们就会得到f(x,W),x指的是
- 如何设计和训练大模型(神经网络):从入门到精通!
“学习一门技术,先找一套工具和理论研究下去;千万不要反复横跳,什么都想学”大模型作为未来重要的发展方向,很多人想学习大模型技术,但又苦于无从下手;而本公众号前前后后也写过一些怎么学习大模型技术的方法论;但大部分都是从应用的角度作为切入点。但是,有一个问题就是,如果你是一个技术从业者,想学习和设计一款属于自己的大模型,应该怎么做?设计一个自己的大模型大模型作为一门快速发展的新型技术,其理论与实现也是
- Linux网卡Bond设置
杨了个杨8982
linux基础linux服务器网络
一、网卡Bond介绍1.概念网卡Bond是一种网络技术,也被称为链路聚合、端口绑定或接口绑定,能将多个物理网络接口组合成一个逻辑接口。2.工作原理及作用bond模式增加网络带宽提高网络可靠性实现负载均衡适用场景备注Mode0:Balance-RR(轮询模式)原理:依次将数据包按顺序分配到各个成员接口发送。例如有三个成员接口,第一个数据包从接口1发送,第二个从接口2发送,第三个从接口3发送,之后循环
- VLLM:虚拟大型语言模型(Virtual Large Language Model)
大霸王龙
语言模型人工智能自然语言处理
VLLM:虚拟大型语言模型(VirtualLargeLanguageModel)VLLM指的是一种基于云计算的大型语言模型的虚拟实现。它通常是指那些由多个服务器组成的分布式计算环境中的复杂机器学习模型,这些模型能够处理和理解大量的文本数据。VLLM的核心是“大型语言模型”,这是一种通过深度神经网络训练的算法,能够在理解和生成人类语言方面表现出极高的能力。解释:虚拟:意味着这个模型不是在单个物理设备
- Day7 神经网络的矩阵基础
神经网络的矩阵基础一、矩阵的基本概念1.矩阵的定义与类型矩阵是一个按照长方阵列排列的复数或实数集合。在神经网络中,矩阵是表示和操作数据的基本结构。常见的矩阵类型包括:方阵:行数和列数相等的矩阵,记作n×nn×nn×n矩阵。行向量:只有一行的矩阵,可以看作是一个n×1n×1n×1的矩阵。列向量:只有一列的矩阵,可以看作是一个1×n1×n1×n的矩阵。单位矩阵:主对角线上的元素为1,其余元素为0的方阵
- 【软件系统架构】系列四:嵌入式软件-NPU(神经网络处理器)系统及模板
目录一、什么是NPU?二、NPU与CPU/GPU/DSP对比三、NPU的工作原理核心结构:数据流架构:四、NPU芯片架构(简化图)五、NPU的优势六、NPU应用场景视觉识别语音识别自动驾驶智能监控AIoT设备七、主流NPU芯片/架构实例八、开发者工具生态(通用)九、NPU集成建议(嵌入式开发场景)十、NPU芯片选型对比+模型部署流程+嵌入式工程模板1.主流NPU芯片选型对比表2.模型部署流程(以T
- DAY 33 简单的神经网络
2401_84854050
python打卡神经网络深度学习人工智能
1.数据预处理(0)准备数据、划分数据#仍然用4特征,3分类的鸢尾花数据集作为我们今天的数据集fromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitimportnumpyasnp#加载鸢尾花数据集iris=load_iris()X=iris.data#特征数据y=iris.target
- 入选 ICML 2025!哈佛医学院等推出全球首个 HIE 领域临床思维图谱模型,神经认知结果预测任务上性能提升 15%
hyperai
在人工智能技术突飞猛进的当下,大型视觉-语言模型(LVLMs)正以惊人的速度重塑多个领域的认知边界。在自然图像与视频分析领域,这类模型依托先进的神经网络架构、海量标注数据集与强大算力支持,已能精准完成物体识别、场景解析等高阶任务。而在自然语言处理领域,LVLMs通过对TB级文本语料的学习,在机器翻译、文本摘要、情感分析等任务上达到专业级水准,其生成的学术摘要甚至能精准提炼医学文献的核心结论。然而当
- 第2篇:路由基础——Gin的核心功能
GO兔
gingolang后端
引言:为什么路由是Web框架的"神经网络"路由是Web应用的骨架,它决定了客户端请求如何被服务器处理和响应。想象一个没有路由的Web应用——就像一座没有路标和门牌的城市,用户根本无法找到目的地。Gin框架的高性能很大程度上归功于其基于RadixTree(基数树)实现的路由引擎,这使得路由匹配速度达到了O(logn)的时间复杂度。对于初中级工程师来说,掌握路由设计不仅是实现API的基础,更是写出高性
- 【深度学习解惑】训练RNN时如何解决梯度消失或梯度爆炸?
训练RNN时如何解决梯度消失或梯度爆炸?1.引言与背景介绍循环神经网络(RNN)是处理序列数据的核心模型,但在训练过程中面临两大挑战:梯度消失(GradientVanishing)和梯度爆炸(GradientExplosion)。梯度消失导致长距离依赖难以学习(如文本中相距50个词的关联),而梯度爆炸会造成参数剧烈震荡甚至数值溢出(NaN值)。本文系统分析问题根源并提供工程级解决方案。2.原理解释
- 深入理解AI人工智能深度学习的原理架构
AI学长带你学AI
人工智能深度学习ai
深入理解AI人工智能深度学习的原理架构关键词:人工智能、深度学习、原理架构、神经网络、数学模型摘要:本文旨在深入剖析AI人工智能深度学习的原理架构。首先介绍了深度学习的背景,包括其目的、预期读者、文档结构和相关术语。接着阐述了深度学习的核心概念,如神经网络、激活函数等,并通过示意图和流程图进行直观展示。详细讲解了核心算法原理,如反向传播算法,并给出Python代码示例。同时,介绍了深度学习中的数学
- 【大模型】【机器学习】【面试宝典】
曾小文
机器学习面试人工智能
面试热点科普:BatchNorm和LayerNorm有什么区别?在深度学习面试中,经常会被问到模型训练稳定性相关的问题。其中两个关键词BatchNorm和LayerNorm绝对是高频词!今天就带大家快速梳理两者的核心区别,用最通俗的方式掌握它们的原理和应用场景,面试不再含糊!1.什么是归一化(Normalization)?归一化是神经网络训练过程中的一项重要技巧,目的是:缓解梯度爆炸/消失加快收敛
- 如何“调优”我们自身的人体系统?
SugarPPig
笔记养生
文章主题本文主要围绕如何通过科学方法优化人体系统,提升健康、学习和工作效率,延缓衰老等展开,内容涉及睡眠、饮食、心态、学习、大脑健康和长寿等多个方面,基于斯坦福神经科学教授AndrewHuberman等人的研究成果和实践经验分享。核心内容一、睡眠原理生物钟控制:生物钟影响体内化学物质变化和体温变化,进而影响内在状态和外在行为。皮质醇和肾上腺素让人早上醒来,同时设定松果体释放褪黑素的倒计时,让人在十
- LLM模型的一些思考
巴基海贼王
nlp
对通用LLM模型进行Fine-tuning操作(SFT,supervisedfinetuning),带来的影响往往是有害的?从表象看,使用领域数据对LLM做Fine-tuning,通常会造成灾难性的“灾难遗忘”问题。简单点儿说,SFT在赋予对领域知识理解能力的同时,由于修正模型参数,导致模型遗忘之前学会的某些知识。目前的“智能=压缩”的理论是否正确?LLM的压缩能力是否可以拆解成单个神经元的“压缩
- OpenCV边缘填充方式详解
慕婉0307
opencv基础opencv计算机视觉人工智能
一、边缘填充概述在图像处理中,边缘填充(BorderPadding)是一项基础而重要的技术,特别是在进行卷积操作(如滤波、边缘检测等)时,处理图像边缘像素需要用到周围的像素值。由于图像边缘的像素没有完整的邻域,因此需要通过某种方式对图像边界进行扩展。边缘填充的主要应用场景包括:图像滤波(如高斯滤波、中值滤波等)卷积神经网络(CNN)中的卷积层形态学操作(如膨胀、腐蚀)图像特征提取二、OpenCV中
- 数字海洋生命可视化系统(代码邂逅深蓝)
四段数学方程正演绎着一场跨越代码与生命的奇妙共生。这组“数字海洋生命可视化系统”以Python为浪,用算法作礁,让小水母、蚰蜒、虫子与大水母在黑色幕布上绽放出超越自然的流光。指尖轻点“小水母”,10000个数据点便化作剔透的伞状体,触须随π/20的时间步长摇曳,5倍余弦函数编织的波纹在彩虹色与深海蓝间切换——当q值驱动的光点跃动时,仿佛真有月光穿透海面,让每个像素都成为发光水母的神经突触。而“蚰蜒
- 用 PyTorch 构建液态神经网络(LNN):下一代动态深度学习模型
点我头像干啥
AI深度学习pytorch神经网络
引言在深度学习领域,研究人员不断探索更接近生物神经系统工作方式的模型。液态神经网络(LiquidNeuralNetworks,LNN)正是这样一种受生物神经元动态特性启发的创新架构。本文将带你了解LNN的核心概念,并展示如何使用PyTorch实现这种前沿模型。一、什么是液态神经网络?液态神经网络是由MIT研究人员提出的一种新型神经网络架构,它模仿了生物神经系统的几个关键特性:动态连接:神经元之间的
- Java实现的简单双向Map,支持重复Value
superlxw1234
java双向map
关键字:Java双向Map、DualHashBidiMap
有个需求,需要根据即时修改Map结构中的Value值,比如,将Map中所有value=V1的记录改成value=V2,key保持不变。
数据量比较大,遍历Map性能太差,这就需要根据Value先找到Key,然后去修改。
即:既要根据Key找Value,又要根据Value
- PL/SQL触发器基础及例子
百合不是茶
oracle数据库触发器PL/SQL编程
触发器的简介;
触发器的定义就是说某个条件成立的时候,触发器里面所定义的语句就会被自动的执行。因此触发器不需要人为的去调用,也不能调用。触发器和过程函数类似 过程函数必须要调用,
一个表中最多只能有12个触发器类型的,触发器和过程函数相似 触发器不需要调用直接执行,
触发时间:指明触发器何时执行,该值可取:
before:表示在数据库动作之前触发
- [时空与探索]穿越时空的一些问题
comsci
问题
我们还没有进行过任何数学形式上的证明,仅仅是一个猜想.....
这个猜想就是; 任何有质量的物体(哪怕只有一微克)都不可能穿越时空,该物体强行穿越时空的时候,物体的质量会与时空粒子产生反应,物体会变成暗物质,也就是说,任何物体穿越时空会变成暗物质..(暗物质就我的理
- easy ui datagrid上移下移一行
商人shang
js上移下移easyuidatagrid
/**
* 向上移动一行
*
* @param dg
* @param row
*/
function moveupRow(dg, row) {
var datagrid = $(dg);
var index = datagrid.datagrid("getRowIndex", row);
if (isFirstRow(dg, row)) {
- Java反射
oloz
反射
本人菜鸟,今天恰好有时间,写写博客,总结复习一下java反射方面的知识,欢迎大家探讨交流学习指教
首先看看java中的Class
package demo;
public class ClassTest {
/*先了解java中的Class*/
public static void main(String[] args) {
//任何一个类都
- springMVC 使用JSR-303 Validation验证
杨白白
springmvc
JSR-303是一个数据验证的规范,但是spring并没有对其进行实现,Hibernate Validator是实现了这一规范的,通过此这个实现来讲SpringMVC对JSR-303的支持。
JSR-303的校验是基于注解的,首先要把这些注解标记在需要验证的实体类的属性上或是其对应的get方法上。
登录需要验证类
public class Login {
@NotEmpty
- log4j
香水浓
log4j
log4j.rootCategory=DEBUG, STDOUT, DAILYFILE, HTML, DATABASE
#log4j.rootCategory=DEBUG, STDOUT, DAILYFILE, ROLLINGFILE, HTML
#console
log4j.appender.STDOUT=org.apache.log4j.ConsoleAppender
log4
- 使用ajax和history.pushState无刷新改变页面URL
agevs
jquery框架Ajaxhtml5chrome
表现
如果你使用chrome或者firefox等浏览器访问本博客、github.com、plus.google.com等网站时,细心的你会发现页面之间的点击是通过ajax异步请求的,同时页面的URL发生了了改变。并且能够很好的支持浏览器前进和后退。
是什么有这么强大的功能呢?
HTML5里引用了新的API,history.pushState和history.replaceState,就是通过
- centos中文乱码
AILIKES
centosOSssh
一、CentOS系统访问 g.cn ,发现中文乱码。
于是用以前的方式:yum -y install fonts-chinese
CentOS系统安装后,还是不能显示中文字体。我使用 gedit 编辑源码,其中文注释也为乱码。
后来,终于找到以下方法可以解决,需要两个中文支持的包:
fonts-chinese-3.02-12.
- 触发器
baalwolf
触发器
触发器(trigger):监视某种情况,并触发某种操作。
触发器创建语法四要素:1.监视地点(table) 2.监视事件(insert/update/delete) 3.触发时间(after/before) 4.触发事件(insert/update/delete)
语法:
create trigger triggerName
after/before
- JS正则表达式的i m g
bijian1013
JavaScript正则表达式
g:表示全局(global)模式,即模式将被应用于所有字符串,而非在发现第一个匹配项时立即停止。 i:表示不区分大小写(case-insensitive)模式,即在确定匹配项时忽略模式与字符串的大小写。 m:表示
- HTML5模式和Hashbang模式
bijian1013
JavaScriptAngularJSHashbang模式HTML5模式
我们可以用$locationProvider来配置$location服务(可以采用注入的方式,就像AngularJS中其他所有东西一样)。这里provider的两个参数很有意思,介绍如下。
html5Mode
一个布尔值,标识$location服务是否运行在HTML5模式下。
ha
- [Maven学习笔记六]Maven生命周期
bit1129
maven
从mvn test的输出开始说起
当我们在user-core中执行mvn test时,执行的输出如下:
/software/devsoftware/jdk1.7.0_55/bin/java -Dmaven.home=/software/devsoftware/apache-maven-3.2.1 -Dclassworlds.conf=/software/devs
- 【Hadoop七】基于Yarn的Hadoop Map Reduce容错
bit1129
hadoop
运行于Yarn的Map Reduce作业,可能发生失败的点包括
Task Failure
Application Master Failure
Node Manager Failure
Resource Manager Failure
1. Task Failure
任务执行过程中产生的异常和JVM的意外终止会汇报给Application Master。僵死的任务也会被A
- 记一次数据推送的异常解决端口解决
ronin47
记一次数据推送的异常解决
需求:从db获取数据然后推送到B
程序开发完成,上jboss,刚开始报了很多错,逐一解决,可最后显示连接不到数据库。机房的同事说可以ping 通。
自已画了个图,逐一排除,把linux 防火墙 和 setenforce 设置最低。
service iptables stop
- 巧用视错觉-UI更有趣
brotherlamp
UIui视频ui教程ui自学ui资料
我们每个人在生活中都曾感受过视错觉(optical illusion)的魅力。
视错觉现象是双眼跟我们开的一个玩笑,而我们往往还心甘情愿地接受我们看到的假象。其实不止如此,视觉错现象的背后还有一个重要的科学原理——格式塔原理。
格式塔原理解释了人们如何以视觉方式感觉物体,以及图像的结构,视角,大小等要素是如何影响我们的视觉的。
在下面这篇文章中,我们首先会简单介绍一下格式塔原理中的基本概念,
- 线段树-poj1177-N个矩形求边长(离散化+扫描线)
bylijinnan
数据结构算法线段树
package com.ljn.base;
import java.util.Arrays;
import java.util.Comparator;
import java.util.Set;
import java.util.TreeSet;
/**
* POJ 1177 (线段树+离散化+扫描线),题目链接为http://poj.org/problem?id=1177
- HTTP协议详解
chicony
http协议
引言
- Scala设计模式
chenchao051
设计模式scala
Scala设计模式
我的话: 在国外网站上看到一篇文章,里面详细描述了很多设计模式,并且用Java及Scala两种语言描述,清晰的让我们看到各种常规的设计模式,在Scala中是如何在语言特性层面直接支持的。基于文章很nice,我利用今天的空闲时间将其翻译,希望大家能一起学习,讨论。翻译
- 安装mysql
daizj
mysql安装
安装mysql
(1)删除linux上已经安装的mysql相关库信息。rpm -e xxxxxxx --nodeps (强制删除)
执行命令rpm -qa |grep mysql 检查是否删除干净
(2)执行命令 rpm -i MySQL-server-5.5.31-2.el
- HTTP状态码大全
dcj3sjt126com
http状态码
完整的 HTTP 1.1规范说明书来自于RFC 2616,你可以在http://www.talentdigger.cn/home/link.php?url=d3d3LnJmYy1lZGl0b3Iub3JnLw%3D%3D在线查阅。HTTP 1.1的状态码被标记为新特性,因为许多浏览器只支持 HTTP 1.0。你应只把状态码发送给支持 HTTP 1.1的客户端,支持协议版本可以通过调用request
- asihttprequest上传图片
dcj3sjt126com
ASIHTTPRequest
NSURL *url =@"yourURL";
ASIFormDataRequest*currentRequest =[ASIFormDataRequest requestWithURL:url];
[currentRequest setPostFormat:ASIMultipartFormDataPostFormat];[currentRequest se
- C语言中,关键字static的作用
e200702084
C++cC#
在C语言中,关键字static有三个明显的作用:
1)在函数体,局部的static变量。生存期为程序的整个生命周期,(它存活多长时间);作用域却在函数体内(它在什么地方能被访问(空间))。
一个被声明为静态的变量在这一函数被调用过程中维持其值不变。因为它分配在静态存储区,函数调用结束后并不释放单元,但是在其它的作用域的无法访问。当再次调用这个函数时,这个局部的静态变量还存活,而且用在它的访
- win7/8使用curl
geeksun
win7
1. WIN7/8下要使用curl,需要下载curl-7.20.0-win64-ssl-sspi.zip和Win64OpenSSL_Light-1_0_2d.exe。 下载地址:
http://curl.haxx.se/download.html 请选择不带SSL的版本,否则还需要安装SSL的支持包 2. 可以给Windows增加c
- Creating a Shared Repository; Users Sharing The Repository
hongtoushizi
git
转载自:
http://www.gitguys.com/topics/creating-a-shared-repository-users-sharing-the-repository/ Commands discussed in this section:
git init –bare
git clone
git remote
git pull
git p
- Java实现字符串反转的8种或9种方法
Josh_Persistence
异或反转递归反转二分交换反转java字符串反转栈反转
注:对于第7种使用异或的方式来实现字符串的反转,如果不太看得明白的,可以参照另一篇博客:
http://josh-persistence.iteye.com/blog/2205768
/**
*
*/
package com.wsheng.aggregator.algorithm.string;
import java.util.Stack;
/**
- 代码实现任意容量倒水问题
home198979
PHP算法倒水
形象化设计模式实战 HELLO!架构 redis命令源码解析
倒水问题:有两个杯子,一个A升,一个B升,水有无限多,现要求利用这两杯子装C
- Druid datasource
zhb8015
druid
推荐大家使用数据库连接池 DruidDataSource. http://code.alibabatech.com/wiki/display/Druid/DruidDataSource DruidDataSource经过阿里巴巴数百个应用一年多生产环境运行验证,稳定可靠。 它最重要的特点是:监控、扩展和性能。 下载和Maven配置看这里: http
- 两种启动监听器ApplicationListener和ServletContextListener
spjich
javaspring框架
引言:有时候需要在项目初始化的时候进行一系列工作,比如初始化一个线程池,初始化配置文件,初始化缓存等等,这时候就需要用到启动监听器,下面分别介绍一下两种常用的项目启动监听器
ServletContextListener
特点: 依赖于sevlet容器,需要配置web.xml
使用方法:
public class StartListener implements
- JavaScript Rounding Methods of the Math object
何不笑
JavaScriptMath
The next group of methods has to do with rounding decimal values into integers. Three methods — Math.ceil(), Math.floor(), and Math.round() — handle rounding in differen