使用KMeans对iris数据集聚类

一、聚类分析的基本知识

聚类分析也称聚类，它与分类是不同的，分类的目标变量是已知的，每个样本都存在类标签，而聚类的目标变量是事先不知道的，聚类的样本类别没有被预先定义出来。聚类是根据聚类算法或样本对象划分成两个以上的子集，每个子集称为一个簇，簇中对象因特征属性值接近而彼此相似，不同簇对象之间则彼此存在差异，簇内的对象越相似，聚类的效果就越好。

聚类分析是将相似的对象归为同一簇，将不相似的对象归为不同簇，这就需要一种计算方法来度量相似程度，常用的相似度计算方法有欧式距离、余弦距离、曼哈顿距离以及闵可夫斯基距离。

二、K-Means聚类算法

K-means算法中的K表示的是聚类为K个簇，means代表取每一个聚类中数据值的均值作为该簇的中心，也可称为质心，用质心对该簇进行描述。

K-means算法在P个样本中随机选取K个样本作为初始聚类中心点，而对于剩余的其他样本，根据与所选的各聚类中心点的相似度或者距离，将它们分别分配给相似度最高或者距离最近的类，然后计算每一类中样本数据的平均值，更新聚类中心点（质点），并不断重复这个过程，直到各个质心不再变化。

K-means算法中的关键步骤是计算样本与所有聚类中心的距离，生成新的聚类中心。

三、K-means聚类中K值的选择

K-means算法通常使用肘部法则来选择K值。肘部法则考察聚类后全体样本的误差平方和SSE，将SSE随K值的变化由快速下降转变为缓慢变化的拐点处的K值，作为最佳聚类簇数。

肘部法则选择K值的依据：随着聚类数K的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。且当K小于真实聚类数时，由于K的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大；当K达到真实聚类数时，再增加K所得到的聚合程度，回报就会迅速变小，所以SSE的下降幅度会骤减，然后随着K值的继续增大而趋于平缓。也就是说SSE与K之间的关系就像手肘的形状，这个肘部对应的K值就是数据的真实聚类数。

四、实例

1、使用KMeans()类对数据集iris进行聚类分析

加载iris数据集，按照4个特征，使用肘部法则确定最佳的K值，然后使用KMeans类进行聚类，最后可视化聚类结果。

# 对iris数据进行聚类
import numpy as np 
import matplotlib.pyplot as plt 
import pandas as pd 
from sklearn import datasets
# 导入数据集iris
iris=datasets.load_iris()
# 取样本数据的4列，作为特征属性
X=iris.data
y=iris.target
plt.rc('font',size=14)
plt.rcParams['font.sans-serif']='SimHei'
plt.rcParams['axes.unicode_minus']=False
# 计算K值从1到10对应的平均畸变程度，寻找最佳的K值
def DrawElbowKMeans(X):
    # 导入KMeans模块
    from sklearn.cluster import KMeans
    # 导入scipy,求解距离
    from scipy.spatial.distance import cdist
    K=range(1,10)
    meandistortions=[]
    for k in K:
        kmeans=KMeans(n_clusters=k)
        kmeans.fit(X)
        meandistortions.append(sum(np.min(cdist(X,kmeans.cluster_centers_,'euclidean'),axis=1))/X.shape[0])
    import matplotlib.pyplot as plt
    plt.grid(True)
    plt.plot(K,meandistortions,'kx-')
    plt.xlabel('k')
    plt.ylabel(u'平均畸变程度')
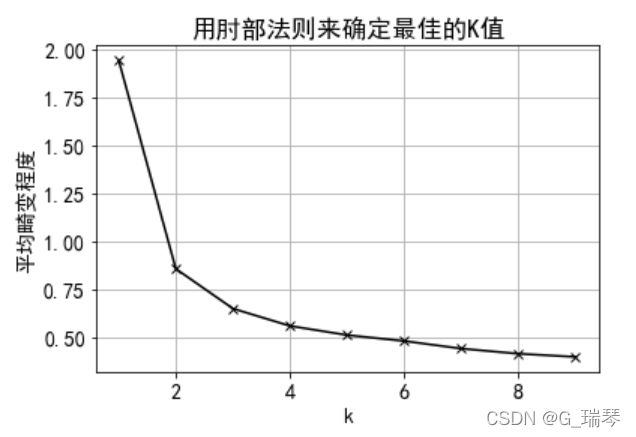
    plt.title(u'用肘部法则来确定最佳的K值')
DrawElbowKMeans(X=X)
plt.show() # 显示图形

 我们可以从图形中知道，较好的K值为2或3，

2、按照K=3对数据集进行极差标准化，拟合K均值聚类模型

from sklearn.preprocessing import MinMaxScaler 
from sklearn.cluster import KMeans
data=X
scale=MinMaxScaler().fit(data)
dataScale=scale.transform(data)
kmeans=KMeans(n_clusters=3).fit(dataScale)  # 构建并训练模型

3、可视化

# 可视化，观察聚类结果，与原始类别进行对比
labels=kmeans.labels_   # 提取聚类结果的类标签
plt.scatter(range(y.size),y,c='k',marker='.')
plt.scatter(range(y.size),labels+.1,c='k',marker='x')
plt.xlim((0,y.size))
plt.xlabel('样本序号')
plt.ylabel('分类/聚类标签')
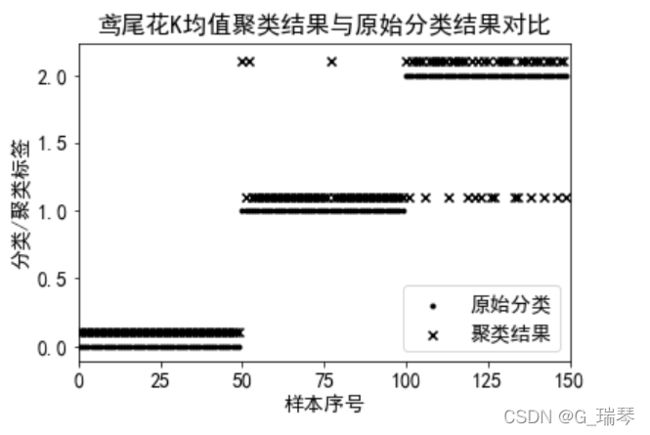
plt.title('鸢尾花K均值聚类结果与原始分类结果对比')
plt.legend(['原始分类','聚类结果'])
plt.show()

我们可以从可视化结果中得到：3个类别的类标签与各自聚类结果的簇标签是相同的，类0的聚类错误样本数为0个，类1的聚类错误样本数量为3个，类3的聚类错误样本数为14个。